matlab数据的获取、预处理、统计、可视化、降维 | 《matlab数学建模方法与实践（第三版）》学习笔记
目录
一、数据的获取
1.1 从Excel中获取
使用readtable()
使用xlsread()——xlswrite()
1.2 从TXT中获取
使用load()
使用textread()
使用fopen() fread() fclose()
使用fprintf()写入信息到txt
1.3 从图片中获取
使用imread
1.4 从视频获取
使用视觉工具箱中的VideoFileReader
二、数据的预处理
2.1 缺失值处理
2.2 噪声过滤
2.3 数据集成
2.4 数据归约
2.5 数据变换
1、标准化
2、离散化
3、语义转换
三、 数据的统计
3.1 基本描述性统计
1、表示位置的统计量：算数平均值（均值）、中位数
2、表示数据散度的统计量：标准差、方差、极差
3、表示分布形状的统计量：偏度和峰度
3.2 分布描述性统计
四、数据可视化
4.1 基本可视化
4.2 数据分布形状可视化
4.3 数据关联可视化
4.4 数据分组可视化
五、数据降维
数据的准备是数学建模的基础，主要介绍数据的获取、预处理、统计、可视化及降维。
一、数据的获取
1.1 从Excel中获取
使用readtable()
例1：使用spreadsheetImportOptions（Name,Value）初步确定导入信息，再用opts.Name=Value的格式添加。
% 工作簿: C:\Users\Hao\Desktop\程序_MATLAB数学建模方法与实践_卓金武等\Cha2\sz000004.xls
% 工作表: Sheet1
%% 设置导入选项并导入数据
opts = spreadsheetImportOptions("NumVariables", 8);%变量数8
%spreadsheetImportOptions允许指定 MATLAB® 如何从电子表格文件中导入表格数据
% 指定工作表和范围
opts.Sheet = "Sheet1";
opts.DataRange = "A1:H45";
% 指定列名称和类型
opts.VariableNames = ["Date", "DateNum", "Popen", "Phigh", "Plow", "Pclose", "Volum", "Turn"];
opts.VariableTypes = ["double", "double", "double", "double", "double", "double", "double", "double"];
% 导入数据
sz000004 = readtable("C:\Users\Hao\Desktop\程序_MATLAB数学建模方法与实践_卓金武等\Cha2\sz000004.xls", opts, "UseExcel", false);
%% 清除临时变量
clear opts例2：先初始化spreadsheetImportOptions对象，再用opts.Name=Value的格式逐个添加。
% 初始化 SpreadsheetImportOptions 对象
opts = spreadsheetImportOptions;
% 指定变量名称
opts.VariableNames = 'LastName';
% 变量类型
opts.VariableTypes = 'categorical';
% 数据起始单元格
opts.DataRange = 'A2';
% 使用导入选项预览文件中的八行数据
preview('patients.xls',opts)
oneVar = readtable('patients.xls',opts);
% 列出变量及大小和类型
whos oneVar例3：将导入信息存到变量里，再使用spreadsheetImportOptions（Name,Value）添加导入信息。
% 变量数
numVars = 7;
% 变量名称
varNames = {'LastName','Gender','Age','Location','Height','Weight','Smoker'} ;
% 变量类型
varTypes = {'char','categorical','int32','char','double','double','logical'} ;
% 数据起始单元格
dataStartLoc = 'A2';
% 使用 spreadsheetImportOptions 函数和变量信息初始化导入选项对象 opts
opts = spreadsheetImportOptions('NumVariables',numVars,...
'VariableNames',varNames,...
'VariableTypes',varTypes,...
'DataRange', dataStartLoc);
% 使用导入选项预览文件中的八行数据
preview('patients.xls',opts)
% 使用 readtable 导入数据
T = readtable('patients.xls',opts);
% 列出变量及大小和类型
whos T注：readtable 仅支持下列名称-值对组：
-
文本和电子表格参数 -
ReadVariableNames、ReadRowNames -
仅文本参数 -
DateLocale、Encoding -
仅电子表格参数 -
Sheet、UseExcel
使用xlsread()——xlswrite()
a=xlsread('C:\Coporation_evaluation.xlsx',2,'A2:I16')- 'C:\Coporation_evaluation.xlsx' 表示读入Excel数据所在位置
- 2 表示位于sheet2
- 'A2:I16' 表示读入的数据范围
a=xlswrite('C:\Coporation_evaluation.xlsx',a,3,'B1:C5')- 'C:\Coporation_evaluation.xlsx' 表示写入Excel工作簿所在位置，若不存在会自动创建
- a 表示待写入的数据
- 3 表示sheet3
- 'B1:C5' 表示写入Excel中的的具体位置
1.2 从TXT中获取
使用load()
% 生成线性间距向量，返回包含 1 和 30 之间的 8（默认100）个等间距点的行向量
a=linspace(1,30,8);
save d:\exper.txt a -ascii;
b=load('d:\exper.txt')- save d:\exper.txt a -ascii; 把a以ASCII码的形式存储在D盘的exper.txt中，若不存在会自动创建
- b=load('d:\exper.txt') 读取'd:\exper.txt'中的数据，并储存在变量b中
使用textread()
[A,B,C,...]=textread('filename','format',N,'headerlines',M)- filename 表示txt文件名称
- format 表示所读取变量的字段格式
- N 表示读取的次数
- headerlines 表示从第M+1行开始读取
[name,type,x,y,answer]=textread('D:t.txt','%s Type%d %f %n %s',2,...
'headerlines',1)
% 格式Type%d只显示%d,因为原数据为Type1,Type2,Type3,Type4使用fopen() fread() fclose()
例：读取.m文件中的字符（读取txt文件也可以）
% 用函数fopen打开文件，r代表只读形式打开，w代表写入形式打开，a代表在文件末尾添加内容
fid=fopen('D:\CRM4.m','r');
% 以字符形式读取整个文本
var=fread(fid,'*char');
% 将中文字段转换为相应的2字节代码，否则输出可能会乱码
var=native2unicode(var)
fclose(fid)使用fprintf()写入信息到txt
fprintf('file','format',a1，a2...)- file 表示文件路径
- format 表示数据写入类型
- a 表示要写入的数据内容
例：理解%m.nf数据类型
% 打开文件
file_h=fopen('C:\Users\Hao\Desktop\程序_MATLAB数学建模方法与实践_卓金武等\Cha3\math114.txt','w')
fprintf(file_h,'%6.2f %12.8f',3.14,2.718);
%宽度为6，不足左端空格补全，小数点后2位；宽度为12，不足左端空格补全，小数点后8位
%%6.2f %12.8f之间的空格也作数
%小数点也占位
fprintf(file_h,'\n%6f%12f',3.14,-2.718);
%小数点默认6位，实际宽度大于规定宽度6；宽度12，小数点默认6位
%负号也占位
fprintf(file_h,'\n%.2f%.8f',3.14,-2.718);
fclose(file_h)运行结果：
1.3 从图片中获取
使用imread
%% 读取图片
clc, clear, close all
a1=imread('000.bmp');
% 获得像素矩阵行数列数
[m,n]=size(a1);
%% 批量读取图片
dirname = 'ImageChips'; % 'ImageChips'文件夹
files = dir(fullfile(dirname, '*.bmp'));
%% fuiifile用法
% f = fullfile('myfolder','mysubfolder','myfile.m')
% f = 'myfolder/mysubfolder/myfile.m'
%% dir用法
% dir name 列出与 name 匹配的文件和文件夹。如果 name 为文件夹，dir 列出该文件夹的内容。使用绝对
% 或相对路径名称指定 name。name 参数的文件名可以包含 * 通配符，路径名称可以包含 * 和 ** 通配符。
% 与** 通配符相邻的字符必须为文件分隔符。
a=zeros(m,n,19); % 创建全零数组19个m*n数组，共19张图片
pic=[];
for ii = 1:length(files)
filename = fullfile(dirname, files(ii).name);
a(:,:,ii)=imread(filename); % 将该图片信息读取到a的第ii个数组里
pic=[pic,a(:,:,ii)]; % 拼接图像
end
double(pic);
figure
imshow(pic,[])
% imshow(I,[low high]) 显示灰度图像 I，以二元素向量 [low high] 形式指定显示范围
% 若为[]，使用 [min(I(:)) max(I(:))] 的显示范围。换句话说，I 中的最小值是黑色，最大值是白色1.4 从视频获取
使用视觉工具箱中的VideoFileReader
%% 读取视频数据
% 从视频文件中读取视频帧、图像和音频样本
videoFReader = vision.VideoFileReader('vippedtracking.mp4');
% 播放视频文件
videoPlayer = vision.VideoPlayer;
while ~isDone(videoFReader)
% 当来自有限数据源的数据取完时（通常是因为已读取所有数据），isDone(obj)返回true
% ~逻辑非
videoFrame = step(videoFReader); % 运行videoFReader算法，返回输出参数
step(videoPlayer, videoFrame); % 对videoFrame运行videoPlayer算法
end
release(videoPlayer); %释放资源
%% 设置播放方式
% 重置播放器
reset(videoFReader) % 将图形对象属性重置为其默认值
% 增加播放器的尺寸
r = groot; % r = groot 用于存储图形根对象的句柄。要使用圆点表示法设置根属性，首先必须存储句柄
scrPos = r.ScreenSize;
% Size/position is always a 4-element vector: [x0 y0 dx dy]
dx = scrPos(3); dy = scrPos(4);
videoPlayer = vision.VideoPlayer('Position',[dx/8, dy/8, dx*(3/4), dy*(3/4)]);
% 指定左下角和右上角的坐标
while ~isDone(videoFReader)
videoFrame = step(videoFReader);
step(videoPlayer, videoFrame);
end
release(videoPlayer);
reset(videoFReader)
%% 获取视频中的图像
videoFrame = step(videoFReader);
n = 0;
while n~=15
videoFrame = step(videoFReader);
n = n+1;
end
figure, imshow(videoFrame) % 获得第15张图像
release(videoPlayer);二、数据的预处理
数据质量三要素：准确性、完整性、一致性（格式不一致等）
两个影响因素：可信性（多少是用户信赖的）、可解释性 （是否容易理解）
2.1 缺失值处理
1、删除法
2、插补法（以最可能的值来插补缺失值）
均值插补：定距型用平均值，不定距型用众数，分布规律规范用中值
回归插补：利用线性或非线性回归技术
极大似然估计：当缺失类型为随机缺失，通过观测数据边际分布对未知参数进行估计
2.2 噪声过滤
1、回归法
用一个函数拟合数据来光滑数据，通常先对数据进行可视化，判断数据趋势及规律，再确定是否可以用回归法去噪。
2、均值平滑法
对于具有序列特征的变量用邻近的若干数据的均值来替换原始数据的方法。
3、利群点分析法
通过聚类等方法来检测离群点，并将其删除。
4、小波过滤法（小波去噪）
本质是一个函数逼近问题，即寻找从实际信号空间到小波函数空间的最佳映射。
2.3 数据集成
将若干个分散的数据源中的数据，逻辑地或物理地集成到一个统一的数据集合中。
对于数据表的集成，主要有内接（理解为交集）和外接（理解为并集）两种方式。
2.4 数据归约
目的是得到能够与原始数据集近似等效甚至比其更好但数据量却较少的数据集。
2.5 数据变换
将数据从一种表示形式变为另一种表现形式的过程。
1、标准化
将数据按比例缩放，使之落入一个小的特定区间。便于不同单位或量级的指标能够进行比较和加权。
（1）0-1标准化（离差标准化）
当有数据加入时，需要重新定义。
（2）z标准化（标准差标准化）
经过处理的数据符合标准正态分布。
2、离散化
指把连续型数据切分成若干“段”，也称bin。
作用：算法需要；有效克服数据中隐藏的缺陷，使模型结果更加稳定；有利于对非线性关系进行诊断和描述。
3、语义转换
如：用｛1 2 3 4｝代替｛非常好 好 一般 差｝。
三、 数据的统计
概念：总体、个体、样本、样本容量
任务：由样本推断总体
3.1 基本描述性统计
1、表示位置的统计量：算数平均值（均值）、中位数
mean(x)返回均值，median(x)返回中位数
2、表示数据散度的统计量：标准差、方差、极差
标准差：
![s=[\frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}]^{\frac{1}{2}}](http://img.e-com-net.com/image/info8/8e9299fce0a743dbb5420fb40ef619ba.gif)
注：上式为样本标准差公式，n-1是为了满足无偏估计的要求，总体标准差公式n-1换为n。
方差：标准差的平方。
极差：最大值与最小值之差。
3、表示分布形状的统计量：偏度和峰度
偏度：反映分布的对称性，
>0为右偏态，此时右边数据比左边数据多，<0左偏态，情况相反，接近0，分布对称。
峰度：正态分布峰度为3，若
比3大得多，表示样本中有较多远离均值的数据。
skewness(x)返回偏度，kurtosis(x)返回峰度
3.2 分布描述性统计
- 随机变量的特性完全由其（概率）分布函数或密度函数来描述。
- 分位数：对于0<
<1，使某分布函数F(x)=的x成为这个分布的的分位数，记作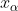
。 - 直方图可以看作密度函数图形的（离散化）近似。
四、数据可视化
4.1 基本可视化
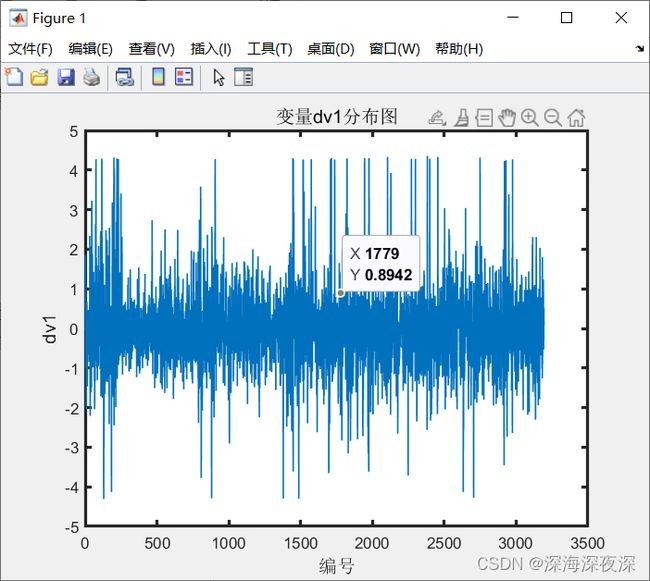
先用最基本的绘图命令plot绘制各变量分布趋势。
代码如下：
% 数据可视化——基本绘图
% 读取数据
clc, clear al, close all
X=xlsread('dataTableA2.xlsx');
% 绘制变量dv1的基本分布
N=size(X,1); % 返回X第1个维度的长度
id=1:N;
figure
plot( id', X(:,2),'LineWidth',1) % 表示 id'的转置矩阵
set(gca,'linewidth',2);
% set(H,Name,Value) 为 H 标识的对象指定其 Name 属性的值
% gca表示当前坐标范围，即设置图框的线宽
xlabel('编号','fontsize',12); % 'fontsize'为设置字体大小
ylabel('dv1', 'fontsize',12);
title('变量dv1分布图','fontsize',12);运行结果：
4.2 数据分布形状可视化
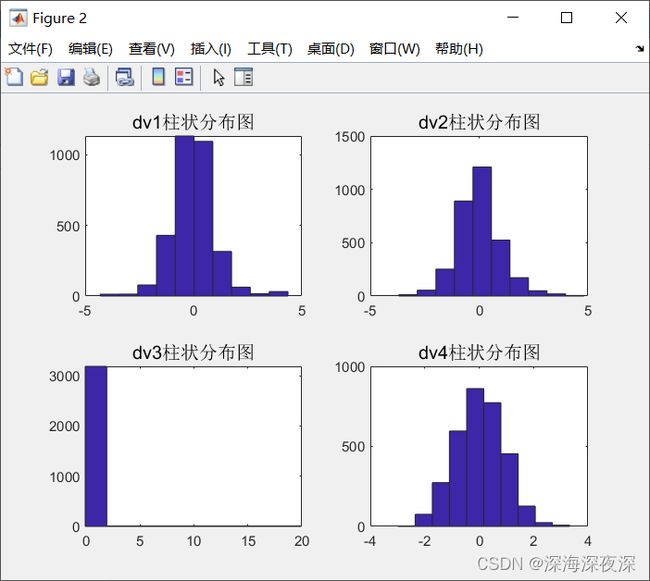
分析数据分布特征，绘制柱状分布图。
代码如下：
% 同时绘制变量dv1-dv4的柱状分布图
figure
subplot(2,2,1);
% 在当前窗划分2*2网格，1代表第一行第一列，2第一行第二列，3第二行第一列...
hist(X(:,2)); % 绘制直方图，建议使用histogram
title('dv1柱状分布图','fontsize',12)
subplot(2,2,2);
hist(X(:,3));
title('dv2柱状分布图','fontsize',12)
subplot(2,2,3);
hist(X(:,4));
title('dv3柱状分布图','fontsize',12)
subplot(2,2,4);
hist(X(:,5));
title('dv4柱状分布图','fontsize',12)运行结果：
下面将常用的统计量绘制在分布图中。
代码如下：
% 数据可视化——数据分布形状图
% 读取数据
clc, clear al, close all
X=xlsread('dataTableA2.xlsx');
dv1=X(:,2);
% 绘制变量dv1的柱状分布图
h = -5:0.5:5;
n=hist(dv1,h); % 得到包含20个元素的列表，表示频数
figure
bar(h, n) % 绘制条形图
%相当于将小于-5和大于5的少量数据舍去
% 计算常用的形状度量指标
mn = mean(dv1); % 均值
sdev = std(dv1); % 标准差
mdsprd = iqr(dv1); % 四分位数Q=Q3-Q1
mnad = mad(dv1); % 中位数
rng = range(dv1); % 极差
% 标识度量数值
x = round(quantile(dv1,[0.25,0.5,0.75])); % 四分位数3个点
% quantile返回分位数，round（x,n）四舍五入，n表示圆整几位，若n为负数，向右补零
y = (n(h==x(1)) + n(h==x(3)))/2; % (Q1对应频数+Q3对应频数)/2
line(x,[y,y,y],'marker','x','color','r') % 绘制线条
x = round(mn + sdev*[-1,0,1]); % 均值加减标准差
y = (n(h==x(1)) + n(h==x(3)))/2; % （均值加标准差对应频数+均值减标准差对应频数）/2
line(x,[y,y,y],'marker','o','color',[0 0.5 0])
x = round(mn + mnad*[-1,0,1]); % 均值加减中位数
y = (n(h==x(1)) + n(h==x(3)))/2;
line(x,[y,y,y],'marker','*','color',[0.75 0 0.75])
x = round([min(dv1),max(dv1)]); % 最小值，最大值
line(x,[1,1],'marker','.','color',[0 0.75 0.75])
legend('Data','Midspread','Std Dev','Mean Abs Dev','Range')
% 在坐标区绘制图例运行结果：
4.3 数据关联可视化
数据关联可视化对分析哪些变量更有效具有更直观的效果，数据筛选前可以先利用关联可视化了解各变量间的关联关系。
代码如下：
% 数据可视化——变量想相关性
% 读取数据
clc, clear al, close all
X=xlsread('dataTableA2.xlsx');
Vars = X(:,7:12);
% 绘制变量间相关性关联图
figure
plotmatrix(Vars) % 散点图矩阵
% plotmatrix(X,Y) 创建一个子坐标区矩阵，包含了由 X 的各列相对 Y 的各列数据组成。
% 的散点图如果 X 是 p*n 且Y是 p×m，则plotmatrix生成一个n*m子坐标区矩阵。
% plotmatrix(X)与plotmatrix(X,X) 相同。除了用 histogram(X(:,i)) 替换了第i列
% 中对角线上的子坐标区。
% 绘制变量间相关性强度图
covmat = corrcoef(Vars);
% R = corrcoef(A) 返回A的相关系数的矩阵，其中A的列表示随机变量，行表示观测值。
% R = corrcoef(A,B) 返回两个随机变量A和B之间的系数。
figure
imagesc(covmat);
% imagesc(C) 将数组 C 中的数据显示为一个图像，该图像使用颜色图中的全部颜色
grid; % 显示/隐藏坐标区网格线
colorbar; % 显示色阶颜色栏运行结果：
4.4 数据分组可视化
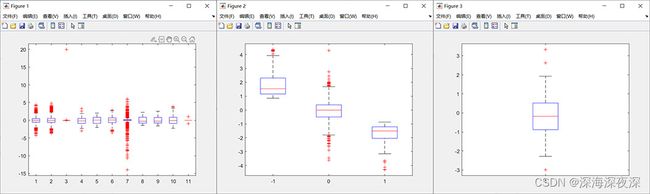
按照不同的分位数将数据进行分组，典型的图形是箱体图，根据箱体图可以看出数据的分布特征和异常值的数量。
代码如下：
% 数据可视化——数据分组
% 读取数据
clc, clear al, close all
X=xlsread('dataTableA2.xlsx');
dv1=X(:,2);
eva=X(:,12);
% Boxplot，绘制箱体图
% boxplot(x) 创建x中数据的箱线图。如果x是向量，boxplot绘制一个箱子。
% 如果x是矩阵，boxplot为x的每列绘制一个箱子。
% 在每个箱子上，中心标记表示中位数，箱子的底边和顶边分别表示第25个和75个百
% 分位数。须线会延伸到不是离群值的最远端数据点，离群值会以 '+' 符号单独绘制。
% boxplot(x,g) 使用g中包含的一个或多个分组变量创建箱线图。boxplot为具有相同
% 的一个或多个g值的各组x值创建一个单独的箱子
figure
boxplot(X(:,2:12))
figure
boxplot(dv1, eva)
figure
boxplot(X(:,5))
运行结果：
五、数据降维
主成分分析（PCA）基本原理：
将原来众多具有一定相关性的变量，重新组合为一组新的相互无关的综合变量来代替原来的变量
PCA方法步骤：
- 对原始数据进行标准化处理
- 计算样本相关系数矩阵
- 计算相关系数矩阵的特征值和相应的特征向量
- 选择重要的主成分，并写出主成分表达式（贡献率）
- 计算主成分得分
- 依据主成分得分的数据进一步分析和建模