【数据分析】基于FCM进行交通数据聚类分析matlab源码

事物间的界线，有些是明确的，有些则是模糊的。当聚类涉及到事物之间的模糊界线时，需要运用模糊聚类分析方法。
如何理解模糊聚类的“模糊”呢：假设有两个集合分别是A、B，有一成员a，传统的分类概念a要么属于A要么属于B，在模糊聚类的概念中a可以0.3属于A，0.7属于B，这就是其中的“模糊”概念。

模糊聚类分析有两种基本方法：系统聚类法和逐步聚类法。

系统聚类法个人理解类似于密度聚类算法，逐步聚类法类是中心点聚类法。（这里有不对的地方请指正）

逐步聚类法是一种基于模糊划分的模糊聚类分析法。它是预先确定好待分类的样本应分成几类，然后按照最优原则进行在分类，经多次迭代直到分类比较合理为止。在分类过程中可认为某个样本以某一隶属度隶属某一类，又以某一隶属度隶属于另一类。这样，样本就不是明确的属于或不属于某一类。若样本集有n个样本要分成c类，则他的模糊划分矩阵为c×n。
该矩阵有如下特性：
①. 每一样本属于各类的隶属度之和为1。
②. 每一类模糊子集都不是空集。

模糊C-means聚类算法

模糊c-均值聚类算法fuzzy c-means (FCM)。在众多模糊聚类算法中，模糊C-均值(FCM)算法应用最广泛且成功，它通过优化目标函数得到每个样本点对所有类中心的隶属度，从而对样本进行自动分类。

FCM算法原理

假定我们有数据集X，我们要对X中的数据进行分类，如果把这些数据划分成c个类的话，那么对应的就有c个类中心为Ci，每个样本Xj属于某一类Ci的隶属度定为Uij，那么定义一个FCM目标函数及其约束条件如下：

目标函数(式1)由相应样本的隶属度与该样本到各类中心的距离相乘组成的，式2为约束条件，也就是一个样本属于所有类的隶属度之和要为 1 。
式1中的m是一个隶属度的因子，一般为2 ，||Xj - Ci|| 表示Xj到中心点Ci的欧式距离。

目标函数J越小越好，说以我们要求得目标函数J的极小值，这里如何求极小值就不推导了（对推导感兴趣的可以看这篇文章：https://blog.csdn.net/on2way/article/details/47087201），直接给出结论：

Uij的迭代公式：

Ci的迭代公式：

我们发现Uij和Ci是相互关联的，彼此包含对方，那么问题来了，fcm算法开始的时候既没有Uij也没有Ci，那么如何求解呢？很简单，程序一开始的时候我们会随机生成一个Uij，只要数值满足条件即可，然后开始迭代，通过Uij计算出Ci，有了Ci又可以计算出Uij，反反复复，这个过程中目标函数J一直在变化，逐渐绉向稳定。那么当J不在变化时就认为算法收敛到一个较好的结果了。

clear 
clc
% 注释中前面带数字的地方是您可能需要改的地方。
xls_name = '实验数据汇总.xls';  % 1.要读取的Excel表格的名字
%df = xlsread(xls_name);
[df,date]=xlsread(xls_name);
%data = df(:,2:4);
data=df(:,1:3);
plot3(data(:,1),data(:,2),data(:,3),'o');hold on;
%% 时间处理
%time = df(:,1)';
%date=cell2mat(date)
%time=date{3,1};
time=1:609;
%% 聚类处理
% 加权重在这一部分
% weight = [1.5,3,2]; % 2.权重向量，因为您的数据有三列，所以权重向量有三个分量,1.5,1,1
% [U,V,objFun] = myfcm(weight, data, 3); % 3.这条语句括号中的4设置聚成4类，改成3则聚为3类。
options=[3,20,1e-6,0];
cn=4;
X=data;
[center,U,obj_fcn]=fcm(X,cn,options);
Jb=obj_fcn(end);
maxU = max(U);
index1 = find(U(1,:) == maxU);
index2 = find(U(2, :) == maxU);
index3 = find(U(3, :) == maxU);
%% 分类情况
% 在前三类样本数据中分别画上不同记号 不加记号的就是第四类了
plot3(X(index1,1), X(index1, 2), X(index1, 3), 'linestyle', 'none', 'marker', 'x', 'color', 'g'); hold on; 
plot3(X(index2,1), X(index2, 2), X(index2, 3), 'linestyle', 'none', 'marker', '*', 'color', 'r'); hold on;
plot3(X(index3,1), X(index3, 2), X(index3, 3), 'linestyle', 'none', 'marker', '+', 'color', 'b'); hold on;
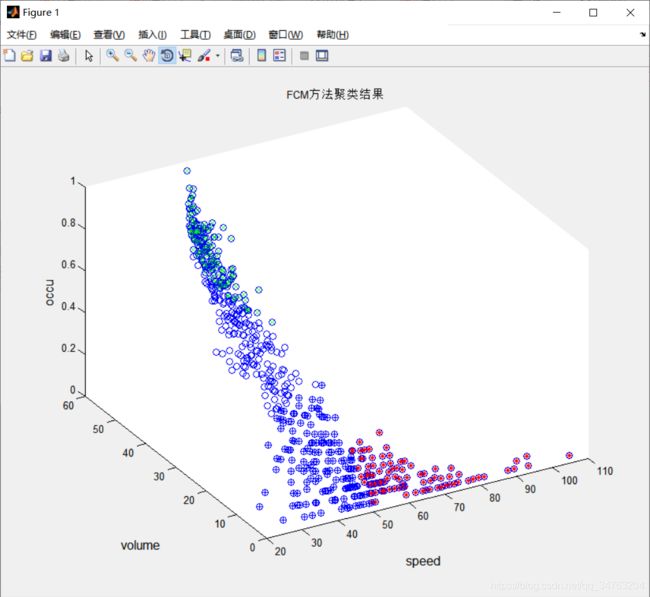
xlabel('speed','fontsize',12);
ylabel('volume','fontsize',12);
zlabel('occu','fontsize',12);
title('FCM方法聚类结果');