吴恩达机器学习总结（二）——Logistic回归和简单的神经网络（附作业）

在线性回归模型中，输入和输出一般都是连续的，对于每个输入x，都有一个对应的输出y，模型的定义域和值域都可以是$(-\infty ,+\infty )$。而对于分类模型来说，其输入可以是连续的，但它的输出是离散的，即只有有限个输出y。例如，其值域可以只有两个值{0, 1}，这两个值可以表示对样本的某种分类，高/低、患病/健康、阴性/阳性等，这就是最常见的二分类问题。

二、Logistic回归

逻辑回归带有回归二字，但它是一个分类算法。Logistics回归的函数为：
$$g(z)=\frac{1}{1+e^{-z}}$$
其定义域为全体实数，值域为[0,1]。其函数图像如图：

当x的值很大（或很小）时，y的值接近1或0，这时可以认为这是一个0或1的二分类的问题。我们选择一个阈值，通常为0.5（在癌症分类这种问题中，可以适当提高阈值，确保我们有高置信度认为癌/健康），当y>0.5时，归为1类；当y<0.5时，归为0类。
我们利用线性回归的办法来拟合，将$z$替换为${\theta }^{T}X$，得到Logistics回归模型如下：$$h_{\theta }(x)=g({\theta }^{T}X)=\frac{1}{1+e^{-{\theta }^{T}X}}$$
$P(y=1|x;\theta )=h_{\theta }(x)$，$P(y=0|x;\theta )=1-h_{\theta }(x)$。以癌症肿瘤分类为例，0为良性，1为恶性肿瘤，若$h_{\theta }(x)=0.7$就可以表述成，有70%的概率认为是恶性肿瘤。

1.代价函数

我们记预测值$h_{\theta }(x)$与真实值y之间的差异的函数为代价函数$Cost(h_{\theta }(x^{(i)}),y^{(i)})$，所有样本代价函数的均值为：
在逻辑回归函数中，我们不采用均方误差作为代价函数，而是采用下图所示的代价函数：

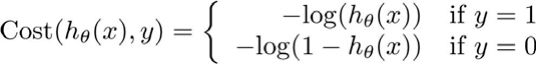
其示意图如下：

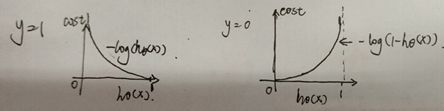
将代价函数简化以后：
$$Cost(h_{\theta }(x),y)=-ylog(h_{\theta }(x))-(1-y)log(1-h_{\theta }(x))$$
所有样本点的平均代价函数为：
$$J(\theta )=-\frac{1}{m}[\sum _{i=1}^m(y^{(i)}\log h_{\theta }(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))]$$

2.梯度下降

我们的步骤和线性回归时一样，要找到一个$\theta$，使得$minimizeJ(\theta )$，还是采用梯度下降的方法。

求导得出：

其中，$\alpha$为步长，也称学习率。

3.正则化

这里我想引入一个正则化的概念，当我们用模型去拟合数据时，若数据的特征过多，会产生过拟合的情况，即模型对现有数据都拟合的很好，而当输入新的数据时，拟合的效果却不尽人意。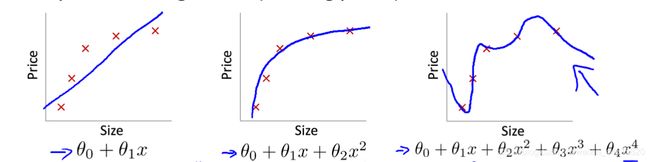
最右图就是模型过拟合的表现。
为了避免过拟合，可以通过减少特征（手动删除或选择特征数少的模型）或正则化（保留所有特征，但减小参数$\theta$的值），往往正则化对多特征的数据效果很好。
因此，正则化的目的就是尽可能的让所有$\theta$越小。我们加入正则化项来改写代价函数$J(\theta )$。
正则化Logistics回归模型为：
$$J(\theta )=-\frac{1}{m}[\sum _{i=1}^m(y^{(i)}\log h_{\theta }(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2]$$
对其参数$\theta$：
$${\theta }_j:={\theta }_j-\alpha [\frac{1}{m}(h_{\theta }(x^{(i)}-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{\theta }_j]$$
一般我们都才用正则化后的模型去拟合数据，来避免过拟合。

4.多分类

前述均为二分类的情况，分为0和1两类。当遇到多分类的情况时，也可以运用二分类的思维去处理。
‘OvO’：One vs. One，即一对一。将多分类的类别两两配对，从而产生$\frac{N(N-1)}{2}$个分类任务。在对新数据集进行分类时，将产生$\frac{N(N-1)}{2}$个分类结果，然后对分类结果进行投票，对预测结果中投票最多的结果作为最终的分类结果。
‘OvR’：One vs. Rest，一对其余。OvR的主要思路是，将一个类认为是‘+’，剩下的类都为‘-’，有N个类，所以能训练产生N个分类器。在测试时，若仅有一个类别为‘+’，则该类别为最终的分类结果；若有多个结果都为‘+’，则需要考虑各个‘+’分类器的置信度，置信度最高的为最终的分类结果。
‘MvM’：Many vs. Many，多对多。选择若干分类器为‘+’，若干为‘-’，常用ECOC（纠错输出码）的方法来判断最终的输出结果。

---

以课后作业EX3为例
目的识别手写数字图像，数字图像有0,1,2…9共10个类别，共5000个样本，20x20个像素，也就是400个特征。
随机选择100个图像可视化

import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt
import seaborn as sns 
import os 
import os.path
from scipy.io import loadmat
from sklearn.metrics import classification_report#这个包是评价报告

data=loadmat("C://Users//HP//ANG_Homework//ex3-neural network//ex3data1.mat")
X=data['X']
y=data['y']

#定义随机展示一张图像的函数
def display_one_Data(X):
    #随机选择一个图像
    random_number=np.random.randint(0,5000)
    random_data=X[random_number,:]
    #可视化
    fig,ax=plt.subplots(figsize=(1,1))
    ax.matshow(random_data.reshape(20,20).T,cmap='gray_r') #不加.T的话，数字是反的
    #去除刻度
    plt.xticks([])
    plt.yticks([])
    plt.show()
    
#同可视化一个的过程，同时可视化100个
def display_100_data(X):
    random_number=np.random.choice(range(0,5000), 100)
    random_data=X[random_number,:]
    fig,ax_array=plt.subplots(nrows=10,ncols=10,sharey=True, sharex=True,figsize=(6,6)) #sharey ,sharex表示是否公用一个坐标轴,默认False
    for r in range (10):
        for c in range(10):
            ax_array[r,c].matshow(random_data[r*10+c].reshape(20,20).T,cmap='gray_r')
            plt.xticks([])
            plt.yticks([])
    plt.show()

display_100_data(X)
#subplots()可以一次生成多个，在调用时只需要调用生成对象的ax即可
#fig，ax = subplots(nrows,ncols,sharex,sharey,squeeze,subplot_kw,gridspec_kw,**fig_kw)  创建画布和子图

输出如下：

接着尝试构建分类模型

#向量化Logistic回归
#定义sigmoid函数
def sigmoid(z):
    return 1/(1+np.exp(-z))
    
#定义代价函数
def costfunction( X, y,theta):
    J_theta = -y.dot(np.log(sigmoid([email protected]))) - (y-1)。dot(np.log(1-sigmoid([email protected])))
    return np.mean(J_theta)

#定义正则化代价函数
def reg_costfunction(theta,X,y,l):
    m=X.shape[0]
    first=(-y).dot(np.log(sigmoid(X.dot(theta))))
    second=(-1+y).dot(np.log(1-sigmoid(X.dot(theta))))
    J_theta=(first+second)/m
    #reg是从j=1开始的
    theta_reg=theta[1:]
    reg=(l /(2*m)) * np.power(theta_reg, 2).sum()
    #reg = (l/2*len(X)) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))
    J=J_theta+reg
    return J
    
#定义梯度
def gradient(X,y,theta):
    grad=(sigmoid(X.dot(theta)-y)).T.dot(X/len(X))
    return grad

#定义正则化梯度下降
def reg_gradient(theta,X,y,l):
    theta_reg=theta[1:]
    first = (1/len(X))*X.T@(sigmoid(X@theta)-y)
    reg = np.concatenate([np.array([0]), (1/ len(X)) * theta_reg])
    return first+reg
    
#使用one-vs-all(一对多)logistic回归模型来构建一个多类分类器。由于有10个类，需要训练10个独立的分类器。

def one_vs_all(X,y,l,k):
#生成theta矩阵，其中每一行代表一个数字的theta向量（401维），一共10个数字，所以一共10行
    all_theta=np.zeros((k,X.shape[1])) #一个10x401维矩阵
    #print(all_theta.shape)
    for i in range(1,k+1):
        #获取每一个手写数字的y向量
        y_i=np.array([1 if num==i else 0 for num in y])
        #逐个训练theta向量
        theta_i=all_theta[i-1]
         #因为数字是从1开始，但索引是从0开始。
        #print(">>>>>>minimize<<<<<",X.shape,y_i.shape,theta_i.shape)
        result=minimize(fun=reg_costfunction,
                        x0=theta_i,
                        args=(X, y_i, l),
                        method='TNC',
                        jac=reg_gradient)
        #合并theta向量
        all_theta[i-1]=result.x
    return all_theta

def predict(theta,X):
    h = sigmoid(X.dot(theta.T))
    h_max=np.argmax(h,axis=1)  # 获取h每一行的最大值元素下标
    # 因为下标从0开始，所以加1
    h_max=h_max+1
    print(h_max.shape)  # (5000,)
    return h_max
    #return (h >= 0.5).astype(int)


data=loadmat("C://Users//HP//ANG_Homework//ex3-neural network//ex3data1.mat")
X=data['X']
X = np.insert(X,0,values=np.ones(X.shape[0]), axis=1)
y=data['y'].ravel()  # 降维，方便之后计算
#print(X.shape,y.shape)
all_theta=one_vs_all(X,y,1,10)
#print(all_theta)
y_predict=predict(all_theta,X)
#print(y_predict)
report=classification_report(y_predict,y)
print(report)
print(accuracy_score(y_predict,y))

输出如下：

---

三、神经网络

1.简介

受人脑启发，神经网络在早些年就已经出现了，随着如今算力的提高，又重回了人们的视野。如今，神经网络已成为人工智能领域最强大的算法之一。
上文所提到的Logistics回归，仅仅是一个线性分类器，有时候一个分类器是不足以解决问题的。例如XOR函数，这是一种布尔函数，只有在A和B仅有一个为真但两个输入不同时为真的情况下，才输出为真。如下表：


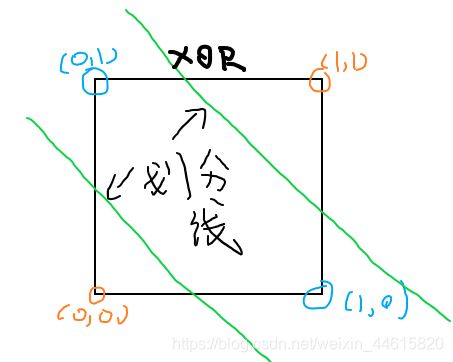
对于XOR函数，使用两个线性分类器一起工作，就能解决这个问题了。
使用多个分类器一起工作，这就是神经网络的核心思想。
在人体中，神经元能够通过树突接收电信号（或化学信号），然后将这些信号沿着轴突传递到突触，突触再将这些信号传递给其他神经元（或转化为化学信号）。这种输入-整合-输出的方式似乎和我们处理数据方式有些类似，所以人们据此创造了神经网络

但是，这些传入的信号也是有强有弱的，所以我们为每个信号都赋予一个权重W（参数），较小的权重将弱化信号，较大的权重将放大信号。随着神经网络学习过程的进行，神经网络可以通过调整优化网络内部的链接权重改进输出，使得输出值和真实值更加接近（有可能过拟合）。一般神经网络分为三大层，分别为输入层、隐藏层、输出层，每层的神经元个数没有固定的要求，需要人为的根据模型的预测结果调整和设置。

如上图，蓝色的W，就是权重参数，Z1神经元接收了来自上一层a1,a2,a3传递来的信号，这些信号分别被对应的权重w1,w2,w3修饰，Z1通过某个函数整合这些信号（相当于神经元的作用）然后在输出到下一个神经元，表示为公式就是$z_1=g(a_1\ast w_1+a_2\ast w_2+a_3\ast w_3)$，当然这只是一个简单的示意，在许多大型神经网络中，参数不仅只有一个w。

前馈

前馈神经网络是人工神经网络的一种，可以用于处理复杂的非线性分类情况。在此之中，各神经元从输入层开始，接收前一级输入，并输出到下一级，直至输出层。在这个神经网络中，各层无反馈。相比于线性回归、logistic回归，提高灵活性的同时，又不太会有过拟合、组合爆炸的情况。

这里使用一个前馈神经网络对上面那些手写数字的数据集进行分类，看看神经网络和Logistics回归之间的效果。

---

import numpy as np
import pandas as pd 
from scipy.io import loadmat
from sklearn.metrics import classification_report#这个包是评价报告
from sklearn.metrics import accuracy_score

def sigmoid(z):
    return 1/(1+np.exp(-z))

data=loadmat("C://Users//HP//ANG_Homework//ex3-neural network//ex3data1.mat")
X=data['X']
y=data['y'].ravel()
X = np.insert(X,0,1,axis=1)

a1=X
z2=a1.dot(theta1.T)
#z2.shape (5000, 25)
z2=np.insert(z2,0,1,axis=1)
#z2.shape(5000,26)

a2=sigmoid(z2)
#a2.shape
z3=a2.dot(theta2.T)
a3=sigmoid(z3)
#a3.shape
y_predict = np.argmax(a3, axis=1) + 1 
accuracy = np.mean(y_predict == y)
report=classification_report(y_predict,y)
print(report)
print("Accurancy:",accuracy_score(y_predict,y))

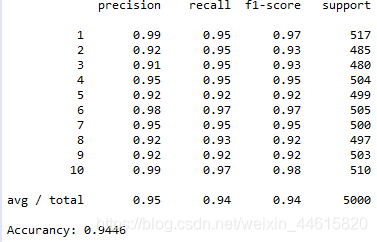
输出结果如下：

可以看出使用是神经网络以后，各项指数相比于多分类器的Logistics回归有所提高，说明在该数据集中，因为样本和特征数较多，使用神经网络的效果要好。
不过这里的参数theta，是课程作业上已经给出了的。