【人工智能】手掌相关信息测量【实验报告与全部代码】(QDU)
写在前面,防止有傻乎乎的同学直接全文复制出现问题。
实现的比较基础,基本都是图像处理的知识或者说是巧办法而不是很有说服力的方法;
一定要注意,QDU的张维忠老师会把上一届的实验报告给你们小组,所以如果是QDU的,复制这篇文章是没有用的,自己操作一下吧;
没有实现老师要求的手掌厚度测量,如果有能力的同学可以尝试一下三维重建等高级方法。
目录
一、实验背景
二、实验任务
三、任务分配
四、实验环境
五、实验思路
六、实验内容
1. MediaPipe Hands介绍
1.1 手部检测器
1.2 手部坐标预测模型
2. 裁剪手掌部分
2.1 确定手掌的倾斜角度
2.2 确定完整手掌所在区域
2.3 裁剪手掌区域
2.4 手掌边缘提取和获取手掌掩模图
3. 手掌各个部位像素长度的测量
3.1 手掌宽度
3.2 手腕宽度
3.3 手指宽度
3.4 手指长度
3.5 虎口角度
4. 像素长度转换为实际长度
4.1 霍夫圆检测
4.2 测距原理
4.3 检测掌心参考圆效果
七、效果展示
八、参考资料
九、全部代码
一、实验背景
手掌检测,是手套等用品生产商为了给客户更为精细的定制化需求而急需的计算机视觉技术。通过手机摄像头采集含有手掌的图像或视频流,并自动在图像中检测和跟踪手掌,进而对检测到的手掌进行手部的一系列相关技术。因为手套的舒适度与手套大小规格是否与人的手掌相契合有着密切的关系,因此对手掌视觉测量的精度提出很高的要求,手掌的视觉测量的难点如下:
1、特征过多:因为手掌纹路较多,因此难以对手掌整体轮廓进行非常精准的描绘。
2、误差难以消除:手掌长度通过参照物来确定,因为参照物会随着视觉变化而产生不可避免的形变,因此在长度单位映射时存在不可避免的误差。
二、实验任务
利用摄像头动态识别并捕捉手掌,精确测量手掌上五根手指的长度与宽度、关节的位置、手掌虎口的角度、手掌的宽度以及手腕的宽度。完成对手掌各个参数的精确测量,不断完善、提高参数计算精度。
三、任务分配
- 组长:负责手掌识别、手掌关键点定位、手掌图像预处理和手掌虎口角度测量
- 小组1:负责提取手掌掩模图和手掌边缘
- 小组2:负责测量手掌宽度和手腕宽度
- 小组3:负责测量手指长度和手指宽度
四、实验环境
- Window 10
- Python 3.6.15
- Anaconda3-2020.11-Windows-x86_64
- MediaPipe
- numpy 1.19.3
- scikit-learn 0.24.2
- opencv 4.5.3
- opencv-python 4.6.0.66
- opencv-contrib-python 4.6.0.66
五、实验思路
利用Google研发的MediaPipe Hands进行手掌识别和关键点定位。利用中指关键点和掌心关键点计算手掌倾斜角度,通过图像旋转保证手掌在图像中始终保持竖直,同时对于显示比较小的手掌(距离摄像头较远),通过图像放缩将图像放大至合适大小,以方便后续手掌的测量并减少膨胀、腐蚀等图像处理操作对长度信息的影响,保证测量的准确性。
将手掌的色彩空间从RGB转换到YCrCb提取手掌掩模图和手掌边缘,YCrCb类似于HSV,更适合描述人观察到的色彩世界。采用高斯滤波进行平滑处理后,利用YCrCb颜色空间的Cr分量和Otsu法阈值分割算法对图像进行二值化,从而获取手掌的掩模图。该算法考虑到图像由前景色和背景色组成,通过统计学的方法来选取一个能够将前景色和背景色尽可能的分开阈值。Otsu算法中利用最大类间方差来判断并选取最合适的阈值。对比基于RGB颜色空间的肤色检测模型、椭圆肤色检测模型、基于HSV颜色空间的肤色检测模型等模型后,YCrCb颜色空间的Cr分量+Otsu法阈值分割算法效果最佳。但是在手指位置光照强烈的情况下,手指部分会出现无法获取的问题。暂时的解决方案是考虑到尽管光照非常强,但在RGB色彩空间上R、G、B仍然满足一定的大小关系,因此将两种方法获取的掩模图合并,保证手指不存在缺少。但是实践表明效果在该特殊情况下确实有效,但其他比较理想的情况下反而会出现噪声的问题,效果不如直接在YCrCb色彩空间直接处理。
对于摄像头捕捉到的手掌,需要保证掌心位置存在已知实际半径长度的参照圆,利用霍夫圆检测获取参照圆的像素半径,采用一定的算法测量手掌各个部分的像素长度,根据摄像头单目测距的原理计算出对应的实际长度。
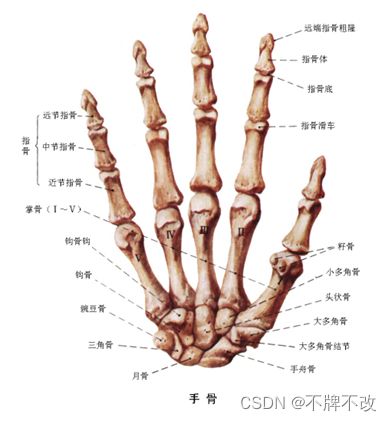
手指宽度测量的初步思想是在每根手指的对称位置多次取边缘点,通过残差分析去除偏离较大的离散点,对于剩下的点计算对应的距离取均值作为测量的像素长度。以测量中指宽度为例,可以分别在远节指骨、中节指骨,近节指骨(见图1)宽度方向上取三对点,对于中指每一侧的九个点(见图2),通过残差分析将阈值之外的离散点排除,对于同一侧剩下的点计算x坐标均值作为中指该侧的x坐标。另一侧同理,得到的两个x坐标之差为中指像素宽度。
对于手掌不同部分位置的确定,需要根据手掌不同部分的特点设计专门的算法确定位置。
图 1
图 2
后续在实现过程中发现残差分析无法有效地适用于获取的边缘图像素点坐标,因此抛弃了残差分析的思想。根据每根手指上的骨骼点计算出手指的倾斜程度,对手掌进行相应的旋转以保证手指竖直,同时将手指移至窗口中心位置,裁剪出每根手指所在区域。采用竖直方向投影的方式,计算像素累积值,根据设定的阈值确定手指宽度。对于非大拇指的四根手指的长度,将四个相邻骨骼点的距离之和作为对应手指的长度;对于大拇指,将前三个相邻骨骼点(2、3、4号骨骼点)的距离之和作为大拇指的长度。
手掌宽度网上存在不同的定义,根据普遍认可的两种定义,采用不同的算法进行测量。对于手掌宽度定义为四指并拢的指根处宽度,采用区域裁剪、水平投影、取中位数等操作来确定手掌的宽度;另外一种定义是五指并拢,整个手掌两侧的距离为手掌宽度,针对这种定义,直接确定合适的水平位置后进行水平投影得到宽度像素。值得注意的是,掩模图中的掌心位置可能存在参考圆,这时就需要对算法进行更新。
手腕宽度的测量考虑到手腕两侧边缘大致呈现出直线的特征,因此对手腕两侧的白色像素点进行一元线性回归,确定两侧直线的斜率后取斜率均值,作为两侧白色像素点的新斜率,这样可以保证两侧直线平行。已知两侧直线斜率,再直线分别过两侧白色像素点的中心像素坐标,确定两条直线的方程后计算平行线间的距离即为手腕宽度。
虎口角度的测量是根据上面在裁剪手指区域时得到的旋转角度进行计算。
六、实验内容
1. MediaPipe Hands介绍
MediaPipe Hands使用了机器学习的处理流程,该流程包括了两个模型:
- 手掌检测器:通过扫描全图,用一个有方向的手部定位框来定位手掌的位置
- 手部坐标模型:通过在手掌检测器裁剪的手部定位框上做操作,返回高保真的2.5D坐标
提供给手部坐标模型的是精确裁剪的手掌图片,极大的降低数据增强(例如旋转,平移和缩放)操作,可以使模型的性能都用来提高坐标定位的精度。在实时追踪的场景中,当前帧的手部定位框是从上一帧的手部关键点坐标预测中推导出来,这样可以避免每一帧都使用手掌检测器。 手掌检测器只在第一帧或者当手部丢失情况下才使用。
1.1 手部检测器
-
训练了一个手掌检测器来代替手部检测器:因为估计手掌和拳头等刚性物体的边界框比检测包含铰接手指的手要明显简单的多。
-
使用非极大值抑制算法:因为手掌是小物体,即使在如握手等双手自遮挡的情况下NMS都可以工作的很好。
-
只使用正方形的边界框来建模手掌:因为手掌是正方形的,这样就可以减少3到5倍的其他比例的锚框。
-
使用了类似于FPN(特征金字塔网络)编解码特征提取器:因为这样可以在更大的场景下对上下文进行感知,这样大物体和小物体都能在不同尺度的特征下被感受到(Tips:YOLOV3也是使用了FPN的思想提高了小目标的检测能力,因为大特征图里面的一个元素的值的感受野比较小,适合检测小物体。小特征图每个元素的感受野大,适合检测大物体。)
-
训练过程中使用了FocalLoss:因为能够支撑由大尺度方差产生出来的锚框。
1.2 手部坐标预测模型
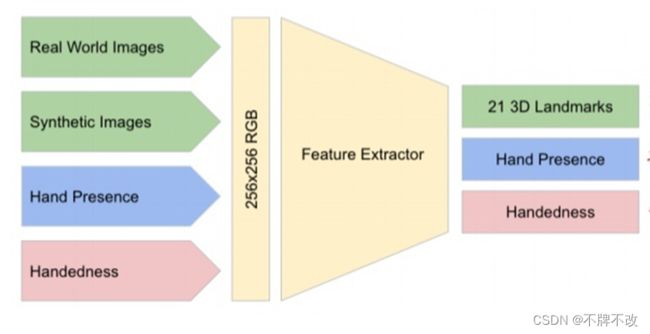
手掌检测器在全图上检测完之后,检测关键点坐标的模型通过回归来预测手部2.5D的关键点坐标。关键点坐标回归模型学到了内在的一致性手部姿态表示,因此在手部部分缺失或者自遮挡的情况下表现出非常好的鲁棒性,模型有三个输出(见图3)图 3
三类输出:
- 手部21个关键点坐标(见图4)
(1)从真实世界的图片和合成的图片中学习到二维坐标 X,Y
(2)从合成数据中学习到相对于手腕的三维深度坐标 Z - 手存在的置信度
(1)目的:为了从跟踪失败中恢复
(2)来源:手部跟踪模型会额外输出这个手是否出现的置信度
(3)使用:当输出的置信度低于阈值,则重置跟踪,重新使用手掌检测器;如果高于置信度,继续执行下面的手部关键点坐标的输出 - 左右手的二分类
(1)开发了一个二分类的分类头来判断输入的手是左手还是右手
图 4
2. 裁剪手掌部分
2.1 确定手掌的倾斜角度
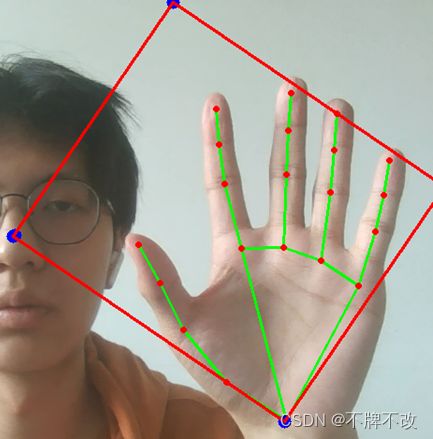
为了方便后续对手掌相关信息进行测量,我们将手掌从摄像头捕获的图像中裁剪出来,但是考虑到捕获到的手掌存在倾斜的情况,如果通过水平矩形区域将手掌完整裁剪,会包含很多背景像素,一定程度上会影响手掌区域的提取。最初对21个关键点计算最小外接矩形,但是由于描述掌心的关键点过少,出现了最小外接矩形无法框选出整个手掌(见图5)
图 5
我们决定自行设计算法确定矩形框,保证矩形框随着手的倾斜而倾斜。考虑到四个中指关键点和掌心关键点大致在同一条直线上,且该直线的倾斜程度可以用于描述手掌的倾斜程度。因此,计算四个中指关键点分别于掌心关键点所在直线的倾斜角度,如果非竖直的直线不少于三条,则计算全部非垂直直线的角度均值作为手掌中线的倾斜角度;如果非竖直的直线有两条,即存在两个中指关键点与掌心关键点构成的直线竖直,则计算两条直线的角度与MAXANGLE计算均值(其中MAXANGLE为斜率为1e6对应的角度,这是因为tan90°不存在),从实际意义出发,因为存在两个中指骨骼点与掌心骨骼点构成的直线竖直,所以垂直角度(即pi/2)也应该占据一定的权重;从计算的角度出发,如果一条非竖直直线的角度为-x,另一条非竖直直线的角度为x,则若不考虑pi/2,则二者计算均值为0,这显然与预期角度不符,而加上pi/2之后就很好地解决了该问题;其余情况下,由于存在较多竖直的直线,说明矩形框竖直的可能性比较大,所以直接设置为最大角度。最后根据角度计算斜率。
提出这个想法的过程并非一帆风顺的,最初我们采用斜率而非倾斜角度来获取矩形框时,发现很多数学计算会报错,旋转对应角度以保证手掌竖直时,当手掌大致竖直时会发现获取到的矩形框很容易偏离实际情况(见图6),这主要是因为tanx在x趋近于pi/2时变化非常快,导致斜率变化很大,所以在计算斜率均值时,尽管倾斜角度只变化了0.1°,而斜率可能变化了10的5次方数量级,这严重影响斜率的计算,所以提出了采用倾斜角度的想法。
图 6
2.2 确定完整手掌所在区域
计算出斜率后,根据掌心关键点坐标确定手掌中线的函数表达式,计算该直线与以掌心关键点为圆心,以四个中指关键点、掌心关键点相邻两点的距离之和为半径的圆的交点,距离中指最上端关键点近的交点作为矩形框上边界所过的点,掌心关键点作为矩形框下边界所过的点。遍历全部的关键点,确定离手掌中线最远的两侧的点,分别作为矩形框左、右边界所过的点,根据数学公式计算出矩形框的四个顶点坐标(见图7)。
图 7
另外,通过图7可以看出如此得到的矩形框无法将手腕比较完整地包含,且由于关键点都是位于手掌内部的,所以矩形框的边界肯定也会穿过手指,无法将手指完整地包含。因此,我们对该矩形进行放大,在竖直和水平方向上向外延伸,考虑到上下延伸的长度应该与手掌竖直方向上的长度有关(成比例),故将掌心关键点沿手掌中线向上移动了palmlength/10后再以palmlength+palmlength/6为半径画圆与中线的交点作为上边界所经过的点,左右延伸则是向外延伸“palmwidth”的倍数,此处的“palmwidth”并非实际的手掌宽度,只是一个代称,即关键点2、5、9、13、17相邻两个关键点的距离之和,我们认为延伸的长度应该与该距离成比例,分别向左右两侧延伸了0.04*palmwidth。如此确定最终的矩形框位置(见图8)。图8中黄点为边界经过的点,蓝点为矩形框顶点。
图 8
2.3 裁剪手掌区域
考虑到如果检测到的手掌距离摄像头非常远,那么窗口中显示的手掌图像也会非常小,在进行膨胀腐蚀等图像处理等操作时对小图像长度等信息的测量影响会比较大,所以对手掌进行放大非常有必要。对手掌进行旋转和平移是方便确定每根手指的位置,进而测量手指长度。
上面已经计算出手掌的倾斜角度,根据倾斜角度将其旋转至竖直,但是需要注意当手指朝下时,需要根据指尖的关键点的y坐标与掌心关键点的y坐标的大小关系来判断手指是否朝下,如果朝下需要特殊处理一下旋转角度。
根据数学公式确定手掌矩形框的中心,将中心移动到窗口中心位置后从而保证手掌位于窗口中心位置。
手掌放大的倍数取矩形框高度与窗口高度的比值和矩形框宽度与窗口宽度的比值的较大者的倒数,这样可以保证窗口尽量被手掌占满,同时我们的程序还允许水平显示整个手掌,这是考虑到手掌一般为长度大于宽度,而窗口(摄像头视野)是宽度大于长度,所以水平放置能更大地显示手掌。
最后将矩形框外的部分设置为黑色即可。
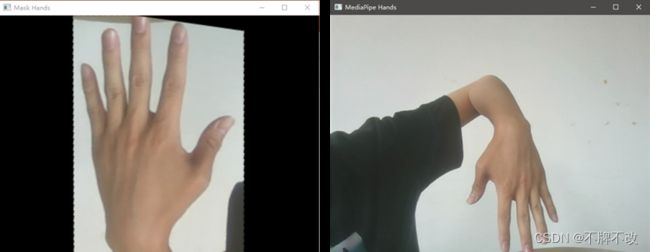
图 9 摄像头捕获(左)和裁剪出的小手掌(右)
图 10 摄像头捕获(左)和裁剪出的大手掌(右)
图 11 摄像头捕获(左)和裁剪出的倾斜手掌(右)
图 12 摄像头捕获(左)和裁剪出的反向手掌(右)
2.4 手掌边缘提取和获取手掌掩模图
2.4.1 颜色检测
颜色检测主要由两部分组成,一是肤色检测,检测出人体皮肤颜色,即找出手掌;二是硬币颜色检测,检测出硬币轮廓及其所在位置。
肤色检测就是在需要检测的图片中利用算法找出人体皮肤像素,将肤色像素与非肤色像素划分开的过程。
每种彩色模型都具有自己独特的特点,相互之间可以转换,可以根据实际需要选择不同的彩色模型来方便达到想要的效果。RGB 是最常见的一种与设备相关的色彩模型。由于人眼中棒状细胞和锥状细胞对红、绿、蓝三原色较敏感也就形成用 RGB 来表示颜色的色彩系统。YCrCb即YUV,主要用于优化彩色视频信号的传输,使其向后相容老式黑白电视。与RGB视频信号传输相比,它最大的优点在于只需占用极少的频宽(RGB要求三个独立的视频信号同时传输)。其中“Y”表示明亮度,也就是灰阶值;而“U”和“V”表示的则是色度,作用是描述影像色彩及饱和度,用于指定像素的颜色。“亮度”是透过RGB输入信号来建立的,方法是将RGB信号的特定部分叠加到一起。“色度”则定义了颜色的两个方面─色调与饱和度,分别用Cr和Cb来表示。其中,Cr反映了RGB输入信号红色部分与RGB信号亮度值之间的差异。而Cb反映的是RGB输入信号蓝色部分与RGB信号亮度值之间的差异。
YCrCb模型和RGB模型的相互转换关系如下
[ Y C b C r ] = [ 0.299 0.587 0.114 − 0.1687 − 0.3313 0.5 0.5 − 0.4187 − 0.0813 ] ⋅ [ R G B ] + [ 0 128 128 ] \left[ \begin{matrix} Y \\ Cb \\ Cr \end{matrix} \right]= \left[ \begin{matrix} 0.299 & 0.587 & 0.114 \\ -0.1687 & -0.3313 & 0.5 \\ 0.5 & -0.4187 & -0.0813 \end{matrix} \right]· \left[ \begin{matrix} R \\ G \\ B \end{matrix} \right]+ \left[ \begin{matrix} 0 \\ 128 \\ 128 \end{matrix} \right] ⎣ ⎡YCbCr⎦ ⎤=⎣ ⎡0.299−0.16870.50.587−0.3313−0.41870.1140.5−0.0813⎦ ⎤⋅⎣ ⎡RGB⎦ ⎤+⎣ ⎡0128128⎦ ⎤
[ R G B ] = [ 1 0 1.402 1 − 0.34414 − 0.71414 1 1.772 0 ] ⋅ [ Y C b − 128 C r − 128 ] \left[ \begin{matrix} R \\ G \\ B \end{matrix} \right]= \left[ \begin{matrix} 1 & 0 & 1.402 \\ 1 & -0.34414 & -0.71414 \\ 1 & 1.772 & 0 \\ \end{matrix} \right]· \left[ \begin{matrix} Y \\ Cb-128 \\ Cr-128 \end{matrix} \right] ⎣ ⎡RGB⎦ ⎤=⎣ ⎡1110−0.344141.7721.402−0.714140⎦ ⎤⋅⎣ ⎡YCb−128Cr−128⎦ ⎤
2.4.2 肤色检测
在研究肤色检测时,采用了四种肤色检测模型进行测试,分别为基于RGB颜色空间的肤色检测模型、基于HSV颜色空间的肤色检测模型、椭圆肤色检测模型、YCrCb颜色空间的Cr分量+Otsu法阈值分割算法。
基于RGB颜色空间的肤色检测模型
使用N帧静态背景逐像素建立背景模型,将当前帧与背景模型比较,计算亮度偏差和色度偏差,设置合适的阈值,根据阈值将像素点分为前景/背景。经过基于RGB颜色空间的肤色检测模型处理后的结果:

图 13 原图(左)、处理后(中)和二值化(右)
基于HSV颜色空间的肤色检测模型
RGB立方体模型是三维的HSV颜色模型的原型,色调(H)、饱和度(S)、明度(V)是在这个特征模型中的三个参数。经过HSV(Hue Saturation Value)颜色空间的肤色检测模型处理后的结果:
图 14 原图(左)、处理后(中)和二值化(右)
椭圆肤色检测模型
通过将二维空间获取得到的肤色信息映射到 YCrCb 二维空间中,从而可以得到椭圆颜色分布中的肤色信息。因此,我们只要通过这样方法就可以判断每一个坐标( Cr , Cb )都是否位于椭圆内,如果这个坐标不位于椭圆内,则可以认为这个坐标点不是一个皮肤像素的位置,否则就可以认为这个坐标点不是一个皮肤像素的位置。经过椭圆肤色检测模型处理后的结果:
图 15 原图(左)、处理后(中)和二值化(右)
YCrCb颜色空间的Cr分量+Otsu法阈值分割算法
图像由前景色和背景色组成,通过统计学的方法来选取一个能够将前景色和背景色尽可能的分开阈值。otsu算法中利用最大类间方差 来判断并选取最合适的阈值。经过YCrCb颜色空间的Cr分量+Otsu法阈值分割算法处理后的结果:
图 16 原图(左一)、处理后(左二)、Cr通道(右二)二值化(右一)
图 17 RGB(左一)、HSV(左二)、椭圆肤色检测(右二)和YCrCb+Ostu法(右一)
从以上四种肤色检测算法模型处理得到的结果来看,无论哪一种模型都或多或少有图像噪声,其中基于HSV(Hue Saturation Value)颜色空间的肤色检测模型处理后会有较多的图像噪声,处理效果最差;基于YCrCb颜色空间的Cr分量+Otsu法阈值分割算法处理后图像噪声最少,处理效果最好。
2.4.3 模糊处理
根据肤色检测部分研究发现,无论采用哪一种肤色检测算法模型都会受到一定程度上的图像噪声影响。所以,为了解决这个问题我们通常会采用图像模糊处理来减少图像噪声(或者说降低细节层次),即通过图像模糊可以将那些尺寸和亮度较小的物体过滤掉,较大的物体则易于检测。
在实验研究实现过程中,我尝试了四种模糊处理方法,即均值滤波模糊、中值滤波模糊、高斯滤波模糊以及双边滤波模糊。
- 均值滤波原理:在图像上通过对目标像素点周边8个像素的全体平均值来代替目标像素点的值。
- 中值滤波原理:把目标图像中每一个像素点的值用该像素点的邻域中各个像素点值的中值代替,从而消除孤立的噪声点。
- 高斯滤波原理:为了有效消除高斯噪音,可采用基于线性平滑滤波的高斯模糊滤波。在图像通过对每一个目标像素点周围邻域内的像素点值的加权平均值来代替这个像素点的值。
- 双边滤波原理:将图像的空间临近度和像素值相似度进行折中处理,于此同时再结合空域信息和灰度相似性,最终达到保边去噪的效果。
对比以上四种模糊处理后的结果发现,在本实验中,中值滤波模糊处理的效果最好,不仅能够有效消除图像中的噪声,而且能够最大程度的保证图像特征。
2.4.4 形态梯度学处理
基本思想:通过测量或提取目标图像中相应的形状或特征,并进行图像分析和目标识别的图像处理技术。形态学方法的基础是集合论,由J.Serra于1964年提出。形态学处理操作包括:腐蚀(Erosion)、膨胀(Dilation)、开运算(Opening)、闭运算(Closing)、白色顶帽变换(white top-hat)、黑色顶帽变换(black top-hat)
我们的实验主要用到了开运算、闭运算和形态学梯度处理。
- 开运算:
原理:先腐蚀运算,再膨胀运算。
(1)开运算能够除去孤立的小点,毛刺和小桥,而总的位置和形状不便。
(2)开运算是一个基于几何运算的滤波器。
(3)结构元素大小的不同将导致滤波效果的不同。
(4)不同的结构元素的选择导致了不同的分割,即提取出不同的特征。 - 闭运算:
原理:先膨胀运算,再腐蚀运算。
(1)闭运算能够填平小湖(即小孔),弥合小裂缝,而总的位置和形状不变。
(2)闭运算是通过填充图像的凹角来滤波图像的。
(3)结构元素大小的不同将导致滤波效果的不同。
(4)不同结构元素的选择导致了不同的分割。
我们先通过开运算去掉孤立的小点,再通过闭运算填充手掌内部的细小空洞,最后采用形态学梯度处理获取到手掌边缘。在光线理想的情况下效果极佳(见图18)。
图 18 掩模图(左)和边缘(右)
后续更新算法,对于提取手部掩模图,我们考虑到仅使用YCrCb+Ostu方法会存在某些较亮的区域尽管颜色与肤色相近,但无法被识别的情况,所以尝试获取RGB色彩空间内的手掌掩模图,将其与YCrCb+Ostu方法得到的掩模图取并集(即对应位置取较大像素)。如此,在RGB色彩空间中获取的手掌掩膜只要保证取出的部分一定是手掌部分,那么取并后就可以在一定程度上补充YCrCb+Ostu方法无法取到的较亮手掌区域,同时设置较大的阈值可以保证RGB色彩空间的掩模图不引入新的噪声。
图 19 理想环境下YCrCb(左)和RGB+YCrCb(右)
如图20所示,引入了RGB色彩空间的掩模图后,得到的最终掩模图非但没有变得纯净,反而引入了新的噪声,初步的猜想是因为RGB空间的阈值设定与实际显示有一定的出入,遂抛弃这种想法直接使用YCrCb得到的掩模图。
图 20 强光照环境下YCrCb(左)和RGB+YCrCb(右)
3. 手掌各个部位像素长度的测量
3.1 手掌宽度
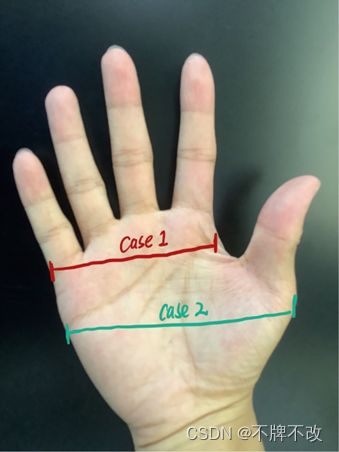
考虑到手掌宽度的定义有所不同,我们分两种情况来计算掌宽。
第一种是网上普遍认可的掌宽的定义,即四指伸直并拢,将大拇指移至小拇指的指根处,测量四根手指指根位置的宽度。
图 21 手掌宽度的两种定义
我们基于上面经过处理后始终保持竖直的手掌掩模图进行裁剪,确定测量手掌宽度的有关区域后,将该部分裁剪出来。对裁剪得到的图像向右水平投影(即水平方向累加,注意这里的累加是0或1的累加不是0或255的累加,也就是说需要先转换为0、1高维数组,之后的相似名称概念类似),水平投影得到的值对应于裁剪出的图像的每一行白色像素的个数,也即手掌的像素宽度。对于多个值,我们选取中位数作为手掌测量的像素宽度,以降低大面积噪声导致计算出错的可能性。
这部分算法的核心在于确定裁剪区域的边界。
上、下边界的确定是在水平中线的基础上加上一定的偏移量计算得到,水平中线的位置(即行号或y坐标)为四根手指的指根处骨骼点y坐标的均值,由于手掌保持竖直,故取均值可以减少单离群骨骼点对水平线定位的影响。上、下边界在水平中线的基础上分别减、加一定的偏移量,偏移量为 1/4 的非大拇指的四个手指的最长指关节(即最下面的)长度的均值,如此选择的原因在于,经过大量观察和测量发现,对于竖直的手掌而言,从水平中线位置向上、下偏移上述偏移量完全能够将待测量区域囊括。
在确定左、右边界之前,要明确手掌的大拇指在图像中的位置可能位于手掌左侧,也可能位于手掌右侧,这取决于摄像头拍摄的是手背还是手心,因此“左”和“右”的概念不再过多区分,而是将x坐标小的像素点认为处于左侧,x坐标大的像素点认为处于右侧。为了讲解方便,我们理解为右手的大拇指位于左侧,小拇指位于右侧,即右手的掌心面向摄像头。我们将大拇指根部的骨骼点(即编号为2的骨骼点)的x坐标视为左边界,该位置一定可以包括测量手掌宽度的相关区域,但是对于大拇指外撇程度较小,贴合食指程度较大的情况可能会引入影响手掌宽度计算的大拇指掩膜区域中的白像素。另外,被拍摄者必须保证掌心的“参考圆”必须不能出现在裁剪区域中,只需要避免圆过大,且向手腕尽量保持在手掌中心位置尽量靠近即可。尽管小拇指与图像边框之间的几乎没有白色像素存在,但是由于存在左、右颠倒的情况,所以不能直接以右侧的图像边框为右边界。由于中指指根骨骼点(9号骨骼点)与小拇指指根骨骼点(17号骨骼点)的相对位置可以确定小拇指位于手掌的左侧还是右侧,所以我们直接采用9号骨骼点关于17号骨骼点的对称点的x坐标作为右边界,如果可以保证该右边界一定是小拇指与同小拇指距离最近的垂直方向的图像边界之间的某个x坐标。之所以不使用与9号骨骼点类似位置的13号骨骼点,是为了保证右边界一定能将手掌的右边缘包含进来,而且由于小拇指右侧的像素具有比较纯净、噪声少的特点,所以向外多裁剪一部分也没有很大的影响。
图 22 掩模图(左)、手掌测量相关区域(中)和摄像头捕获(右)
考虑可能出现的特殊情况,当大拇指与食指的贴合程度比较大时,会裁剪出如下区域:
图 23 掩模图(左)、特殊情况下手掌测量相关区域(中)和摄像头捕获(右)
如图23(中)所示,大拇指的部分白色像素被裁剪进来,采用上述的水平投影的算法会出现误差,为了解决这个问题,可以采用从图像竖直中线开始对于每一行像素,分别确定从中线向两侧遇到的第一个黑色像素点,两个像素点的差视为该行像素对应的手掌宽度,这样可以避免水平投影将非法大拇指区域的像素计算在内的问题。
(这部分的优化算法虽然可以比较轻松地实现出来,但是我们认为没有必要,因为完全可以由被拍摄者加以注意来避免。而且,采用这种思路还可能出现新的问题,比如存在非大拇指的四个手指的指缝为黑色像素,如果将该区域也裁剪到区域中,那么会导致算法找到的第一个黑色像素并非我们期待的像素,从而又引起了误差)
第二种手掌宽度的定义是五指并拢后手掌最左侧到最右侧的距离。对于这种定义我们直接采用2号骨骼点所在的水平线位置的宽度像素作为该定义下的手掌宽度,但是可以看到该水平线大概率穿过掌心的参考圆,而参考圆在掩模图中的显示为黑色像素,因此采用上面水平投影的算法计算得到的宽度像素显然是存在较大误差的。因此,我们更换思路,直接使用np.where()函数确定这一行全部的白色像素的位置,将最左侧的白色像素和最右侧的白色像素之间的距离视为手掌宽度像素。直观上来看,该算法受噪声影响严重,但是向前思考几步,我们可以很轻松地获得的比较理想的手掌掩模图,即保证不存在偏离手掌严重或者孤立的噪声点,因此,完全可以应用该算法,只是在该定义下的手掌宽度对应的计算思路可以再优化一下,不局限于考虑一条水平线上的像素。
3.2 手腕宽度
需要使用到残差分析的知识。
3.3.1 残差分析
残差分析定义:在回归模型 y = β 0 + β 1 x + ε y=\beta_0+\beta_1x+\varepsilon y=β0+β1x+ε 中,假定 ε \varepsilon ε 的期望值为0,方差相等且服从正态分布的一个随机变量。但是,若关于 ε \varepsilon ε 的假定不成立,此时所做的检验以及估计和预测也许站不住脚。确定有关 ε \varepsilon ε 的假定是否成立的方法之一是进行残差分析(residual analysis)。
残差(residual)是因变量的观测值y_i与根据估计的回归方程求出的预测 y ^ i \widehat{y}_i y i 之差,用 e e e 表示。反映了用估计的回归方程去预测 y i y_i yi 而引起的误差。第 i i i 个观察值的残差为: e i = y i − y ^ i e_i=y_i-\widehat{y}_i ei=yi−y i。
常用残差图:有关 x x x 残差图、有关 y ^ \hat{y} y^ 的残差图和标准化残差图。有关 x x x 残差图:用横轴表示自变量x的值,纵轴表示对应残差 e i = y i − y ^ i e_i=y_i-\widehat{y}_i ei=yi−y i,每个x的值与对应的残差用图上的一个点来表示。
标准化残差:对于 ε \varepsilon ε 正态性假定的检验,也可通过标准化残差分析完成。标准化残差(standardized residual)是残差除以其标准差后得到的数值,也称Pearson残差或半学生化残差(semi-studentized residuals),用 z e z_e ze 表示。第 i i i个观察值的标准化残差为: z e i = e i s e = y i − y ^ i s e z_{e_i}=\frac{e_i}{s_e}=\frac{y_i-\widehat{y}_i}{s_e} zei=seei=seyi−y i( s e s_e se 是残差的标准差的估计)。如果误差项 ε \varepsilon ε 服从正态分布的这一假定成立,则标准化残差的分布也服从正态分布。大约有95%的标准化残差在 -2~2 之间。
3.3.2 实现思路
手腕宽度测量的最初思路为先将手腕部分的区域裁剪出来,一元线性拟合手腕左侧边缘像素点所在直线与手腕右侧边缘所在直线,通过标准化残差分析去掉离群点,对于剩下的点再一次进行一元线性拟合。取手腕两侧直线斜率的均值作为新的斜率,以计算得到的斜率为手腕两侧直线的新的斜率,分别过两侧点的中线点,从而确定了两条平行的直线,两条平行线的距离为手腕的宽度。
我们将0号骨骼点下面的部分视为手腕区域,将下面的部分裁剪出来。通过np.where()确定出最左、右侧边缘的白色像素点点集后进行残差分析。但是,经过标准化残差分析后发现全部的测试情况的全部像素点均无法保证标准化的残差在 ± 2 σ \pm2\sigma ±2σ 之内,也就是说对于任意一个像素点不是离群点连5%的把握都没有,这说明这些像素点不满足一元线性回归。
图 24 边缘(左)、手腕左侧边缘白色点旋转90°的排列(中)和标准化残差(右)
但是考虑到实际情况,手腕边缘确实应该可以通过一元线性表示出来。我们认为出现这种问题的原因在于以0号骨骼点下面的部分为手腕区域是不准确的,故更正这个区域的上边界为在0号骨骼点所在水平线的基础上向下偏移从0号骨骼点到图像底部距离的倍数。尝试了各种系数,甚至取到了0.9,即裁剪出的图像高度大约在5个像素左右,但是仍然被残差分析判定为离群点,故猜测,残差分析对于准确度的要求过高,不适合该情形,便抛弃采用残差分析的思路。
我们直接对去掉一部分后裁剪出的图像中的手腕进行一元线性回归,得到两侧直线的斜率,后续步骤按照上述最初思路进行即可。
3.3 手指宽度
测量手指宽度的整体思路是根据每根手指的倾斜角度确定整个手掌掩模图的旋转角度,对手掌进行旋转后将手指部分移至窗口中心位置,保证每根手指能够保持竖直且位于中心显示,将每根手指所在的大致中心区域裁剪出来。对于裁剪出来的手指掩模图进行分段投影以确定在不同指关节处的手指宽度。
测量手指宽度的核心在于裁剪手指区域,其大致思路与裁剪手掌区域类似,都需要经过相似的旋转和平移操作。
旋转的角度是根据每个手指上的四个骨骼点来确定的。计算手指上相邻两个骨骼点所在直线的倾斜角度,如此,一根手指上便可以得到三条直线对应的倾斜角度。对于大于一定角度的倾斜,我们将其归为MAXANGLE,进而我们将全部的倾斜情况分为三类,一类是MAXANGLE,另两类为角度为正和角度为负。采用一定的算法计算三条直线的角度均值。如果存在MAXANGLE,那么说明有一个指关节是竖直的,考虑实际情况,如果一根指关节为竖直的,那么大概率整根手指是处于倾斜程度比较小的情况,故我们直接认为该手指是竖直的,即倾斜角度的均值直接设置为MAXANGLE;不存在的MAXANGLE时,如果正角度的数量多,那么就对正角度的倾斜角计算均值作为角度均值,否则使用全部负角度的倾斜角计算均值。得到倾斜角度后,可以确定斜率,规定该直线过中间指关节的中点,即中间两个骨骼点的中点,这样便确定了手指所在直线。同样地,我们根据该中点移动到裁剪窗口的中心位置的移动距离确定手指区域移动的距离,保证手指位于窗口中心位置,如图25所示。
图 25 按照五根手指对手掌进行旋转和平移后
显然,还需要将手指区域裁剪出来。根据手指四个骨骼点的距离之和确定要裁剪出的区域的高度和宽度,这只需要让距离之和乘以一定的比例系数即可。另外,考虑到后续对手指区域掩模图处理时使用骨骼点更加方便,我们同时计算出了在旋转和平移后的图像中手指骨骼点的位置,计算出的新骨骼点位置如图26所示。
图 26 显示骨骼点
首先说明,我们认为不同指关节处的手指宽度是不同的,所以测量每根手指靠近指尖的三个骨骼点所在水平线的手指宽度,并进行显示。
裁剪出手指区域后,对被裁剪出的每根手指的掩模图进行竖直方向的投影,投影如图27所示。具体的投影细节为将每根手指靠近指尖的三个骨骼点所在水平线上面的全部像素投影到该水平线上。由于可能存在相邻手指贴合程度比较大的情况,即手指区域中出现了另一根手指的部分白像素,如图28所示。
图 27 手指指关节投影图
图 28 一张掩模图出现多根手指
对于这种情况,不能简单地将投影后的累积白像素值进行相加从而认为是手指的宽度像素。我们的思路是对于每一个骨骼点所在水平线上的投影,枚举一条竖直直线所在列,分别找直线左侧的第一个黑色像素和右侧的第一个像素,所谓第一个是指离直线最近的一个黑色像素。每次枚举都计算找到的两个黑色像素的距离作为手指的宽度像素,取全部枚举方案的最大手指宽度像素作为该骨骼点处手指的最终宽度像素。
这样可以保证不会将非目标手指的白色像素考虑在内,因为每一段连续的被裁剪进来的非目标手指白色像素的宽度一定不会比目标手指的白色像素的宽度要长,而枚举考虑到了目标手指可能出现偏离中心的情况,保证了算法的健壮性。
不得不提到一点,在进行数据处理时,要尽量采用numpy的切片等操作,避免使用for、while循环。在动态捕捉时,稍微多点的循环就会导致捕获事件非常卡顿,而numpy内部实现的函数进行“循环”的速度要比手写循环快得多,可以有效地避免卡顿的发生。
3.4 手指长度
手指长度的定义为指尖到对应虎口的最长距离。根据观察,我们认为对于食指、中指、无名指和小拇指而言,其长度为四个相邻手指骨骼点间的距离之和,而对于大拇指而言,其长度为靠近指尖的三个相邻骨骼点间的距离之和。
提供一种未实现的优化算法。可以充分利用在测量“手指宽度”时获取的每根手指的掩模图。可以确定该掩模图一定会将虎口区域也裁剪进来,因此,我们可以在竖直方向上进行投影,像素累积值的突变点就是虎口位置。确定好手指两侧的虎口竖直位置(x坐标)后,在虎口竖直位置的像素列从下向上找第一个黑色像素,该黑色像素为两侧虎口上面的第一个黑色像素,如此可以完整地确定出虎口所在坐标,根据两个虎口的y坐标的较小者作为裁剪区域的下边界,虎口x坐标为左右边界,上边界依然是当前区域的上边界,将仅包含手指的区域从手指区域中裁剪出来,用新的手指掩模图高度减去其中y坐标最小的白色像素的y坐标值即为手指长度。需要注意,如果操作对象是大拇指和小拇指,那么显然不存在两个虎口,但是这并不影响计算,因为竖直方向上的投影仍然存在累积值的突变。
概念图展示如下:
图 29 根据虎口裁剪前(上) 和根据虎口裁剪后(下)
3.5 虎口角度
上面在裁剪手指区域时计算过每根手指变为到竖直方向需要旋转的角度,那么只要根据旋转的角度计算出相邻两个手指之间的夹角,就相当于计算出了虎口的角度。
唯一需要注意的一点就是旋转角度是0 ~ 360°之间的,而我们需要先将其转换为-180° ~ 180°之间,再计算相邻手指之间的角度差值取绝对值即为手指间的夹角,又即虎口角度。
4. 像素长度转换为实际长度
4.1 霍夫圆检测
霍夫圆变换的基本思路是认为图像上每一个非零像素点都有可能是一个潜在的圆上的一点,跟霍夫线变换一样,也是通过投票,生成累积坐标平面,设置一个累积权重来定位圆。
在笛卡尔坐标系中圆的方程为:
( x − a ) 2 + ( y − b ) 2 = r 2 \left(x-a\right)^2+\left(y-b\right)^2=r^2 (x−a)2+(y−b)2=r2
极坐标描述为:
x = a + r c o s θ y = b + r s i n θ x=a+rcos\theta \\ y=b+rsin\theta x=a+rcosθy=b+rsinθ
即:
a = x − r c o s θ b = y − r s i n θ a=x-rcos\theta \\ b=y-rsin\theta a=x−rcosθb=y−rsinθ
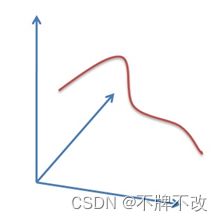
故,在 a − b − r a-b-r a−b−r组成的三维坐标系中,一个点可以唯一确定一个圆。而在笛卡尔的 x − y x-y x−y坐标系中经过某一点的所有圆映射到 a − b − r a-b-r a−b−r坐标系中就是一条三维的曲线:
图 30
经过 x − y x-y x−y坐标系中所有的非零像素点的所有圆就构成了 a − b − r a-b-r a−b−r坐标系中很多条三维的曲线。在 x − y x-y x−y坐标系中同一个圆上的所有点的圆方程是一样的,它们映射到 a − b − r a-b-r a−b−r坐标系中的是同一个点,所以在 a − b − r a-b-r a−b−r坐标系中该点就应该有圆的总像素个曲线相交。通过判断 a − b − r a-b-r a−b−r中每一点的相交(累积)数量,大于一定阈值的点就认为是圆。
以上是标准霍夫圆变换实现算法,问题是它的累加面试一个三维的空间,意味着比霍夫线变换需要更多的计算消耗。Opencv霍夫圆变换对标准霍夫圆变换做了运算上的优化。它采用的是“霍夫梯度法”。它的检测思路是去遍历累加所有非零点对应的圆心,对圆心进行考量。如何定位圆心呢?圆心一定是在圆上的每个点的模向量上,即在垂直于该点并且经过该点的切线的垂直线上,这些圆上的模向量的交点就是圆心。霍夫梯度法就是要去查找这些圆心,根据该“圆心”上模向量相交数量的多少,根据阈值进行最终的判断。
图 31
4.2 测距原理
规定: - 物体实际大小为D,待求 - 参考圆实际半径为R,已知 - 放大比例为k,已知 - 摄像头捕捉到的物体像素大小d,已知 - 摄像头捕捉到的参考圆像素半径r,已知根据公式:
D R = d ∗ k r ∗ k = d r \frac{D}{R}=\frac{d\ast k}{r\ast k}=\frac{d}{r} RD=r∗kd∗k=rd
故,
D = d r ∗ R D=\frac{d}{r}\ast R D=rd∗R
因此,只要测量出手掌部位的像素长度后除以参考圆的半径再乘以参考圆实际长度就可以计算出手掌部位的实际长度了。
4.3 检测掌心参考圆效果
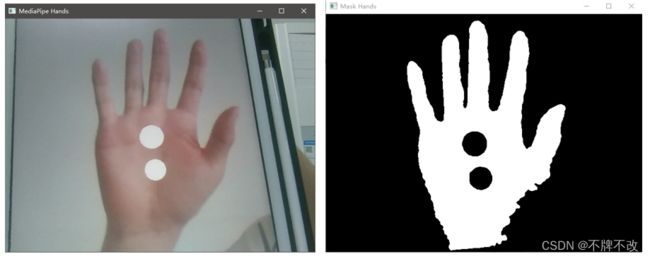
对于掌心存在两个圆的情况,我们只选最大的圆,之所以考虑这种情况,是因为在进行完图像处理时如果存在空洞噪声点,那么很可能会检测出多个圆,我们选取最大圆是为了确定检测出的圆中的参考圆。
图 32 摄像头捕获图像(左) 和多个圆的手掌掩膜图(右)
考虑到采用电脑摄像头进行手掌捕获,而在手掌中心贴硬币比较困难,所以我们选用圆规画的半径为1cm的圆形纸片贴在手掌中心位置作为参考圆。另外,对于识别到手掌却未识别到参考圆时,我们设置返回None,不进行任何操作,仅显示用户提示信息。
七、效果展示
动态图 1 存在手掌矩形框抖动的问题(已解决)
动态图 2 手掌矩形框展示
动态图 3 参考圆位于手掌内测时测量手掌相关数据的(掩模图及其他)展示图
动态图 4 参考圆位手掌背部时测量手掌相关数据的(掩模图及其他)展示图
动态图 5 参考圆位手掌内测时测量手掌相关数据的(边缘图及其他)展示图
动态图 6 参考圆位手掌背部时测量手掌相关数据的(边缘图及其他)展示图
动态图 7 霍夫圆检测与手指区域裁剪(掩模图及其他)展示图
动态图 8 霍夫圆检测与手指区域裁剪(边缘图及其他)展示图
八、参考资料
【1】arXiv:2006.10214
【2】Hands - mediapipe (google.github.io)
【3】张懿, 刘旭, 李海峰. 数字RGB与YCbCr颜色空间转换的精度[J]. 江南大学学报:自然科学版, 2007, 6(2):3.
【4】摄像头单目测距原理及实现
【5】残差分析(残差原理与标准化残差分析)
【6】阈值化+hsv hsv通道分离
【7】opencv仿射变换实现图像旋转缩放
【8】Matplotlib 中文文档
【9】NumPy Documentation
九、全部代码
由于时间比较长了,记不清每个部分的顺序了,可能比较混乱。
baseline.py 是基础程序段,main.py 就是在 baseline.py 的基础上修改得到的,无需运行 baseline.py ,只需要在 main.py 运行即可。
可能即使去掉某些程序也可以顺利运行。
baseline.py
"""
作者:LJR
日期:2022 05 17
"""
import cv2
import mediapipe as mp
mp_drawing = mp.solutions.drawing_utils
mp_hands = mp.solutions.hands
hands = mp_hands.Hands(
static_image_mode=False,
max_num_hands=2,
min_detection_confidence=0.75,
min_tracking_confidence=0.75)
cap = cv2.VideoCapture(0, cv2.CAP_DSHOW)
while True:
ret, frame = cap.read()
frame = cv2.cvtColor(frame, cv2.COLOR_BGR2RGB)
frame= cv2.flip(frame,1) # 镜像翻转
results = hands.process(frame)
frame = cv2.cvtColor(frame, cv2.COLOR_RGB2BGR)
if results.multi_handedness:
for hand_label in results.multi_handedness:
# print(hand_label)
pass
if results.multi_hand_landmarks:
for hand_landmarks in results.multi_hand_landmarks:
# print('hand_landmarks:', hand_landmarks)
# 关键点可视化
mp_drawing.draw_landmarks(
frame, hand_landmarks, mp_hands.HAND_CONNECTIONS)
cv2.imshow('MediaPipe Hands', frame)
if cv2.waitKey(1) & 0xFF == 27:
break
cap.release()
main.py
"""
作者:LJR
日期:2022 05 18
"""
import cv2
import mediapipe as mp
from programentry import *
mp_drawing = mp.solutions.drawing_utils
mp_hands = mp.solutions.hands
hands = mp_hands.Hands(
static_image_mode=False,
max_num_hands=2,
min_detection_confidence=0.75,
min_tracking_confidence=0.75)
cap = cv2.VideoCapture(0, cv2.CAP_DSHOW)
while True:
ret, frame = cap.read()
H, W, C = frame.shape
frame = cv2.cvtColor(frame, cv2.COLOR_BGR2RGB)
frame= cv2.flip(frame,1) # 镜像翻转
results = hands.process(frame)
frame = cv2.cvtColor(frame, cv2.COLOR_RGB2BGR)
if results.multi_hand_landmarks:
for hand_landmarks in results.multi_hand_landmarks:
# mp_drawing.draw_landmarks(
# frame, hand_landmarks, mp_hands.HAND_CONNECTIONS)
lms = [] # 21骨骼点
for landmarks in hand_landmarks.landmark:
lms.append((int(landmarks.x * W), int(landmarks.y * H))) # 图像中的坐标
programentry(frame, lms) # 将手和手腕裁剪出来
else: # 没检测出手掌时呈现黑屏
cv2.imshow("Mask Hands", np.zeros_like(frame, dtype=np.uint8))
cv2.imshow("Hough Circles", np.zeros((200, 200), dtype=np.uint8))
PANEL_H, PANEL_W = 270, 120
panel = np.zeros((PANEL_H, PANEL_W), dtype=np.uint8)
cv2.imshow("thumb", panel)
cv2.imshow("index", panel)
cv2.imshow("middle", panel)
cv2.imshow("ring", panel)
cv2.imshow("little", panel)
cv2.imshow('MediaPipe Hands', frame)
if cv2.waitKey(1) & 0xFF == 27:
break
cap.release()
programentry.py
"""
作者:LJR
日期:2022 05 18
"""
from crophand import *
from cropfigers import *
from edgeextraction import *
from measurepalmandwristwidth import measurepalmandwristwidth
from measurefingerslengthwidth import measurefingerslengthwidth
from measureanglebetweenfingers import measureanglebetweenfingers
def programentry(frame, lms):
cv2.namedWindow("Mask Hands")
cv2.namedWindow("MediaPipe Hands")
cv2.namedWindow("Hough Circles")
cv2.namedWindow("thumb")
cv2.namedWindow("index")
cv2.namedWindow("middle")
cv2.namedWindow("ring")
cv2.namedWindow("little")
handmask, lmsaftertransform, ratio = crophand(frame, lms) # 获取手掌
handedge, handmask = edgeextraction(handmask, lmsaftertransform, ratio)
# 边缘和掩模图
fingermaskandlms = cropfigers(handmask, lmsaftertransform, 'all') # 每个手指的mask展示
# fingermaskandlms 包含三个numpy,第一个是每个手指的掩模图,第二个是掩模图中lms位置,第三个是保持手指竖直需要旋转的角度
cv2.imshow("Mask Hands", handedge) # 一切绘图操作都必须在imshow之前
"""
调用函数实现计算长度、宽度等
"""
measurefingerslengthwidth(handedge, handmask, lmsaftertransform, fingermaskandlms)
measurepalmandwristwidth(handedge, handmask, lmsaftertransform)
measureanglebetweenfingers(handedge, handmask, lmsaftertransform, fingermaskandlms)
crophand.py
"""
作者:LJR
日期:2022 05 20
"""
import cv2
import numpy as np
from math import *
MAX = 1e6 # 不能设置太大,会出现对负数开根的情况
MAXANGLE = atan(MAX) # 最大斜率对应的角度(弧度制)
"""
在图像处理中的坐标系
x
(0,0) —— —— —— —— >
|
|
|
y v
"""
def angle(p1, p2):
"""
两点确定直线的角度(弧度制)
注意:如果直线与x轴垂直则返回一个无穷大的正数;如果直线与y轴垂直则返回一个无穷小的正数(而非0)
这样做的目的是在获取与该直线垂直的直线的斜率时避免出现分母为0的分类讨论
这里最初的思路是返回斜率,但是由于tan(x)在x趋于pi/2和-pi/2的时候变化率过大,导致在计算斜率均值时会因为存在一个比较大的斜率导致斜率均值变化非常大,从而出现矩形框抖动的问题
优化思路是放弃斜率均值,而采用角度均值,最后再将角度转化为对应的斜率即可,成功结果大幅抖动问题,但毕竟还是与类似于+89°和-89°相差2°的问题,所以还是存在小幅抖动
:param p1: 一个元组,包含横坐标和纵坐标
:param p2: 一个元组,包含横坐标和纵坐标
:return: 确定的直线的角度(弧度制)
"""
if p1[1] == p2[1]: # 因为坐标只能是整数,所以直接判等
return 1 / MAX # 不设置为0,而是设置为无穷小的正数,方便计算其对应的垂线
elif p1[0] == p2[0]:
return MAX # 设置为无穷大的正数
else:
return atan((p1[1] - p2[1]) / (p1[0] - p2[0]))
def averageline(lms):
"""
计算中指上的四个骨骼点分别与掌心骨骼点构成的四条直线的斜率均值
:param lms: 21个关键点(骨骼点)
:return: 斜率均值
"""
neg = []
pos = []
for i in range(9, 13, 1):
_ = angle(lms[0], lms[i])
if _ != MAX:
if _ < 0:
neg.append(_) # 角度为正
else:
pos.append(_) # 角度为负
notmaxnumber = len(neg) + len(pos)
if notmaxnumber == 4 or notmaxnumber == 3: # 非垂直的直线个数为3或4
"""
如果角度为负和角度为正的直线哪个组直线个数多,那么就计算组内直线的角度均值,作为手掌中线角度;
如果个数相等,则计算两组的角度和的绝对值,绝对值大的组内直线的角的均值作为手掌中线角度;
如果绝对值相等,那么直接将手掌中线角度设置为pi/2,也就是MAXANGLE
"""
if len(neg) > len(pos):
averageangle = sum(neg) / len(neg)
elif len(neg) < len(pos):
averageangle = sum(pos) / len(pos)
elif fabs(sum(neg)) > fabs(sum(pos)):
averageangle = sum(neg) / len(neg)
elif fabs(sum(neg)) < fabs(sum(pos)):
averageangle = sum(pos) / len(pos)
else:
averageangle = MAXANGLE
elif notmaxnumber == 2:
"""
如果只存在两条非垂直直线,则计算两条直线的角度与MAXANGLE计算均值
从实际意义出发,因为存在两个中指骨骼点与掌心骨骼点构成的直线竖直,所以垂直角度(即pi/2)也应该占据一定的权重;
从计算的角度出发,如果一条非垂直直线的角度为-x,另一条非垂直直线的角度为x,则若不考虑pi/2,则二者计算均值为0,这显然与预期角度不符,
而加上pi/2之后就很好地解决了该问题
"""
averageangle = (MAXANGLE + sum(neg) + sum(pos)) / (len(neg) + len(pos) + 1)
else:
"""
由于垂直直线比较多,说明矩形框竖直的可能性比较大,所以直接设置为最大角度
"""
averageangle = MAXANGLE # ≈ pi/2
x, y = lms[0]
k = tan(averageangle)
b = y - k * x
return (k, b)
def pointtopointdistance(p1, p2):
"""
点到点的距离
:param p1: 一个元组,包含横坐标和纵坐标
:param p2: 一个元组,包含横坐标和纵坐标
:return: 浮点数,距离
"""
x1, y1 = p1
x2, y2 = p2
return sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)
def pointtolinedistance(p, l, absolute=False):
"""
点到直线的”距离“
注意:如果不取绝对值,则可以判断点位于直线的哪一侧
:param p: 一个元组,包含横坐标和纵坐标
:param l: 一个元组,包含斜率和截距
:param absolute: 布尔类型,距离是否取绝对值
:return: 点到直线的”距离“
"""
x, y = p
k, b = l
return (abs(k * x + b - y) if absolute else k * x + b - y) / (k ** 2 + 1)
def setpointwithdistance(p, line, dist):
"""
以p为圆心,以dist为半径画圆,与直线line的两个交点坐标
联立公式:
y = k*x+b
d^2 = (x-x0)^2 + (y-y0)^2
最后采用求根公式
:param p: 一个元组,包含横坐标和纵坐标
:param line: 一个元组,包含斜率和截距
:param dist: 距离(半径)
:return: 返回两个点的坐标
"""
cx, cy = p
k, b = line
aa = k ** 2 + 1 # 注意^表示按位异或,**表示幂乘
bb = 2 * (k * b - k * cy - cx)
cc = cx ** 2 + (b - cy) ** 2 - dist ** 2
det = bb ** 2 - 4 * aa * cc
x1 = (-bb + sqrt(det)) / (2 * aa)
y1 = k * x1 + b
x2 = (-bb - sqrt(det)) / (2 * aa)
y2 = k * x2 + b
p1 = (int(x1), int(y1))
p2 = (int(x2), int(y2))
# p1 = (x1, y1)
# p2 = (x2, y2)
return p1, p2
def pointwithdistance(lms, line):
"""
计算四个确定点的坐标
:param lms: 21个关键点(骨骼点)
:param line: 一个元组,包含斜率和截距
:return: 包含四个坐标(元组)的列表
"""
d_palmlength = 0 # 中指骨骼点、手掌点之间的距离和
for idx in range(9, 13, 1):
d_palmlength += pointtopointdistance(lms[idx], lms[0 if idx is 9 else idx - 1])
d_palmwidth = 0 # 大拇指最下面的骨骼点(2)、食指(5)、中指(9)、无名指(13)、小拇指(17)之间的距离和
for idx in range(5, 18, 4):
d_palmwidth += pointtopointdistance(lms[idx], lms[2 if idx is 5 else idx - 1])
"""
上下延伸的长度应该与手掌竖直方向上的长度成比例(有关)
"""
p1, p2 = setpointwithdistance(lms[0], line, d_palmlength / 10)
# 距离中指顶端远的为用于确定矩形框下边界的点
bottompoint = p1 if pointtopointdistance(p1, lms[12]) > pointtopointdistance(p2, lms[12]) else p2
p1, p2 = setpointwithdistance(bottompoint, line, d_palmlength + d_palmlength / 6)
# 距离中指顶端近的为答案
toppoint = p1 if pointtopointdistance(p1, lms[12]) < pointtopointdistance(p2, lms[12]) else p2
"""
最初设想:
左右延伸的长度:(掌心面向镜头)
向左延伸:与大拇指超出矩形框的部分应该与骨骼点3和4的斜率有关,倾斜越严重,那么出界的部分越多。
最右端的骨骼点坐标延手掌中线垂直方向向外延伸手掌宽度的倍数,该倍数与骨骼点3,4的斜率或角度有关。
向左延伸:与大拇指类似,只不过这里的对象是小拇指。
暂时实现:
直接按照掌宽的固定比例,后续可以根据效果进行优化
"""
leftpoint = rightpoint = bottompoint
leftdist = rightdist = 0
for p in lms:
dist = pointtolinedistance(p, line)
if dist < leftdist:
leftpoint = p
leftdist = dist
elif dist > rightdist:
rightpoint = p
rightdist = dist
p1, p2 = setpointwithdistance(leftpoint, (-1 / line[0], getlinebais(leftpoint, -1 / line[0])),
d_palmwidth * thumbdistancefunction(pointtopointdistance(lms[3], lms[4])))
leftpoint = p1 if pointtopointdistance(p1, toppoint) > pointtopointdistance(p2, toppoint) else p2 # 距离掌心中线上顶点远的点
p1, p2 = setpointwithdistance(rightpoint, (-1 / line[0], getlinebais(rightpoint, -1 / line[0])),
d_palmwidth * pinkydistancefunction(pointtopointdistance(lms[19], lms[20])))
rightpoint = p1 if pointtopointdistance(p1, toppoint) > pointtopointdistance(p2, toppoint) else p2 # 距离掌心中线上顶点远的点
return toppoint, leftpoint, bottompoint, rightpoint
def thumbdistancefunction(x):
return 0.06
def pinkydistancefunction(x):
return 0.06
def getlinebais(p, k):
"""
已知点坐标和直线斜率,求确定的直线截距
:param p: 一个元组,包含横坐标和纵坐标
:param k: 直线斜率
:return: 截距
"""
x, y = p
return y - k * x
def intersectionpoint(l1, l2):
"""
已知两条直线,求交点坐标
:param l1: 一个元组,包含斜率和截距
:param l2: 一个元组,包含斜率和截距
:return: 一个元组,包含横坐标和纵坐标
"""
k1, b1 = l1
k2, b2 = l2
return ((b1 - b2) / (k2 - k1), (k2 * b1 - k1 * b2) / (k2 - k1))
def findcontours(points, middleline):
"""
确定矩形的四个顶点
:param points: 四个确定点(黄色)
:param middleline: 手掌中线,一个元组,包含斜率和截距
:return: 包含四个坐标(元组)的列表
"""
lines = []
k, b = middleline
for idx, p in enumerate(points):
_k = -1.0 / k if idx % 2 == 0 else k
lines.append((_k, getlinebais(p, _k)))
contours = [] # 右上,左上,左下,右下
for i in range(len(lines)):
contours.append(intersectionpoint(lines[i], lines[-1] if i is 0 else lines[i - 1]))
return contours
def getarea(contours):
"""
计算矩形框面积
:param contours: 确定点坐标
:return: 面积
"""
# 数学方法计算矩形面积
# from crophand import pointtopointdistance
# print(pointtopointdistance(contours[0], contours[1]) * pointtopointdistance(contours[1], contours[2]))
# 调用函数计算矩形面积
# print(cv2.contourArea(contours))
return cv2.contourArea(contours)
def getcenter(contours):
"""
计算矩形框中心坐标
:param contours: 确定点坐标
:return: 坐标,一个元组
"""
# 数学方法计算矩形中心
# cx = (contours[1][0] + contours[-1][0]) / 2
# cy = (contours[1][1] + contours[-1][1]) / 2
# print(cx, cy)
# 调用函数计算矩形中心
m = cv2.moments(contours)
cx = int(m['m10'] / m['m00'])
cy = int(m['m01'] / m['m00'])
# print(cx, cy)
return (cx, cy) # 与通过边相乘计算出的面积差不多
"""
后续可以将程序优化成智能切换水平显示和竖直显示
"""
def gettheta(contours, degree, horizontal=False):
"""
计算旋转角度
:param contours: 确定点坐标
:param degree: 当前角度(弧度制)
:param horizontal: 是否进行水平显示
:return: 旋转角度(角度制)
"""
upsidedown = True if contours[0][1] > contours[-1][1] else False
degree = degree * 180 / pi # 转换为角度制
degree = 90 + degree + (180 if degree >= 0 else 0) # degree<0:degree+=90 degree>0:degree+=270
if upsidedown:
degree += 180
if horizontal:
degree += 90
return degree
def getscale(contours, windowsize, horizontal):
"""
计算放大比例
:param contours: 确定点坐标
:param windowsize: 窗口大小,一个元组,(W, H)
:param horizontal: 是否进行水平显示
:return: 放大的比例
"""
W, H = windowsize
if horizontal:
H, W = W, H
# 水平方向和竖直方向上窗口长度与手掌长度的比值
ratio = min(1, max(pointtopointdistance(contours[0], contours[-1]) / H,
pointtopointdistance(contours[0], contours[1]) / W))
return 1 / ratio # 放大倍数就是1/比值
def pointrotate(p, cp, theta):
x, y = p
cx, cy = cp
theta = theta * pi / 180
# 逆时针
# rx = (x - cx) * cos(theta) - (y - cy) * sin(theta) + cx
# ry = (x - cx) * sin(theta) + (y - cy) * cos(theta) + cy
# 顺时针
rx = (x - cx) * cos(theta) + (y - cy) * sin(theta) + cx
ry = (y - cy) * cos(theta) - (x - cx) * sin(theta) + cy
return (rx, ry)
def transform(frame, lms, contours):
"""
实现将手永远显示在窗口的中间位置,且手的方向朝上,根据实际捕捉到的手的大小进行放大显示
:param frame: 窗口图像
:param contours: 矩形顶点坐标(右上,左上,左下,右下)
:return: 变形后的图像
"""
cx, cy = getcenter(contours)
H, W, C = frame.shape
dx, dy = W / 2 - cx, H / 2 - cy
horizontal = False # 是否将手水平显示
theta = gettheta(contours, angle(contours[1], contours[2]), horizontal)
scale = getscale(contours, (W, H), horizontal)
# 移动到中心
# 直接使用 M = np.float32([[cos, -sin, dx], [sin, cos, dy]])会与预期不符,所以将旋转和平移分开实现了
M = np.float32([[1, 0, dx], [0, 1, dy]])
frame = cv2.warpAffine(frame, M, (W, H))
# 旋转
M = cv2.getRotationMatrix2D((W / 2, H / 2), theta, 1) # 第一个参数是旋转中心
frame = cv2.warpAffine(frame, M, (W, H))
# 缩放
M = cv2.getRotationMatrix2D((W / 2, H / 2), 0, scale)
frame = cv2.warpAffine(frame, M, (W, H))
_lms = pointaftertransform(lms, (W, H), (dx, dy), theta, scale)
return frame, _lms, scale
def pointaftertransform(lms, windowsize, move, theta, scale):
"""
原图上的某个点坐标经过图像的平移、旋转和放大后的所在的位置
:param lms: 点集坐标
:param windowsize: 窗口(图像)大小
:param move: 水平平移距离和竖直平移距离
:param theta: 角度(角度制)
:param scale: 放大比例
:return: 点集坐标
"""
_lms = []
W, H = windowsize
dx, dy = move
for item in lms:
x, y = item
x, y = x + dx, y + dy # 移动
rx, ry = pointrotate((x, y), (W / 2, H / 2), theta) # 旋转
_x, _y = W / 2 + scale * (rx - W / 2), H / 2 + scale * (ry - H / 2)
_lms.append((int(_x), int(_y)))
return _lms
def crophand(frame, lms):
middleline = averageline(lms)
points = pointwithdistance(lms, middleline)
contours = findcontours(points, middleline)
contours = np.array(contours, dtype=np.int) # 转为int
"""
# 绘制出矩形框和一些点
for p in points:
cv2.circle(frame, p, 7, (0, 255, 255), cv2.FILLED) # 四个确定点(黄)
for x, y in contours:
cv2.circle(frame, (x, y), 7, (255, 0, 0), cv2.FILLED) # 矩形框的四个顶点(蓝)
for i in range(len(contours)):
cv2.line(frame, contours[i], contours[-1] if i is 0 else contours[i - 1], (0, 0, 255), 2) # 矩形边(红)
"""
# 无需绘制最小外接矩形,因为算出来的就是个矩形,直接画直线即可
# rect = cv2.minAreaRect(np.array(contours, dtype=np.int)) # 注意转换为整数
# points = np.int0(cv2.boxPoints(rect)) # 得到最小外接矩形的四个点坐标
# cv2.drawContours(frame, [points], 0, (0, 0, 255), 2) # 直接在原图上绘制矩形框
background = np.zeros_like(frame, dtype=np.uint8)
cv2.fillConvexPoly(background, contours, (255, 255, 255))
ORI = np.minimum(background, frame)
ORI, _lms, ratio = transform(ORI, lms, contours)
"""
for p in _lms:
cv2.circle(ORI, p, 7, (0, 0, 0), cv2.FILLED) # 必须位于imshow前面
"""
return ORI, _lms, ratio
edgeextraction.py
"""
作者:LJR
日期:2022 05 20
"""
import cv2
import numpy as np
from math import *
import functools
def getregionsize_tanh(section, x):
l, r = section
x = 1.5 * x + 1
return tanh(x) * (r - l) + l
def getregionsize_min(section, x):
l, r = section
return min((x - 1) * 3 + l, r)
"""
def check(pointcolor, thresh): # 速度太慢,无法采用
R, G, B = pointcolor
R, G, B = int(R), int(G), int(B)
thresh_R, diff_RG, diff_GB = thresh
if R < thresh_R[0] or R > thresh_R[1] or R - G < diff_RG[0] or R - G > diff_RG[1] or G - B < diff_GB[0] or G - B > \
diff_GB[1]:
return False
return True
def regiongrowth(frame, seeds, regionsize, bigthresh, smallthresh, p): # 速度太慢,无法采用
H, W, C = frame.shape
seedMark = np.zeros((H, W), dtype=np.uint8)
contour = []
for s in seeds:
idx, (x, y) = s
contour.append((max(0, int(y - regionsize)),
min(H - 1, int(y + regionsize)),
max(0, int(x - regionsize)),
min(W - 1, int(x + regionsize)))
)
# 八邻域
if p == 8:
next = [(-1, -1), (-1, 0), (-1, 1), (0, 1), (1, 1), (1, 0), (1, -1), (0, -1)]
elif p == 4:
next = [(-1, 0), (0, 1), (1, 0), (0, -1)]
# seeds内无元素时候生长停止
while len(seeds) != 0:
# 栈顶元素出栈
pt = seeds.pop(0)
idx, (x, y) = pt
# if not check(frame[y, x], bigthresh):
# continue
# print(len(seeds))
seedMark[y, x] = 255
# print(x, y)
topedge, bottomedge, leftedge, rightedge = contour[idx]
# print(topedge, bottomedge, leftedge, rightedge)
for i in range(p):
tx = x + next[i][0]
ty = y + next[i][1]
# 检测边界点
if tx < leftedge or ty < topedge or tx > rightedge or ty > bottomedge or seedMark[ty, tx] == 255:
continue
# 相邻的颜色必须小于一定的阈值
# frame_array = np.array(abs(frame[y, x] - frame[ty, tx]), dtype=np.uint8)
# smallthresh_array = np.array(smallthresh, dtype=np.uint8)
# if (frame_array < smallthresh_array).all():
# seeds.append((tx, ty))
seeds.append((idx, (tx, ty)))
return seedMark
"""
def gethandmask_RGB(frame, seeds, regionsize, thresh):
H, W, C = frame.shape
R, G, B = cv2.split(frame)
thresh_R, diff_RG, diff_GB = thresh
frame = np.array(frame, dtype=np.int)
region_bool = np.zeros(frame.shape[:-1], dtype=np.bool)
for s in seeds:
idx, (x, y) = s
top, bottom = max(0, int(y - regionsize)), min(H - 1, int(y + regionsize))+1
left, right = max(0, int(x - regionsize)), min(W - 1, int(x + regionsize))+1
region_bool[top:bottom, left:right] = True
color_bool = (R > thresh_R[0]) * (R < thresh_R[1]) * (R > G + diff_RG[0]) * (R < G + diff_RG[1]) * (G > B + diff_GB[0]) * (G < B + diff_GB[1])
boolarray = region_bool * color_bool
if boolarray.any(): # 当boolarray全false时取min、max会报错
adaptive_thresh_R = (min(R[boolarray]), max(R[boolarray]))
adaptive_diff_RG = (min(R[boolarray] - G[boolarray]), max(R[boolarray] - G[boolarray]))
adaptive_diff_GB = (min(G[boolarray] - B[boolarray]), max(G[boolarray] - B[boolarray]))
boolarray = (R > adaptive_thresh_R[0]) * (R < adaptive_thresh_R[1]) * (R > G + adaptive_diff_RG[0]) * (R < G + adaptive_diff_RG[1]) * (G > B + adaptive_diff_GB[0]) * (G < B + adaptive_diff_GB[1])
skin = np.zeros(frame.shape[:-1], dtype=np.uint8)
skin[boolarray] = 255
return skin
def edgeextraction(frame, lms, ratio):
lmsinframe = []
H, W, C = frame.shape
for mark in lms:
x, y = mark
if x >= 0 and y >= 0 and x < W and y < H:
idx = len(lmsinframe)
lmsinframe.append((idx, mark))
frame = cv2.cvtColor(frame, cv2.COLOR_BGR2RGB)
# YCrCb
YCrCb = cv2.cvtColor(frame, cv2.COLOR_RGB2YCR_CB)
(Y, Cr, Cb) = cv2.split(YCrCb)
Cr = cv2.GaussianBlur(Cr, (5, 5), 0)
_, skin_YCrCb = cv2.threshold(Cr, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)
skin_YCrCb = np.array(skin_YCrCb, dtype=np.uint8)
# RGB
regionsize = getregionsize_tanh((10, 20), ratio) / 2
thresh_R, diff_RG, diff_GB = (110, 256), (5, 40), (-10, 35)
# skin = regiongrowth(RGB, lmsinframe, regionsize, (thresh_R, diff_RG, diff_GB), (15, 15, 15), 8)
skin_RGB = gethandmask_RGB(frame, lmsinframe, regionsize, (thresh_R, diff_RG, diff_GB))
skin = np.maximum(skin_RGB, skin_YCrCb) # 两种检测方法取并
# skin = skin_YCrCb
median_bur = cv2.medianBlur(skin_YCrCb, 5) # 中值滤波模糊
# 中值滤波模糊处理的效果最好,不仅能够有效消除图像中的噪声,而且能够最大程度的保证图像特征。
kernel = np.ones((3, 3), np.uint8) # 设置卷积核
edge = cv2.morphologyEx(median_bur, cv2.MORPH_GRADIENT, kernel) # 形态梯度学处理
opening = cv2.morphologyEx(median_bur, cv2.MORPH_OPEN, (20, 20)) # 开运算:去除孤立点
closing = cv2.morphologyEx(opening, cv2.MORPH_CLOSE, (10, 10)) # 闭运算:连通
mask = closing
# 提取边缘
# edge = cv2.morphologyEx(closing, cv2.MORPH_GRADIENT, (3, 3)) # 形态梯度学处理
# edge = cv2.Canny(closing, 100, 250) # 效果比较好
# # contour_x, contour_y = np.where(edge == 255) # 返回值为横坐标列表和列坐标列表
# # contour = np.dstack((contour_x, contour_y))[0] # 拼接成坐标
# 返回mask表示掩模图(手掌部分为白色)
# 返回edge表示手掌边缘图(只有手掌边缘为白色)
# 还是直接显示YCrCb效果好
return edge, mask
cropfigers.py
"""
作者:LJR
日期:2022 06 27
"""
import cv2
import numpy as np
from math import *
MAX = 1e6 # 不能设置太大,会出现对负数开根的情况
MAXANGLE = atan(MAX) # 最大斜率对应的角度(弧度制)
PANEL_H, PANEL_W = 270, 120
def angle(p1, p2):
"""
两点确定直线的角度(弧度制)
注意:如果直线与x轴垂直则返回一个无穷大的正数;如果直线与y轴垂直则返回一个无穷小的正数(而非0)
这样做的目的是在获取与该直线垂直的直线的斜率时避免出现分母为0的分类讨论
这里最初的思路是返回斜率,但是由于tan(x)在x趋于pi/2和-pi/2的时候变化率过大,导致在计算斜率均值时会因为存在一个比较大的斜率导致斜率均值变化非常大,从而出现矩形框抖动的问题
优化思路是放弃斜率均值,而采用角度均值,最后再将角度转化为对应的斜率即可,成功结果大幅抖动问题,但毕竟还是与类似于+89°和-89°相差2°的问题,所以还是存在小幅抖动
:param p1: 一个元组,包含横坐标和纵坐标
:param p2: 一个元组,包含横坐标和纵坐标
:return: 确定的直线的角度(弧度制)
"""
if p1[1] == p2[1]: # 因为坐标只能是整数,所以直接判等
return 1 / MAX # 不设置为0,而是设置为无穷小的正数,方便计算其对应的垂线
elif p1[0] == p2[0]:
return MAX # 设置为无穷大的正数
else:
return atan((p1[1] - p2[1]) / (p1[0] - p2[0]))
def averageline(lms, idx):
"""
计算每根手指上的四个骨骼点相邻两个点所在的直线
:param lms: 21个骨骼点(numpy)
:param idx: 手指的4个骨骼点
:return: 一个元组,直线斜率和直线截距
"""
ismax = []
pos = []
neg = []
for i in idx[:-1]:
_ = angle(lms[i], lms[i + 1]) # 一般情况下是3个
if _ is MAX:
ismax.append(_)
elif _ > 0:
pos.append(_)
else:
neg.append(_)
"""
只要存在“垂直”的情况,就设置均角度为MAXANGLE,否则取正角度的均值与负角度的均值中斜线数量多者。
"""
if len(ismax) >= 1:
averageangle = MAXANGLE
elif len(pos) > len(neg):
averageangle = sum(pos) / len(pos)
else:
averageangle = sum(neg) / len(neg)
# 上面是防抖动处理
x, y = (lms[idx[1]] + lms[idx[2]]) / 2
k = tan(averageangle)
b = y - k * x
return (k, b)
def transform(frame, move, theta):
"""
对图像进行旋转和移动,保证被裁剪的手指位于图像中心位置
:param frame:
:param move:
:param theta:
:return:
"""
H, W = frame.shape
dx, dy = move
# 移动到中心
# 直接使用 M = np.float32([[cos, -sin, dx], [sin, cos, dy]])会与预期不符,所以将旋转和平移分开实现了
M = np.float32([[1, 0, dx], [0, 1, dy]])
frame = cv2.warpAffine(frame, M, (W, H))
# 旋转
M = cv2.getRotationMatrix2D((W / 2, H / 2), theta, 1) # 第一个参数是旋转中心
frame = cv2.warpAffine(frame, M, (W, H))
return frame
def pointrotate(p, cp, theta):
"""
点绕点旋转,即确定骨骼点绕图像旋转的中心旋转后的位置
(先旋转后平移)
:param p: 旋转前点的位置
:param cp: 旋转中心位置
:param theta: 旋转角度(角度制)
:return: 旋转后点的位置
"""
x, y = p
cx, cy = cp
theta = theta * pi / 180
# 顺时针
rx = (x - cx) * cos(theta) + (y - cy) * sin(theta) + cx
ry = (y - cy) * cos(theta) - (x - cx) * sin(theta) + cy
return (rx, ry)
def getfingermask(fingerframe, single_finger_lms, dist):
"""
将只包含手指的mask图返回(此时还未将手指放在新的窗口中)
:param fingerframe: 包含整个手掌的图像,经过了旋转和平移,对应手指在中心位置
:param dist: 对应手指四个骨骼点的距离和
:return: 返回仅含手指的mask
"""
H, W = fingerframe.shape
# 获取中指区域,并将中指区域裁剪出来,放在一个大小固定的窗口中心位置
fingerframe_H_from, fingerframe_H_to = int((H - dist) // 2), int((H + dist) // 2)
fingerframe_W_from, fingerframe_W_to = int((W - dist / 2.7) // 2), int((W + dist / 2.7) // 2)
fingerframe_H = fingerframe_H_to - fingerframe_H_from
fingerframe_W = fingerframe_W_to - fingerframe_W_from
frame = fingerframe[fingerframe_H_from:fingerframe_H_to, fingerframe_W_from:fingerframe_W_to]
dx, dy = PANEL_H / 2 - fingerframe_H / 2, PANEL_W / 2 - fingerframe_W / 2
M = np.float32([[1, 0, dx], [0, 1, dy]])
finger = cv2.warpAffine(frame, M, (PANEL_W, PANEL_H))
single_finger_lms -= (int(fingerframe_W_from), int(fingerframe_H_from)) # 经过裁剪,先算出骨骼点在裁剪出的窗口中的位置 !!!
single_finger_lms += (int(dx), int(dy)) # 再计算平移后的位置 !!!
return finger, single_finger_lms
def cropfigers(frame, lms, whichone):
"""
将手指mask放在一个新的固定大小的窗口中
:param frame: 手掌mask
:param lms: 手掌mask上骨骼点的位置
:param whichone: 'all'--全部手指 'thumb'--大拇指 'index'--食指 'middle'--中指 'ring'--无名指 'little'--小拇指
:return: 每个手指的掩模图
"""
# 错误参数处理
if whichone is not 'thumb' and whichone is not 'index' and whichone is not 'middle' and whichone is not 'ring' and whichone is not 'little' and whichone is not 'all':
print('【ERROR】 Invalid Input !')
whichone = 'all'
# 初始化五个手指的窗口变量
thumb = None
index = None
middle = None
ring = None
little = None
thumb_lms = None
index_lms = None
middle_lms = None
ring_lms = None
little_lms = None
lms = np.array(lms) # 转换为ndarray
lms_idx_list = np.array(np.arange(1, 21)).reshape((5, 4)) # 每个手指的骨骼点
fingerframe = []
H, W = frame.shape
_lms = []
thetas = []
for lms_idx in lms_idx_list:
cx, cy = (lms[lms_idx[1]] + lms[lms_idx[2]]) / 2 # 中心位置,用于计算移动距离的
dx, dy = W / 2 - cx, H / 2 - cy # 移动距离
k, b = averageline(lms, lms_idx)
degree = atan(k) * 180 / pi
theta = 90 + degree + (180 if degree >= 0 else 0) # 旋转角度
thetas.append(theta)
_ = transform(frame, (dx, dy), theta)
fingerframe.append(_)
# 确定骨骼点在变形后的图像中的位置:先让骨骼点绕原图中平移至图像中心的点的坐标旋转相同的角度后再平移相同的距离,得到变形后图像中骨骼点位置
tmp_lms = []
for i in lms_idx:
rx, ry = pointrotate(lms[i], (cx, cy), theta)
_x, _y = rx + dx, ry + dy
tmp_lms.append((int(_x), int(_y)))
_lms.append(tmp_lms)
_lms = np.array(_lms)
_lms_dist = np.sum(np.sqrt(np.sum(np.diff(_lms, axis=1) ** 2, axis=2)), axis=1) # 计算每个手指相邻两个点的距离之和
_lms_dist += _lms_dist / 10 # 保证整根手指都能被裁剪进来
_lms_dist = _lms_dist.astype(np.int64) # 转为int才能进行后续对图像的裁剪操作
if (whichone is 'thumb' or whichone is 'all'):
# lms : 1, 2, 3, 4
"""
# 为了观察变形后骨骼点的位置
for i in _lms[0]:
fingerframe[0][i[1]-5:i[1]+5, i[0]-5:i[0]+5] = 128
"""
thumb, thumb_lms = getfingermask(fingerframe[0], _lms[0], _lms_dist[0])
# cv2.imshow('hand_with_thumb_rotate', fingerframe[0])
cv2.imshow('thumb', thumb)
if (whichone is 'index' or whichone is 'all'):
# lms : 5, 6, 7, 8
"""
# 为了观察变形后骨骼点的位置
for i in _lms[1]:
fingerframe[1][i[1]-5:i[1]+5, i[0]-5:i[0]+5] = 128
"""
index, index_lms = getfingermask(fingerframe[1], _lms[1], _lms_dist[1])
# cv2.imshow('hand_with_index_rotate', fingerframe[1])
cv2.imshow('index', index)
if (whichone is 'middle' or whichone is 'all'):
# lms : 9, 10, 11, 12
"""
# 为了观察变形后骨骼点的位置
for i in _lms[2]:
fingerframe[2][i[1]-5:i[1]+5, i[0]-5:i[0]+5] = 128
"""
middle, middle_lms = getfingermask(fingerframe[2], _lms[2], _lms_dist[2])
# cv2.imshow('hand_with_middle_rotate', fingerframe[2])
cv2.imshow('middle', middle)
if (whichone is 'ring' or whichone is 'all'):
# lms : 13, 14, 15, 16
"""
# 为了观察变形后骨骼点的位置
for i in _lms[3]:
fingerframe[3][i[1]-5:i[1]+5, i[0]-5:i[0]+5] = 128
"""
ring, ring_lms = getfingermask(fingerframe[3], _lms[3], _lms_dist[3])
# cv2.imshow('hand_with_ring_rotate', fingerframe[3])
cv2.imshow('ring', ring)
if (whichone is 'little' or whichone is 'all'):
# lms : 17, 18, 19, 20
"""
# 为了观察变形后骨骼点的位置
for i in _lms[4]:
fingerframe[4][i[1]-5:i[1]+5, i[0]-5:i[0]+5] = 128 # 注意先i[1] 再i[0]!!!
"""
little, little_lms = getfingermask(fingerframe[4], _lms[4], _lms_dist[4])
# cv2.imshow('hand_with_litte_rotate', fingerframe[4])
cv2.imshow('little', little)
return (np.array([thumb, index, middle, ring, little]),
np.array([thumb_lms, index_lms, middle_lms, ring_lms, little_lms]),
np.array(thetas))
functions.py
"""
作者:LJR
日期:2022 05 18
"""
import cv2
import numpy as np
from math import *
MAX = 1e6 # 不能设置太大,会出现对负数开根的情况
MAXANGLE = atan(MAX) # 最大斜率对应的角度(弧度制)
"""
在图像处理中的坐标系
x
(0,0) —— —— —— —— >
|
|
|
y v
"""
def angle(p1, p2):
"""
两点确定直线的角度(弧度制)
注意:如果直线与x轴垂直则返回一个无穷大的正数;如果直线与y轴垂直则返回一个无穷小的正数(而非0)
这样做的目的是在获取与该直线垂直的直线的斜率时避免出现分母为0的分类讨论
这里最初的思路是返回斜率,但是由于tan(x)在x趋于pi/2和-pi/2的时候变化率过大,导致在计算斜率均值时会因为存在一个比较大的斜率导致斜率均值变化非常大,从而出现矩形框抖动的问题
优化思路是放弃斜率均值,而采用角度均值,最后再将角度转化为对应的斜率即可,成功结果大幅抖动问题,但毕竟还是与类似于+89°和-89°相差2°的问题,所以还是存在小幅抖动
:param p1: 一个元组,包含横坐标和纵坐标
:param p2: 一个元组,包含横坐标和纵坐标
:return: 确定的直线的角度(弧度制)
"""
if p1[1] == p2[1]: # 因为坐标只能是整数,所以直接判等
return 1/MAX # 不设置为0,而是设置为无穷小的正数,方便计算其对应的垂线
elif p1[0] == p2[0]:
return MAX # 设置为无穷大的正数
else:
return atan((p1[1] - p2[1]) / (p1[0] - p2[0]))
def averageline(lms):
"""
计算中指上的四个骨骼点分别与掌心骨骼点构成的四条直线的斜率均值
:param lms: 21个关键点(骨骼点)
:return: 斜率均值
"""
neg = []
pos = []
for i in range(9, 13, 1):
_ = angle(lms[0], lms[i])
if _ != MAX:
if _ < 0:
neg.append(_) # 角度为正
else:
pos.append(_) # 角度为负
notmaxnumber = len(neg)+len(pos)
if notmaxnumber == 4 or notmaxnumber == 3: # 非垂直的直线个数为3或4
"""
如果角度为负和角度为正的直线哪个组直线个数多,那么就计算组内直线的角度均值,作为手掌中线角度;
如果个数相等,则计算两组的角度和的绝对值,绝对值大的组内直线的角的均值作为手掌中线角度;
如果绝对值相等,那么直接将手掌中线角度设置为pi/2,也就是MAXANGLE
"""
if len(neg) > len(pos):
averageangle = sum(neg) / len(neg)
elif len(neg) < len(pos):
averageangle = sum(pos) / len(pos)
elif fabs(sum(neg)) > fabs(sum(pos)):
averageangle = sum(neg) / len(neg)
elif fabs(sum(neg)) < fabs(sum(pos)):
averageangle = sum(pos) / len(pos)
else:
averageangle = MAXANGLE
elif notmaxnumber == 2:
"""
如果只存在两条非垂直直线,则计算两条直线的角度与MAXANGLE计算均值
从实际意义出发,因为存在两个中指骨骼点与掌心骨骼点构成的直线竖直,所以垂直角度(即pi/2)也应该占据一定的权重;
从计算的角度出发,如果一条非垂直直线的角度为-x,另一条非垂直直线的角度为x,则若不考虑pi/2,则二者计算均值为0,这显然与预期角度不符,
而加上pi/2之后就很好地解决了该问题
"""
averageangle = (MAXANGLE + sum(neg) + sum(pos)) / (len(neg) + len(pos) + 1)
else:
"""
由于垂直直线比较多,说明矩形框竖直的可能性比较大,所以直接设置为最大角度
"""
averageangle = MAXANGLE # ≈ pi/2
x, y = lms[0]
k = tan(averageangle)
b = y - k * x
return (k, b)
def pointtopointdistance(p1, p2):
"""
点到点的距离
:param p1: 一个元组,包含横坐标和纵坐标
:param p2: 一个元组,包含横坐标和纵坐标
:return: 浮点数,距离
"""
x1, y1 = p1
x2, y2 = p2
return sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)
def pointtolinedistance(p, l, absolute=False):
"""
点到直线的”距离“
注意:如果不取绝对值,则可以判断点位于直线的哪一侧
:param p: 一个元组,包含横坐标和纵坐标
:param l: 一个元组,包含斜率和截距
:param absolute: 布尔类型,距离是否取绝对值
:return: 点到直线的”距离“
"""
x, y = p
k, b = l
return (abs(k * x + b - y) if absolute else k * x + b - y) / (k ** 2 + 1)
def pointwithdistance(lms, line):
"""
与掌心骨骼点距离为d,位于以斜率均值为斜率且过掌心骨骼点的直线上的点的坐标
联立公式:
y = k*x+b
d^2 = (x-x0)^2 + (y-y0)^2
最后采用求根公式
:param lms: 21个关键点(骨骼点)
:param line: 一个元组,包含斜率和截距
:return: 所求点的坐标,一个元组,包含横坐标和纵坐标
"""
d = 0 # 中指骨骼点、手掌点之间的距离和
for idx in range(9, 13, 1):
d += pointtopointdistance(lms[idx], lms[0 if idx is 9 else idx - 1])
print(d)
cx, cy = lms[0]
k, b = line
aa = k ** 2 + 1 # 注意^表示按位异或,**表示幂乘
bb = 2 * (k * b - k * cy - cx)
cc = cx ** 2 + (b - cy) ** 2 - d ** 2
det = bb ** 2 - 4 * aa * cc
x1 = (-bb + sqrt(det)) / (2 * aa)
y1 = k * x1 + b
x2 = (-bb - sqrt(det)) / (2 * aa)
y2 = k * x2 + b
p1 = (int(x1), int(y1)) # 注意转换为整数
p2 = (int(x2), int(y2)) # 注意转换为整数
return p1 if pointtopointdistance(p1, lms[12]) < pointtopointdistance(p2, lms[12]) else p2 # 距离标记点12近的为答案
def getlinebais(p, k):
"""
已知点坐标和直线斜率,求确定的直线截距
:param p: 一个元组,包含横坐标和纵坐标
:param k: 直线斜率
:return: 截距
"""
x, y = p
return y - k * x
def intersectionpoint(l1, l2):
"""
已知两条直线,求交点坐标
:param l1: 一个元组,包含斜率和截距
:param l2: 一个元组,包含斜率和截距
:return: 一个元组,包含横坐标和纵坐标
"""
k1, b1 = l1
k2, b2 = l2
return ((b1 - b2) / (k2 - k1), (k2 * b1 - k1 * b2) / (k2 - k1))
def findcontours(lms, toppoint, middleline):
"""
确定矩形的四个点
:param lms: 21个关键点
:param toppoint: 已经求出的与掌心骨骼点距离为d的点
:param middleline: 手掌中线,一个元组,包含斜率和截距
:return: 包含四个坐标(元组)的列表
"""
leftpoint = rightpoint = lms[0]
leftdist = rightdist = 0
for p in lms:
dist = pointtolinedistance(p, middleline)
if dist < leftdist:
leftpoint = p
leftdist = dist
elif dist > rightdist:
rightpoint = p
rightdist = dist
lines = []
k, b = middleline
# print(k)
lines.append((-1.0/k, getlinebais(toppoint, -1.0/k)))
lines.append((k, getlinebais(leftpoint, k)))
lines.append((-1.0/k, getlinebais(lms[0], -1.0/k)))
lines.append((k, getlinebais(rightpoint, k)))
contours = []
for i in range(len(lines)):
contours.append(intersectionpoint(lines[i], lines[-1] if i is 0 else lines[i-1]))
return contours
def crophand(frame, lms):
middleline = averageline(lms)
toppoint = pointwithdistance(lms, middleline)
cv2.circle(frame, toppoint, 7, (255, 0, 0), cv2.FILLED) # 确定的上边界点
contours = findcontours(lms, toppoint, middleline)
contours = np.array(contours, dtype=np.int) # 转为int
for x, y in contours:
cv2.circle(frame, (x, y), 7, (255, 0, 0), cv2.FILLED)
for i in range(len(contours)):
cv2.line(frame, contours[i], contours[-1] if i is 0 else contours[i-1], (0, 0, 255), 2)
# 无需绘制最小外接矩形,因为算出来的就是个矩形,直接画直线即可
# rect = cv2.minAreaRect(np.array(contours, dtype=np.int)) # 注意转换为整数
# points = np.int0(cv2.boxPoints(rect)) # 得到最小外接矩形的四个点坐标
# cv2.drawContours(frame, [points], 0, (0, 0, 255), 2) # 直接在原图上绘制矩形框
# plotinfinitystones(frame, lms) # 无限宝石!
def plotinfinitystones(frame, lms):
"""
!!!慎重调用该函数,可能导致地球一半的人消失!!!
"""
# 0:黄 2:绿 5:粉 9:蓝 13:红 17:橙
d = pointtopointdistance(lms[0], lms[9])
bigstonesize = (d/3.8, d/4)
smallstonesize = (d/6.3, d/7)
x, y = lms[0]
y -= d/3.5
points = np.array([[x, y-bigstonesize[0]], [x+bigstonesize[1]/2, y-bigstonesize[0]/2], [x+bigstonesize[1]/2, y+bigstonesize[0]/2], [x, y+bigstonesize[0]], [x-bigstonesize[1]/2, y+bigstonesize[0]/2], [x-bigstonesize[1]/2, y-bigstonesize[0]/2]], dtype=np.int)
cv2.fillConvexPoly(frame, points, (24,255,255))
# 2:绿
x, y = lms[2]
points = np.array([[x, y - smallstonesize[0]], [x + smallstonesize[1] / 2, y - smallstonesize[0] / 2], [x + smallstonesize[1] / 2, y + smallstonesize[0] / 2], [x, y + smallstonesize[0]], [x - smallstonesize[1] / 2, y + smallstonesize[0] / 2], [x - smallstonesize[1] / 2, y - smallstonesize[0] / 2]], dtype=np.int)
cv2.fillConvexPoly(frame, points, (120, 255, 40))
# 5:粉
x, y = lms[5]
points = np.array([[x, y - smallstonesize[0]], [x + smallstonesize[1] / 2, y - smallstonesize[0] / 2],
[x + smallstonesize[1] / 2, y + smallstonesize[0] / 2], [x, y + smallstonesize[0]],
[x - smallstonesize[1] / 2, y + smallstonesize[0] / 2],
[x - smallstonesize[1] / 2, y - smallstonesize[0] / 2]], dtype=np.int)
cv2.fillConvexPoly(frame, points, (240, 60, 209))
# 9:蓝
x, y = lms[9]
points = np.array([[x, y - smallstonesize[0]], [x + smallstonesize[1] / 2, y - smallstonesize[0] / 2],
[x + smallstonesize[1] / 2, y + smallstonesize[0] / 2], [x, y + smallstonesize[0]],
[x - smallstonesize[1] / 2, y + smallstonesize[0] / 2],
[x - smallstonesize[1] / 2, y - smallstonesize[0] / 2]], dtype=np.int)
cv2.fillConvexPoly(frame, points, (240, 230, 50))
# 13:红
x, y = lms[13]
points = np.array([[x, y - smallstonesize[0]], [x + smallstonesize[1] / 2, y - smallstonesize[0] / 2],
[x + smallstonesize[1] / 2, y + smallstonesize[0] / 2], [x, y + smallstonesize[0]],
[x - smallstonesize[1] / 2, y + smallstonesize[0] / 2],
[x - smallstonesize[1] / 2, y - smallstonesize[0] / 2]], dtype=np.int)
cv2.fillConvexPoly(frame, points, (37, 15, 240))
# 17:橙
x, y = lms[17]
points = np.array([[x, y - smallstonesize[0]], [x + smallstonesize[1] / 2, y - smallstonesize[0] / 2],
[x + smallstonesize[1] / 2, y + smallstonesize[0] / 2], [x, y + smallstonesize[0]],
[x - smallstonesize[1] / 2, y + smallstonesize[0] / 2],
[x - smallstonesize[1] / 2, y - smallstonesize[0] / 2]], dtype=np.int)
cv2.fillConvexPoly(frame, points, (44, 160, 255))
functions2.py
"""
作者:LJR
日期:2022 05 18
"""
import cv2
import numpy as np
from math import *
MAX = 1e6 # 不能设置太大,会出现对负数开根的情况
MAXANGLE = atan(MAX) # 最大斜率对应的角度(弧度制)
"""
在图像处理中的坐标系
x
(0,0) —— —— —— —— >
|
|
|
y v
"""
def angle(p1, p2):
"""
两点确定直线的角度(弧度制)
注意:如果直线与x轴垂直则返回一个无穷大的正数;如果直线与y轴垂直则返回一个无穷小的正数(而非0)
这样做的目的是在获取与该直线垂直的直线的斜率时避免出现分母为0的分类讨论
这里最初的思路是返回斜率,但是由于tan(x)在x趋于pi/2和-pi/2的时候变化率过大,导致在计算斜率均值时会因为存在一个比较大的斜率导致斜率均值变化非常大,从而出现矩形框抖动的问题
优化思路是放弃斜率均值,而采用角度均值,最后再将角度转化为对应的斜率即可,成功结果大幅抖动问题,但毕竟还是与类似于+89°和-89°相差2°的问题,所以还是存在小幅抖动
:param p1: 一个元组,包含横坐标和纵坐标
:param p2: 一个元组,包含横坐标和纵坐标
:return: 确定的直线的角度(弧度制)
"""
if p1[1] == p2[1]: # 因为坐标只能是整数,所以直接判等
return 1/MAX # 不设置为0,而是设置为无穷小的正数,方便计算其对应的垂线
elif p1[0] == p2[0]:
return MAX # 设置为无穷大的正数
else:
return atan((p1[1] - p2[1]) / (p1[0] - p2[0]))
def averageline(lms):
"""
计算中指上的四个骨骼点分别与掌心骨骼点构成的四条直线的斜率均值
:param lms: 21个关键点(骨骼点)
:return: 斜率均值
"""
neg = []
pos = []
for i in range(9, 13, 1):
_ = angle(lms[0], lms[i])
if _ != MAX:
if _ < 0:
neg.append(_) # 角度为正
else:
pos.append(_) # 角度为负
notmaxnumber = len(neg)+len(pos)
if notmaxnumber == 4 or notmaxnumber == 3: # 非垂直的直线个数为3或4
"""
如果角度为负和角度为正的直线哪个组直线个数多,那么就计算组内直线的角度均值,作为手掌中线角度;
如果个数相等,则计算两组的角度和的绝对值,绝对值大的组内直线的角的均值作为手掌中线角度;
如果绝对值相等,那么直接将手掌中线角度设置为pi/2,也就是MAXANGLE
"""
if len(neg) > len(pos):
averageangle = sum(neg) / len(neg)
elif len(neg) < len(pos):
averageangle = sum(pos) / len(pos)
elif fabs(sum(neg)) > fabs(sum(pos)):
averageangle = sum(neg) / len(neg)
elif fabs(sum(neg)) < fabs(sum(pos)):
averageangle = sum(pos) / len(pos)
else:
averageangle = MAXANGLE
elif notmaxnumber == 2:
"""
如果只存在两条非垂直直线,则计算两条直线的角度与MAXANGLE计算均值
从实际意义出发,因为存在两个中指骨骼点与掌心骨骼点构成的直线竖直,所以垂直角度(即pi/2)也应该占据一定的权重;
从计算的角度出发,如果一条非垂直直线的角度为-x,另一条非垂直直线的角度为x,则若不考虑pi/2,则二者计算均值为0,这显然与预期角度不符,
而加上pi/2之后就很好地解决了该问题
"""
averageangle = (MAXANGLE + sum(neg) + sum(pos)) / (len(neg) + len(pos) + 1)
else:
"""
由于垂直直线比较多,说明矩形框竖直的可能性比较大,所以直接设置为最大角度
"""
averageangle = MAXANGLE # ≈ pi/2
x, y = lms[0]
k = tan(averageangle)
b = y - k * x
return (k, b)
def pointtopointdistance(p1, p2):
"""
点到点的距离
:param p1: 一个元组,包含横坐标和纵坐标
:param p2: 一个元组,包含横坐标和纵坐标
:return: 浮点数,距离
"""
x1, y1 = p1
x2, y2 = p2
return sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)
def pointtolinedistance(p, l, absolute=False):
"""
点到直线的”距离“
注意:如果不取绝对值,则可以判断点位于直线的哪一侧
:param p: 一个元组,包含横坐标和纵坐标
:param l: 一个元组,包含斜率和截距
:param absolute: 布尔类型,距离是否取绝对值
:return: 点到直线的”距离“
"""
x, y = p
k, b = l
return (abs(k * x + b - y) if absolute else k * x + b - y) / (k ** 2 + 1)
def pointwithdistance(lms, line):
"""
与掌心骨骼点距离为d,位于以斜率均值为斜率且过掌心骨骼点的直线上的点的坐标
联立公式:
y = k*x+b
d^2 = (x-x0)^2 + (y-y0)^2
最后采用求根公式
:param lms: 21个关键点(骨骼点)
:param line: 一个元组,包含斜率和截距
:return: 所求点的坐标,一个元组,包含横坐标和纵坐标
"""
d = 0 # 中指骨骼点、手掌点之间的距离和
for idx in range(9, 13, 1):
d += pointtopointdistance(lms[idx], lms[0 if idx is 9 else idx - 1])
print(d)
cx, cy = lms[0]
k, b = line
aa = k ** 2 + 1 # 注意^表示按位异或,**表示幂乘
bb = 2 * (k * b - k * cy - cx)
cc = cx ** 2 + (b - cy) ** 2 - d ** 2
det = bb ** 2 - 4 * aa * cc
x1 = (-bb + sqrt(det)) / (2 * aa)
y1 = k * x1 + b
x2 = (-bb - sqrt(det)) / (2 * aa)
y2 = k * x2 + b
p1 = (int(x1), int(y1)) # 注意转换为整数
p2 = (int(x2), int(y2)) # 注意转换为整数
return p1 if pointtopointdistance(p1, lms[12]) < pointtopointdistance(p2, lms[12]) else p2 # 距离标记点12近的为答案
def getlinebais(p, k):
"""
已知点坐标和直线斜率,求确定的直线截距
:param p: 一个元组,包含横坐标和纵坐标
:param k: 直线斜率
:return: 截距
"""
x, y = p
return y - k * x
def intersectionpoint(l1, l2):
"""
已知两条直线,求交点坐标
:param l1: 一个元组,包含斜率和截距
:param l2: 一个元组,包含斜率和截距
:return: 一个元组,包含横坐标和纵坐标
"""
k1, b1 = l1
k2, b2 = l2
return ((b1 - b2) / (k2 - k1), (k2 * b1 - k1 * b2) / (k2 - k1))
def findcontours(lms, toppoint, middleline):
"""
确定矩形的四个点
:param lms: 21个关键点
:param toppoint: 已经求出的与掌心骨骼点距离为d的点
:param middleline: 手掌中线,一个元组,包含斜率和截距
:return: 包含四个坐标(元组)的列表
"""
leftpoint = rightpoint = lms[0]
leftdist = rightdist = 0
for p in lms:
dist = pointtolinedistance(p, middleline)
if dist < leftdist:
leftpoint = p
leftdist = dist
elif dist > rightdist:
rightpoint = p
rightdist = dist
lines = []
k, b = middleline
# print(k)
lines.append((-1.0/k, getlinebais(toppoint, -1.0/k)))
lines.append((k, getlinebais(leftpoint, k)))
lines.append((-1.0/k, getlinebais(lms[0], -1.0/k)))
lines.append((k, getlinebais(rightpoint, k)))
contours = []
for i in range(len(lines)):
contours.append(intersectionpoint(lines[i], lines[-1] if i is 0 else lines[i-1]))
return contours
def crophand(frame, lms):
middleline = averageline(lms)
toppoint = pointwithdistance(lms, middleline)
cv2.circle(frame, toppoint, 7, (255, 0, 0), cv2.FILLED) # 确定的上边界点
contours = findcontours(lms, toppoint, middleline)
contours = np.array(contours, dtype=np.int) # 转为int
for x, y in contours:
cv2.circle(frame, (x, y), 7, (255, 0, 0), cv2.FILLED)
for i in range(len(contours)):
cv2.line(frame, contours[i], contours[-1] if i is 0 else contours[i-1], (0, 0, 255), 2)
# 无需绘制最小外接矩形,因为算出来的就是个矩形,直接画直线即可
# rect = cv2.minAreaRect(np.array(contours, dtype=np.int)) # 注意转换为整数
# points = np.int0(cv2.boxPoints(rect)) # 得到最小外接矩形的四个点坐标
# cv2.drawContours(frame, [points], 0, (0, 0, 255), 2) # 直接在原图上绘制矩形框
# plotinfinitystones(frame, lms) # 无限宝石!
def plotinfinitystones(frame, lms):
"""
!!!慎重调用该函数,可能导致地球一半的人消失!!!
"""
# 0:黄 2:绿 5:粉 9:蓝 13:红 17:橙
d = pointtopointdistance(lms[0], lms[9])
bigstonesize = (d/3.8, d/4)
smallstonesize = (d/6.3, d/7)
x, y = lms[0]
y -= d/3.5
points = np.array([[x, y-bigstonesize[0]], [x+bigstonesize[1]/2, y-bigstonesize[0]/2], [x+bigstonesize[1]/2, y+bigstonesize[0]/2], [x, y+bigstonesize[0]], [x-bigstonesize[1]/2, y+bigstonesize[0]/2], [x-bigstonesize[1]/2, y-bigstonesize[0]/2]], dtype=np.int)
cv2.fillConvexPoly(frame, points, (24,255,255))
# 2:绿
x, y = lms[2]
points = np.array([[x, y - smallstonesize[0]], [x + smallstonesize[1] / 2, y - smallstonesize[0] / 2], [x + smallstonesize[1] / 2, y + smallstonesize[0] / 2], [x, y + smallstonesize[0]], [x - smallstonesize[1] / 2, y + smallstonesize[0] / 2], [x - smallstonesize[1] / 2, y - smallstonesize[0] / 2]], dtype=np.int)
cv2.fillConvexPoly(frame, points, (120, 255, 40))
# 5:粉
x, y = lms[5]
points = np.array([[x, y - smallstonesize[0]], [x + smallstonesize[1] / 2, y - smallstonesize[0] / 2],
[x + smallstonesize[1] / 2, y + smallstonesize[0] / 2], [x, y + smallstonesize[0]],
[x - smallstonesize[1] / 2, y + smallstonesize[0] / 2],
[x - smallstonesize[1] / 2, y - smallstonesize[0] / 2]], dtype=np.int)
cv2.fillConvexPoly(frame, points, (240, 60, 209))
# 9:蓝
x, y = lms[9]
points = np.array([[x, y - smallstonesize[0]], [x + smallstonesize[1] / 2, y - smallstonesize[0] / 2],
[x + smallstonesize[1] / 2, y + smallstonesize[0] / 2], [x, y + smallstonesize[0]],
[x - smallstonesize[1] / 2, y + smallstonesize[0] / 2],
[x - smallstonesize[1] / 2, y - smallstonesize[0] / 2]], dtype=np.int)
cv2.fillConvexPoly(frame, points, (240, 230, 50))
# 13:红
x, y = lms[13]
points = np.array([[x, y - smallstonesize[0]], [x + smallstonesize[1] / 2, y - smallstonesize[0] / 2],
[x + smallstonesize[1] / 2, y + smallstonesize[0] / 2], [x, y + smallstonesize[0]],
[x - smallstonesize[1] / 2, y + smallstonesize[0] / 2],
[x - smallstonesize[1] / 2, y - smallstonesize[0] / 2]], dtype=np.int)
cv2.fillConvexPoly(frame, points, (37, 15, 240))
# 17:橙
x, y = lms[17]
points = np.array([[x, y - smallstonesize[0]], [x + smallstonesize[1] / 2, y - smallstonesize[0] / 2],
[x + smallstonesize[1] / 2, y + smallstonesize[0] / 2], [x, y + smallstonesize[0]],
[x - smallstonesize[1] / 2, y + smallstonesize[0] / 2],
[x - smallstonesize[1] / 2, y - smallstonesize[0] / 2]], dtype=np.int)
cv2.fillConvexPoly(frame, points, (44, 160, 255))
houghcircle.py
"""
作者:LJR
日期:2022 06 27
"""
import cv2
import numpy as np
def houghcircle(frame):
"""
返回参照圆的半径(像素)
注意返回值!
:param frame: 图像
:return: 如果检测到圆,则半径;否则返回None。
"""
cropped_frame = frame[250:450, 200:450]
# 对滤波结果做边缘检测获取目标
cropped_frame = cv2.Canny(cropped_frame, 50, 150)
# 使用膨胀和腐蚀操作进行闭合对象边缘之间的间隙
cropped_frame = cv2.dilate(cropped_frame, None, iterations=1)
cropped_frame = cv2.erode(cropped_frame, None, iterations=1)
# 霍夫变换圆检测
circles = cv2.HoughCircles(cropped_frame, cv2.HOUGH_GRADIENT, 1, 200,
param1=200, param2=20, minRadius=20, maxRadius=100)
# if circles is not None:
# circles = np.uint16(np.around(circles))
# cv2.circle(cropped_frame, (circles[0][0][0], circles[0][0][1]), circles[0][0][2], 50, 3)
cv2.imshow("Hough Circles", cropped_frame) # 如果programentry中的全部measureXXXX函数都被注释掉,则不会显示裁剪出的圆
return circles[0][0].flatten()[-1] if circles is not None else None
measureanglebetweenfingers.py
"""
作者:LJR
日期:2022 06 27
"""
import numpy as np
from houghcircle import houghcircle
FINGERS_NAME = ['thumb', 'index', 'middle', 'ring', 'little']
def measureanglebetweenfingers(handedge, handmask, lms, fingermaskandlms):
_, _, finger_theta = fingermaskandlms # 三个 numpy
convert_theta = [i-360 if 360-i < i else i for i in finger_theta] # 将 35X 的度数转换为 35X-360,其他的不变,之后相邻两个计算差值的绝对值就是夹角
# 判断是否需要变换并不是看数是否为35X,而是看 360-degree和degree的大小关系,360-degree小说明需要变换
degrees = np.abs(np.diff(convert_theta))
for i in range(4):
print('The degree between ' + FINGERS_NAME[i] + ' and ' + FINGERS_NAME[i+1] + ' is ' + str(np.round(degrees[i], 2)) + '°')
print('--------------------------------------------------')
measurefingerslengthwidth.py
"""
作者:LJR
日期:2022 05 21
"""
import cv2
import numpy as np
from plotfigure import *
from houghcircle import houghcircle
FINGERS_NAME = ['thumb', 'index', 'middle', 'ring', 'little']
CION_RADIUS = 10 # 10 mm # 固定长度
def measurefingerswidth(fingermaskandlms, radius):
"""
计算手指宽度
实现思路:对被裁剪出的每根手指的图像进行竖直方向的投影,对应于代码中的竖直方向上的计算累积值。
将每根手指的每个骨骼点所在水平线上侧的图像部分投影到该直线上,对应于代码中的取累积值矩阵的水平线所在的行。
确定一个阈值后,每个水平线上的投影根据累积值确定手指的宽度像素,最后根据比例转换成实际长度即可。
:param fingermaskandlms:
:param radius:
:return:
"""
finger_mask, finger_lms, _ = fingermaskandlms # 两个 numpy
for i in range(len(finger_lms)): # 五根手指
fingerframe = finger_mask[i]
fingername = FINGERS_NAME[i]
fingerlms = finger_lms[i]
# 原lm是按照骨骼点编号从小到大排序的,现在改为从上到下,即从指尖向下
# 最下面的骨骼点(每根手指的第四个点,编号最小的骨骼点)在多数情况下,是不会显示在图像中的,因此不考虑该点
fingerlms = fingerlms[::-1][:-1]
# 向下按顺序计算累积和(前缀和),相当于在竖直方向上投影
# 计算的是为255的数量,即白点的数量,而不是单纯的累积值
accumulatesum = np.cumsum(fingerframe != 0, axis=0)
knucklewidth = [] # 每个指关节的宽度
for j in range(len(fingerlms)): # 每根手指上的上三个骨骼点
lm = fingerlms[j]
x, y = lm # 注意lm是(x,y),而图像是(row,col),二者正好相反
cum_list = accumulatesum[y][:]
# 绘制掩膜累积图
# plotMaskCumulativeGraph(cum_list, fingername + '_' + str(j+1))
threshold = 0.2 * np.max(cum_list) # 当累积值非0的个数大于阈值时才被视为是手指
# 注意我们的阈值不是与从上到下的长度有关而是与累计值中的最大值成比例
cum_list_boolean = cum_list > threshold # 根据阈值转换为布尔类型
width = 0 # 每个指关节的宽度
for k in np.linspace(1, len(cum_list), 10)[1:-1]: # 枚举分界线位置,分界线向左找0,分界线向右找0
k = int(k)
try: # 鲁莽地处理一下异常
left = np.where(cum_list_boolean[:k] == False)[0][-1] + 1 # 分界线左边最靠近分界线的0
right = k + np.where(cum_list_boolean[k - 1:] == False)[0][0] - 1 # 分界线右边最靠近分界线的0
width = max(width, right - left) # 全部枚举方案得到的最大的手指宽度为最终结果
except IndexError:
print('IndexError')
knucklewidth.append(np.round(CION_RADIUS * width / radius, 2)) # 转换为实际长度并保留两位小数
# print(fingername + '_' + str(j+1), str(width) + 'px', str(np.round(CION_RADIUS * width / radius, 2)) + 'mm')
# 最上面的指关节的参考价值不高,因为该骨骼点有时会很靠上,导致计算的长度非常小
print('The width of %s is' % (fingername), knucklewidth)
def measurefingerslength(fingermaskandlms, radius):
"""
计算手指长度
实现思路:对于非大拇指的手指,直接计算四个骨骼点距离和;对于大拇指计算前三个骨骼点距离和
:param fingermaskandlms:
:param radius:
:return:
"""
finger_mask, finger_lms, _ = fingermaskandlms # 两个 numpy
length_list = []
for i in range(len(finger_lms)): # 五根手指
fingername = FINGERS_NAME[i]
fingerlms = finger_lms[i]
lengthpx = np.sum(np.sqrt(np.sum(np.diff(fingerlms[:-1] if i is 0 else fingerlms, axis=0) ** 2, axis=1)), axis=0)
# print('The length of %s is' % (fingername), np.round(lengthpx * CION_RADIUS / radius, 2))
length_list.append(np.round(lengthpx * CION_RADIUS / radius, 2))
print('The length of each finger is', length_list)
def measurefingerslengthwidth(frameedge, framemask, lms, fingermaskandlms):
"""
计算每根手指的长度和宽度并输出
:param frame: 黑白掩模图
:param lms: 关键点坐标
:param fingermaskandlms: 手指掩模图和对应的骨骼点(一个元组,第一个元素为每个手指的mask,第二个元素为)
:return: 无
"""
"""
# 被抛弃的思路:计算出handedge中每个白色像素到骨骼点的最短距离,乘以2作为手指宽度。
# 显然,当距离骨骼点最近的白色像素点不是手指侧边的像素值时,计算结果与预期不符;另外不能保证骨骼点一定位于手指中线上,因此乘以2的思路也不合适。
row_edge, col_edge = np.where(frameedge != 0)# 第一个是行,第二个是列 # 6000
row_mask, col_mask = np.where(framemask != 0) # 100000
edge = np.squeeze(np.dstack((row_edge, col_edge))) # 一个二维ndarray,每个元素是一个坐标
lms = np.array(lms) # 转为ndarray类型
dists = np.sqrt(np.sum((edge - lms[8]) ** 2, axis=1)) # 每个手掌边界点到某个骨骼点的距离
print(edge[np.argmin(dists)])
"""
radius = houghcircle(frameedge)
# 注意可能返回None!!!
if radius is None:
print('【ERROR】 Not Find Reference Circle !') # 最终可以将输出去掉!
return None
measurefingerswidth(fingermaskandlms, radius)
measurefingerslength(fingermaskandlms, radius)
print('---------------------Unit: mm---------------------')
measurepalmandwristwidth.py
"""
作者:LJR
日期:2022 05 21
"""
import cv2
import numpy as np
from math import *
import matplotlib.pyplot as plt
from houghcircle import houghcircle
from sklearn.preprocessing import StandardScaler as SS
from sklearn.linear_model import LinearRegression as LR
CION_RADIUS = 10 # 10 mm # 固定长度
def residualanalysis(y, y_hat):
"""
确定非离群点。
先计算每个数据的标准化残差,对于大于3 sigma的数据,我们视为离群点。
【效果不佳,不采用!】
:param y: 观测值
:param y_hat: 预测值
:return: 布尔数组和标准化残差
"""
y, y_hat = np.array(y), np.array(y_hat)
y_residual = y - y_hat
y_residual_average = y_residual / len(y_residual)
y_standarized_residual = y_residual / np.sqrt((y_residual - y_residual_average) ** 2 / len(y_residual))
# 返回一个布尔数组,False表示对应位置为离群点
return np.bitwise_and(y_standarized_residual > -3, y_standarized_residual < 3), y_standarized_residual
# numpy两个布尔数组不能用and或or,需要用固定的np函数
def measurewristwidth(frameedge, lms, radius):
"""
计算手腕宽度。
实现思路:0号关键点下面的部分视为手腕。
将手腕部分handedge的最左侧白色点集合,最右侧白色点集合,两个集合维数是相同的,对应位置表示的是一个水平线上手腕两端的边界。
(对于同一侧的点集进行残差分析,剔除偏离较大的点),通过剩下的点确定两侧的直线斜率,计算两条直线的斜率均值。
以斜率均值作为两侧新的直线的斜率,以剩下的点集中位于中间位置的点分别作为两侧新的直线经过的点,如此可以确定两条平行的直线。
计算两条平行直线的距离作为手腕宽度。
(发现残差分析效果不佳,几乎所有的点都处于 3 sigma 之外了,所以都被视为离群点了,与预期严重不符)
:param frameedge:
:param lms:
:param radius:
:return:
"""
_, top_y = lms[0]
bottom_y, _ = frameedge.shape
# 需要以图像的行(同y坐标)为自变量,以图像的列(同x坐标)为因变量。因为如果反过来,则可能存在一个自变量对应多个因变量的情况。
x_range = []
left_y_range = []
right_y_range = []
for y in np.arange(int(top_y + 0.2 * (bottom_y - top_y)), bottom_y, 1):
p = np.where(frameedge[y] != 0)[0]
if len(p) >= 2:
x_range.append(y)
left_y_range.append(p[0])
right_y_range.append(p[-1])
x_range = np.array(x_range).reshape(-1, 1)
left_y_range = np.array(left_y_range).reshape(-1, 1)
right_y_range = np.array(right_y_range).reshape(-1, 1)
# left_y_range = SS().fit_transform(left_y_range)
# right_y_range = SS().fit_transform(right_y_range)
if len(x_range) == 0: # 不存在手腕部分,防止下面出现异常,所以直接return
return None
# 一元线性回归,确定手腕两侧直线方程
model_left = LR().fit(x_range, left_y_range)
model_right = LR().fit(x_range, right_y_range)
# 预测值
left_y_pre = model_left.predict(x_range)
right_y_pre = model_right.predict(x_range)
"""
# 残差分析效果不好
left_boolean, left_residual = residualanalysis(left_y_range, left_y_pre)
right_boolean, right_residual = residualanalysis(right_y_range, right_y_pre)
print(left_boolean)
left_y_notoutliers = left_y_range[left_boolean]
right_y_notoutliers = right_y_range[right_boolean]
print(len(left_y_range), len(left_y_notoutliers))
plt.plot(x_range, right_y_range, 'o')
# plt.plot(x_range, left_y_range, 'p')
plt.show()
plt.figure()
plt.plot(x_range, np.zeros_like(x_range), '--g')
plt.plot(x_range, 2 * np.ones_like(x_range), '--r', x_range, -2 * np.ones_like(x_range), '--r')
boolean, y_pre = residualanalysis(left_y_range, model_left.predict(x_range))
plt.plot(x_range, y_pre, 'o')
plt.show()
"""
# 预测的直线
# plt.plot(x_range, left_y_range, 'o', x_range, right_y_range, 'o')
# plt.plot(x_range, left_y_pre, '--', x_range, right_y_pre, '--')
# plt.show()
# 斜率与截距
left_k, right_k = model_left.coef_, model_right.coef_
# left_b, right_b = model_left.intercept_, model_right.intercept_ # 截距信息用不到
average_k = (left_k + right_k) / 2 # 两侧直线斜率均值
# ”中心“的点,只是找x的中位数和两个y的中位数,作为”中心“的点,但其实该点并不位于手腕边界
mid_x = np.median(x_range)
left_mid_y, right_mid_y = np.median(left_y_range, axis=0), np.median(right_y_range, axis=0)
# 计算以均值斜率作为手腕两侧斜率的直线,过上面两个中心点的直线截距
b1, b2 = left_mid_y - average_k * mid_x, right_mid_y - average_k * mid_x
# 计算两直线距离
distancebetweenlines = abs(b1 - b2) / sqrt(average_k ** 2 + 1)
print('The width of wrist is', np.round(distancebetweenlines[0][0] * CION_RADIUS / radius, 2))
def measurepalmwidth(framemask, lms, radius):
"""
计算两个宽度。
第一个是四个手指对应的手掌宽度,第二个是五根手指对应的宽度。
Case1:确定上下左右的边界,将矩形框内的部分裁剪出来,水平方向累积投影,取累积值的中位数作为手掌宽度
核心在于确定上下左右边界。先确定水平中线,为lms[5, 9, 13, 17].y 的均值;
上下边界是通过水平中线位置分别向上向下偏移一定的距离来确定,偏移量为 1/4 的非大拇指的四个手指的最长指关节(即最下面的)长度的均值;
左边界为lms[2].x;(大拇指向外撇的程度小时,会存在将部分大拇指裁剪进来的情况,更准确的做法可以是从中心垂线向两侧找第一个黑像素,两个黑像素距离差值就是宽度)
右边界为lms[9] 关于 lms[17] 的对称点的x坐标。
之所以不采用直接裁剪出小拇指向右的全部像素,是因为小拇指不一定位于手的右侧,
如果将手掌翻面,则小手指位于手的左侧,而采用对称点就不用考虑左右了。
Case2:骨骼点2所在水平线的像素向竖直方向投影就是五根手指对应的手掌宽度。这里不采用五根手指的宽度进行累加,因为本身计算出的手指宽度就存在误差,将存在误差的数据累加会放大误差。
注意,由于掌心会存在一个黑色的圆,会影响最终的计算结果,所以需要变换一下思路。
找到水平线上最左边的白像素和最右边的白像素之间的距离作为结果(这种算法需要保证手掌掩膜比较理想,不能存在噪声点)
:param framemask:
:param lms:
:param radius:
:return:
"""
# lms[5, 9, 13, 17].y 的均值
mid = np.mean([lms[i][1] for i in np.linspace(5, 17, 4, dtype=np.int)])
# 一句话秒杀,太帅了。计算lms:5和6,9和10,13和14,17和18的距离和均值
inc = 0.25 * np.mean([np.sqrt(np.sum(np.diff(np.array([lms[i], lms[i + 1]]), axis=0) ** 2, axis=1))[0]
for i in np.linspace(5, 17, 4, dtype=np.int)])
top = mid - inc
down = mid + inc
# lms[2].x
left = lms[2][0]
# lms[9] 关于 lms[17] 的对称点的x坐标作为 right(裁剪区域的右边界)
right = 2 * lms[17][0] - lms[9][0]
# 注意刚计算出来的left和right并不一定代表左右边界(手掌反过来),所以需要根据大小判断是否交换值
if left > right:
_ = left
left = right
right = _
_ = framemask[int(top):int(down), int(left):int(right)]
# cv2.imshow('For Palm Width', _)
palmwidthpx_1 = np.median(np.sum(_ != 0, axis=1))
print('The width of palm is', np.round(palmwidthpx_1 * CION_RADIUS / radius, 2), '(case 1)')
_ = np.where(framemask[lms[2][1]] != 0)[0]
if len(_) >= 2: # 防止报错
palmwidthpx_2 = _[-1] - _[0]
else:
print('【ERROR】Case 2')
return
print('The width of palm is', np.round(palmwidthpx_2 * CION_RADIUS / radius, 2), '(case 2)')
def measurepalmandwristwidth(frameedge, framemask, lms):
"""
计算手掌宽度和手腕宽度并输出
:param frame: 黑白掩模图
:param lms: 关键点坐标
:return: 无
"""
radius = houghcircle(frameedge)
# 注意可能返回None!!!
if radius is None:
print('【ERROR】 Not Find Reference Circle !') # 最终可以将输出去掉!
return None
measurewristwidth(frameedge, lms, radius)
measurepalmwidth(framemask, lms, radius)
print('---------------------Unit: mm---------------------')
plotfigure.py
"""
作者:LJR
日期:2022 06 28
"""
import numpy as np
import matplotlib.pyplot as plt
def plotMaskCumulativeGraph(cum_list, graph_name):
"""
绘制(或保存)每根手指的每个指关节的所在水平线上的投影累积图
:param cum_list:
:param graph_name:
:return:
"""
x = np.arange(len(cum_list))
fig, ax = plt.subplots()
plt.xticks([])
plt.yticks([])
ax.fill(x, cum_list, color='black')
# fig.suptitle(graph_name)
plt.savefig('./pic/' + graph_name + '.png') # 保存累积图,如果在识别手掌的时候进行会非常卡,因此仅用于观察和写实验报告
# plt.show()
"""
显示保存的图片
"""
"""
PATH = './pic/'
idx = 0
for i in [1, 2, 3]:
for name in ['thumb', 'index', 'middle', 'ring', 'little']:
idx += 1
plt.subplot(3, 5, idx)
plt.xticks([])
plt.yticks([])
img = plt.imread(PATH + name + '_' + str(i) + '.png')
if i == 1:
plt.title(name)
plt.imshow(img)
plt.tight_layout() # 每个子图大点,缝隙小点
plt.show()
"""
minAreaRect_to_get_whole_palm.py
"""
作者:LJR
日期:2022 05 17
"""
"""
被抛弃的方案
"""
import cv2
import numpy as np
import mediapipe as mp
mp_drawing = mp.solutions.drawing_utils
mp_hands = mp.solutions.hands
hands = mp_hands.Hands(
static_image_mode=False,
max_num_hands=2,
min_detection_confidence=0.75,
min_tracking_confidence=0.75)
cap = cv2.VideoCapture(0, cv2.CAP_DSHOW)
while True:
ret, frame = cap.read()
H, W, C = frame.shape
frame = cv2.cvtColor(frame, cv2.COLOR_BGR2RGB)
frame= cv2.flip(frame,1) # 镜像翻转
results = hands.process(frame)
frame = cv2.cvtColor(frame, cv2.COLOR_RGB2BGR)
if results.multi_handedness:
for hand_label in results.multi_handedness:
print(hand_label)
if results.multi_hand_landmarks:
for hand_landmarks in results.multi_hand_landmarks:
# 关键点可视化
mp_drawing.draw_landmarks(
frame, hand_landmarks, mp_hands.HAND_CONNECTIONS)
contours = []
for landmarks in hand_landmarks.landmark:
pos_x, pos_y = int(landmarks.x * W), int(landmarks.y * H) # 图像中的坐标
contours.append([pos_x, pos_y])
rect = cv2.minAreaRect(np.array(contours))
points = np.int0(cv2.boxPoints(rect)) # 得到最小外接矩形的四个点坐标
cv2.drawContours(frame, [points], 0, (0, 0, 255), 2) # 直接在原图上绘制矩形框
cv2.imshow('MediaPipe Hands', frame)
if cv2.waitKey(1) & 0xFF == 27:
break
cap.release()