【XGBoost】第 3 章：随机森林装袋

     大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流

个人主页－Sonhhxg_柒的博客_CSDN博客 

欢迎各位→点赞 + 收藏⭐️ + 留言​

系列专栏 - 机器学习【ML】 自然语言处理【NLP】  深度学习【DL】

​

 foreword

✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

如果你对这个系列感兴趣的话，可以关注订阅哟

文章目录

装袋集成

集成方法

引导聚合

探索随机森林

随机森林分类器

随机森林回归器

随机森林超参数

oob_score

n_estimators

warm_start

bootstrap

Verbose

决策树超参数

Depth

Splits

Leaves

推动随机森林边界——案例研究

准备数据集

n_estimators

cross_val_score

微调超参数

随机森林的缺点

概括

---

在本章中，您将精通构建随机森林，这是 XGBoost 的主要竞争对手。与 XGBoost 一样，随机森林是决策树的集合。不同之处在于随机森林通过bagging组合树，而 XGBoost 通过boosting组合树。随机森林是 XGBoost 的可行替代方案，其优点和局限性将在本章中重点介绍。了解随机森林很重要，因为它们为基于树的集成 (XGBoost) 的结构提供了有价值的见解，并且通过与他们自己的 bagging 方法进行比较和对比，它们可以更深入地理解提升。

在本章中，您将构建和评估随机森林分类器和随机森林回归器，掌握随机森林超参数，了解机器学习领域中的 bagging，并探索一个案例研究，该案例研究突出了促进梯度发展的一些随机森林限制提升（XGBoost）。

本章涵盖以下主要主题：

• 装袋集成

• 探索随机森林

• 调整随机森林超参数

• 推动随机森林边界——案例研究

装袋集成

在本节中，您将了解为什么集成方法通常优于单个机器学习模型。此外，您将了解装袋技术。两者都是随机森林的基本特征。

集成方法

在机器学习中，集成方法是一种机器学习模型，它聚合了个别型号。由于集成方法结合了多个模型的结果，因此它们不太容易出错，因此往往表现更好。

想象一下，您的目标是确定房屋是否会在上市后的第一个月内出售。您运行了几种机器学习算法，发现逻辑回归的准确率为 80%，决策树的准确率为 75%，k 最近邻的准确率为 77%。

一种选择是使用最准确的逻辑回归模型作为最终模型。一个更有说服力的选择是结合每个单独模型的预测。

对于分类器，标准选项是获得多数票。如果三个模型中至少有两个预测房屋将在第一个月内出售，则预测为YES。否则，它是NO。

集成方法的总体准确度通常更高。对于一个错误的预测，仅仅一个模型会出错是不够的；大多数分类器肯定弄错了。

集成方法通常分为两种类型。第一种类型结合了用户选择的不同机器学习模型，例如 scikit-learn 的VotingClassifier。第二种类型的集成方法结合了同一模型的多个版本，例如 XGBoost 和随机森林。

随机森林是所有集成方法中最流行和最广泛的方法之一。随机森林的各个模型是决策树，上一章的重点，第 2章，Deepth 的决策树。一个随机森林可能由成百上千个决策树组成，它们的预测被组合起来以获得最终结果。

尽管随机森林对分类器使用多数规则，对回归器使用所有模型的平均值，但它们也使用称为 bagging 的特殊方法，是 bootstrap 聚合的缩写，用于选择单个树。

引导聚合

自举方式更换取样。

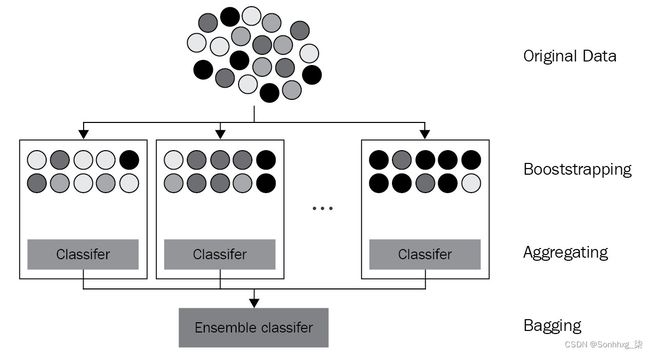
想象一下，你有一袋 20 颗带阴影的弹珠。您将选择 10 个弹珠，一次选择一个。每次你选择一个弹珠，你就把它放回袋子里。这意味着您有可能（尽管可能性极小）挑选同一个大理石 10 次。

更有可能是你会不止一次地挑选一些弹珠，而有些则根本不会。

这是弹珠的视觉效果：

 

图 3.1 – bagging 的可视化演示（重绘自：Siakorn, Wikimedia Commons, https://commons.wikimedia.org/wiki/File:Ensemble_Bagging.svg）

从上图中可以看出，bootstrap 样本是通过带放回抽样来实现的。如果不更换弹珠，就不可能获得比原始袋子更多的黑色（原图中蓝色）弹珠的样品，如最右边的方框所示。

当涉及到随机森林时，自举在幕后工作。引导发生在每个决策树生成时。如果决策树都由相同的样本组成，那么这些树会给出相似的预测，从而使聚合结果类似于单个树。相反，对于随机森林，树是使用引导构建的，通常使用与原始数据集中相同数量的样本。数学估计是每棵树的三分之二样本是唯一的，三分之一包括重复。

在模型构建的引导阶段之后，每个决策树都会做出自己的预测。这结果是一片树的森林，其预测被聚合成一个最终预测，使用分类器的多数规则和回归器的平均值。

总之，随机森林聚合了自举决策树的预测。这种通用集成方法在机器学习中称为 bagging。

探索随机森林

为了更好地了解随机森林是如何工作的，让我们使用 scikit-learn 构建一个。

随机森林分类器

让我们使用随机森林分类器来预测用户使用人口普查的收入是多于还是少于 50,000 美元我们在第 1 章“机器学习领域”中清理和评分的数据集，并在第 2 章“深度决策树”中重新访问。我们将使用cross_val_score来确保我们的测试结果很好地概括：

以下步骤使用人口普查数据集构建和评分随机森林分类器：

1. 在消除警告之前导入pandas、numpy、RandomForestClassifier和cross_val_score：

   import pandas as pd
   import numpy as np
   from sklearn.ensemble import RandomForestClassifier
   from sklearn.model_selection import cross_val_score
   import warnings
   warnings.filterwarnings('ignore')

2. 加载数据集census_cleaned.csv并将其拆分为X（预测列）和y（目标列）：

   df_census = pd.read_csv('census_cleaned.csv')
   X_census = df_census.iloc[:,:-1]
   y_census = df_census.iloc[:,-1]

   随着我们的导入和数据准备就绪，是时候构建模型了。

3. 接下来，我们初始化随机森林分类器。在实践中，集成算法就像任何其他机器学习算法一样工作。模型被初始化，适合训练数据，并且对测试数据进行评分。

   我们通过预先设置以下超参数来初始化随机森林：

   a) random_state=2以确保您的结果与我们的一致。

   b) n_jobs=-1通过利用并行处理来加速计算。

   c) n_estimators=10，先前的 scikit-learn 默认值足以加速计算并避免歧义；新的默认设置为 n_estimators=100。n_esmitators将在下一节中更详细地探讨：

   rf = RandomForestClassifier(n_estimators=10, random_state=2, n_jobs=-1)

4. 现在我们将使用cross_val_score。Cross_val_score需要模型、预测列和目标列作为输入。回想一下cross_val_score对数据的拆分、拟合和评分：

   scores = cross_val_score(rf, X_census, y_census, cv=5)

5. 显示结果：

   print('Accuracy:', np.round(scores, 3))
   print('Accuracy mean: %0.3f' % (scores.mean()))
   
   # Accuracy: [0.851 0.844 0.851 0.852 0.851]
   # Accuracy mean: 0.850

默认随机森林分类器为人口普查数据集提供了比第 2 章深度决策树中的决策树（81%）更好的分数，但不如第 1 章机器学习景观中的 XGBoost （86%）好。为什么它比单个决策树表现更好？

改进的性能可能是由于上一节中描述的 bagging 方法。在这片森林中有 10 棵树（因为n_estimators=10），每个预测都基于 10 棵决策树而不是 1 棵。这些树是自举的，这增加了多样性，并聚合了，这减少了方差。

默认情况下，随机森林分类器在查找时从特征总数的平方根中选择分裂。所以，如果有 100 个特征（列），每个决策树在选择拆分时只会考虑 10 个特征。因此，由于不同的拆分，具有重复样本的两棵树可能会给出非常不同的预测。这是随机森林减少方差的另一种方式。

除了分类之外，随机森林也适用于回归。

随机森林回归器

在随机森林回归器中，样本是自举的，与随机森林分类器一样，但最大特征数是特征总数而不是平方根。这种变化是由于实验结果（见https://orbi.uliege.be/bitstream/2268/9357/1/geurts-mlj-advance.pdf）。

此外，最终预测是通过取所有树的预测的平均值来做出的，而不是多数规则投票。

要查看运行中的随机森林回归器，请完成以下步骤：

1. 上传第 2 章“深度决策树”中的自行车租赁数据集，并拉出前五行进行复习：

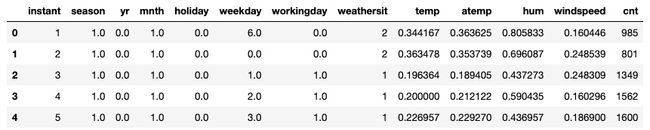
   df_bikes = pd.read_csv('bike_rentals_cleaned.csv')
   df_bikes.head()

   上述代码应产生以下输出：

   

   图 3.2 – 自行车租赁数据集 – 已清理

2. 将数据拆分为X和y、预测列和目标列：

   X_bikes = df_bikes.iloc[:,:-1]
   y_bikes = df_bikes.iloc[:,-1]

3. 导入回归器，然后使用相同的默认超参数n_estimators=10、random_state=2和n_jobs=-1对其进行初始化：

   from sklearn.ensemble import RandomForestRegressor
   rf = RandomForestRegressor(n_estimators=10, random_state=2, n_jobs=-1)

4. 现在我们需要使用cross_val_score。将回归器rf以及预测器和目标列放在cross_val_score中。请注意，负均方误差 ( 'neg_mean_squared_error' ) 应定义为评分参数。选择 10 折（cv=10）：

   scores = cross_val_score(rf, X_bikes, y_bikes, scoring='neg_mean_squared_error', cv=10)

5. 寻找并显示均方根误差( RMSE )：

   rmse = np.sqrt(-scores)
   print('RMSE:', np.round(rmse, 3))
   print('RMSE mean: %0.3f' % (rmse.mean()))

   输出如下：

   RMSE: [ 801.486  579.987  551.347  846.698  895.05  1097.522   893.738  809.284  833.488 2145.046]
   
   RMSE mean: 945.365

随机森林的表现可观，尽管不如我们见过的其他模型。我们将在本章后面的案例研究中进一步检查自行车租赁数据集以了解原因。

接下来，让我们详细检查随机森林超参数。

随机森林超参数

随机范围森林超参数很大，除非已经具备决策树超参数的工作知识，如第 2 章“深度决策树”中所述。

在本节中，我们将在对您已经看到的超参数进行分组之前介绍其他随机森林超参数。XGBoost 将使用其中许多超参数。

oob_score

我们的第一个超参数，也许是最有趣的，是oob_score。

随机森林通过 bagging 选择决策树，这意味着样本是通过替换选择的。在选择了所有样本之后，应该保留一些尚未选择的样本。

可以保留这些样本作为测试集。模型适合一棵树后，可以立即针对该测试集对模型进行评分。当超参数设置为oob_score=True时，这正是发生的情况。

换句话说，oob_score提供了一个获取测试分数的捷径。oob_score可以在模型拟合后立即打印出来。

让我们在人口普查数据集上使用oob_score来看看它在实践中是如何工作的。由于我们使用oob_score来测试模型，因此无需将数据拆分为训练集和测试集。

可以像往常一样使用oob_score=True初始化随机森林：

rf = RandomForestClassifier(oob_score=True, n_estimators=10, random_state=2, n_jobs=-1)

接下来，rf可能拟合数据：

rf.fit(X_census, y_census)

由于oob_score=True，在模型拟合后得分可用。可以使用模型属性.oob_score_访问它，如下所示（注意score后的下划线）：

rf.oob_score_

分数如下：

0.8343109855348423

如所述以前，oob_score是通过对在训练阶段排除的单个树上的样本进行评分来创建的。当森林中的树木数量很少时，例如有 10 个估计器的情况，可能没有足够的测试样本来最大限度地提高准确性。

更多的树意味着更多的样本，通常也意味着更高的准确性。

n_estimators

随机的当森林中有许多树木时，森林是强大的。多少才够？最近，scikit-learn 的默认值从 10 变为 100。虽然 100 棵树可能足以减少方差并获得良好的分数，但对于更大的数据集，可能需要 500 棵或更多的树。

让我们从n_estimators=50开始，看看oob_score是如何变化的：

rf = RandomForestClassifier(n_estimators=50, oob_score=True, random_state=2, n_jobs=-1)
rf.fit(X_census, y_census)
rf.oob_score_

分数如下：

0.8518780135745216

一个明确的改进。100棵树呢？

rf = RandomForestClassifier(n_estimators=100, oob_score=True, random_state=2, n_jobs=-1)
rf.fit(X_census, y_census)
rf.oob_score_

分数如下：

0.8551334418476091

这增益更小。随着n_estimators继续上升，分数最终会趋于平稳。

warm_start

warm_start超参数是非常适合确定森林中的树木数量（n_estimators）。当warm_start=True时，添加更多树不需要从头开始。如果将n_estimators从 100 更改为 200，则用 200 棵树建造森林可能需要两倍的时间。当warm_start=True时，拥有 200 棵树的随机森林不会从头开始，而是从之前模型停止的地方开始。

warm_start可用于绘制具有一系列n_estimators的各种分数。

例如，以下代码以 50 棵树为增量，从 50 开始到 500 结束，以显示一系列分数。此代码可能需要一些时间来运行，因为它通过每轮添加 50 棵新树来构建 10 个随机森林！代码按以下步骤分解：

1. 导入 matplotlib 和 seaborn，然后使用sns.set()设置 seaborn 暗网格：

   import matplotlib.pyplot as plt
   import seaborn as sns
   sns.set()

2. 初始化一个空的分数列表并使用 50 个估计器初始化一个随机森林分类器，确保warm_start=True和oob_score=True：

   oob_scores = []
   rf = RandomForestClassifier(n_estimators=50, warm_start=True, oob_score=True, n_jobs=-1, random_state=2)

3. 将rf拟合到数据集，然后将oob_score附加到oob_scores列表中：

   rf.fit(X_census, y_census)
   oob_scores.append(rf.oob_score_)

4. 准备一个估计器列表，其中包含从 50 开始的树的数量：

   est = 50
   estimators=[est]

5. 写一个 for 循环，每轮添加 50 棵树。对于每一轮，将 50 添加到est，将est附加到估计器列表中，用rf.set_params(n_estimators=est)更改n_estimators，将随机森林拟合到数据上，然后附加新的oob_score_：

   for i in range(9):
       est += 50
       estimators.append(est)
       rf.set_params(n_estimators=est)
       rf.fit(X_census, y_census)
       oob_scores.append(rf.oob_score_)

6. 为了获得漂亮的显示效果，请显示一个更大的图表，然后绘制估算器和oob_scores。添加适当的标签，然后保存并显示图表：

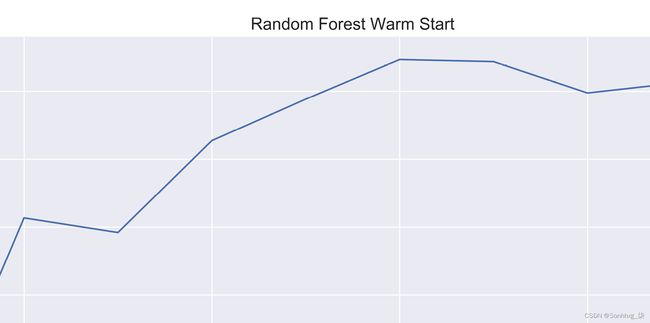
   plt.figure(figsize=(15,7))
   plt.plot(estimators, oob_scores)
   plt.xlabel('Number of Trees')
   plt.ylabel('oob_score_')
   plt.title('Random Forest Warm Start', fontsize=15)
   plt.savefig('Random_Forest_Warm_Start', dpi=325)
   plt.show()

   这个生成以下图表：

    图 3.3 – 随机森林热启动 – 每棵树的 oob_score

如您所见，树的数量趋于在 300 棵左右达到峰值。使用超过 300 棵树的成本和时间都更高，而且收益充其量是微乎其微的。

bootstrap

虽然随机森林传统上是自举的，自举超参数可以设置为False。如果bootstrap=False，则不能包含 oob_score ，因为oob_score仅在样本被遗漏时才有可能。

我们不会追求这个选项，尽管如果发生欠拟合是有道理的。

Verbose

Verbose的超参数在构建模型时，可以将其更改为更高的数字以显示更多信息。您可以自己尝试进行实验。在构建大型模型时，verbose=1可能会提供有用的信息。

决策树超参数

剩余的超参数都来自决策树。事实证明，决策树超参数在随机森林中并不重要，因为随机森林通过设计减少了方差。

以下是根据类别分组的决策树超参数供您查看。

Depth

属于这一类的超参数是：

• max_depth：总是很好调。确定发生拆分的次数。称为树的长度。减少差异的好方法。

Splits

属于这一类的超参数是：

• max_features：限制进行拆分时可供选择的功能数量。

• min_samples_split：增加新拆分所需的样本数。

• min_impurity_decrease：限制拆分以减少大于设置阈值的杂质。

Leaves

属于这一类的超参数是：

• min_samples_leaf：增加节点成为叶子所需的最小样本数。

• min_weight_fraction_leaf：成为叶子所需的总权重的分数。

有关上述超参数的更多信息，请查看官方随机森林回归器文档：https ://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html

推动随机森林边界——案例研究

想象一下，您在一家自行车租赁公司工作，您的目标是预测每个人的自行车租赁数量一天取决于天气、一天中的时间、一年中的时间和公司的发展。

在本章前面，您实现了一个带有交叉验证的随机森林回归器，以获得 945 辆自行车的 RMSE。您的目标是修改随机森林以获得可能的最低错误分数。

准备数据集

在本章前面，你下载数据集df_bikes并将其拆分为X_bikes和y_bikes。现在您正在进行一些严肃的测试，您决定将X_bikes和y_bikes 拆分为训练集和测试集，如下所示：

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_bikes, y_bikes, random_state=2)

n_estimators

首先为n_estimators选择一个合理的值。回想一下，n_estimators可以增加到以计算资源和时间为代价提高准确性。

以下是使用之前在warm_start标题下提供的相同通用代码的各种n_estimators使用warm_start方法的 RMSE 图表：

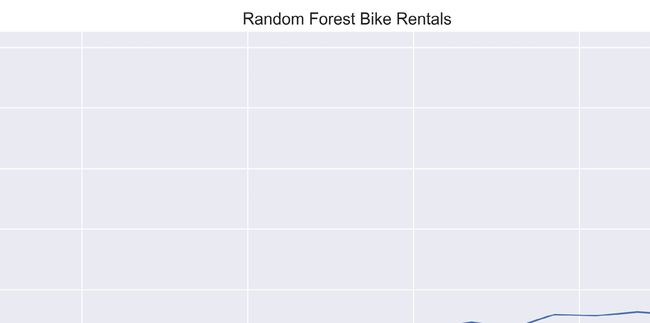
图 3.4 – 随机森林自行车租赁 – 每棵树的 RMSE

这个图表非常有趣。随机森林提供了 50 个估计器的最佳分数。在 100 个估计器之后，误差逐渐开始上升，这个概念稍后会重新讨论。

现在，使用n_estimators=50作为起点是明智的。

cross_val_score

根据上图，错误范围从 620 到 690 辆自行车租赁，是时候看看数据集的表现如何了使用cross_val_score进行交叉验证。回想一下，在交叉验证中，目的是将样本分成k个不同的折叠，并将所有样本用作不同折叠上的测试集。由于所有样本都用于测试模型，因此 oob_score将不起作用。

以下代码包含您在本章前面使用的相同步骤：

1. 初始化模型。

2. 使用带有模型、预测列、目标列、评分和折叠数作为参数的cross_val_score对模型进行评分。

3. 计算 RMSE。

4. 显示交叉验证分数和平均值。

这是代码：

rf = RandomForestRegressor(n_estimators=50, warm_start=True, n_jobs=-1, random_state=2)
scores = cross_val_score(rf, X_bikes, y_bikes, scoring='neg_mean_squared_error', cv=10)
rmse = np.sqrt(-scores)
print('RMSE:', np.round(rmse, 3))
print('RMSE mean: %0.3f' % (rmse.mean()))

输出如下：

RMSE: [ 836.482  541.898  533.086  812.782  894.877  881.117   794.103  828.968  772.517 2128.148]

RMSE mean: 902.398

这个分数比本章前面的要好。请注意，根据 RMSE 数组中的最后一个条目，最后一个折叠中的误差要高得多。这可能是由于数据或异常值中的错误。

微调超参数

是时候创建一个超参数网格来使用RandomizedSearchCV微调我们的模型了。这是一个使用RandomizedSearchCV来显示 RMSE的函数平均分数和最佳超参数：

from sklearn.model_selection import RandomizedSearchCV
def randomized_search_reg(params, runs=16, reg=RandomForestRegressor(random_state=2, n_jobs=-1)):
    rand_reg = RandomizedSearchCV(reg, params, n_iter=runs, scoring='neg_mean_squared_error', cv=10, n_jobs=-1, random_state=2)
    rand_reg.fit(X_train, y_train)
    best_model = rand_reg.best_estimator_
    best_params = rand_reg.best_params_
    print("Best params:", best_params)
    best_score = np.sqrt(-rand_reg.best_score_)
    print("Training score: {:.3f}".format(best_score))
    y_pred = best_model.predict(X_test)
    from sklearn.metrics import mean_squared_error as MSE
    rmse_test = MSE(y_test, y_pred)**0.5
    print('Test set score: {:.3f}'.format(rmse_test))

这是放置在新的random_search_reg函数中以获得第一个结果的起始超参数网格：

randomized_search_reg(params={
'min_weight_fraction_leaf':[0.0, 0.0025, 0.005, 0.0075, 0.01, 0.05],
'min_samples_split':[2, 0.01, 0.02, 0.03, 0.04, 0.06, 0.08, 0.1],
'min_samples_leaf':[1,2,4,6,8,10,20,30],
'min_impurity_decrease':[0.0, 0.01, 0.05, 0.10, 0.15, 0.2],
'max_leaf_nodes':[10, 15, 20, 25, 30, 35, 40, 45, 50, None], 
'max_features':['auto', 0.8, 0.7, 0.6, 0.5, 0.4],
'max_depth':[None,2,4,6,8,10,20]})

输出如下：

Best params: {
'min_weight_fraction_leaf': 0.0, 
'min_samples_split': 0.03, 
'min_samples_leaf': 6, 
'min_impurity_decrease': 0.05, 
'max_leaf_nodes': 25, 
'max_features': 0.7, 
'max_depth': None}

Training score: 759.076
Test set score: 701.802

这是一个重大改进。让我们看看我们是否可以通过缩小范围做得更好：

randomized_search_reg(params={
'min_samples_leaf': [1,2,4,6,8,10,20,30], 
'min_impurity_decrease':[0.0, 0.01, 0.05, 0.10, 0.15, 0.2],
'max_features':['auto', 0.8, 0.7, 0.6, 0.5, 0.4], 
'max_depth':[None,2,4,6,8,10,20]})

输出如下：

Best params: {'min_samples_leaf': 1, 
'min_impurity_decrease': 0.1, 
'max_features': 0.6, 
'max_depth': 10}

Training score: 679.052
Test set score: 626.541

分数又提高了。

现在让我们增加运行次数，并为max_depth提供更多选项：

randomized_search_reg(params={
'min_samples_leaf':[1,2,4,6,8,10,20,30],
'min_impurity_decrease':[0.0, 0.01, 0.05, 0.10, 0.15, 0.2],
'max_features':['auto', 0.8, 0.7, 0.6, 0.5, 0.4],
'max_depth':[None,4,6,8,10,12,15,20]}, runs=20)

输出如下：

Best params: {'min_samples_leaf': 1, 
'min_impurity_decrease': 0.1, 
'max_features': 0.6, 
'max_depth': 12}

Training score: 675.128
Test set score: 619.014

成绩越来越好。此时，根据之前的结果，可能值得进一步缩小范围：

randomized_search_reg(params={
'min_samples_leaf':[1,2,3,4,5,6], 
'min_impurity_decrease':[0.0, 0.01, 0.05, 0.08, 0.10, 0.12, 0.15], 
'max_features':['auto', 0.8, 0.7, 0.6, 0.5, 0.4],
'max_depth':[None,8,10,12,14,16,18,20]})

这输出如下：

Best params: {'min_samples_leaf': 1, 
'min_impurity_decrease': 0.05, 
'max_features': 0.7, 
'max_depth': 18}

Training score: 679.595
Test set score: 630.954

考试成绩又上去了。此时增加n_estimators可能是一个好主意。森林里的树越多，实现小收益的潜力就越大。

我们还可以将运行次数增加到20次，以寻找更好的超参数组合。请记住，结果基于随机搜索，而不是完整的网格搜索：

randomized_search_reg(params={
'min_samples_leaf':[1,2,4,6,8,10,20,30], 
'min_impurity_decrease':[0.0, 0.01, 0.05, 0.10, 0.15, 0.2], 
'max_features':['auto', 0.8, 0.7, 0.6, 0.5, 0.4],
'max_depth':[None,4,6,8,10,12,15,20],
'n_estimators':[100]}, runs=20)

输出如下：

Best params: {
'n_estimators': 100, 
'min_samples_leaf': 1, 
'min_impurity_decrease': 0.1, 
'max_features': 0.6, 
'max_depth': 12}

Training score: 675.128
Test set score: 619.014

这与迄今为止取得的最好成绩相匹配。我们可以继续修修补补。通过足够的实验，测试分数可能会降至 600 辆以下。但我们似乎也在 600 点附近达到顶峰。

最后，让我们将我们最好的模型放在cross_val_score中，看看结果与原始模型相比如何：

rf = RandomForestRegressor(
n_estimators=100,  
min_impurity_decrease=0.1, 
max_features=0.6, 
max_depth=12, 
warm_start=True,
 n_jobs=-1, 
random_state=2)

scores = cross_val_score(rf, X_bikes, y_bikes, scoring='neg_mean_squared_error', cv=10)
rmse = np.sqrt(-scores)
print('RMSE:', np.round(rmse, 3))
print('RMSE mean: %0.3f' % (rmse.mean()))

输出如下：

RMSE: [ 818.354  514.173  547.392  814.059  769.54   730.025  831.376  794.634  756.83  1595.237]

RMSE mean: 817.162

RMSE 回溯到817。分数比903好得多，但比619差很多。这里发生了什么？

cross_val_score的最后一次拆分可能存在问题，因为它的分数是其他分数的两倍。让我们看看改组数据是否有效。Scikit-learn 有一个 shuffle 模块，可以从sklearn.utils导入，如下所示：

from sklearn.utils import shuffle

现在我们可以按如下方式对数据进行混洗：

df_shuffle_bikes = shuffle(df_bikes, random_state=2)

现在将数据拆分为新的X和y并再次使用cross_val_score运行RandomForestRegressor：

X_shuffle_bikes = df_shuffle_bikes.iloc[:,:-1]
y_shuffle_bikes = df_shuffle_bikes.iloc[:,-1]

rf = RandomForestRegressor(n_estimators=100,  min_impurity_decrease=0.1, max_features=0.6, max_depth=12, n_jobs=-1, random_state=2)
scores = cross_val_score(rf, X_shuffle_bikes, y_shuffle_bikes, scoring='neg_mean_squared_error', cv=10)
rmse = np.sqrt(-scores)

print('RMSE:', np.round(rmse, 3))
print('RMSE mean: %0.3f' % (rmse.mean()))

输出如下：

RMSE: [630.093 686.673 468.159 526.676 593.033 724.575 774.402 672.63  760.253  616.797]
RMSE mean: 645.329

在里面shuffle数据，最后一个split没有问题，分数也高很多，和预期的一样。

随机森林的缺点

归根结底，随机森林受到其个体树木的限制。如果所有的树都犯了同样的错误，随机森林犯了这个错误。正如本案例研究在数据被洗牌之前所揭示的那样，在某些情况下，由于单个树无法解决的数据中的挑战，随机森林无法显着改善错误。

一种能够改进初始缺点的集成方法，一种可以在未来轮次中从树的错误中学习的集成方法，可能是有利的。Boosting 旨在从早期回合中树的错误中学习。提升，特别是梯度提升——下一章的重点——解决了这个主题。

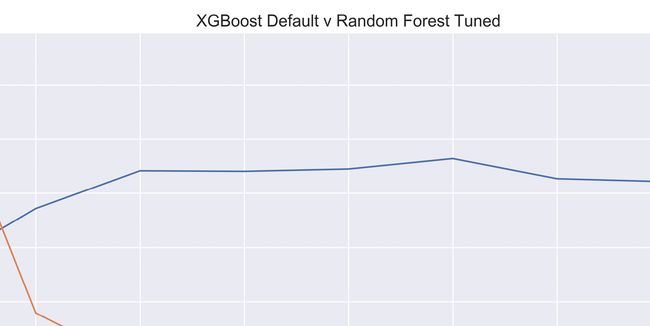
最后，下图显示了在未对数据进行混洗的情况下增加自行车租赁数据集中树的数量时调整后的随机森林回归器和默认 XGBoost 回归器的结果：

图 3.5 – 将 XGBoost 默认模型与调整后的随机森林进行比较

如您所见，XGBoost做了很多随着树木数量的增加，学习效果会更好。而且 XGBoost 模型甚至都没有调优！

概括

在本章中，您了解了集成方法的重要性。特别是，您了解了 bagging、bootstrapping 的组合、带替换的采样和聚合，将许多模型组合成一个模型。您构建了随机森林分类器和回归器。您使用 warm_start 超参数调整了 n_estimators并使用oob_score_来查找错误。然后你修改了随机森林超参数来微调模型。最后，您检查了一个案例研究，在该案例研究中，对数据进行洗牌会产生出色的结果，但与 XGBoost 相比，将更多树添加到随机森林并没有对未洗牌数据带来任何收益。

在下一章中，您将学习 boosting 的基础知识，这是一种集成方法，可以从错误中学习，以在添加更多树时提高准确性。您将实施梯度提升来进行预测，从而为极限梯度提升（更广为人知的 XGBoost）奠定基础。