深度学习梯度下降优化算法(AdaGrad、RMSProp、AdaDelta、Adam)（MXNet）

在深度学习优化算法之动量法[公式推导]（MXNet）中，动量法因为使用了指数加权移动平均，解决了自变量更新方向不一致的问题。动量法由于每个元素都使用了相同的学习率来做迭代，这也导致另外一个问题：如果x1和x2的梯度值有较大差别，那就会选择一个比较小的学习率，确保自变量在梯度值较大的维度不被发散，但是这造成了自变量在梯度值较小的维度上迭代过慢，下面的几个优化算法就是针对这个问题做的改进。

AdaGrad算法

动量法使用同一学习率带来的问题，我们采用AdaGrad算法，可以根据自变量在不同维度使用不同的学习率，避免用同样的学习率而难以适应所有维度的问题。 可以看出以前的每个元素都使用相同的学习率。现在我们把学习率在不同维度根据梯度来做调整，数学公式：

  （将小批量梯度g按元素平方累加到变量s）

 （这个学习率η就会根据上面s的变量的改变而改变）
从公式来看，各维度多出了一个的累加变量(梯度的平方的累加)，学习率相当于是除以了这个累加变量的开方的一个值，换句话说就是每个维度的学习率不同且不断变化着的。

代码： 

import d2lzh as d2l
from mxnet import nd
import math

def f_2d(x1,x2):
    return 0.1*x1**2 + 2*x2**2

def  adagrad_2d(x1,x2,s1,s2):
    g1,g2,eps=0.2*x1,4*x2,1e-6
    s1+=g1**2
    s2+=g2**2
    x1-=eta/math.sqrt(s1+eps)*g1
    x2-=eta/math.sqrt(s2+eps)*g2
    return x1,x2,s1,s2

eta=0.4
d2l.show_trace_2d(f_2d,d2l.train_2d(adagrad_2d))
#epoch 20, x1 -2.382563, x2 -0.158591

 

我们发现没有到达这个最优解的附近，原因是，这个累加的自变量作为分母，使得这个学习率是一直在下降(或不变)，也就是说迭代到了后期如果没有找到最优解，那就比较难以找到了，这个时候我们调大学习率eta=2看下：

 

 我们发现可以很快的逼近到最优解。

飞机机翼噪音测试

#https://download.csdn.net/download/weixin_41896770/86513479
import d2lzh as d2l
from mxnet import nd
import math

features,labels=d2l.get_data_ch7()

def init_adagrad_states():
    s_w=nd.zeros((features.shape[1],1))
    s_b=nd.zeros(1)
    return s_w,s_b

def adagrad(params,states,hyperparams):
    eps=1e-6
    for p,s in zip(params,states):
        s[:]+=p.grad.square()
        p[:]-=hyperparams['lr']/(s+eps).sqrt() * p.grad

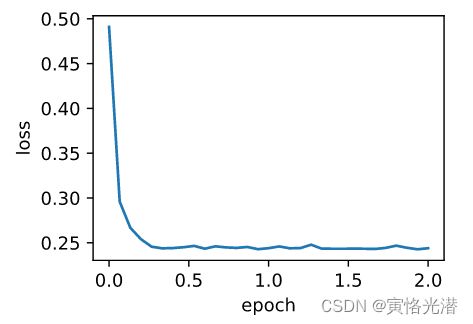
d2l.train_ch7(adagrad,init_adagrad_states(),{'lr':0.1},features,labels)
#loss: 0.243906, 0.197325 sec per epoch

#简洁实现
d2l.train_gluon_ch7('adagrad',{'learning_rate':0.1},features,labels)

RMSProp算法

上面的AdaGrad存在自变量每个元素的学习率在迭代过程中会一直降低(或不变)，如果没有及时找到最优解，后面就比较难以找到的问题，RMSProp做了一点修改，使用了指数加权移动平均的做法。

数学公式：

s这个累加自变量，是对梯度的平方做指数加权移动平均，这样一来，自变量的每个元素的学习率在迭代过程中就不再一直降低(或不变)

代码： 

import d2lzh as d2l
from mxnet import nd
import math

def f_2d(x1,x2):
    return 0.1*x1**2 +2*x2**2

def rmsprop_2d(x1,x2,s1,s2):
    g1,g2,eps=0.2*x1,4*x2,1e-6
    s1=gamma*s1 + (1-gamma)*g1**2
    s2=gamma*s2 + (1-gamma)*g2**2
    x1-=eta/math.sqrt(s1+eps)*g1
    x2-=eta/math.sqrt(s2+eps)*g2
    return x1,x2,s1,s2

eta,gamma=0.4,0.9
d2l.show_trace_2d(f_2d,d2l.train_2d(rmsprop_2d))
#epoch 20, x1 -0.010599, x2 0.000000

 

 

图中可以看出这个算法能够快速的逼近最优解，解决了AdaGrad学习率不断减小，使得后期找不到最优解的问题。

飞机机翼噪音测试

import d2lzh as d2l
from mxnet import nd
import math

#如果想知道某个函数的源码，比如：print(d2l.get_data_ch7.__code__)
#将显示这个函数所在文件的目录地址，打开查看即可
features,labels=d2l.get_data_ch7()

def init_rmsprop_states():
    s_w=nd.zeros((features.shape[1],1))
    s_b=nd.zeros(1)
    return (s_w,s_b)
    
def rmsprop(params,states,hyperparams):
    gamma,eps=hyperparams['gamma'],1e-6
    for p,s in zip(params,states):
        s[:]=gamma*s + (1-gamma)*p.grad.square()
        p[:]-=hyperparams['lr']/(s+eps).sqrt() * p.grad

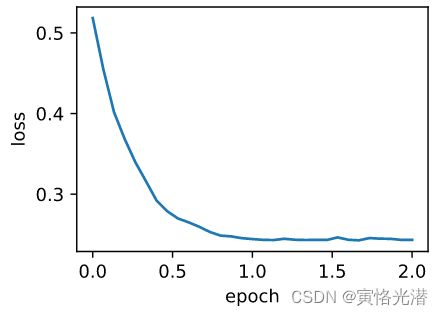
d2l.train_ch7(rmsprop,init_rmsprop_states(),{'lr':0.01,'gamma':0.9},features,labels)
#loss: 0.242604, 0.246025 sec per epoch

#简洁实现
d2l.train_gluon_ch7('rmsprop',{'learning_rate':0.01,'gamma1':0.9},features,labels)

AdaDelta算法

AdaDelta算法也是针对AdaGrad算法在迭代后期很难找最优解的问题做的改进，我们来看下数学公式：

 （这个s自变量跟RMSProp算法一样）

可以看到跟RMSProp算法比较，没有了η学习率，多出一个的状态变量，其中这个是对自变量的平方做指数加权移动平均，可以将看做是η学习率。 

代码：

import d2lzh as d2l
from mxnet import nd
import math

#如果想知道某个函数的源码，比如：print(d2l.get_data_ch7.__code__)
#将显示这个函数所在文件的目录地址，打开查看即可
features,labels=d2l.get_data_ch7()

def init_adadelta_states():
    s_w,s_b=nd.zeros((features.shape[1],1)),nd.zeros(1)
    delta_w,delta_b=nd.zeros((features.shape[1],1)),nd.zeros(1)
    return ((s_w,delta_w),(s_b,delta_b))

def adadelta(params,states,hyperparams):
    rho,eps=hyperparams['rho'],1e-5
    for p,(s,delta) in zip(params,states):
        s[:]=rho*s + (1-rho)*p.grad.square()
        g=(((delta+eps)/(s+eps)).sqrt()) * p.grad
        p[:]-=g
        delta[:]=rho*delta + (1-rho)*(g**2)

rho=0.9

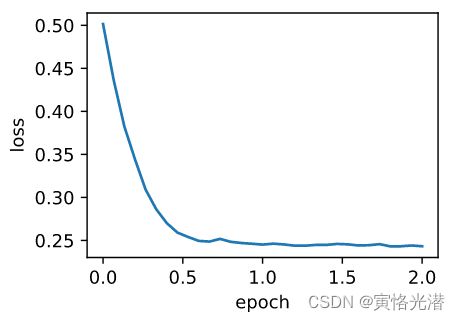
d2l.train_ch7(adadelta,init_adadelta_states(),{'rho':0.9},features,labels)
#loss: 0.243291, 0.279038 sec per epoch

#简洁实现
d2l.train_gluon_ch7('adadelta',{'rho':0.9},features,labels)

Adam算法(动量法+RMSProp)

Adam是一个用途很广泛很有用处的优化算法，有兴趣的可以看原论文：ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION
论文中说明这个算法是结合了AdaGrad和RMSProp的优点，AdaGrad在稀疏梯度上表现很好，RMSProp在在线(on-line)和非平稳(non-stationary)目标函数上表现很好，上述的这两种算法也是很流行的。
另外也可以看作是在RMSProp算法基础上对小批量随机梯度也做了指数加权移动平均，结合了动量法的一种变体。
Adam算法有如下一些优点：

1、占用内存小
2、参数更新的幅度不会随着梯度的重缩放(rescaling)改变
3、对目标函数要求不高，可以是非稳定的
4、同AdaGrad一样可以处理稀疏梯度(sparse gradient)
5、可以自然地执行步长退火的形式(a form of step size annealing)，了解退火算法的伙伴们知道这可能可以得到全局最优解而不仅是局部最优解。
6、能很好的适配非凸优化问题(non convex optimization)

数学公式：

 

  （偏差修正）

当t较小时，过去各时间步小批量随机梯度权值之和会较小，例如，当=0.9时，=0.1，为了消除这样的影响，对于任意时间步t，我们可以将再除以，从而使过去各时间步小批量随机梯度权值之和为1，这种操作叫做偏差修正。

代码：

import d2lzh as d2l
from mxnet import nd
import math

#如果想知道某个函数的源码，比如：print(d2l.get_data_ch7.__code__)
#将显示这个函数所在文件的目录地址，打开查看即可
features,labels=d2l.get_data_ch7()

def init_adam_states():
    v_w,v_b=nd.zeros((features.shape[1],1)),nd.zeros(1)
    s_w,s_b=nd.zeros((features.shape[1],1)),nd.zeros(1)
    return ((v_w,s_w),(v_b,s_b))

def adam(params,states,hyperparams):
    beta1,beta2,eps=0.9,0.999,1e-6
    for p,(v,s) in zip(params,states):
        v[:]=beta1*v + (1-beta1)*p.grad
        s[:]=beta2*s + (1-beta2)*p.grad.square()
        v_bias_corr=v/(1 - beta1**hyperparams['t'])
        s_bias_corr=s/(1 - beta2**hyperparams['t'])
        p[:]-=hyperparams['lr']*v_bias_corr / (s_bias_corr.sqrt()+eps)
    hyperparams['t']+=1

d2l.train_ch7(adam,init_adam_states(),{'lr':0.01,'t':1},features,labels)
#loss: 0.243235, 0.283553 sec per epoch

#简洁实现
d2l.train_gluon_ch7('adam',{'learning_rate':0.01},features,labels)