NNDL 实验五 前馈神经网络（1）二分类任务

4.1 神经元

4.1.1 净活性值

假设一个神经元接收的输入为x∈RD，其权重向量为w∈RD，神经元所获得的输入信号，即净活性值z的计算方法为z=wTx+b，其中b为偏置。
为了提高预测样本的效率，我们通常会将N个样本归为一组进行成批地预测。
z=Xw+b,(4.2),其中X∈RN×D为N个样本的特征矩阵，z∈RN为N个预测值组成的列向量。
1.使用pytorch计算一组输入的净活性值，代码参考paddle例题：

import torch

# 2个特征数为5的样本
X = torch.rand([2, 5])

# 含有5个参数的权重向量
w = torch.rand([5, 1])
# 偏置项
b = torch.rand([1, 1])

# 使用'torch.matmul'实现矩阵相乘
z = torch.matmul(X, w) + b
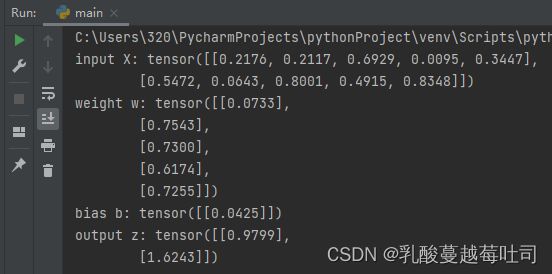
print("input X:", X)
print("weight w:", w, "\nbias b:", b)
print("output z:", z)

2.在pytorch中学习相应函数torch.nn.Linear(features_in, features_out, bias=False)。
实现上面的例子，完成代码。

import torch
import torch.nn as nn
from torch.autograd import Variable

m = nn.Linear(5, 1)
input = Variable(torch.rand(2, 5)) #包装Tensor使得支持自动微分
output = m(input)
print(output)

3.进一步深入研究torch.nn.Linear()的使用。
PyTorch的nn.Linear（）是用于设置网络中的全连接层的，需要注意在二维图像处理的任务中，全连接层的输入与输出一般都设置为二维张量，形状通常为[batch_size, size]，不同于卷积层要求输入输出是四维张量。其用法与形参说明如下：
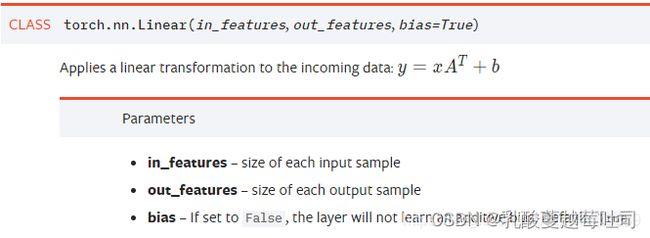in_features指的是输入的二维张量的大小，即输入的[batch_size, size]中的size。
out_features指的是输出的二维张量的大小，即输出的二维张量的形状为[batch_size，output_size]，当然，它也代表了该全连接层的神经元个数。
从输入输出的张量的shape角度来理解，相当于一个输入为[batch_size, in_features]的张量变换成了[batch_size, out_features]的输出张量。
参考文章：PyTorch的nn.Linear（）详解

【思考题】加权相加与仿射变换之间有什么区别和联系？
对于矩阵乘上一个权重加上另一个偏置b就是我理解狭义上的加权相加；仿射变换是指通过一个线性变换和一个平移，将一个向量空间变换成另一个向量空间的过程。

区别：由上两句话能看出加权相加后的结果向量空间的原点不变，也就是绝对位置不变；而仿射变换因为进行了平移操作，它的原点是发生变化的，也就是变换成了另一个向量空间。

联系：首先二者相同点是变换前后整体形状保持不变，比如变换前为直线，变换后仍然是直线。其次，二者变换后直线比例保持不变。其实两者进行的操作大同小异。

对于加权相加一个直观图：

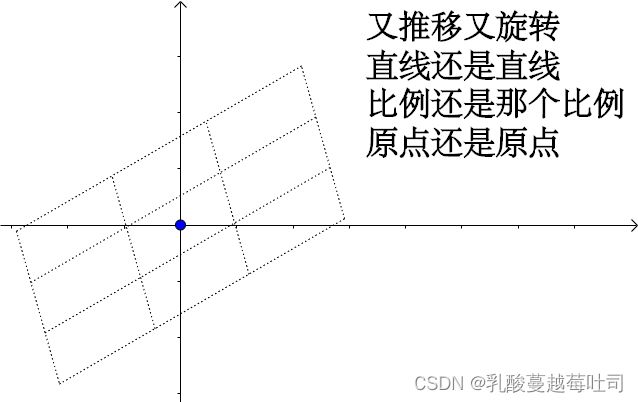
对于仿射变换一个直观图：

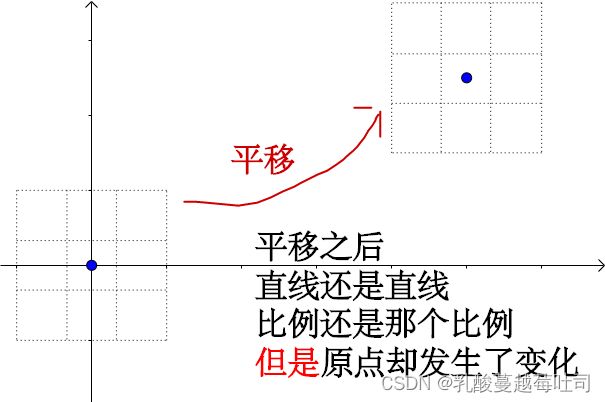
结合之前的描述，维基百科“仿射变换”词条里的一个gif动图，非常生动的表明了这一过程：
仿射变换gif动图

4.1.2 激活函数

净活性值z再经过一个非线性函数f(⋅)后，得到神经元的活性值a。
a=f(z),激活函数通常为非线性函数，可以增强神经网络的表示能力和学习能力。常用的激活函数有S型函数和ReLU函数。

4.1.2.1 Sigmoid 型函数

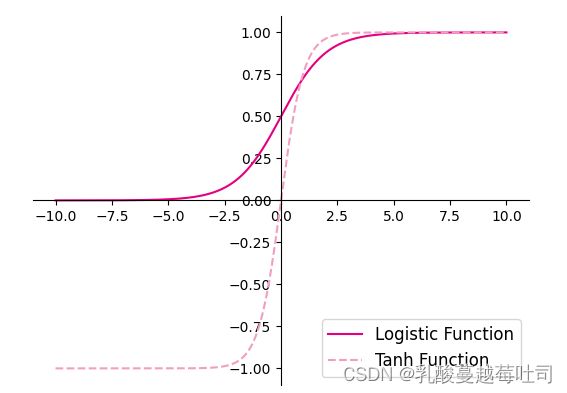
Sigmoid 型函数是指一类S型曲线函数，为两端饱和函数。常用的 Sigmoid 型函数有 Logistic 函数和 Tanh 函数，其数学表达式为Logistic 函数：σ(z)=11+exp(−z)；
tanh 函数：tanh(z)=exp(z−exp(−z)exp(z)+exp(−z)。
1.Logistic函数和Tanh函数的代码实现和可视化如下：

import matplotlib.pyplot as plt

# Logistic函数
def logistic(z):
    return 1.0 / (1.0 + torch.exp(-z))

# Tanh函数
def tanh(z):
    return (torch.exp(z) - torch.exp(-z)) / (torch.exp(z) + torch.exp(-z))

# 在[-10,10]的范围内生成10000个输入值，用于绘制函数曲线
z = torch.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z.tolist(), logistic(z).tolist(), color='#e4007f', label="Logistic Function")
plt.plot(z.tolist(), tanh(z).tolist(), color='#f19ec2', linestyle ='--', label="Tanh Function")

ax = plt.gca() # 获取轴，默认有4个
# 隐藏两个轴，通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 调整坐标轴位置
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')

plt.savefig('fw-logistic-tanh.pdf')
plt.show()

2.在pytorch中找到相应函数并测试。

import torch
import matplotlib.pyplot as plt

# 在[-10,10]的范围内生成10000个输入值，用于绘制函数曲线
z = torch.linspace(-10, 10, 10000)

plt.figure()
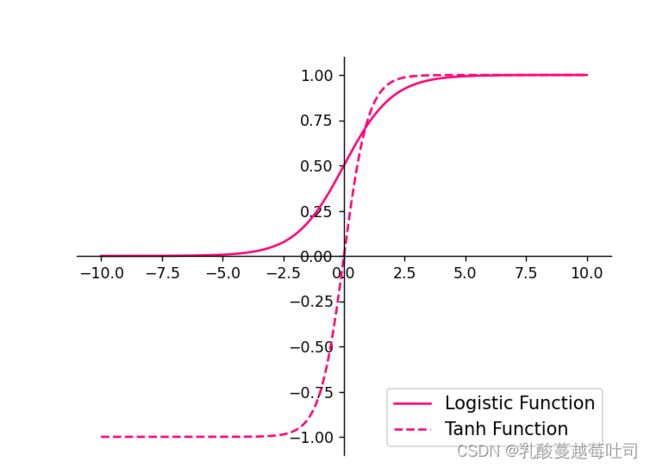
plt.plot(z.tolist(), torch.sigmoid(z).tolist(), color='#ff0077', label="Logistic Function")
plt.plot(z.tolist(), torch.tanh(z).tolist(), color='#ff0077', linestyle ='--', label="Tanh Function")

ax = plt.gca() # 获取轴，默认有4个
# 隐藏两个轴，通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 调整坐标轴位置   
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')
plt.show()

4.1.2.2 ReLU型函数

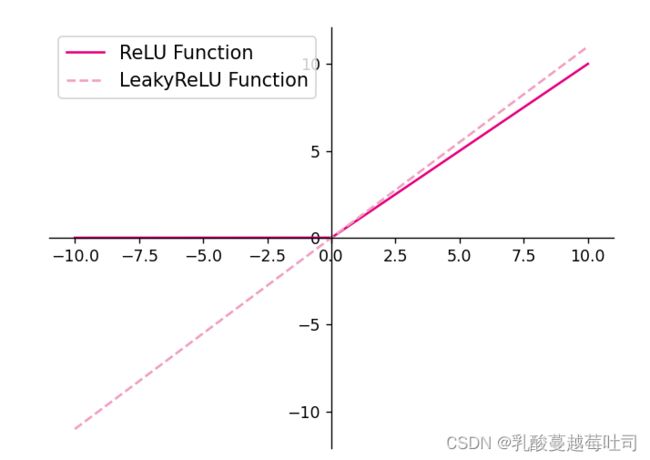
常见的ReLU函数有ReLU和带泄露的ReLU（Leaky ReLU），数学表达式分别为：ReLU(z)=max(0,z)；
LeakyReLU(z)=max(0,z)+λmin(0,z)，其中λ为超参数。
1.使用python实现并可视化可视化“ReLU、带泄露的ReLU的函数”。

# ReLU
def relu(z):
    return torch.maximum(z, torch.tensor(0.))

# 带泄露的ReLU
def leaky_relu(z, negative_slope=0.1):
    # 当前版本paddle暂不支持直接将bool类型转成int类型，因此调用了paddle的cast函数来进行显式转换
    a1 = (z * z)
    a2 = (z * (negative_slope * z))
    return a1 + a2

# 在[-10,10]的范围内生成一系列的输入值，用于绘制relu、leaky_relu的函数曲线
z = torch.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z.tolist(), relu(z).tolist(), color="#e4007f", label="ReLU Function")
plt.plot(z.tolist(), leaky_relu(z).tolist(), color="#f19ec2", linestyle="--", label="LeakyReLU Function")

ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='upper left', fontsize='large')
plt.savefig('fw-relu-leakyrelu.pdf')
plt.show()

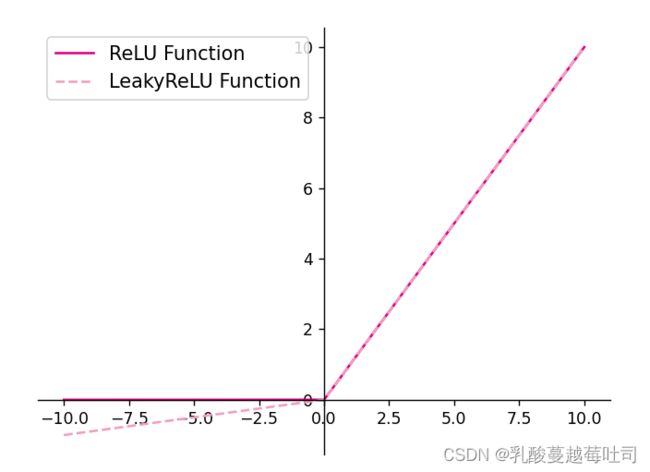
2.在pytorch中找到相应函数并测试。

import torch
import matplotlib.pyplot as plt


# 在[-10,10]的范围内生成一系列的输入值，用于绘制relu、leaky_relu的函数曲线
z = torch.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z.tolist(), torch.relu(z).tolist(), color="#e4007f", label="ReLU Function")
plt.plot(z.tolist(), torch.nn.LeakyReLU(0.1)(z), color="#f19ec2", linestyle="--", label="LeakyReLU Function")

ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='upper left', fontsize='large')
plt.savefig('fw-relu-leakyrelu.pdf')
plt.show()

4.2 基于前馈神经网络的二分类任务

4.2.1 数据集构建

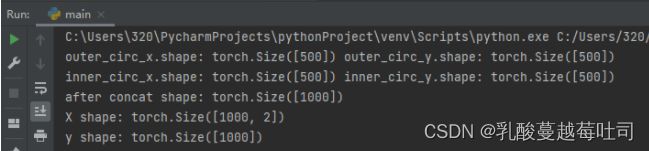
这里，我们使用第3.1.1节中构建的二分类数据集：Moon1000数据集，其中训练集640条、验证集160条、测试集200条。
该数据集的数据是从两个带噪音的弯月形状数据分布中采样得到，每个样本包含2个特征。

# 采样1000个样本
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.5)

num_train = 640
num_dev = 160
num_test = 200

X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]

y_train = y_train.reshape([-1,1])
y_dev = y_dev.reshape([-1,1])
y_test = y_test.reshape([-1,1])

4.2.2 模型构建

为了更高效的构建前馈神经网络，我们先定义每一层的算子，然后再通过算子组合构建整个前馈神经网络。
假设网络的第l层的输入为第l−1层的神经元活性值a(l−1)，经过一个仿射变换，得到该层神经元的净活性值z，再输入到激活函数得到该层神经元的活性值a。
在实践中，为了提高模型的处理效率，通常将N个样本归为一组进行成批地计算。假设网络第l层的输入为A(l−1)∈RN×Ml−1，其中每一行为一个样本，则前馈网络中第l层的计算公式为
Z(l)=A(l−1)W(l)+b(l)∈RN×Ml,(4.8)
A(l)=fl(Z(l))∈RN×Ml,(4.9)
其中Z(l)为N个样本第l层神经元的净活性值，A(l)为N个样本第l层神经元的活性值，W(l)∈RMl−1×Ml为第l层的权重矩阵，b(l)∈R1×Ml为第l层的偏置。
为了和代码的实现保存一致性，这里使用形状为(样本数量×特征维度)的张量来表示一组样本。样本的矩阵X是由N个x的行向量组成。而《神经网络与深度学习》中x为列向量，因此这里的权重矩阵W和偏置b和《神经网络与深度学习》中的表示刚好为转置关系。
为了使后续的模型搭建更加便捷，我们将神经层的计算，即公式(4.8)和(4.9)，都封装成算子，这些算子都继承Op基类。

4.2.2.1 线性层算子

公式（4.8）对应一个线性层算子，权重参数采用默认的随机初始化，偏置采用默认的零初始化。代码实现如下：

# 实现线性层算子
class Linear(Op):
    def __init__(self, input_size, output_size, name, weight_init=torch.normal, bias_init=torch.zeros):
        """
        输入：
            - input_size：输入数据维度
            - output_size：输出数据维度
            - name：算子名称
            - weight_init：权重初始化方式，默认使用'paddle.standard_normal'进行标准正态分布初始化
            - bias_init：偏置初始化方式，默认使用全0初始化
        """

        self.params = {}
        # 初始化权重
        self.params['W'] = weight_init([input_size, output_size])
        # 初始化偏置
        self.params['b'] = bias_init([1, output_size])
        self.inputs = None

        self.name = name

    def forward(self, inputs):
        """
        输入：
            - inputs：shape=[N,input_size], N是样本数量
        输出：
            - outputs：预测值，shape=[N,output_size]
        """
        self.inputs = inputs

        outputs = torch.matmul(self.inputs, self.params['W']) + self.params['b']
        return outputs

4.2.2.2 Logistic算子

本节我们采用Logistic函数来作为公式(4.9)中的激活函数。这里也将Logistic函数实现一个算子，代码实现如下：

class Logistic(Op):
    def __init__(self):
        self.inputs = None
        self.outputs = None

    def forward(self, inputs):
        """
        输入：
            - inputs: shape=[N,D]
        输出：
            - outputs：shape=[N,D]
        """
        outputs = 1.0 / (1.0 + torch.exp(-inputs))
        self.outputs = outputs
        return outputs

4.2.2.3 层的串行组合

在定义了神经层的线性层算子和激活函数算子之后，我们可以不断交叉重复使用它们来构建一个多层的神经网络。
下面我们实现一个两层的用于二分类任务的前馈神经网络，选用Logistic作为激活函数，可以利用上面实现的线性层和激活函数算子来组装。代码实现如下：

# 实现一个两层前馈神经网络
class Model_MLP_L2(Op):
    def __init__(self, input_size, hidden_size, output_size):
        """
        输入：
            - input_size：输入维度
            - hidden_size：隐藏层神经元数量
            - output_size：输出维度
        """
        self.fc1 = Linear(input_size, hidden_size, name="fc1")
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()

    def __call__(self, X):
        return self.forward(X)

    def forward(self, X):
        """
        输入：
            - X：shape=[N,input_size], N是样本数量
        输出：
            - a2：预测值，shape=[N,output_size]
        """
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        return a2

测试一下
现在，我们实例化一个两层的前馈网络，令其输入层维度为5，隐藏层维度为10，输出层维度为1。
并随机生成一条长度为5的数据输入两层神经网络，观察输出结果。

# 实例化模型
model = Model_MLP_L2(input_size=5, hidden_size=10, output_size=1)
# 随机生成1条长度为5的数据
X = torch.rand([1, 5])
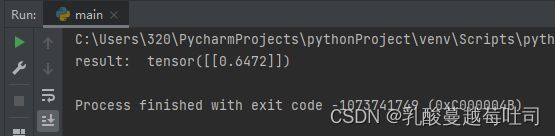
result = model(X)
print ("result: ", result)

报错解决点：
paddle.normal对应np.random.standard_normal

在初始化权重后转换为tensor：self.params[‘W’] = torch.as_tensor(self.params[‘W’], dtype=torch.float32)

4.2.3 损失函数

二分类交叉熵损失函数见第三章，这里不再赘述。

4.2.4 模型优化

神经网络的参数主要是通过梯度下降法进行优化的，因此需要计算最终损失对每个参数的梯度。
由于神经网络的层数通常比较深，其梯度计算和上一章中的线性分类模型的不同的点在于：线性模型通常比较简单可以直接计算梯度，而神经网络相当于一个复合函数，需要利用链式法则进行反向传播来计算梯度。

4.2.4.1 反向传播算法

前馈神经网络的参数梯度通常使用误差反向传播算法来计算。使用误差反向传播算法的前馈神经网络训练过程可以分为以下三步：

• 前馈计算每一层的净活性值Z(l)和激活值A(l)，直到最后一层；
• 反向传播计算每一层的误差项δ(l)=∂R∂Z(l)；
• 计算每一层参数的梯度，并更新参数。
  在上面实现算子的基础上，来实现误差反向传播算法。在上面的三个步骤中，
  第1步是前向计算，可以利用算子的forward()方法来实现；
  第2步是反向计算梯度，可以利用算子的backward()方法来实现；
  第3步中的计算参数梯度也放到backward()中实现，更新参数放到另外的优化器中专门进行。
  这样，在模型训练过程中，我们首先执行模型的forward()，再执行模型的backward()，就得到了所有参数的梯度，之后再利用优化器迭代更新参数。
  以这我们这节中构建的两层全连接前馈神经网络Model_MLP_L2为例，下图给出了其前向和反向计算过程：
  
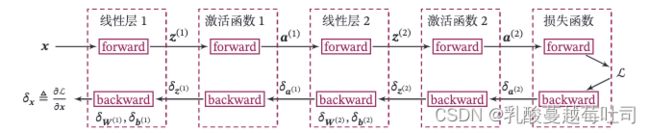
  下面我们按照反向的梯度传播顺序，为每个算子添加backward()方法，并在其中实现每一层参数的梯度的计算。

4.2.4.2 损失函数

二分类交叉熵损失函数对神经网络的输出y^的偏导数为:

其中dialog(x)表示以向量x为对角元素的对角阵，1x=1x1,…,1xN表示逐元素除，⊙表示逐元素积。
实现损失函数的backward()，代码实现如下：

# 实现交叉熵损失函数
class BinaryCrossEntropyLoss(Op):
    def __init__(self, model):
        self.predicts = None
        self.labels = None
        self.num = None

        self.model = model

    def __call__(self, predicts, labels):
        return self.forward(predicts, labels)

    def forward(self, predicts, labels):
        """
        输入：
            - predicts：预测值，shape=[N, 1]，N为样本数量
            - labels：真实标签，shape=[N, 1]
        输出：
            - 损失值：shape=[1]
        """
        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss = -1. / self.num * (torch.matmul(self.labels.t(), torch.log(self.predicts))
                                 + torch.matmul((1 - self.labels.t()), torch.log(1 - self.predicts)))

        loss = torch.squeeze(loss, axis=1)
        return loss

    def backward(self):
        # 计算损失函数对模型预测的导数
        loss_grad_predicts = -1.0 * (self.labels / self.predicts -
                                     (1 - self.labels) / (1 - self.predicts)) / self.num

        # 梯度反向传播
        self.model.backward(loss_grad_predicts)

4.2.4.3 Logistic算子

在本节中，我们使用Logistic激活函数，所以这里为Logistic算子增加的反向函数。
Logistic算子的前向过程表示为A=σ(Z)，其中σ为Logistic函数，Z∈RN×D和A∈RN×D的每一行表示一个样本。
为了简便起见，我们分别用向量a∈RD 和 z∈RD表示同一个样本在激活函数前后的表示，则a对z的偏导数为：

按照反向传播算法，令δa=∂R∂a∈RD表示最终损失R对Logistic算子的单个输出a的梯度，则

将上面公式利用批量数据表示的方式重写，令δA=∂R∂A∈RN×D表示最终损失R对Logistic算子输出A的梯度，损失函数对Logistic函数输入Z的导数为

δZ为Logistic算子反向传播的输出。
由于Logistic函数中没有参数，这里不需要在backward()方法中计算该算子参数的梯度。

class Logistic(Op):
    def __init__(self):
        self.inputs = None
        self.outputs = None
        self.params = None

    def forward(self, inputs):
        outputs = 1.0 / (1.0 + torch.exp(-inputs))
        self.outputs = outputs
        return outputs

    def backward(self, grads):
        # 计算Logistic激活函数对输入的导数
        outputs_grad_inputs = torch.multiply(self.outputs, (1.0 - self.outputs))
        return torch.multiply(grads,outputs_grad_inputs)

4.2.4.4 线性层

线性层算子Linear的前向过程表示为Y=XW+b，其中输入为X∈RN×M，输出为Y∈RN×D，参数为权重矩阵W∈RM×D和偏置b∈R1×D。X和Y中的每一行表示一个样本。
为了简便起见，我们用向量x∈RM和y∈RD表示同一个样本在线性层算子中的输入和输出，则有y=WTx+bT。y对输入x的偏导数为

线性层输入的梯度 按照反向传播算法，令δy=∂R∂y∈RD表示最终损失R对线性层算子的单个输出y的梯度，则
δx≜∂R∂x=Wδy。(4.18)
将上面公式利用批量数据表示的方式重写，令δY=∂R∂Y∈RN×D表示最终损失R对线性层算子输出Y的梯度，公式可以重写为
δX=δYWT,(4.19)
其中δX为线性层算子反向函数的输出。
计算线性层参数的梯度 由于线性层算子中包含有可学习的参数W和b，因此backward()除了实现梯度反传外，还需要计算算子内部的参数的梯度。
令δy=∂R∂y∈RD表示最终损失R对线性层算子的单个输出y的梯度，则
δW≜∂R∂W=xδTy,(4.20)δb≜∂R∂b=δTy。(4.21)
将上面公式利用批量数据表示的方式重写，令δY=∂R∂Y∈RN×D表示最终损失R对线性层算子输出Y的梯度，则公式可以重写为
δW=XTδY,(4.22)δb=1TδY。(4.23)
具体实现代码如下：

class Linear(Op):
    def __init__(self, input_size, output_size, name, weight_init=torch.normal, bias_init=torch.zeros):
        self.params = {}
        self.params['W'] = weight_init(mean=0.,std=1.,size=[input_size,output_size])
        self.params['b'] = bias_init([1, output_size])

        self.inputs = None
        self.grads = {}

        self.name = name

    def forward(self, inputs):
        self.inputs = inputs
        outputs = torch.matmul(self.inputs, self.params['W']) + self.params['b']
        return outputs

    def backward(self, grads):
        """
        输入：
            - grads：损失函数对当前层输出的导数
        输出：
            - 损失函数对当前层输入的导数
        """
        self.grads['W'] = torch.matmul(self.inputs.T, grads)
        self.grads['b'] = torch.sum(grads, axis=0)

        # 线性层输入的梯度
        return torch.matmul(grads, self.params['W'].T)

4.2.4.5 整个网络

实现完整的两层神经网络的前向和反向计算。代码实现如下：

class Model_MLP_L2(Op):
    def __init__(self, input_size, hidden_size, output_size):
        # 线性层
        self.fc1 = Linear(input_size, hidden_size, name="fc1")
        # Logistic激活函数层
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()

        self.layers = [self.fc1, self.act_fn1, self.fc2, self.act_fn2]

    def __call__(self, X):
        return self.forward(X)

    # 前向计算
    def forward(self, X):
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        return a2
        
    # 反向计算
    def backward(self, loss_grad_a2):
        loss_grad_z2 = self.act_fn2.backward(loss_grad_a2)
        loss_grad_a1 = self.fc2.backward(loss_grad_z2)
        loss_grad_z1 = self.act_fn1.backward(loss_grad_a1)
        loss_grad_inputs = self.fc1.backward(loss_grad_z1)

4.2.4.6 优化器

在计算好神经网络参数的梯度之后，我们将梯度下降法中参数的更新过程实现在优化器中。

与第3章中实现的梯度下降优化器SimpleBatchGD不同的是，此处的优化器需要遍历每层，对每层的参数分别做更新。

class BatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(BatchGD, self).__init__(init_lr=init_lr, model=model)

    def step(self):
        # 参数更新
        for layer in self.model.layers: # 遍历所有层
            if isinstance(layer.params, dict):
                for key in layer.params.keys():
                    layer.params[key] = layer.params[key] - self.init_lr * layer.grads[key]

4.2.5 完善Runner类：RunnerV2_1

1.支持自定义算子的梯度计算，在训练过程中调用self.loss_fn.backward()从损失函数开始反向计算梯度；
2.每层的模型保存和加载，将每一层的参数分别进行保存和加载。

class RunnerV2_1(object):
    def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric

        # 记录训练过程中的评估指标变化情况
        self.train_scores = []
        self.dev_scores = []

        # 记录训练过程中的评价指标变化情况
        self.train_loss = []
        self.dev_loss = []

    def train(self, train_set, dev_set, **kwargs):
        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs", 100)

        # 传入模型保存路径
        save_dir = kwargs.get("save_dir", None)

        # 记录全局最优指标
        best_score = 0
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            X, y = train_set
            # 获取模型预测
            logits = self.model(X)
            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y)  # return a tensor

            self.train_loss.append(trn_loss.item())
            # 计算评估指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)

            self.loss_fn.backward()

            # 参数更新
            self.optimizer.step()

            dev_score, dev_loss = self.evaluate(dev_set)
            # 如果当前指标为最优指标，保存该模型
            if dev_score > best_score:
                print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score
                if save_dir:
                    self.save_model(save_dir)

            if log_epochs and epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")

    def evaluate(self, data_set):
        X, y = data_set
        # 计算模型输出
        logits = self.model(X)
        # 计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)
        # 计算评估指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)
        return score, loss

    def predict(self, X):
        return self.model(X)

    def save_model(self, save_dir):
        # 对模型每层参数分别进行保存，保存文件名称与该层名称相同
        for layer in self.model.layers:  # 遍历所有层
            if isinstance(layer.params, dict):
               torch.save(layer.params, os.path.join(save_dir, layer.name+".pdparams"))

    def load_model(self, model_dir):
        # 获取所有层参数名称和保存路径之间的对应关系
        model_file_names = os.listdir(model_dir)
        name_file_dict = {}
        for file_name in model_file_names:
            name = file_name.replace(".pdparams", "")
            name_file_dict[name] = os.path.join(model_dir, file_name)

        # 加载每层参数
        for layer in self.model.layers:  # 遍历所有层
            if isinstance(layer.params, dict):
                name = layer.name
                file_path = name_file_dict[name]
                layer.params = torch.load(file_path)

4.2.6 模型训练

使用训练集和验证集进行模型训练，共训练2000个epoch。评价指标为accuracy。

epoch_num = 1000

model_saved_dir = 'D:\\apps\python\pytorch\save'

# 输入层维度为2
input_size = 2
# 隐藏层维度为5
hidden_size = 5
# 输出层维度为1
output_size = 1

# 定义网络
model = Model_MLP_L2(input_size=input_size, hidden_size=hidden_size, output_size=output_size)

# 损失函数
loss_fn = BinaryCrossEntropyLoss(model)

# 优化器
learning_rate = 0.2
optimizer = BatchGD(learning_rate, model)

# 评价方法
metric = accuracy

# 实例化RunnerV2_1类，并传入训练配置
runner = RunnerV2_1(model, optimizer, metric, loss_fn)

runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_dir=model_saved_dir)

这里model_saved_dir不知道后面写什么，看的同学博客才知道是写文件夹的路径。

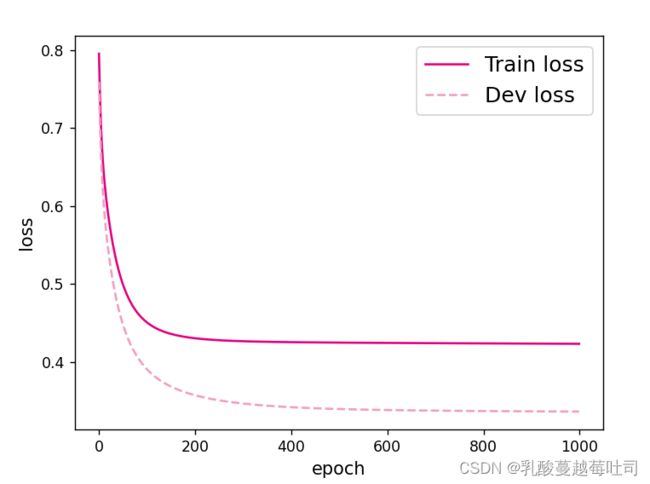
可视化观察训练集与验证集的损失函数变化情况。

import matplotlib.pyplot as plt
# 打印训练集和验证集的损失
plt.figure()
plt.plot(range(epoch_num), runner.train_loss, color="#e4007f", label="Train loss")
plt.plot(range(epoch_num), runner.dev_loss, color="#f19ec2", linestyle='--', label="Dev loss")
plt.xlabel("epoch", fontsize='large')
plt.ylabel("loss", fontsize='large')
plt.legend(fontsize='x-large')
plt.show()
#加载训练好的模型
runner.load_model(model_saved_dir)
# 在测试集上对模型进行评价
score, loss = runner.evaluate([X_test, y_test])

4.2.7 性能评价

使用测试集对训练中的最优模型进行评价，观察模型的评价指标。代码实现如下：

# 加载训练好的模型
runner.load_model(model_saved_dir)
# 在测试集上对模型进行评价
score, loss = runner.evaluate([X_test, y_test])

print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

从结果来看，模型在测试集上取得了较高的准确率。
在这更深了解了一下学习率、过拟合：
学习率：学习率lr表征了参数每次更新的幅度，设置过大，参数不容易收敛。因为绝大多数的机器学习问题，不是一个凸优化的问题，很多时候找的解不是全局最优解而是局部最优解。我们需要找loss函数的极小值，（二维图上看来就是找那些’坑’)。所以loss函数的下降过程，是比较wiggly的，曲曲折折的。如果这个时候学习率设置得过大，就可能导致直接从一个坑跳到另一个坑，甚至可能几个坑来回跳，就收敛不了，或者收敛很慢了；设置过小，参数更新会很慢（时间会很长）。还是上面的例子，如果初始点选的不好，比如选在了一个山头，学习率设置的过小，比如一次一小步，那么训练到走到坑里就要走很长时间。就是参数的更新很慢，需要很多的训练（步数），才能找到合适的参数。
所以在实际的应用中，学习率的选择，一般是先大后小。先大可以让loss函数尽快的往loss小的方向下降，等到了坑里，学习率就要慢慢的减小，防止直接跳出坑。所以最好的方式，就是先比较大，然后慢慢缩减变小。
过拟合：选好了参数之后，进行训练，发现随着迭代次数的升高，模型的loss出现了先降低，后升高的问题，这个就是模型过拟合了。意思就是太过于学习了训练集的分布，从而使得模型的泛化能力变差了。或者说完美拟合了训练集的数据，而对训练集外的数据没有办法分辨。这个问题在深度学习上更加的突出，因为深度学习的拟合能力是更强的。防止过拟合可以正则化。简单地理解就是，通过加入一个正则项，在最小化新的代价函数的时候，正则项使得预测值与真实值之间的误差并不会达到最小，也就是说它是不会去完美拟合的，这样也就防止了过拟合，提高了机器学习模型的泛化能力。
参考文章：机器学习笔记之学习率（learning rate）与过拟合（overfitting）

下面对结果进行可视化：

import math

# 均匀生成40000个数据点
x1, x2 = torch.meshgrid(torch.linspace(-math.pi, math.pi, 200), torch.linspace(-math.pi, math.pi, 200))

x = torch.stack([torch.flatten(x1), torch.flatten(x2)], axis=1)

# 预测对应类别
y = runner.predict(x)
# y = torch.squeeze(torch.as_tensor(torch.can_cast((y>=0.5).dtype,torch.float32)))

# 绘制类别区域
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(x[:,0].tolist(), x[:,1].tolist(), c=y.tolist(), cmap=plt.cm.Spectral)

plt.scatter(X_train[:, 0].tolist(), X_train[:, 1].tolist(), marker='*', c=torch.squeeze(y_train,axis=-1).tolist())
plt.scatter(X_dev[:, 0].tolist(), X_dev[:, 1].tolist(), marker='*', c=torch.squeeze(y_dev,axis=-1).tolist())
plt.scatter(X_test[:, 0].tolist(), X_test[:, 1].tolist(), marker='*', c=torch.squeeze(y_test,axis=-1).tolist())

plt.show()

【思考题】对比3.1 基于Logistic回归的二分类任务 4.2 基于前馈神经网络的二分类任务，谈谈自己的看法。

逻辑回归可以看作是一个最简单的神经网络，理解逻辑回归对于理解神经网络的原理非常有帮助。二者都是基于最小化损失函数的思想，利用梯度下降法求导来更新权重参数w。但实际上求导过程中逻辑回归只需一步求导就行，而神经网络有若干个隐藏层，就是一个个加权求和再激活的嵌套，也就是链式求导。
此外，神经网络需要大样本才能显示出它灵活性的优点，即使已经有了大样本，只有真实回归函数不能由二次逻辑函数族逼近时，神经网络才会在模型选择过程中显示出其优越性。正如周志华老师对于多层前馈网络的表示能力的描述：只需要一个包含足够多神经元的隐层，多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数。

参考文章：前馈神经网络和Logit回归的比较研究

总结：模型性能评价的时候想起上回实验的拓展修改一下学习率和训练次数之类的，当时就是简单搜了一下大概该怎么改。这次搜了一下更深刻的了解了一下为啥要这么改，还挺有收获的。另外还学习到了个新概念仿射变换，通过看gif图更直观的了解了一下。

修正

将noise设置为0：

数据集可视化如图：
将noise设置为0.2：

出现比较确切的弯月数据集：

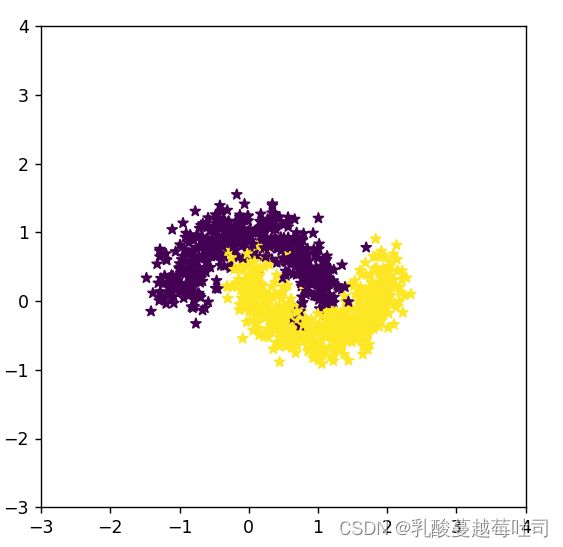
由于torch.normal()在加入高斯噪声的时候noise设置的过大，这会使得原本弯月数据集样本点过于分散，失去了数据集原本的”弯月“特征。