蒙特卡罗（Monte Carlo) 模拟

蒙特卡罗模拟（方法），也称为计算机随机模拟方法、统计模拟法、统计试验法，是基于”随机数“的计算方法，或者是说把概率现象作为研究对象的数值模拟方法。其数学基础是大数定律与中心极限定理。其基本思想是：为了求解问题，先建立一个概率模型或随机过程，再通过对过程的观察或抽样试验来计算参数或数字特征。最后求出解的近似值。

蒙特卡罗模拟求解实际问题的基本步骤：

（1）根据问题特点，构造概率统计模型，使所求的解是所求问题的概率分布或数学期望。

（2）给出模型中各种不同分布的随机变量的抽样方法。

（3）统计处理模拟结果，给出问题解的统计估计值和精确估计值。

蒙特卡罗（Monte Carlo)模拟实例 ：

（1）由概率计算事件发生频率

这个也是最基本的问题。例如，对于掷硬币，结果为正面和反面的概率各位0.5，那么掷100次硬币，有多少朝上面、多少朝下面呢？那么掷硬币1000次，10000次呢？

from random import random
n=1000 #掷硬币次数
s0=0 #累计正面出现的次数
s1=0 #累计反面出现的个数
for i in range(n):
    a=random() #产生0~1之间随机数，为概率分布为均匀分布
    if a<0.5:
        s0+=1
    elif a>=0.5:
        s1+=1
print(s0,s1)

以上就是兔兔模拟的1000次掷硬币的情况。第一次运行结果是499，501，已经很接近理论值500，500了。当次数越来越多，实际频率会逐渐靠近理论值的。随机数的产生，有非常多的方法。可以用random模块，也可以用numpy里面的random。

（2）求的近似值。

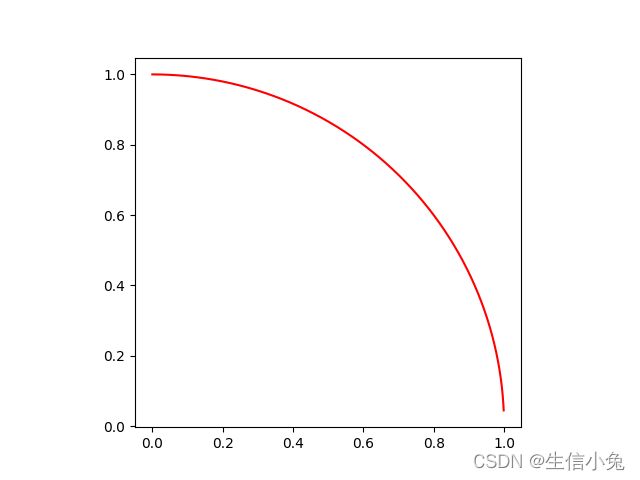
 对于这样边长为一的正方形，里面为半径为1的1/4圆。当我们往正方形内掷点时，由集合概率可知，落在圆内部的概率为。设总共投掷n个点，有m个点落在圆内。则,即。

from random import random
n=[100,1000,5000,10000]
pi=[]
for i in n:
    s=0
    for j in range(i):
        x=random()
        y=random()
        if x**2+y**2<1:
            s+=1
    pi.append(4*s/i)
print(pi)

兔兔运行结果是[3.36,3.072,3.1552,3.1484]。可以发现，随着试验次数的增加，实验值也逐渐接近于。

（3）求定积分值。

求定积分主要分为随机投点法与平均值（期望）法。随机投点法与前面类似，求函数在区间[a,b]的定积分，只要把这一部分放在一个包含它的矩形里面，那么落在函数包围里面的点与所有点的比值就是定积分值（函数曲线围成的面积）与矩形面积的比值，从而求出定积分的近似值。

对于平均值法，就不像前面那样直观了。它是在区间[a,b]内随机选x值，则由线y=0,y=f(x),x=a,x=b围成的矩形面积就是s=(a-b)*f(x),之后再随机选x,求面积s。随机选n次后，定积分值为。其思想类似于求函数在区间内的平均。

我们下面以函数y=sin(x)在区间内定积分为例。

from random import random
import math
s=0
for i in range(1000):
    x=random()*math.pi
    s+=math.pi*math.sin(x)
print(s/1000)

该定积分结果为2，模拟后兔兔的实验值是2.005564，已经很接近实际值了。

（4）求全局最优解（函数最值）。

关于求函数极值，就是在给定区间内随机产生若干个自变量的值搜索，找使得f(x)最大的那个x值。这种思想很像前面讲过的遗传算法与模拟退火算法中的一个部分。只不过这里更简单一些，就是随机大量的值，然后找最优的那一个。

（5）库存管理问题。

某小贩每天以a=2元/束的价格购进一种鲜花，卖价b=3元/束。花卖不出去则全部损失。顾客每天对花的需求X服从的泊松分布，。则小贩每天购多少鲜花才能得到好收益。

模拟求最优决策：购进鲜花个数u的算法步骤如下：

（1）对给定的a,b, (这里已知），进货量u(待求），收益为Mu。当u=0时，M0=0，再令u=1，继续下一步。

（2）对随机需求变量X做模拟，求出收入，共做n次模拟（即模拟卖花n天），求出收入的平均值Mu（卖花n天收入的平均值）。

（3）如果,令u=u+1;如果,则u=u-1。之后转到步骤（2）。

由于收益的值是随着u的增加先增后减（直观上可以体现），所以当收益减小时就可以让u退后一步，即u=u-1。收益增加时就继续让u往前，即u=u+1。

import numpy as np
a=2;b=3;lamda=10;M1=0
u=1;n=1000
for i in range(20):
    d=np.random.poisson(lamda,n) #产生n个数值，服从泊松分布
    M2=np.mean((b-a)*u*(u<=d)+((b-a)*d-a*(u-d)*(u>d)))
    if M2>M1:
        M1=M2
        u+=1
    elif M2

这里d是产生长度为n,服从泊松分布的数值，（u>d)或者（u<=d)判断d里面各个数值与u的关系，所以是一个值为True 和False 的数组。最终运行结果通常是8或9。

那么理论推导的u的最优解是多少呢？兔兔把推导过程写在下面了，结果为8或9。说明实验值与理论值很接近。

（6）排队问题。

某修理店有一个修理工，来修理的顾客先后到达时间间隔服从指数分布，平均间隔时间10min,对顾客服务时间（min）服从[4,15]均匀分布；顾客比较多时，一部分需要排队等待，排队按先到先服务顺序，队长无限制，顾客服务完便离开，一个工作日为8h(即480min)。

模拟2000个工作日完成服务个数及顾客平均等待时间。

关于这个问题。我们先从开始分析。假设修理店开门时刻是0，那么第一个顾客到达时刻为0+t0=c0,第二个顾客到达时刻为0+t0+t1=c0+t1=c2。其中的t是前后两个顾客到达的时间间隔，服从=10的指数分布，所以有递推公式：。

对于第一个顾客，到店后直接开始修理，所以等待时间w0=0。那么对于第二个顾客，如果他到达时第一个顾客已经走了，等待时间是0；如果第一个顾客还在修理，那么他的等待时间w1=c0+u0-c1=g0-c1。其中g0代表第一个顾客离开店的时刻，u0是第一个顾客修理的时间，服从[4,15]均匀分布。所以有递推公式：。g(k-1)是前一个顾客离开时刻，ck是后一个顾客到达时刻。

对于第一个顾客，他的离开时刻g0=c0+u0。那么对于下一个顾客，如果到达时c1>g0,即第一个顾客走了之后第二个顾客再来，则无需等待，离开时刻g1=c1+u1。如果到达时刻c1。g(k-1)代表前一个顾客离开时刻，ck是这个顾客到达时刻。

import numpy as np
p=0
s=0
for i in range(2000):
    W0=[0] #第一个顾客等待时间
    t0=np.random.exponential(10) #时间间隔
    c0=0+t0 #第一个顾客到达时刻
    u0=np.random.uniform(4,15)
    g0=c0+u0
    g=g0 #用来累计一天的工作时间
    while g<480:
        t=np.random.exponential(10) #下一个到达时间间隔
        u=np.random.uniform(4,15) #下一个服务时间
        c=c0+t #下一个到达时间
        w=max(0,g-c) #下一个等待时间
        g=max(g,c)+u #下一个离开时间
        c0=c #保存当前时刻
        W0.append(w) #保存顾客等待时间
    people=len(W0) #这一天服务人数
    time=np.mean(W0) #这一天人们平均等待时间
    p+=people
    t+=time
print('2000个工作日平均每日服务人数:',p/2000)
print('2000个工作日平均等待时间',t/2000)

 兔兔运行后，平均每日服务人数在43，44左右，平均等待时间0.02min附近。

总结

蒙特卡罗模拟本质还是利用随机数进行进行模拟计算。但同时也需要注意计算机产生的随机数其实也并不是真正的随机，相关实例兔兔在这里就不作展开了，在比较复杂的模拟的情况下是需要注意到这一点的。