现代循环神经网络-2.长短期记忆网络(LSTM)【动手学深度学习v2】

上一篇：现代循环神经网络-1.门控循环单元（GRU）【动手学深度学习v2】

2. 长短期记忆网络

长短期记忆网络的设计灵感来自于计算机的逻辑门。 长短期记忆网络引入了记忆元（memory cell），或简称为单元（cell）。 有些文献认为记忆元是隐状态的一种特殊类型， 它们与隐状态具有相同的形状，其设计目的是用于记录附加的信息。 为了控制记忆元，我们需要许多门。 其中一个门用来从单元中输出条目，我们将其称为输出门（output gate）。 另外一个门用来决定何时将数据读入单元，我们将其称为输入门（input gate）。 我们还需要一种机制来重置单元的内容，由遗忘门（forget gate）来管理， 这种设计的动机与门控循环单元相同， 能够通过专用机制决定什么时候记忆或忽略隐状态中的输入。

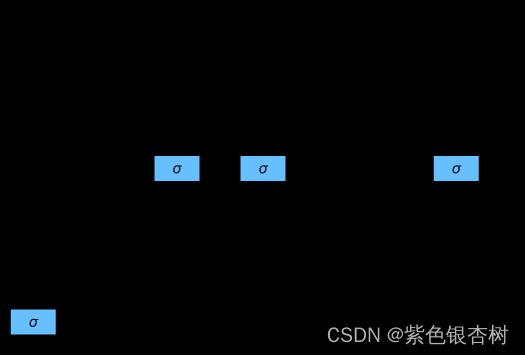
2.1 输入门、忘记门和输出门

长短期记忆单元与门控循环单元有相似的部分，其也是当前时间步的输入和前一个时间步的隐状态作为长短期记忆网络单元的输入，由三个具有sigmoid激活函数的全连接层处理， 以计算输入门、遗忘门和输出门，因此这些值都在(0,1)之内。

• 忘记门(forget gate)：将值朝0减少
• 输入门(input gate)：决定是不是忽略掉输入数据
• 输出门(output gate)：决定是不是使用隐藏状态

$$I_t=\sigma (X_t{W}_{xi}+H_{t-1}{W}_{hi}+b_i)$$
$$F_t=\sigma (X_t{W}_{xf}+H_{t-1}{W}_{hf}+b_f)$$
$$O_t=\sigma (X_t{W}_{xo}+H_{t-1}{W}_{ho}+b_o)$$

同理，$W_{\ast \ast }$是输入，输出，各种门之间的权重参数，$b_{\ast }$是偏置参数。

2.2 候选记忆元

候选记忆单元与上面的门计算类似，只有激活函数换成了tanh函数，因此候选记忆元的取值范围为(-1,1)。与GRU的两个门相比，LSTM的门数量增加到了4个。时间步为t时，候选记忆元的方程为：

$${\tilde{C}}_t=\tanh (X_t{W}_{xc}+H_{t-1}{W}_{hc}+b_c)$$

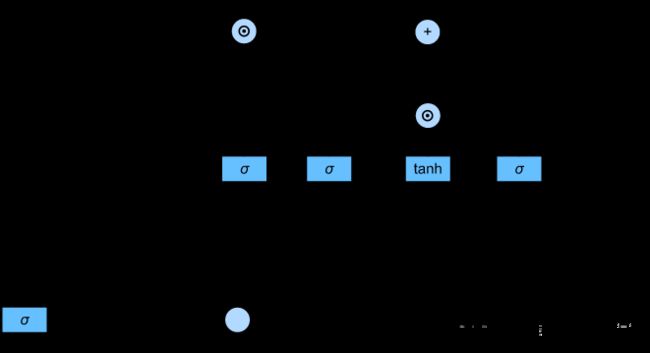
2.3 记忆单元

上一个记忆单元的状态会传入到本时刻的记忆单元，GRU中没有记忆单元传递影响。在长短期记忆网络中，当遗忘门趋向于0时，则由上一个记忆单元传送的信息将会被淡化或遗忘。如果输入门$I_t$为趋向1，则尽最大可能使用候选记忆单元，如果$I_t$趋向于0，则把现在的记忆单元的信息丢掉。与GRU不同的是，LSTM中$I_t$与$F_t$是独立影响记忆单元的，而GRU中的更新门$Z_t$对前后两个隐状态的影响是联系的。LSTM即可以要前面传递过来的记忆单元信息，也可以同时吸收当前的候选记忆单元信息。而GRU当前一个隐状态影响更大时，当前的候选隐状态影响就会更小。

$$C_t=F_t\odot C_{t-1}+I_t\odot {\tilde{C}}_t$$

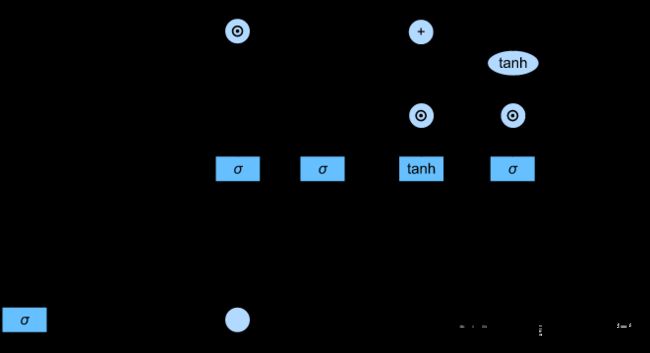
2.4 隐状态

记忆单元所得的值不一定在(-1,1)之间，因此在计算隐状态过程中，使用了tanh函数将$C_t$的值映射到(-1,1)之间。确保了$H_t$的值始终在区间(-1,1)内.

$$H_t=O_t\odot \tanh (C_t)$$

如果输出门趋向于零，隐状态也相当于被重置。

2.5 LSTM的代码实现

import torch
from torch import nn
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

def get_lstm_params(vocab_size, num_hiddens, device):
    num_inputs = num_outputs = vocab_size

    def normal(shape):
        return torch.randn(size=shape, device=device)*0.01

    def three():
        return (normal((num_inputs, num_hiddens)),
                normal((num_hiddens, num_hiddens)),
                torch.zeros(num_hiddens, device=device))

    W_xi, W_hi, b_i = three()  # 输入门参数
    W_xf, W_hf, b_f = three()  # 遗忘门参数
    W_xo, W_ho, b_o = three()  # 输出门参数
    W_xc, W_hc, b_c = three()  # 候选记忆元参数
    # 输出层参数
    W_hq = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    # 附加梯度
    params = [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc,
              b_c, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params

def init_lstm_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device),
            torch.zeros((batch_size, num_hiddens), device=device))

def lstm(inputs, state, params):
    [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,
     W_hq, b_q] = params
    (H, C) = state
    outputs = []
    for X in inputs:
        I = torch.sigmoid((X @ W_xi) + (H @ W_hi) + b_i)
        F = torch.sigmoid((X @ W_xf) + (H @ W_hf) + b_f)
        O = torch.sigmoid((X @ W_xo) + (H @ W_ho) + b_o)
        C_tilda = torch.tanh((X @ W_xc) + (H @ W_hc) + b_c)
        C = F * C + I * C_tilda
        H = O * torch.tanh(C)
        Y = (H @ W_hq) + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H, C)

vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_lstm_params,
                            init_lstm_state, lstm)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

perplexity 1.3, 22457.5 tokens/sec on cuda:0
time traveller came back andfilby s anecofo cennom think so i gh
traveller but becan his of the incitan velines abyout his f

2.6 LSTM的简洁实现

num_inputs = vocab_size
lstm_layer = nn.LSTM(num_inputs, num_hiddens)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)