【动手学习pytorch笔记】25.长短期记忆LSTM
LSTM
理论
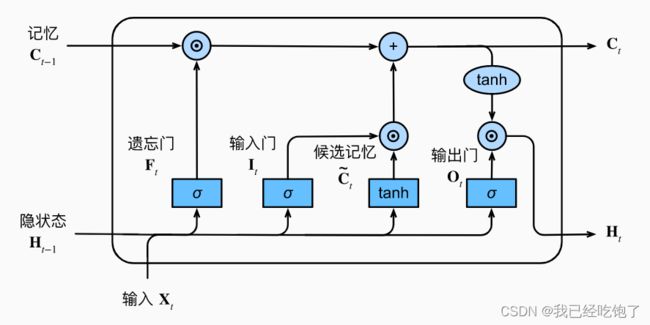
输入门(决定是否适用隐藏状态) I t = σ ( X t W x i + H t − 1 W h i + b i ) I_t = \sigma(X_tW_{xi}+H_{t-1}W_{hi}+b_i) It=σ(XtWxi+Ht−1Whi+bi)
遗忘门(将值朝0减少) F t = σ ( X t W x f + H t − 1 W h f + b f ) F_t = \sigma(X_tW_{xf}+H_{t-1}W_{hf}+b_f) Ft=σ(XtWxf+Ht−1Whf+bf)
输出门(决定是否适用隐藏状态) O t = σ ( X t W x o + H t − 1 W h o + b o ) O_t = \sigma(X_tW_{xo}+H_{t-1}W_{ho}+b_o) Ot=σ(XtWxo+Ht−1Who+bo)
候选记忆单元(这不就是RNN的H么) C t ~ = t a n h ( X t W x c + H t − 1 W h c + b c ) \tilde{C_t} =tanh(X_tW_{xc}+ H_{t-1}W_{hc}+b_c) Ct~=tanh(XtWxc+Ht−1Whc+bc)
记忆单元 C t = F t ⋅ C t − 1 + I t ⋅ C t ~ C_t =F_t \cdot C_{t-1} + I_t \cdot \tilde{C_t} Ct=Ft⋅Ct−1+It⋅Ct~
隐藏状态 H t = O t ⋅ t a n h ( C t ) H_t =O_t \cdot tanh(C_t) Ht=Ot⋅tanh(Ct)
LSTM的记忆单元和和GRU的记忆单元相比,上一步 C t − 1 C_{t-1} Ct−1和这一步 C t ~ \tilde{C_t} Ct~都可以有权重,不像GRU是 Z 和 (1-Z),当然也可以都没有。
隐藏状态 t a n h ( C t ) tanh(C_t) tanh(Ct)是因为 C t C_t Ct是[-2, 2],要重新变回[-1, 1]
输出门如果是0,意味着当前的 H t H_t Ht和之前的信息都不要了,下一个时序看到的是和之前完全无关的
代码
import torch
from torch import nn
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
def get_lstm_params(vocab_size, num_hiddens, device):
num_inputs = num_outputs = vocab_size
def normal(shape):
return torch.randn(size=shape, device=device)*0.01
def three():
return (normal((num_inputs, num_hiddens)),
normal((num_hiddens, num_hiddens)),
torch.zeros(num_hiddens, device=device))
W_xi, W_hi, b_i = three() # 输入门参数
W_xf, W_hf, b_f = three() # 遗忘门参数
W_xo, W_ho, b_o = three() # 输出门参数
W_xc, W_hc, b_c = three() # 候选记忆元参数
# 输出层参数
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
# 附加梯度
params = [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc,
b_c, W_hq, b_q]
for param in params:
param.requires_grad_(True)
return params
def init_lstm_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device),
torch.zeros((batch_size, num_hiddens), device=device))
turple终于又用了,这里一个C一个H
def lstm(inputs, state, params):
[W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,
W_hq, b_q] = params
(H, C) = state
outputs = []
for X in inputs:
I = torch.sigmoid((X @ W_xi) + (H @ W_hi) + b_i)
F = torch.sigmoid((X @ W_xf) + (H @ W_hf) + b_f)
O = torch.sigmoid((X @ W_xo) + (H @ W_ho) + b_o)
C_tilda = torch.tanh((X @ W_xc) + (H @ W_hc) + b_c)
C = F * C + I * C_tilda
H = O * torch.tanh(C)
Y = (H @ W_hq) + b_q
outputs.append(Y)
return torch.cat(outputs, dim=0), (H, C)
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_lstm_params,
init_lstm_state, lstm)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
perplexity 1.1, 19744.0 tokens/sec on cuda:0
time traveller for so it will be convenient to speak of himwas e
travellerbut becarfally but s i the peosterto timey itwing
简易实现
num_inputs = vocab_size
lstm_layer = nn.LSTM(num_inputs, num_hiddens)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
perplexity 1.0, 132211.4 tokens/sec on cuda:0
time travelleryou can show black is white by argument said filby
travelleryou can show black is white by argument said filby