机器学习之聚类
入门小菜鸟,希望像做笔记记录自己学的东西,也希望能帮助到同样入门的人,更希望大佬们帮忙纠错啦~侵权立删。
目录
一、聚类介绍
二、聚类性能度量
1、分类
2、符号假设
3、外部指标
(1)Jaccard系数(JC)
(2)FM指数(FMI)
(3)Rand指数(RI)
4、有关簇的距离的定义
(1)簇C内样本间的平均距离
(2)簇C内样本间的最远距离
(3)簇编辑与簇编辑最近样本间的距离
(4)簇编辑与簇编辑中心点间的距离
5、内部指标
(1)DB指数(DBI)
(2)Dunn指数(DI)
5、实际场景中的聚类分数定义
(1)SSE—误差平方和
(2)轮廓系数法
(3)Calinski-Harbasz Score(CH)
三、距离度量
1、闵可夫斯基距离
(1)欧氏距离(p=2)
(2)曼哈顿距离(p=1)
(3)切比雪夫距离(p=无穷)
2、VDM
3、MinkovDM距离
4、加权距离
四、原型聚类
1、k-means聚类
(1)算法思想
(2)算法步骤
(3)k值选择
(4)python实现k-means算法
(5)优缺点
2、学习向量量化(LVQ)
(1)算法思想
(2)算法步骤
(3)python实现LVQ
(4)优缺点
3、高斯混合聚类
(1)算法思想与推导
(2)算法步骤
(3)优缺点
4、密度聚类
(1)DBSCAN算法思路
(2)DBSCAN算法步骤
(3)DBSCAN的python实现
(4)DBSCAN优缺点
5、层次聚类
(1)AGNES算法思路
(2)AGNES算法步骤
(3)AGNES的python实现
(4)AGNES优缺点
一、聚类介绍
无监督学习中最常见的即为聚类学习。
聚类学习是按照某种特定标准(如距离等)把一个数据集划分为不同的类或簇(子集),使得同一个簇内的数据对象的相似性尽可能大,不在同一个簇中的数据对象的差异性也尽可能地大(即聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离)。这些划分后的概念对于聚类算法而言是未知的,簇所对应的概念语义需要我们自行接着探索,所以经常聚类被用作分类等其他学习任务的前驱过程。
二、聚类性能度量
整体希望簇内相似度高,簇间相似度低。
1、分类
聚类性能度量分为两类:
一类是将聚类结果与某个“参考模型”进行比较,称为“外部指标”;
一类是直接考察聚类结果而不利用任何参考模型,称为“内部指标”。
2、符号假设
数据集![]() ;聚类得到的簇划分为
;聚类得到的簇划分为![]() ;参考模型给出的簇划分为
;参考模型给出的簇划分为![]() ;相应的,
;相应的,![]() 与
与 ![]() 分别为
分别为 ![]() 和
和 ![]() 对应的簇标记向量。
对应的簇标记向量。
将样本两两配对考虑,得:
![]()
![]()
![]()
![]()
那么有![]() ;m为样本总数。
;m为样本总数。
3、外部指标
(1)Jaccard系数(JC)
![]() ,取值为[0,1]。
,取值为[0,1]。
意义:在所有判定为同一类中,两种方法都判定为同一类的比例。
用于比较聚类结果与参考模型得出的结果之间的相似性与差异性。Jaccard系数值越大,两者的相似度越高。
JC的原始定义:(其中A,B是两个不同的集合)
![]()
(2)FM指数(FMI)
从两者预测的准确率的角度入手,进行对比。值越大说明两者的预测越接近,相似度越高。
(3)Rand指数(RI)
描述两种方法都判定相同在所有预测中的占比,值越大,相似度越高。
4、有关簇的距离的定义
(1)簇C内样本间的平均距离
(2)簇C内样本间的最远距离
![]()
(3)簇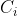 与簇
与簇 最近样本间的距离
最近样本间的距离
![]()
(4)簇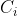 与簇
与簇 中心点间的距离
中心点间的距离
![]()
其中,u代表簇的中心点。
5、内部指标
(1)DB指数(DBI)
其意义为:任意两个簇的簇内平均距离之和与它们簇中心间距离的比值的最大值。
值越小,代表聚类结果的簇间距离越大,而簇内距离越小。
(2)Dunn指数(DI)
值越大,簇间距离越大,簇内距离越小。
5、实际场景中的聚类分数定义
(1)SSE—误差平方和
每类中的点到对应簇中心的欧氏距离平方的和 ,值越小,聚类效果越好
只体现了衡量簇内样本的距离远近。
(2)轮廓系数法
该方法结合了聚类的凝聚度和分离度
a(i):样本 i 到所有它属于的同一簇中其它点的距离的平均值,称为凝聚度;
b(i):样本 i 到所有它不属于的簇内所有点的平均距离的最小值,称为分离度;
样本i的轮廓系数为:
![]()
取值为[-1,1],越接近1聚类效果越好(即簇内样本的距离越近,簇间样本距离越远)。
对于衡量整个聚类体系,则采取取所有点的轮廓系数的平均值。
同时考虑到簇内/簇间距离远近。
(3)Calinski-Harbasz Score(CH)
它是通过评估类之间方差和类内方差来计算得分的。
![]()
其中k代表聚类类别数,N代表全部数据数目。![]() 是类间方差矩阵,
是类间方差矩阵,![]() 是类内方差矩阵。
是类内方差矩阵。
三、距离度量
在聚类中,距离被当作一种描述相似度大小的工具,距离越大,相似度越小。相似度度量距离是“非度量距离”(不满足直递性)。
1、闵可夫斯基距离
适用于有序属性。
其中p>=1。
(1)欧氏距离(p=2)
表明的是空间点间的最短距离。
十分适合低维数据
缺点:尽管他很常用,但欧式距离并不是尺度不变的,这意味着所计算的距离可能会根据特征的单位发生倾斜。通常,在使用欧式距离度量之前,需要对数据进行归一化处理。此外,随着数据维数的增加,欧氏距离的作用也就越小。这与维数灾难有关。
(2)曼哈顿距离(p=1)
![]()
表明的是两个点在标准坐标系上的绝对轴距总和。
缺点:尽管曼哈顿距离在高维数据中似乎可以工作,但它比欧式距离直观性差,尤其是在高维数据中使用时。
(3)切比雪夫距离(p=无穷)
若在二维空间中则被简化为:
![]()
切比雪夫距离定义为两个向量在任意坐标维度上的最大差值。换句话说,它就是沿着一个轴的最大距离。
缺点:切比雪夫距离通常用于特定的用例(比如一个方块移动到另一个方块所需的最小移动次数),这使得它很难像欧氏距离或余弦相似度那样作为通用的距离度量。
2、VDM
该距离针对于无序属性(比如:{飞机,火车,汽车}),不能简单的转化为{1,2,3},因为原先的属性间没有明显的大小远近等“序”的关系,而是转化为向量处理,比如转化为{[1,0,0],[0,1,0],[0,0,1]}。
描述属性u上两个离散值a与b间的距离
其中![]() 表示在属性u上取值为a的样本数;
表示在属性u上取值为a的样本数;![]() 表示在第i个样本簇中在属性u上取值为a的样本数;k为样本簇数。
表示在第i个样本簇中在属性u上取值为a的样本数;k为样本簇数。
3、MinkovDM距离
针对混合属性(有序+无序)
即将闵可夫斯基距离和VDM结合在一起,令有序属性排列在无序属性之前,则有
其中有序属性个数为![]() ,无序属性个数为
,无序属性个数为![]() 。
。
4、加权距离
上述的方法都是基于对于每个属性而言重要性一致,但是有些情况下我们可以获悉哪些属性权重更大,哪些更小,因此可以对于不同属性进行加权处理以作距离度量。
四、原型聚类
1、k-means聚类
(1)算法思想
k-means算法属于无监督学习。
补:
监督学习:输入的数据有标签;
无监督学习:输入的数据没有标签;
K-Means聚类算法是一种迭代求解的聚类分析算法。
算法思想是:我们需要随机选择K个对象作为初始的聚类中心,然后计算每个对象和各个聚类中心之间的距离,然后将每个对象分配给距离它最近的聚类中心。聚类中心及分配给它们的对象就代表着一个聚类。每分配一个样本,聚类的中心会根据聚类中现有的对象被重新计算。此过程将不断重复,直至满足设置的终止条件。
(2)算法步骤
A. 首先需要随机初始化k个聚类中心![]() (其中,n为样本数)
(其中,n为样本数)
B. 然后通过计算每一个样本到每一个聚类中心的欧式距离,如下式所示:
其中,
表示第i个样本;
表示第j个聚类中心;
表示第i个样本的第t个属性;
表示第j个聚类中心的第t个属性,m为属性种类数。
C. 然后依次比较每个样本到每一个聚类中心的距离,将样本分配到距离最近的聚类中心的类簇中,得到k个类簇![]()
D. 根据不同的类簇,更新每个类簇的聚类中心,计算公式如下:
其中:
表示第t个聚类的中心;
表示第t个类簇中样本的个数;
表示第t个类簇中第i个样本。
E. 重复步骤B到D,直至聚类中心不再改变或者改变幅度很小(新计算出来的质心和原来的质心之间的距离小于某一个设置的阈值),得到最终的聚类结果。
(3)k值选择
k值决定了将数据划分成多少个簇类。k个初始化的质心的位置选择对最后的聚类结果和整个大代码的运行时间都有非常大的影响。因此需要选择合适的k个质心
一般k值是通过先验知识来选取的。如果没有什么先验知识,我们可以通过交叉验证的方式来选择一个合适的k值
(4)python实现k-means算法
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs#为了生成数据集
from sklearn.cluster import KMeans
# X为样本特征,共1000个样本,每个样本2个特征,对应x和y轴,共2个簇,
# 簇中心在[-1,-1],[1,1], 簇方差分别为[0.4,0.8]
X, _ = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [1, 1]],
cluster_std=[0.4, 0.8], random_state=4)
#k-means算法聚类分类结果
y_pred = KMeans(n_clusters=2, random_state=9).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()结果:
![]()
注:如果非二,三维数据,无法可视化,可以采取将预测的簇标签输出,再以这些标签来反推簇的性质。
(5)优缺点
A、优点
- 原理简单,易实现
- 可解释度较强
B、缺点
- K值难以确定
- 局部最优
- 对噪声点和异常点敏感
- 要求样本存在均值的意义(限定数据种类,比如说:一些性质的有无就不太好用这个方法,难以表示)
- 聚类效果依赖于聚类中心的初始化
- 对于非凸数据集或类别规模差异太大的数据效果不好(见下面与密度聚类的对比)
2、学习向量量化(LVQ)
(1)算法思想
LVQ与一般聚类算法思路类似,只是LVQ假设数据样本带有类别标记,学习过程利用样本的这些监督信息来辅助聚类。
(2)算法步骤
A、输入数据集:![]() ,原型向量个数为q,各原型向量预设的类别标记
,原型向量个数为q,各原型向量预设的类别标记![]() ,学习率为
,学习率为![]() ;
;
B、初始化一组原型向量![]() ;
;
C、从样本集D随机选取样本![]() ,计算样本
,计算样本![]() 与
与![]() 的距离:
的距离:![]() ;
;
D、找出与![]() 距离最近的原型向量
距离最近的原型向量![]() ,
,![]() ;
;
E、如果![]() ,那么
,那么![]() ;否则,
;否则,![]() ,将原型向量
,将原型向量![]() 更新为
更新为![]() ;
;
F、重复C到E步骤,直至满足停止条件,输出原型向量![]()
(3)python实现LVQ
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn_lvq import LgmlvqModel
iris = datasets.load_iris()
x = iris.data
y = iris.target
train_x,test_x,train_y,test_y = train_test_split(x,y,test_size=0.3,random_state=0)
model = LgmlvqModel()
model.fit(train_x,train_y)
pred = model.predict(test_x)
acc = accuracy_score(test_y, pred)
print(acc)结果:
![]()
(4)优缺点
与k-means类似。
3、高斯混合聚类
(1)算法思想与推导
高斯混合聚类采用概率模型来表述聚类原型。
多元高斯分布
其中,![]() 为n维均值向量;
为n维均值向量;![]() 为随机变量X的协方差矩阵(n*n);
为随机变量X的协方差矩阵(n*n);
而它由![]() 这两个参数决定,因此把
这两个参数决定,因此把![]() 写作
写作![]() 。
。
高斯混合分布
该分布共由k个混合成分组成,每个混合成分对应一个高斯分布。其中![]() 与
与![]() 是第i个高斯混合成分的参数, 而
是第i个高斯混合成分的参数, 而![]() 为相应的 “混合系数”,且
为相应的 “混合系数”,且 
由高斯混合分布给出的样本的生成过程:
首先根据
定义的先验分布选择高斯混合分布,其中
是选择第i个混合成分的概率;
然后根据被选择的混合成分的概率密度函数进行采样,从而生成相应的样本。
假设数据分布是由高斯混合分布生成——不同的混合成分即不同的簇
若训练集![]() 由上述的高斯混合分布给出的样本过程生成,令随机变量
由上述的高斯混合分布给出的样本过程生成,令随机变量![]() 表示生成样本
表示生成样本![]() 的高斯混合成分,但未知其取值。根据贝叶斯定理可得样本
的高斯混合成分,但未知其取值。根据贝叶斯定理可得样本![]() 由第i个高斯混合成分生成的后验概率如下:
由第i个高斯混合成分生成的后验概率如下:
所以根据上面的后验概率来推测该样本是由哪个高斯混合成分生成的,即属于哪个簇。每个样本![]() 的簇标记
的簇标记![]() 为:
为: ![]()
极大似然法求解模型参数:![]()
命求导为0,可得:
对于混合系数![]() :
:
除了要最大化LL(D),还需要满足 ,所以有LL(D)的拉格朗日形式:
,所以有LL(D)的拉格朗日形式:
(2)算法步骤
A、设置k的个数(即初始化高斯混合模型的成分个数),并且随机初始化每个簇的高斯分布参数(均值和方差)或者观察数据给出一个相对精确的均值和方差。
B、计算每个数据点属于每个高斯模型的概率,即计算后验概率(点越靠近高斯分布的中心,则概率越大,即属于该簇可能性更高)
C、计算 α,μ,Σ 参数使得数据点的概率最大化,使用数据点概率的加权来计算这些新的参数,权重即为数据点属于该簇的概率。
D、重复B与C直到EM算法停止条件满足(eg:达到最大迭代次数,达到收敛)。
(3)优缺点
A、优点
只要给定的成分个数足够多,理论上可以任意逼近任何连续的概率分布,理论上都是符合要求的
B、缺点
-
计算量大
-
真实数据很多不服从正态分布,对于一些复杂数据可能会出现偏差。
4、密度聚类
密度聚类能通过样本分布的紧密程度确定,通常情况下考察样本间的可连接性并基于可连接样本不断扩展聚类簇以获取最终聚类结果。常见的密度聚类算法是DBSCAN。
(1)DBSCAN算法思路
基于一组“邻域”参数来刻画样本分布的紧密程度。
定义数据集 ![]() ,有以下几个概念:
,有以下几个概念:
 -邻域:对于
-邻域:对于 ,其ϵ-邻域包含样本集D中与
,其ϵ-邻域包含样本集D中与 的距离不大于ϵ的样本集,即
的距离不大于ϵ的样本集,即
- 核心对象:若
 的
的 -邻域至少包含MinPts个样本,即如果
-邻域至少包含MinPts个样本,即如果 ,则
,则 是核心对象
是核心对象 - 密度直达:如果
 位于
位于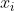 的ϵ-邻域中,且
的ϵ-邻域中,且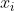 是核心对象,则称
是核心对象,则称 由
由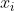 密度直达(若两个都是核心对象,则看谁的
密度直达(若两个都是核心对象,则看谁的 -邻域内的样本多
-邻域内的样本多 - 密度可达:对于
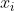 和
和 ,如果存在样本样本序列
,如果存在样本样本序列 ,其中
,其中 且
且 由
由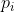 密度直达,则称
密度直达,则称 由
由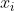 密度可达。也就是说,密度可达满足传递性。此时序列中的传递样本
密度可达。也就是说,密度可达满足传递性。此时序列中的传递样本 均为核心对象,因为只有核心对象才能使其他样本密度直达。注意密度可达也不满足对称性(由密度直达的不对称性可得)
均为核心对象,因为只有核心对象才能使其他样本密度直达。注意密度可达也不满足对称性(由密度直达的不对称性可得) - 密度相连:对于
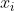 和
和 ,如果存在核心对象样本
,如果存在核心对象样本 ,使
,使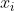 和
和 均由
均由 密度可达,则称
密度可达,则称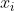 和
和 密度相连(密度相连关系满足对称性)
密度相连(密度相连关系满足对称性)
DBSCAN中的簇:由密度可达关系导出的最大的密度相连样本集合。即给定邻域参数(![]() ,MinPts)
,MinPts)
,簇内元素满足连接性(簇内样本彼此样本密度相连)和最大性(由簇内元素密度可达的元素也属于该簇)
(2)DBSCAN算法步骤
输入:数据集![]() ,邻域半径
,邻域半径![]() ,邻域中数据对象数目阈值MinPts;
,邻域中数据对象数目阈值MinPts;
A、从未被归类到簇中的数据集中任意选取一个数据对象点 p;
B、如果对于参数 ![]() 和 MinPts,所选取的数据对象点 p 为核心对象,则找出所有从 p 密度可达的数据对象点,形成一个簇;
和 MinPts,所选取的数据对象点 p 为核心对象,则找出所有从 p 密度可达的数据对象点,形成一个簇;
C、如果选取的数据对象点 p 是边缘点,选取另一个数据对象点;
D、重复B、C步,直到所有点被处理。
输出:密度联通簇。
补:若有先设置簇的个数k,则在步骤B改为随机选取k个数据对象点,其余步骤类似。
(3)DBSCAN的python实现
from sklearn.cluster import DBSCAN
from sklearn.cluster import KMeans
from sklearn.datasets import make_circles
import matplotlib.pylab as plt
#DBSCAN
x,y=make_circles(n_samples=3000,factor=0.3,noise=0.05)
y_pred2 = DBSCAN(eps=0.2).fit_predict(x)
plt.scatter(x[:,0],x[:,1],c=y_pred2)
plt.show()
#对应k-means,进行对比
model1 = KMeans(n_clusters=2)
y_pred = model1.fit_predict(x)
plt.scatter(x[:,0],x[:,1],c=y_pred)
plt.show()结果:
(1)DBSCAN
(2)k-means
(4)DBSCAN优缺点
A、优点
- 可以对任意形状的稠密数据集进行聚类(对比k-means);
- 可以在聚类的同时发现异常点,对数据集中的异常点不敏感;
- 不需要指定簇数,并且多次实验结果往往是相同的;
B、缺点
- 不适合密度不均匀、聚类间距差相差很大的样本集;
- 调参相较于K-Means复杂一点(半径与个数),不同参数组合对聚类效果有很大影响;
- 由于传统的欧式距离不能很好处理高纬数据,所以对于距离定义较难给出好的解决方案;
- 当不同簇的密度变化很大时会出现一些问题(比如:很容易把一些数据点标记为噪声);
5、层次聚类
在不同层次对数据集进行划分,从而形成树形的聚类结构。数据集的划分采用“自底向上”或“自顶向下”的拆分策略。AGNES(凝聚层次聚类)采用自底向上聚合策略。
(1)AGNES算法思路
首先设定一个期望的分类数目n,一开始把每个数据样本都分别看成一个类,然后计算所有类之间两两的距离,找出距离最短的两个类,并把这两个类合并为一个类,到此则总类数减1。接着再重复上述过程:计算所有类之间两两的距离,找出距离最短的两个类,并把这两个类合并为一个类。以此类推,类总数逐渐减少,直到类总数减少到n为止,则停止分类。
距离度量:
(2)AGNES算法步骤
A、先将数据集中的每个样本看作一个初始聚类簇;
B、然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并;
C、步骤B不断重复,直至达到预设的聚类簇的个数。
(3)AGNES的python实现
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import AgglomerativeClustering
from sklearn import datasets
from sklearn.metrics import confusion_matrix
iris=datasets.load_iris()
irisdata=iris.data
clustering=AgglomerativeClustering(linkage='ward',n_clusters=3)
clustering=clustering.fit(irisdata)
print("每个簇的样本数目:")
print(pd.Series(clustering.labels_).value_counts())
print("聚类结果:")
print(confusion_matrix(iris.target,clustering.labels_))
plt.figure()
d0=irisdata[clustering.labels_==0]
plt.plot(d0[:,0],d0[:,1],'r.')
d1=irisdata[clustering.labels_==1]
plt.plot(d1[:,0],d1[:,1],'g.')
d2=irisdata[clustering.labels_==2]
plt.plot(d2[:,0],d2[:,2],'b.')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.show()结果:
![]()
![]()
(4)AGNES优缺点
A、优点
适用于任意形状和任意属性的数据集;
可以灵活控制不同层次的聚类粒度,强聚类能力
B、缺点
算法的执行时间长;
不能回溯处理;
欢迎大家在评论区批评指正,谢谢














