吴恩达机器学习-K-means/降维
- K- 均值
-
- K- 均值算法
- 优化目标
- 随机初始化
- 选择聚类数
- 降维
-
- 动机一:数据压缩
- 动机二:数据可视化
- 主成分分析问题
- 主成分分析算法
- 选择主成分的数量
- 重建的压缩表示
- 主成分分析法的应用建议
K- 均值
K- 均值算法
非监督学习中,我们的数据没有附带任何标签y,数据就是这样的

我们需要将一系列无标签的训练数据,输入到一个算法中,然后我们告诉这个算法,快去为我们找找这个数据的内在结构给定数据。我们可能需要某种算法帮助我们寻找一种结构。图上的数据看起来可以分成两个分开的点集(称为簇),一个能够找到我圈出的这些点集的算法,就被称为聚类算法
K- 均值是最普及的聚类算法,算法接受一个未标记的数据集,然后将数据聚类成不同的组。
K- 均值是一个迭代算法,假设我们想要将数据聚类成 n 个组,其方法为:
-
首先选择K个随机的点,称为聚类中心 聚类中心(cluster centroids);
如图所示,选取红× 和 蓝×

-
对于数据集中的每一个数据,按照距离K个中心点的距离,将其与距离最近的中心点关
联起来,与同一个中心点关联的所有点聚成一类。

-
计算每一个组的平均值,将该组所关联的中心点移动到平均值的位置。

重复步骤 2-3 直至中心点不再变化

用u1 ,u 2 ,…,u k来表示聚类中心的位置,用c(1) ,c (2) ,…,c(m) 来存储与第i个实例数据最近的聚类中心的索引,K- 均值算法的伪代码
Repeat {
for i = 1 to m
c(i) := index (form 1 to K) of cluster centroid closest to x(i)
for k = 1 to K
μk := average (mean) of points assigned to cluster k
}
算法分为两个步骤,
第一个 for 循环是赋值步骤,即:对于每一个样例i,计算其应该属于的类。
第二个 for 循环是聚类中心的移动,即:对于每一个类K,重新计算该类的质心。
K- 均值算法也可以很便利地用于将数据分为许多不同组,即使在没有非常明显区分的组群的情况下也可以。下图所示的数据集包含身高和体重两项特征构成的,利用 K- 均值算法将数据分为三类,用于帮助确定将要生产的 T-恤衫的三种尺寸

优化目标
K-均值最小化问题,是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和,
因此 K-均值的代价函数(又称 畸变函数 Distortion function)为:

细化说
第一步中,最小化选c(1) ,c (2) ,…,c(m) ,第二步中,最小化选u1 ,u 2 ,…,u k

随机初始化
在运行 K- 均值算法的之前,我们首先要随机初始化所有的聚类中心点,下面介绍怎样
做:
- 我们应该选择K < m,即聚类中心点的个数要小于所有训练集实例的数量
- 随机选择K个训练实例,然后令K个聚类中心分别与这K个训练实例相等
K- 均值的一个问题在于,它有可能会停留m在一个局部最小值处,而这取决于初始化的情况
为了解决这个问题,我们通常需要多次运行 K- 均值算法,每一次都重新进行随机初始化,最后再比较多次运行 K-均值 均值的结果,选择代价函数最小的结果。这种方法在K较小的时
候(2–10)还是可行的,但是如果K较大,这么做也可能不会有明显地改善
选择聚类数
没有所谓最好的选择聚类数的方法,通常是需要根据不同的问题,人工进行选择的。选择的时候思考我们运用 K- 均值算法聚类的动机是什么,然后选择能最好服务于该目的标聚类数。
当人们在讨论,选择聚类数目的方法时,有一个可能会谈及的方法叫作 “肘部法则” 。关
于“肘部法则”,我们所需要做的是改变K值,也就是聚类类别数目的总数。我们用一个聚类
来运行 K 均值聚类方法。这就意味着,所有的数据都会分到一个聚类里,然后计算成本函数或者计算畸变函数J。K代表聚类数字。

我们可能会得到左面图中一条类似于这样的曲线。像一个人的肘部。这就是“肘部法则”所做的,你会发现这种模式,它的畸变值会迅速下降,从 1 到 2,从 2 到 3 之后,你会在 3 的时候达到一个肘点。在此之后,畸变值就下降的非常慢,使用 3 个聚类来进行聚类是正确的.
降维
动机一:数据压缩
数据压缩不仅允许我们压缩数据,因而使用较少的计算机内存或磁盘空间,但它也让我们加快我们的学习算法。
2D到1D:

从三维降至二维:
动机二:数据可视化
假使我们有有关于许多不同国家的数据,每一个特征向量都有 50 个特征(如 GDP,人均GDP,平均寿命等)。如果要将这个 50 维的数据可视化是不可能的。使用降维的方法将其降至 2 维,我们便可以将其可视化了。
这样做的问题在于,降维的算法只负责减少维数,新产生的特征的意义就必须由我们自己去发现了。
主成分分析问题
主成分分析(PCA)是最常见的降维算法。
在 PCA 中,我们要做的是找到一个方向向量(Vector direction),当我们把所有的数据都投射到该向量上时,我们希望投射平均均方误差能尽可能地小。方向向量是一个经过原点的向量,而投射误差是从特征向量向该方向向量作垂线的长度(图中蓝线)。
主成分分析问题的描述:
问题是要将n维数据降至k维,目标是找到向量u(1) ,u (2) ,…,u (k) 使得总的投射误差最小。

主成分分析与线性回归是两种不同的算法。
主成分分析最小化的是投射误差(ProjectedError),而线性回归尝试的是最小化预测误差。线性回归的目的是预测结果y,而主成分分析不作任何预测(无y,只有x)。

上图中,左边的是线性回归的误差(垂直于横轴投影),右边则是主要成分分析的误差(垂直于红线投影)
主成分分析算法
PCA 减少n维到k维:

2 第二步是计算协方差矩阵 协方差矩阵(covariance matrix)
在 Octave 里我们可以利用 奇异值分解(singular value decomposition)来求解, [U, S,V]= svd(sigma) 。
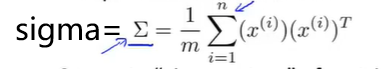
3 得到 n × n维度的矩阵U之后,如果我们希望将数据从n维降至k维,我们只需要从U中选取前k个向量,获得一个n × k维度的矩阵,我们用U(reduce) 表示,然后通过如下计算获得要求的新特征向量z(i) :
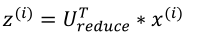
其中x是n × 1维的,因此结果为k × 1维度,如图

选择主成分的数量
14-5带翻译视频链接: https://www.bilibili.com/video/av95751735spm_id_from=333.788.b_636f6d6d656e74.80.
主要成分分析是减少投射的平均均方误差,两个方法选k值
第1种.
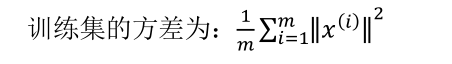
我们希望在平均均方误差与训练集方差的比例尽可能小的情况下选择尽可能小的k值。如果我们希望这个比例小于 1%,就意味着原本数据的偏差有 99%都保留下来了,如果我们选择保留 95%的偏差,便能非常显著地降低模型中特征的维度了。我们可以先令k = 1,然后进行主要成分分析,获得U(reduce) 和z,然后计算比例是否小于1%。如果不是的话再令k = 2,如此类推,直到找到可以使得比例小于 1%的最小k值(原因k是各个特k征之间通常情z况存在某种相关性)
第2种

重建的压缩表示
给定的z (i) ,怎么回到你原来的表示x (i) ?
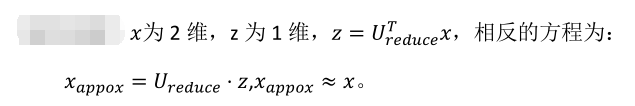

主成分分析法的应用建议

错误的主要成分 分析情况:一个常见错误使用主要成分分析的情况是, 将其用于减少过拟合(减少了特征的数量)。这样做非常不好,不如尝试正则化处理。 原因在于主要成分分析只是近似地丢弃掉一些特征,它并不考虑任何与结果变量有关的信息,因此可能会丢失非常重要的特征。然而当我们进行正则化处理时,会考虑到结果变量,不会丢掉重要的数据。
另一个常见的错误是,默认地将主要成分分析作为学习过程中的一部分,这虽然很多时候有效果,最好还是从所有原始特征开始,只在有必要的时候(算法运行太慢或者占用太多内存)才考虑采用主要成分分析。