高精度计算--高精度加法详解

---

前言

利用计算机进行数值计算，有时会遇到这样的问题：有些计算要求精度高，希望计算的数的位数可达几十位甚至几百位，虽然计算机的计算精度也算较高了，但因受到硬件的限制，往往达不到实际问题所要求的精度。我们可以利用程序设计的方法去实现这样的高精度计算。计算结果超过常用的数据类型长度即可使用高精度计算。

int范围：[-2³¹,2³¹-1]，大约是10⁹数量级。long long范围[-2⁶³,2⁶³-1]，大约是10¹⁸数量级。超过这个量级，我们就可以选择高精度计算了。

---

一、高精度加法分析

1.1 数学的竖式加法计算

在进行高精度加法之前，我们来回顾一下小学时我们是如何进行加法计算的。我们以一个较小的数作为例子：计算12342+432的值。
我们很容易就能写出上面这个式子，计算的时候一会习惯性的从箭头位置从右往左进行计算得到结果。但是写到程序中还是这样吗？

1.2 数组模拟竖式计算

前面讲了，因为数据已经超过了常用的数据类型，存入过大的数据的时候是有问题的，所以我们在存储输入的数据的时候都是使用数组来完成，现在我们来看一下数组接受数据会发生什么情况。

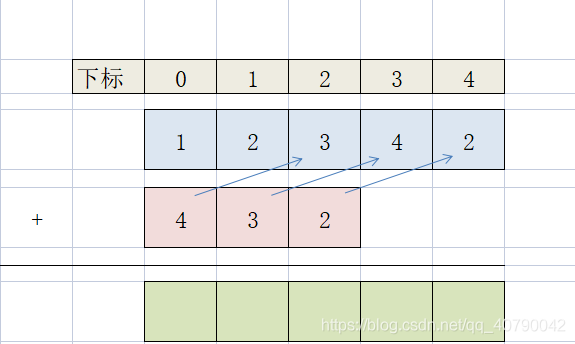
这里增加了下标，我们会发现一个问题，这时候想要计算，他们的下标不是对齐的，我们不能直接直接把0号下标的两个数直接相加。我们希望他们是尾部对齐的效果。那么解决这个问题我们可以先把这两个数组进行逆序(reverse)操作，算完之后再把结果倒序输出即可。顺便加上对应的数组。下图为逆序后做的计算。

1.3 计算步骤分析

根据上图，我们分析一下代码步骤。

1. 创建已知和未知的变量
2. 程序读取a数组和b数组，并将数组倒置（reverse）
3. 使用从左往右进行累加计算，并将结果存储到ans数组中。公式：ans[i]=a[i]+b[i];
4. 将结果逆序输出

二、使用步骤

2.1 代码结构

计算的位数我们设定为小于500位。在写代码的时候我们可以先把我们要做的流程利用函数的形式来表示，具体的实现，等我们想清楚之后再写，这样子写的时候思路更清晰，而且做什么事也不会写乱了。
代码如下（示例）：

#include 
#include 
using namespace std;
// 1. 创建变量(包括三个数组、数组的大小N、三个数组的长度,t表示进位)
const int N = 520;
int a[N],b[N],ans[N],len_a,len_b,len_ans,t;
void readDataAndReverse(int *arr,int &len);
void addData(int *a,int *b,int &len_ans);
void reversePrint(int *ans);
int main(){
	// 2. 读入数据并倒置
	readDataAndReverse(a,len_a);
	readDataAndReverse(b,len_b);
	// 3. 数组做累加
	addData(a,b,len_ans);
	// 4. 逆序输出
	reversePrint(ans);
	return 0;
}
void readDataAndReverse(int *arr,int &len){
	
}
void addData(int *a,int *b,int &len_ans){
	
}
void reversePrint(int *ans){
	
}

2.2 读入数据并倒置：readDataAndReverse(int *arr,int &len)函数

代码如下（示例）：

/*
函数功能:读入数据,并逆序存入数组
参数：
	arr：要存入数据的数组
	len：对应数组的长度
返回值：null
*/
void readDataAndReverse(int *arr,int &len){
	
	// 1. 由于数据量比较大,所以我们都是先读入字符串,再转存数组
	string s;
	cin>>s;
	len = s.length();		// 字符串的长度,就是对应数组(a,b数组)的长度
	/*
		i: 表示arr数组的下标,从1开始到len(不从零开始存,方便记忆)
		j: 表示s字符数组的下标,从结尾len开始到1
		s[j]-'0': s[j]得到的是一个字符数字,这个字符数字想要转成真正的数字需要减去0,详见ASCII码表
	*/
	for(int i=0,j=len-1;j>=0;i++,j--){
		arr[i] = s[j]-'0';
	}
}

测试：在两个输入的函数下面添加打印数组的代码做测试，是可以的。

2.3 两个数据相加：addData(int *a,int *b,int &len_ans)函数

这里我们增加一个变量t，t表示进位数值。我们思考这么一个问题，在前面的例子中，我们对两个数字进行累加的时候并没有考虑到a[i]+b[i]>=10的情况，如果不做进位维护的话，会导致结果和预期不一样。通过下图，我们再看一下程序改如何改进：

根据上面的图片，增加的部分是进位维护程序，并且是在得到ans数组之后进行的。

/*
函数功能:对两个数组进行累加
参数：
	a：a数组
	b：b数组
	len_ans：累加后的数组长度
返回值：null
*/
void addData(int *a,int *b,int &len_ans){
	// 1、得到a和b中最长的数组长度
	len_ans = len_a;
	if (len_a<len_b){
		len_ans = len_b;
	}
	// 做累加
	t=0;	// 进位，默认第一次累加为零
	for(int i=0;i<=len_ans;i++){
		ans[i] = a[i]+b[i]+t;
		t=0;	// 每次累加完之后归零，并不是每次都有进位
		// 进位维护，如果累加之后结果大于等于10，进位变1，结果%10
		if(ans[i]>=10){
			t = 1;
			ans[i]=ans[i]%10;
		}
	}
	// 累加完了之后判断最后进位t是否等于1，是的话说明还有一位数，我们手动加到数组中
	if(t==1){
		len_ans++;
		ans[len_ans-1]=1;
	}
}

输入数据做测试，需要自己在addData()后面添加打印程序。没有问题。

2.4 逆序输出：reversePrint(int *ans)函数

上一部分我们已经做了输出，发现并没有问题，到这一步，我们只是需要把它倒序输出吗？也就是下面的代码。
尝试输入：00123 00123
他会输出246吗？

void reversePrint(int *ans){
	for(int i=len_ans-1;i>0;i--){
		cout<<ans[i];
	} 
}

2.4.1 去除前导零

可以看到，并不是我们想要的结果，因为算出来的前面还有两个0，我们称这个为前导零。所以下面我们要做的就是去除前导零

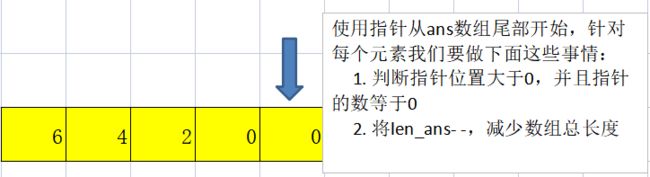
如何去除前导零呢？如上图所示，我们需要一个“指针”，当然这个并不是c++中的那个指针，这里只是表示指向那个位置的一个值，刚好这个值就是len_ans，所以用len_ans当这个“指针”就行。处理步骤按图上的来就行。

void reversePrint(int *ans){
	// 最后一个位置是len_ans-1，所以从ans[len_ans-1]开始判断
	while(ans[len_ans-1]==0&&len_ans-1>0){
		len_ans--;
	}
	// 逆序输出
	for(int i=len_ans-1;i>=0;i--){
		cout<<ans[i];
	} 
}

---

总结

高精度加法步骤：

1. 创建对应的数组变量及其他变量
2. 以字符串形式读入数据并逆序存储到数组中
3. 将两个数组做累加, 注意进位的维护
4. 逆序输出(注意删除前导零)

完整代码

1.使用函数形式

#include 
#include 
using namespace std;
// 1. 创建变量(包括三个数组、数组的大小N、三个数组的长度)
const int N = 520;
int a[N],b[N],ans[N],len_a,len_b,len_ans,t;
void readDataAndReverse(int *arr,int &len);
void addData(int *a,int *b,int &len);
void reversePrint();
int main(){
	// 2. 读入数据并倒置
	readDataAndReverse(a,len_a);
	readDataAndReverse(b,len_b);
	
	
	// 3. 数组做累加
	addData(a,b,len_ans);
	// 4. 逆序输出
	reversePrint();
	return 0;
}
void readDataAndReverse(int *arr,int &len){
	// 1. 由于数据量比较大,所以我们都是先读入字符串,再转存数组
	string s;
	cin>>s;
	len = s.length();		// 字符串的长度,就是对应数组(a,b数组)的长度
	/*
		i: 表示arr数组的下标,从1开始到len(不从零开始存,方便记忆)
		j: 表示s字符数组的下标,从结尾len开始到1
		s[j]-'0': s[j]得到的是一个字符数字,这个字符数字想要转成真正的数字需要减去0,详见ASCII码表
	*/
	for(int i=0,j=len-1;j>=0;i++,j--){
		arr[i] = s[j]-'0';
	}
}
void addData(int *a,int *b,int &len){
	// 1、得到a和b中最长的数组长度
	len_ans = len_a;
	if (len_a<len_b){
		len_ans = len_b;
	}
	// 做累加
	t=0;	// 进位，默认第一次累加为零
	for(int i=0;i<len_ans;i++){
		ans[i] = a[i]+b[i]+t;
		t=0;	// 每次累加完之后归零，并不是每次都有进位
		// 进位维护，如果累加之后结果大于等于10，进位变1，结果%10
		if(ans[i]>=10){
			t = 1;
			ans[i]=ans[i]%10;
		}
	}
	// 累加完了之后判断最后进位t是否等于1，是的话说明还有一位数，我们手动加到数组中
	if(t==1){
		len_ans++;
		ans[len_ans-1]=1;
	}
}
void reversePrint(){
	// 最后一个位置是len_ans-1，所以从ans[len_ans-1]开始判断
	while(ans[len_ans-1]==0&&len_ans-1>0){
		len_ans--;
	}
	// 逆序输出
	for(int i=len_ans-1;i>=0;i--){
		cout<<ans[i];
	} 
}

2.不使用函数形式

#include 
#include 
using namespace std;
// 1. 创建变量(包括三个数组、数组的大小N、三个数组的长度)
const int N = 520;
int a[N],b[N],ans[N],len_a,len_b,len_ans,t;
int main(){
	// 2. 读入数据并倒置
	string s;
	cin>>s;
	len_a = s.length();		
	for(int i=0,j=len_a-1;j>=0;i++,j--){
		a[i] = s[j]-'0';
	}
	cin>>s;
	len_b = s.length();		
	for(int i=0,j=len_b-1;j>=0;i++,j--){
		b[i] = s[j]-'0';
	}
	
	// 1、得到a和b中最长的数组长度
	len_ans = len_a;
	if (len_a<len_b){
		len_ans = len_b;
	}
	// 做累加
	t=0;	// 进位，默认第一次累加为零
	for(int i=0;i<len_ans;i++){
		ans[i] = a[i]+b[i]+t;
		t=0;	// 每次累加完之后归零，并不是每次都有进位
		// 进位维护，如果累加之后结果大于等于10，进位变1，结果%10
		if(ans[i]>=10){
			t = 1;
			ans[i]=ans[i]%10;
		}
	}
	// 累加完了之后判断最后进位t是否等于1，是的话说明还有一位数，我们手动加到数组中
	if(t==1){
		len_ans++;
		ans[len_ans-1]=1;
	}
	
	// 最后一个位置是len_ans-1，所以从len_ans-1开始判断
	while(ans[len_ans-1]==0&&len_ans-1>0){
		len_ans--;
	}
	// 逆序输出
	for(int i=len_ans-1;i>=0;i--){
		cout<<ans[i];
	} 
	
	return 0;
}

优化

程序代码还可以在进行优化，例如数组倒置，或者是求取len_a和len_b中的最大值，都可以使用algorithm头文件进行处理，这里就自行查阅数据学习了。

初次学习，写的不足或者看不懂的地方请留言。