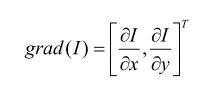opencv实战4-图像滤波
一、图像滤波基础
滤波器作为图像处理课程的重要内容,大致可分为两类,空域滤波器和频率域滤波器。
常见的线性滤波有:均值滤波、高斯滤波、盒子滤波、拉普拉斯滤波等,通常线性滤波器之间只是模版系数不同。
非线性滤波利用原始图像跟模版之间的一种逻辑关系得到结果,如最值滤波器,中值滤波器和双边滤波器等。
卷积:
我们有一个二维的滤波器矩阵(有个高大上的名字叫卷积核)和一个要处理的二维图像。然后,对于图像的每一个像素点,计算它的邻域像素和滤波器矩阵的对应元素的乘积,然后加起来,作为该像素位置的值。这样就完成了滤波过程。
对图像和滤波矩阵进行逐个元素相乘再求和的操作就相当于将一个二维的函数移动到另一个二维函数的所有位置,这个操作就叫卷积或者协相关。卷积和协相关的差别是,卷积需要先对滤波矩阵进行180的翻转。
二、空域滤波
2.1 均值滤波
将每个像素的值替换为该像素领域内平均值。
cv::blur(image,result, cv::Size(5,5)); // 滤波器尺寸2.2 高斯滤波
2.2.1 高斯滤波简介
有时需要让邻域内较近的像素具有更高的重要度。因此可计算加权平均值,即较近的像素比
较远的像素具有更大的权重。要得到加权平均值,可采用依据高斯函数(即“钟形曲线”函数)
制定的加权策略。
高斯滤波器是一种线性滤波器,能够有效的抑制噪声,平滑图像。
高斯滤波后图像被平滑的程度取决于标准差。它的输出是领域像素的加权平均,同时离中心越近的像素权重越高。因此,相对于均值滤波(mean filter)它的平滑效果更柔和,而且边缘保留的也更好。
2.2.2 高斯滤波步骤
高斯滤波的具体操作是:用一个模板(或称卷积、掩模)扫描图像中的每一个像素,用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。
2.2.3 高斯滤波特性
高斯函数具有五个重要的性质:
(1)二维高斯函数具有旋转对称性,即滤波器在各个方向上的平滑程度是相同的.一般来说,一幅图像的边缘方向是事先不知道的,因此,在滤波前是无法确定一个方向上比另一方向上需要更多的平滑.旋转对称性意味着高斯平滑滤波器在后续边缘检测中不会偏向任一方向.
(2)高斯函数是单值函数.这表明,高斯滤波器用像素邻域的加权均值来代替该点的像素值,而每一邻域像素点权值是随该点与中心点的距离单调增减的.这一性质是很重要的,因为边缘是一种图像局部特征,如果平滑运算对离算子中心很远的像素点仍然有很大作用,则平滑运算会使图像失真.
(3)高斯函数的傅立叶变换频谱是单瓣的.正如下面所示,这一性质是高斯函数付立叶变换等于高斯函数本身这一事实的直接推论.图像常被不希望的高频信号所污染(噪声和细纹理).而所希望的图像特征(如边缘),既含有低频分量,又含有高频分量.高斯函数付立叶变换的单瓣意味着平滑图像不会被不需要的高频信号所污染,同时保留了大部分所需信号.
(4)高斯滤波器宽度(决定着平滑程度)是由参数σ表征的,而且σ和平滑程度的关系是非常简单的.σ越大,高斯滤波器的频带就越宽,平滑程度就越好.通过调节平滑程度参数σ,可在图像特征过分模糊(过平滑)与平滑图像中由于噪声和细纹理所引起的过多的不希望突变量(欠平滑)之间取得折衷.
(5)由于高斯函数的可分离性,较大尺寸的高斯滤波器可以得以有效地实现.二维高斯函数卷积可以分两步来进行,首先将图像与一维高斯函数进行卷积,然后将卷积结果与方向垂直的相同一维高斯函数卷积.因此,二维高斯滤波的计算量随滤波模板宽度成线性增长而不是成平方增长。
2.2.4 高斯滤波原理
高斯滤波使用的高斯核为x和y两个一维高斯的乘积,两个维度上的标准差σ通常相同,形式如下:![]()
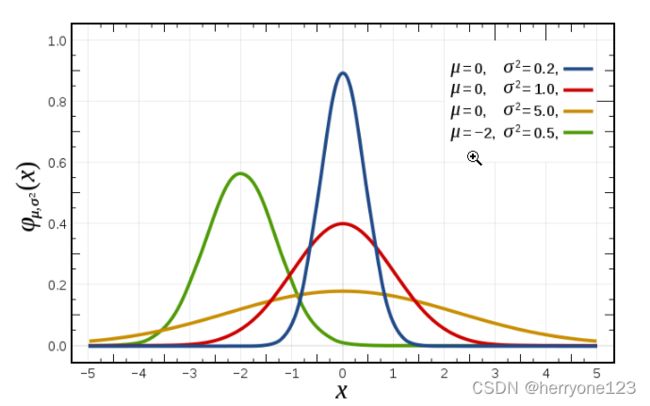
高斯核可以看成是与中心距离负相关的权重。平滑时,调整σ实际是在调整周围像素对当前像素的影响程度,调大σ即提高了远处像素对中心像素的影响程度,滤波结果也就越平滑。高斯曲线随σ变化的曲线如下:
2.2.5 opencv高斯滤波实现
在 OpenCV 中,若要对图像应用高斯滤波器,需要调用函数 cv::GaussianBlur ,并且提供系数的个数(第三个参数,必须是奇数)和 σ 的值(第四个参数)。也可以只设置 σ 的值,由OpenCV决定系数的个数(输入滤波器尺寸的值为 0 )。反过来也可以,即输入参数时提供尺寸的数值,σ值为 0 。函数会自行判断最适合尺寸的 σ值。
cv::GaussianBlur(image, result,
cv::Size(5,5), // 滤波器尺寸
1.5); // 控制高斯曲线形状的参数2.3 中值滤波
中值滤波(Median Filter)是一种典型的非线性滤波技术,基本思想是用像素点领域灰度值的中值来代替像素点的灰度值,该方法在去除脉冲噪声,椒盐噪声的同时又能保留图像边缘信息;
中值滤波是基于排序统计理论的一种能够有效地抑制噪声的非线性信号处理技术,其基本原理是把数字图像或数字序列中一点的值用该点的一个领域内各点值的中值代替,让周围的像素值接近真实值,从而消除孤立的噪声点,对于斑点噪声(Speckle noise)和椒盐噪声(salt-pepper noise)来说尤其有用,因为它不依赖于领域内那些与典型值差别很大的值;
计算过程:
- 获取目标像素值周围一定领域范围的像素值;
- 按灰度值进行从小到大的排序
- 选择排序后的中间值作为,替代掉目标像素值;
中值滤波器对消除椒盐噪声非常有用。中值滤波器把当前像素和它的邻域组成一个集合,然后计算出这个集合的中间值,以此作为当前像素的值(集合中数值经过排序,中间位置的数值就是中间值)。当前像素被中间值代替。
cv::medianBlur(image, result, 5); OpenCV中medianBlur API的介绍如下:
void medianBlur( InputArray src, OutputArray dst, int ksize );
src需要滤波的原图像dst中值滤波后输出图像ksize表示领域范围大小,必须是一个奇数;
// 创建结果存放位置
cv::Mat result;
// 设置中值滤波窗大小
const int winSize = 21;
// 中值滤波
cv::medianBlur(origin, result, winSize);2.4 定向滤波器检测边缘
2.4.1 Sobel
Sobel 算子是一种典型的用于边缘检测的线性滤波器,它基于两个简单的 3×3 内核。
如果把图像看作二维函数,那么 Sobel 算子就是图像在垂直和水平方向变化的速度。在数
学术语中,这种速度称为梯度。它是一个二维向量,向量的元素是横竖两个方向的函数的一
阶导数:
Sobel 算子在水平和垂直方向计算像素值的差分,得到图像梯度的近似值。它在像素周围的
一定范围内进行运算,以减少噪声带来的影响。
cv::Sobel(image, // 输入
sobel, // 输出
image_depth, // 图像类型
xorder,yorder, // 内核规格
kernel_size, // 正方形内核的尺寸
alpha, beta); // 比例和偏移量2.5 拉普拉斯算子
拉普拉斯算子也是一种基于图像导数运算的高通线性滤波器,它通过计算二阶导数来度量图
像函数的曲率。
参考文献:
【1】图像滤波之高斯滤波介绍 :图像滤波之高斯滤波介绍 - 淇淇宝贝 - 博客园
【2】图像处理之高斯滤波: 图像处理之高斯滤波_程序员深度学习-CSDN博客_图像处理高斯滤波
【3】 数字图像处理之高斯滤波:数字图像处理之高斯滤波_shandianfengfan的博客-CSDN博客
【4】OpenCv学习篇——图像高斯滤波算法: OpenCv学习篇——图像高斯滤波算法_fzhykx的博客-CSDN博客_高斯滤波算法
【5】线性滤波和卷积的概念 ,线性和非线性对比理解: 线性滤波和卷积的概念 ,线性和非线性对比理解_陆::zw的博客-CSDN博客_什么是线性滤波