【机器学习】01. 波士顿房价为例子学习线性回归(代码注释,思路推导)
目录
-
- 资源下载
- 0.数据处理
- 1. 可导线性回归解法
- 2. 梯度下降解法
- 3. 随机梯度下降
- 总结
『机器学习』分享机器学习课程学习笔记,逐步讲述从简单的线性回归、逻辑回归到 ▪ 决策树算法 ▪ 朴素贝叶斯算法 ▪ 支持向量机算法 ▪ 随机森林算法 ▪ 人工神经网络算法 等算法的内容。
欢迎关注 『机器学习』 系列,持续更新中
欢迎关注 『机器学习』 系列,持续更新中
资源下载
拿来即用,所见即所得。
项目仓库:https://gitee.com/miao-zehao/machine-learning/tree/master
0.数据处理
- 使用pd读取数据,使用
.values转为np数组,当然你也可以直接用np读取,看个人喜好。
datafile = 'boston.csv'
data = pd.read_csv(datafile) #
feature_names = list(data.columns) # 获取列名
data = data.values # .values转为np数组
- 正常流程还需要对于数组进行维度处理(本次数据集不需要处理)
- 数据归一化
# 计算训练集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
- 划分训练集和测试集,各占80%和20%
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]#得到分割的训练集 80%
- 封装成载入数据的函数,以备后面调用
def load_data():
import pandas as pd
def load_data():
# 从文件导入数据
datafile = 'boston.csv'
data = pd.read_csv(datafile) #
feature_names = list(data.columns) # 获取列名
data = data.values # .values转为np数组
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]#得到分割的训练集 80%
# 计算训练集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
training_data, test_data=load_data()
#这里其实我不需要导出dat文件,我一般比较喜欢用csv,可能大数据量的话,dat文件会好一点吧
#在网上是在是找不到相关的python使用dat文件做模型的学习资源,也不知道这样转对不对
pd.DataFrame(training_data,index=None,columns=None).to_csv('training_data.dat')
pd.DataFrame(test_data).to_csv('test_data.dat')
1. 可导线性回归解法
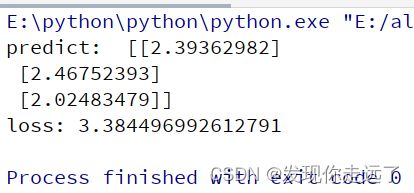
这里只是简单的计算多个样本的预测值和损失函数,并且调用了我们前面封装好的读取数据函数。
import numpy as np
import pandas as pd
def load_data():
# 从文件导入数据
datafile = 'boston.csv'
data = pd.read_csv(datafile) #
feature_names = list(data.columns) # 获取列名
data = data.values # .values转为np数组
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]#得到分割的训练集 80%
# 计算训练集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
# 获取数据
training_data, test_data = load_data()
x = training_data[:, :-1]
y = training_data[:, -1:]
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost
net = Network(13)
# 此处可以一次性计算多个样本的预测值和损失函数
x1 = x[0:3]
y1 = y[0:3]
z = net.forward(x1)
print('predict: ', z)
loss = net.loss(z, y1)
print('loss:', loss)
2. 梯度下降解法
代码量看起来比较繁多,其实是因为有一个推导思路的过程,有1个梯度演示图绘制和2个network网络函数,先用一个2个参数变量的梯度图说明了梯度下降的原理,再用2个参数的梯度下降训练绘图,再用13个参数的梯度下降训练绘图。
np.save('2.梯度下降模型权重文件.npy', net.w)
np.save('2.梯度下降模型非线性文件.npy', net.b)
import numpy as np
import pandas as pd
############################数据读入############################
def load_data():
# 从文件导入数据
datafile = 'boston.csv'
data = pd.read_csv(datafile) #
feature_names = list(data.columns) # 获取列名
data = data.values # .values转为np数组
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]#得到分割的训练集 80%
# 计算训练集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
training_data, test_data = load_data()
x = training_data[:, :-1]
y = training_data[:, -1:]
############################梯度图展示绘制############################
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost
net = Network(13)
losses = []
#只画出参数w5和w9在区间[-160, 160]的曲线部分,以及包含损失函数的极值
w5 = np.arange(-160.0, 160.0, 1.0)
w9 = np.arange(-160.0, 160.0, 1.0)
losses = np.zeros([len(w5), len(w9)])
#计算设定区域内每个参数取值所对应的Loss
for i in range(len(w5)):
for j in range(len(w9)):
net.w[5] = w5[i]
net.w[9] = w9[j]
z = net.forward(x)
loss = net.loss(z, y)
losses[i, j] = loss
#使用matplotlib将两个变量和对应的Loss作3D图
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
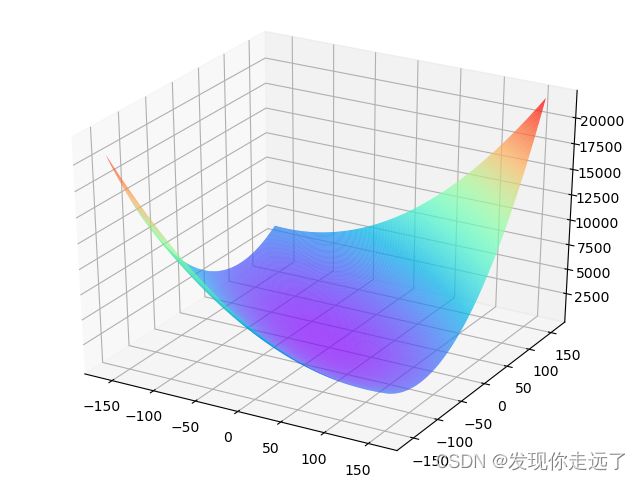
#如何选择[w5′,w9′]是至关重要的,
# 第一要保证LLL是下降的,
# 第二要使得下降的趋势尽可能的快。
# 微积分的基础知识告诉我们:沿着梯度的反方向,是函数值下降最快的方向(越快增长也意味着我们反向x轴看时是越快下降
# 函数在某一个点的梯度方向是曲线斜率最大的方向,但梯度方向是向上的,所以下降最快的是梯度的反方向
w5, w9 = np.meshgrid(w5, w9)
ax.plot_surface(w5, w9, losses, rstride=1, cstride=1, cmap='rainbow')
plt.savefig("双参数的一张梯度演示图.png")
plt.show()#绘制一张梯度演示图
############################只有w5和w9的梯度下降############################
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.w[5] = -100.
self.w[9] = -100.
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z - y) * x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b
def update(self, gradient_w5, gradient_w9, eta=0.01):
net.w[5] = net.w[5] - eta * gradient_w5
net.w[9] = net.w[9] - eta * gradient_w9
def train(self, x, y, iterations=100, eta=0.01):
points = []
losses = []
for i in range(iterations):
points.append([net.w[5][0], net.w[9][0]])
z = self.forward(x)
L = self.loss(z, y)
gradient_w, gradient_b = self.gradient(x, y)
gradient_w5 = gradient_w[5][0]
gradient_w9 = gradient_w[9][0]
self.update(gradient_w5, gradient_w9, eta)
losses.append(L)
if i % 50 == 0:
print('iter {}, point {}, loss {}'.format(i, [net.w[5][0], net.w[9][0]], L))
return points, losses
# 获取数据
train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
# 创建网络
net = Network(13)
num_iterations = 2000
# 启动训练
points, losses = net.train(x, y, iterations=num_iterations, eta=0.01)
# 画出损失函数的变化趋势
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()
############################13个全部参数的梯度下降############################
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z - y) * x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta=0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, x, y, iterations=100, eta=0.01):
losses = []
for i in range(iterations):
z = self.forward(x)
L = self.loss(z, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(L)
if (i + 1) % 10 == 0:
print('iter {}, loss {}'.format(i, L))
return losses
# 获取数据
train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
# 创建网络
net = Network(13)
num_iterations = 1000
# 启动训练
losses = net.train(x, y, iterations=num_iterations, eta=0.01)
# 画出损失函数的变化趋势
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.savefig("2.梯度下降解法图.png")
plt.show()
#Numpy提供了save接口,可直接将模型权重数组保存为.npy格式的文件。
np.save('2.梯度下降模型权重文件.npy', net.w)
np.save('2.梯度下降模型非线性文件.npy', net.b)
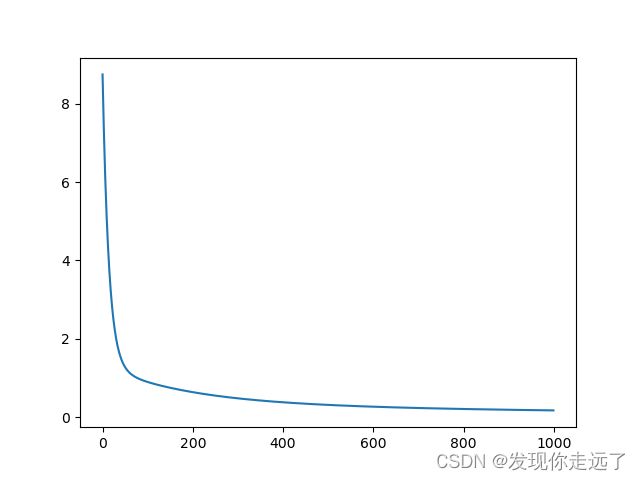
输出内容显示我们的损失一直在减小,先快后慢。
iter 9, loss 5.14339432579551
iter 19, loss 3.097924194225988
iter 29, loss 2.0822410206170265
iter 39, loss 1.5673801618157397
iter 49, loss 1.296620473507743
······省略
iter 919, loss 0.18777618462820617
iter 929, loss 0.18608798277314587
iter 939, loss 0.18443254350353397
iter 949, loss 0.1828087743610396
iter 959, loss 0.18121563232764157
iter 969, loss 0.1796521213045923
iter 979, loss 0.17811728972507232
iter 989, loss 0.17661022829336182
iter 999, loss 0.17513006784373503
3. 随机梯度下降
随机梯度下降相比较梯度下降来说核心在于每次不要对全局数据求解梯度下架,而是取局部的数据,因为很多时候局部的特征就够用了(在数据比较多的时候)以此来快速操作。
import numpy as np
import pandas as pd
############################数据读入############################
from matplotlib import pyplot as plt
def load_data():
# 从文件导入数据
datafile = 'boston.csv'
data = pd.read_csv(datafile) #
feature_names = list(data.columns) # 获取列名
data = data.values # .values转为np数组
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]#得到分割的训练集 80%
# 计算训练集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
import numpy as np
class Network(object):
def __init__(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
# np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
N = x.shape[0]
gradient_w = 1. / N * np.sum((z - y) * x, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = 1. / N * np.sum(z - y)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta=0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, training_data, num_epochs, batch_size=10, eta=0.01):
n = len(training_data)
losses = []
for epoch_id in range(num_epochs):
# 在每轮迭代开始之前,将训练数据的顺序随机打乱
# 然后再按每次取batch_size条数据的方式取出
np.random.shuffle(training_data)
# 将训练数据进行拆分,每个mini_batch包含batch_size条的数据
mini_batches = [training_data[k:k + batch_size] for k in range(0, n, batch_size)]
for iter_id, mini_batch in enumerate(mini_batches):
# print(self.w.shape)
# print(self.b)
x = mini_batch[:, :-1]
y = mini_batch[:, -1:]
a = self.forward(x)
loss = self.loss(a, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(loss)
print('Epoch {:3d} / iter {:3d}, loss = {:.4f}'.
format(epoch_id, iter_id, loss))
return losses
# 获取数据
train_data, test_data = load_data()
# 创建网络
net = Network(13)
# 启动训练
losses = net.train(train_data, num_epochs=50, batch_size=100, eta=0.1)
# 画出损失函数的变化趋势
plot_x = np.arange(len(losses))
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.savefig("3.随机梯度下降解法图.png")
plt.show()
#Numpy提供了save接口,可直接将模型权重数组保存为.npy格式的文件。
np.save('3.随机梯度下降模型权重文件.npy', net.w)
np.save('3.随机梯度下降模型非线性文件.npy', net.b)
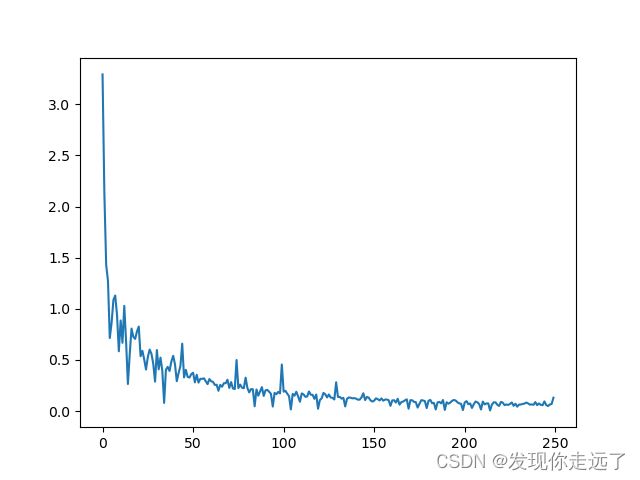
输出内容,很明显可以看到我们的损失呈现出来回波动,但是一直总体趋向于变小
Epoch 0 / iter 0, loss = 30.5122
Epoch 0 / iter 1, loss = 12.7252
Epoch 0 / iter 2, loss = 6.5755
Epoch 0 / iter 3, loss = 2.8248
-------------省略---------------
Epoch 49 / iter 1, loss = 0.0547
Epoch 49 / iter 2, loss = 0.0497
Epoch 49 / iter 3, loss = 0.0795
Epoch 49 / iter 4, loss = 0.0287
## 4. 不同学习力的梯度下降 与前面第三部分有所不同的是,我们这里把学习力也设置为一个参数,使用for循环多次训练并绘制在同一张图片中,研究学习力对于损失的影响。 
import numpy as np
import pandas as pd
############################数据读入############################
from matplotlib import pyplot as plt
def load_data():
# 从文件导入数据
datafile = 'boston.csv'
data = pd.read_csv(datafile) #
feature_names = list(data.columns) # 获取列名
data = data.values # .values转为np数组
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]#得到分割的训练集 80%
# 计算训练集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
training_data, test_data = load_data()
x = training_data[:, :-1]
y = training_data[:, -1:]
############################13个全部参数的梯度下降############################
#因为要涉及不同学习力的影响,所以我们修改一下网络函数,新增参数eta
class Network(object):
def __init__(self, num_of_weights,eta):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z - y) * x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b,eta):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, x, y, eta,iterations=100):
losses = []
for i in range(iterations):
z = self.forward(x)
L = self.loss(z, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b,eta)
losses.append(L)
if (i + 1) % 10 == 0:
print('iter {}, loss {}'.format(i, L))
return losses
# 获取数据
train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
# 创建网络
for i in [j/100 for j in range(1,10)]:
net = Network(13,eta=i)
num_iterations = 1000
# 启动训练
losses = net.train(x, y, iterations=num_iterations,eta=i)
# 画出损失函数的变化趋势
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.legend([j/100 for j in range(1,10)], fontsize=18, edgecolor="black", loc='lower right', frameon=True)
plt.savefig("4.不同学习力的梯度下降图.png")
plt.show()

根据图片可以清晰的看到,学习力越小,那么损失下降的幅度就越小,但是这会带来计算量的增加,而且学习力过大,虽然可以减少计算,但也可能会跳过最低点,导致偏离理想最低点过多。
总结
大家喜欢的话,给个,点个关注!给大家分享更多有趣好玩的python机器学习知识!
参考的学习资料:百度飞浆机器学习平台
欢迎关注 『机器学习』 系列,持续更新中
欢迎关注 『机器学习』 系列,持续更新中
【机器学习】01. 波士顿房价为例子学习线性回归
【机器学习】02. 使用sklearn库牛顿化、正则化的逻辑回归
【机器学习】03. 支持向量机SVM库进行可视化分类
【更多内容敬请期待】