一文掌握爱因斯坦求和约定 einsum
爱因斯坦跟 NumPy 有关系吗?没有,但他提出了一个针对数学公式的符号简化办法,即爱因斯坦求和约定(Einstein Summation Convention)或者叫爱因斯坦标记法(Einstein Notation)。
他这套方法不仅方便了相关理论的书写,而且意外地给如今数据科学中编程实现相关计算带来了方便,让我们来看看到底怎么回事。
引言
先瞄一眼爱因斯坦当年在论文广义相对论的基础里涉及的一些数学公式。
看着比较繁琐吧,如果学过微分几何的应该熟悉这套的。意大利数学家雷戈里奥·里奇(Gregorio Ricci-Curbastro)在研究黎曼、克里斯托费尔等人的黎曼几何微分不变量时提出了绝对微分学,然后与他学生勒维·季维塔(Levi-Givita)创立了张量分析。而黎曼几何和张量分析正是爱因斯坦广义相对论的数学基础。
要注意的是,张量分析中的张量指一种特殊的多重线性映射,在相关基底给定的情况下可以用一个多维数组表示,而 NumPy 和 PyTorch 等软件包中的张量特指多维数组。
在张量分析中,为了分别处理张量随坐标变换的协变和逆变,引入了上下标,上标表示逆变张量的分量,下标表示协变张量的分量,它们根据基底的变化分别进行逆变或协变。
g m n Γ m β σ Γ n μ β − g v σ Γ μ β a Γ ν a β g^{m n} \Gamma_{m \beta}^{\sigma} \Gamma_{n \mu}^{\beta}-g^{v \sigma} \Gamma_{\mu \beta}^{a} \Gamma_{\nu a}^{\beta} gmnΓmβσΓnμβ−gvσΓμβaΓνaβ
通常,当处理协变张量和逆变张量时,其中上下标的位置也指示了张量类型以及缩并方式。
但是,爱因斯坦求和约定也可以有不同应用方式。例如,更一般的情况是坐标基底固定,或者不考虑坐标的情况时,则可以选择仅使用下标。在 NumPy 或 PyTorch 等程序中涉及的更多情况就是这个样子。
像向量内积,矩阵-向量乘法,以及矩阵乘法都可以用这套标记法来简化书写。
例如向量内积,
v i ∂ ∂ x i = v 1 ∂ ∂ x 1 + v 2 ∂ ∂ x 2 + v 3 ∂ ∂ x 3 v^{i} \frac{\partial}{\partial x^{i}} =v^{1} \frac{\partial}{\partial x^{1}}+v^{2} \frac{\partial}{\partial x^{2}}+v^{3} \frac{\partial}{\partial x^{3}} vi∂xi∂=v1∂x1∂+v2∂x2∂+v3∂x3∂
矩阵 A i j A_{i j} Aij 乘以向量 v j v_{j} vj,
u i = ( A v ) i = ∑ j = 1 N A i j v j \mathbf{u}_{i}=(\mathbf{A} \mathbf{v})_{i}=\sum_{j=1}^{N} A_{i j} v_{j} ui=(Av)i=j=1∑NAijvj
可以记为,
u i = A j i v j 或者 u i = A i j v j u^{i}=A_{\;j}^{i} v^{j} \;\text{ 或者 }\; u_{i}=A_{ij} v_{j} ui=Ajivj 或者 ui=Aijvj
而矩阵 A i j A_{i j} Aij 和 B j k B_{j k} Bjk 相乘,
C i k = ( A B ) i k = ∑ j = 1 N A i j B j k \mathbf{C}_{i k}=(\mathbf{A} \mathbf{B})_{i k}=\sum_{j=1}^{N} A_{i j} B_{j k} Cik=(AB)ik=j=1∑NAijBjk
可以记为,
C k i = A j i B k j 或者 C i k = A i j B j k C_{\;k}^{i}=A_{\;j}^{i} B_{\;k}^{j} \;\text{ 或者 }\; C_{ik}=A_{ij} B_{jk} Cki=AjiBkj 或者 Cik=AijBjk
NumPy 之 einsum
本文主要介绍 NumPy 中实现的爱因斯坦求和约定,而像 PyTorch、TensorFlow 等情况基本类似。
这里主要拿来处理高维数组的相关计算,并不需要上下标那一套,而是统一针对下标来简化求和连加符。使用时需要明确的是下面这几点,
- 哪几个输入数组参与运算
- 沿输入的哪些轴(维度)计算乘积
- 输出数组需要保留哪些轴
具体反映在函数 np.einsum 的参数上,比如下图所示的例子,三个颜色对应三个输入张量,分别是 2 维数组,3 维数组和 2 维数组,而输出张量是 2 维数组。
看个例子
为了快速了解 einsum,我们直接来看一个向量乘以矩阵的例子。
import numpy as np
A = np.array([0,1,2])
A
array([0, 1, 2])
B = np.arange(12).reshape(3, 4)
B
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
将 A 看成行向量,然后乘以(矩阵乘法)B,得到一个 1x4 的向量。
# 这样吗?
A*B
我们知道,NumPy 这里的运算是元素级别的运算,因此是通过广播机制将 A 扩展为与 B 同样大小的二维数组。但是,很可惜,此处 A 的 shape 为 (3),而 B 的 shape 为 (3,4),它们并不符合广播的条件,因此出错。
ValueError: operands could not be broadcast together with shapes (3,) (3,4)
增加一个新轴,让 A 的 shape 变成 (3,1),然后就可以广播了。如果不知道 NumPy 的广播机制,可以出门看另一篇。
C = A[:, np.newaxis]*B
C比如下图所示的例子,三个颜色对应三个输入张量,分别是 `2` 维数组,`3` 维数组和 `2` 维数组,而输出张量是 `2` 维数组。
array([[ 0, 0, 0, 0],
[ 4, 5, 6, 7],
[16, 18, 20, 22]])
然后将每一列的数字加起来,得到一个有 4 个元素的向量。
C.sum(axis=0)
array([20, 23, 26, 29])
# 组合在一起
(A[:, np.newaxis]* B).sum(axis=0)
array([20, 23, 26, 29])
使用爱因斯坦求和约定来实现,将变得更加简洁高效。
D = np.einsum('i,ij->j', A, B)
D
array([20, 23, 26, 29])
字符串 'i,ij->j' 由 '->' 分成了两部分,它左边的 'i,ij' 对应两个输入,而右边的 'j' 对应输出。输出中没有下标 'i',说明对两个输入沿着这个下标求和,而 j 所在的轴仍然保留。而 j 下标有 0 到 3 共 4 个值,因此最终得到一个有 4 个元素的向量。对应如下公式,
∑ i A i B i j \sum_i A_i B_{ij} i∑AiBij
对比一下效率,
%timeit (A[:, np.newaxis]* B).sum(axis=0)
3.46 µs ± 429 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
%timeit np.einsum('i,ij->j', A, B)
1.18 µs ± 34.1 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
当然,这个简单例子我们自然可以用内积 dot 来计算。这也是为数不多的效率比爱因斯坦求和约定更高的情况,而大多数情况下,爱因斯坦求和约定效率更高。
%timeit A.dot(B)
655 ns ± 12.5 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
# 或者
np.dot(B.T,A)
array([20, 23, 26, 29])
但是,einsum 可以很方便地实现如下计算,
E = np.einsum('i,ij->i', A, B)
E
array([ 0, 22, 76])
此时,输出中没有下标 'j',说明对两个输入沿着这个下标求和,而 i 所在的轴仍然保留。而 i 下标有 0 到 2 共 3 个值,因此最终得到一个有 3 个元素的向量。对应如下公式,
∑ j A i B i j . \sum_j A_i B_{ij}. j∑AiBij.
注意,连加符里的下标会消失,但没有出现在连加符里的下标以及相应的轴会保留。
使用说明
一般来说,使用 einsum 时是为了对输入的一些数组沿着某些轴作乘积运算,那对这些轴当然有一定要求,比如沿着相同标号的轴的元素个数一样多。
具体操作时,不妨先写出你要计算的数学公式,然后把连加符去掉,再根据输入输出的下标确定 einsum 中的参数。
下图给出一个例子,先写出计算公式,再转化为 np.einsum 里的字符串。
关键是为输入数组的轴和我们想要输出的数组选择正确的标签。可以选择两种方式之一执行此操作,使用字符串或者使用整数列表。这里使用前者,即使用字符串来表达数学公式。
一个很好的例子是矩阵乘法,它将行与列相乘,然后对乘积结果求和。
- 对于两个二维数组
A和B,矩阵乘法操作可以用np.einsum('ij,jk->ik', A, B)完成。 - 字符串
'ij,jk->ik'是什么意思? - 它被箭头
->分成两部分。左侧部分标记输入数组的轴:'ij'标记A以及'jk'标记B。字符串的右侧部分用字母'ik'标记单个输出数组的轴。 - 即输入两个二维数组,输出一个新的二维数组。
A = np.array([[1,1,1],
[2,2,2],
[5,5,5]])
B = np.array([[0,1,0],
[1,1,0],
[1,1,1]])
np.einsum('ij,jk->ik', A, B)
array([[ 2, 3, 1],
[ 4, 6, 2],
[10, 15, 5]])
看下图,注意轴的颜色,j 所在的轴被缩并掉了。
真相,‘ij,jk->ik’ 背后对应的数学公式
∑ j A i j B j k \large\sum_{j} A_{ij} B_{jk} j∑AijBjk
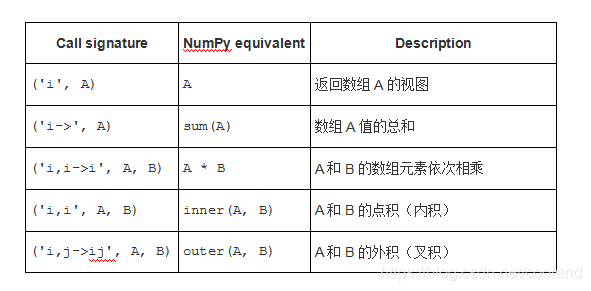
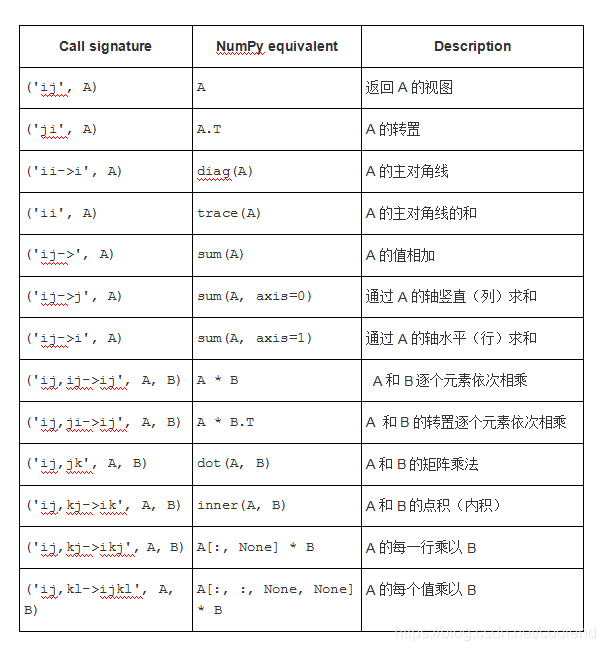
np.einsum 可以替代如下常用的运算,
- 矩阵求迹:
trace - 求矩阵对角线:
diag - 张量(沿轴)求和:
sum - 张量转置:
transopose - 矩阵乘法:
dot - 张量乘法:
tensordot - 向量内积:
inner - 外积:
outer
a = np.array([1,1,1])
b = np.array([2,3,4])
%%timeit
np.inner(a, b)
765 ns ± 13.2 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
%%timeit
np.einsum('i,i->', a, b)
1.06 µs ± 2.13 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
%%time
np.outer(a,b)
CPU times: user 44 µs, sys: 0 ns, total: 44 µs
Wall time: 46.7 µs
array([[2, 3, 4],
[2, 3, 4],
[2, 3, 4]])
# 用 einsum 计算外积
np.einsum('i,j->ij',a,b)
array([[2, 3, 4],
[2, 3, 4],
[2, 3, 4]])
%%timeit
np.einsum('i,j->ij',a,b)
1.18 µs ± 2.12 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
求迹
a = np.arange(9).reshape((3,3))
a
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
np.trace(a)
12
np.einsum('ii->',a)
12
# 或者
np.einsum('ii',a)
12
矩阵乘法 dot
# 1d
a = np.array([1,1,1])
b = np.array([2,3,4])
%%time
# dot
a.dot(b)
CPU times: user 20 µs, sys: 0 ns, total: 20 µs
Wall time: 23.4 µs
9
%%time
np.einsum('i,i->', a,b)
CPU times: user 47 µs, sys: 1 µs, total: 48 µs
Wall time: 53.4 µs
9
# 2d
a = np.arange(20).reshape(4,5)
b = np.arange(15).reshape(5,3)
%%time
# dot
a.dot(b)
CPU times: user 33 µs, sys: 0 ns, total: 33 µs
Wall time: 38.6 µs
array([[ 90, 100, 110],
[240, 275, 310],
[390, 450, 510],
[540, 625, 710]])
%%time
a@b
CPU times: user 48 µs, sys: 1e+03 ns, total: 49 µs
Wall time: 53.9 µs
array([[ 90, 100, 110],
[240, 275, 310],
[390, 450, 510],
[540, 625, 710]])
%%time
np.einsum('ij,jk->ik', a,b)
CPU times: user 30 µs, sys: 0 ns, total: 30 µs
Wall time: 32.4 µs
array([[ 90, 100, 110],
[240, 275, 310],
[390, 450, 510],
[540, 625, 710]])
张量 dot
- 方法
np.tensordot是沿着轴指定的子数组做点乘操作,即沿着axes指出的轴求和,最终这些轴就消失了。从这个例子可以看出,这个方法虽然使用方便,但效率远不如上面几个。
%%time
np.tensordot(a, b, axes=([1,],[0,]))
CPU times: user 209 µs, sys: 4 µs, total: 213 µs
Wall time: 211 µs
array([[ 90, 100, 110],
[240, 275, 310],
[390, 450, 510],
[540, 625, 710]])
思考,‘ij,jk->ijk’ 是什么操作?
r = np.einsum('ij,jk->ijk', a, b)
r
array([[[ 0, 0, 0],
[ 3, 4, 5],
[ 12, 14, 16],
[ 27, 30, 33],
[ 48, 52, 56]],
[[ 0, 5, 10],
[ 18, 24, 30],
[ 42, 49, 56],
[ 72, 80, 88],
[108, 117, 126]],
[[ 0, 10, 20],
[ 33, 44, 55],
[ 72, 84, 96],
[117, 130, 143],
[168, 182, 196]],
[[ 0, 15, 30],
[ 48, 64, 80],
[102, 119, 136],
[162, 180, 198],
[228, 247, 266]]])
常用 einsum 操作
1 维数组
举例
a = np.arange(9)
np.einsum('i', a)
array([0, 1, 2, 3, 4, 5, 6, 7, 8])
np.einsum('i->', a)
36
np.einsum('i,i', a, a)
204
np.einsum('i,i->', a, a)
204
r = np.einsum('i,j->ij', a, a)
r
array([[ 0, 0, 0, 0, 0, 0, 0, 0, 0],
[ 0, 1, 2, 3, 4, 5, 6, 7, 8],
[ 0, 2, 4, 6, 8, 10, 12, 14, 16],
[ 0, 3, 6, 9, 12, 15, 18, 21, 24],
[ 0, 4, 8, 12, 16, 20, 24, 28, 32],
[ 0, 5, 10, 15, 20, 25, 30, 35, 40],
[ 0, 6, 12, 18, 24, 30, 36, 42, 48],
[ 0, 7, 14, 21, 28, 35, 42, 49, 56],
[ 0, 8, 16, 24, 32, 40, 48, 56, 64]])
np.sum(r)
1296
np.einsum('i,j->', a, a)
1296
2 维数组
举例
# 2d
A = np.arange(12).reshape(4,3)
B = np.arange(12).reshape(4,3)
np.einsum('ij,kj->ik', A, B)
array([[ 5, 14, 23, 32],
[ 14, 50, 86, 122],
[ 23, 86, 149, 212],
[ 32, 122, 212, 302]])
np.einsum('ij,kj->ikj', A, B).shape
(4, 4, 3)
np.einsum('ij,kl->ijkl', A, B).shape
(4, 3, 4, 3)
不同方案 PK
张量运算看着挺复杂的,但也有迹可循,而且有很多方法来实现同一个运算。最后再来一个例子,比较一下张量运算的不同实现及其效率。
- 创建一维数组
a,[0,1,...,59],将其转化为shape为(3,4,5)`` 的三维数组A` - 创建一维数组
b,[0,1,...,23],将其转化为shape为(4,3,2)的三维数组B - 将
A转置成shape为(4,3,5)的数组D - 即用两到三种方法计算如下公式:
∑ i j A j i k B i j l \large\sum_{ij} A_{jik} B_{ijl} ij∑AjikBijl
# 1 np.tensordot
A = np.arange(60.).reshape(3,4,5)
B = np.arange(24.).reshape(4,3,2)
方法一
直接使用 np.tensordot。
%%timeit
C = np.tensordot(A, B, axes=([1,0],[0,1]))
12.6 µs ± 409 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
方法二
利用 NumPy 的广播机制。
D = np.transpose(A,[1,0,2])
D.shape
(4, 3, 5)
%%timeit
np.sum(D[...,None]*B[:,:,None,:],(0,1))
5.4 µs ± 43.7 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
方法三
使用 np.einsum。
%%timeit
np.einsum('jik,ijl->kl', A, B)
2.66 µs ± 10.2 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
方法四
但这个例子比较特殊,我们可以想一个办法来进一步提高计算效率,那就是通过变形来使得可以用 dot 来代替该运算。而我们知道 dot 得到专门优化,所以效率杠杠的。但并不是所有运算都这么幸运,不一定能这么转化哦。
%%timeit
A.T.reshape(A.shape[-1], -1).dot(B.reshape(-1, B.shape[-1]))
1.94 µs ± 13.9 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
注意,计算结果都是一样的,
array([[4400., 4730.],
[4532., 4874.],
[4664., 5018.],
[4796., 5162.],
[4928., 5306.]])
最后看下这里使用的 numpy 版本,不同版本会有不同表现哦。
np.version.version
'1.15.2'
本文通过一些例子展示了爱因斯坦求和约定的强大功能,那或许你会问: 在实际写算法时怎么使用呢?自然是有大量使用的,毕竟这个工具可以完成各种复杂计算,可谓张量(高维数组)计算大杀器,具体例子留给下一篇。