基于GA优化BP神经网络的传感器故障诊断算法matlab仿真

目录

一、理论基础

二、核心程序

三、仿真测试结果

---

一、理论基础

1.做优化要先明白优化的结果是什么？

使得网络参数配置最优，测试集预测误差最小——适应度函数

2.可以通过改变什么来使得网络结果不同？

一）可以改变网络参数的初始值，再用BP神经网络的反向传播来寻得整个网络参数的最优

二）可以直接遗传算法优化整个网络参数，不引进BP来获得最佳的网络参数设置

三）可以改变参数的初始值，用遗传算法在正向传播里优化出比较好的初始参数，再用反向传播优化参数

---

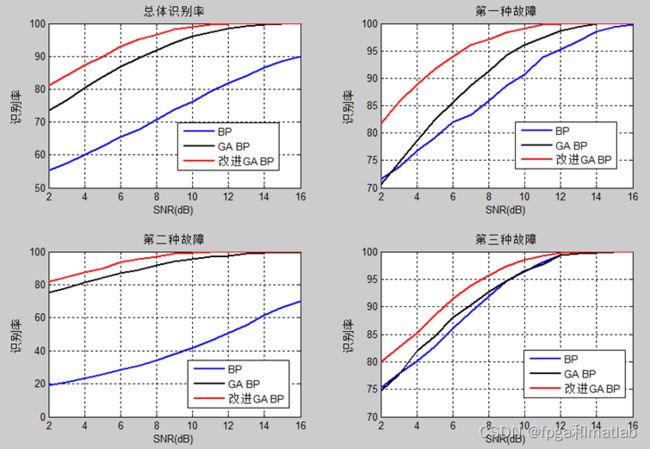
主要诊断3种故障，传感器卡死、传感器增益变化、传感器恒偏差

神经网络3层，输入神经元10个，隐层神经元6个，输出神经元3个，为了对比GA 改进BP神经网络检测方法的性能，使用Matlab建立两种方法的检测模型，一种改进后的，一种基本经典的神经网络

遗传算法稍有不同如下：

混合编码方案

二进制编码有操作简单，全局搜索能力强的优点，而实数编码的优点是精度高和效率快等。本文将二进制编码和实数编码进行了结合，发挥了各自的优点，实现了算法的优化。这种混合编码方式使得遗传效率加快、遗传搜索范围加大，同时提高了算法精度。

1. 适应度函数选取

遗传算法搜索的目标是使BP神经网络误差平方和最小的权值，而遗传算法的进化方向是向着适应值增加的方向进行，因此，适应误差的倒数为适应度函数。适应值表示为：

1. 混合选择算子

本文选择操作分为三步：（1）按适应度进行线性排序，然后随机抽取个个体，对这个个体进行交叉和变异操作；（2）保留父代的最佳个体；（3）将个子代进行交叉变异，然后子代按适应度淘汰父代最差个体。混合选择操作既可以防止算法的局部收敛，又可以保持算法的运算速度，降低了变异算子的破坏力，还能保持种群的多样性。

1. 交叉算子

交叉算子能使优良性能遗传下去，因此本文使用的方法是在二进制编码时，使用二点交叉，即随机选择两个交叉点，然后把交叉点之间的染色体进行交换。

 

二、核心程序

clc;
clear;
close all;
warning off;
addpath 'func_GA\'

rng(1);


load data.mat
Num_In     = size(Train_data,1);
Num_Hidden = 6;
Num_Out    = 1;
%构建BP网络
net        = newff(Train_data,Train_aim,Num_Hidden);
net        = func_newGA(net,Num_In,Num_Hidden,Num_Out,Train_data,Train_aim);
net        = train(net,Train_data,Train_aim);
outputs    = round(sim(net,awgn(Test_data,0,'measured')));%测试的时候，加入随机干扰

%计算整体识别率
disp('整体识别率：');
C0 = 100*length(find(outputs==Test_aim))/length(Test_aim)
disp('第1种故障识别率：');
C1 = 100*length(find(outputs(1:50)==1))/length(Test_aim)*3
disp('第2种故障识别率：');
C2 = 100*length(find(outputs(51:100)==2))/length(Test_aim)*3
disp('第3种故障识别率：');
C3 = 100*length(find(outputs(101:150)==3))/length(Test_aim)*3


%测试不同噪声大小下的识别率
SNR = 2:1:16;
for i = 1:length(SNR)
    i
    for j = 1:20
        rng(j);
        Test_data2 = awgn(Test_data,SNR(i),'measured');
        outputs    = round(sim(net,Test_data2));
        C20(i,j)     = 100*length(find(outputs==Test_aim))/length(Test_aim);
        C21(i,j)     = 100*length(find(outputs(1:50)==1))/length(Test_aim)*3;    
        C22(i,j)     = 100*length(find(outputs(51:100)==2))/length(Test_aim)*3;    
        C23(i,j)     = 100*length(find(outputs(101:150)==3))/length(Test_aim)*3; 
    end
end

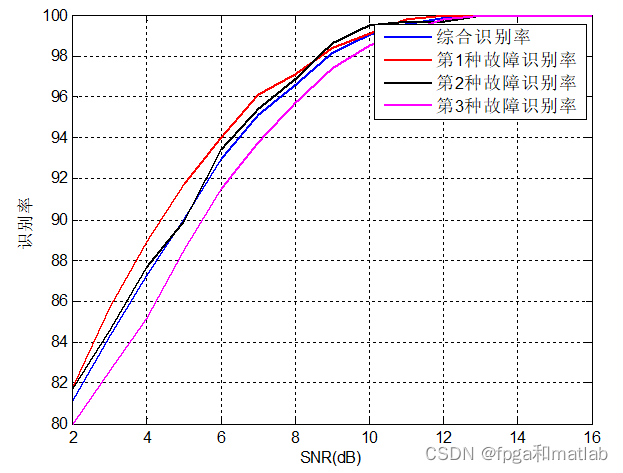
figure;
plot(SNR,mean(C20,2),'b','linewidth',2);
hold on
plot(SNR,mean(C21,2),'r','linewidth',2);
hold on
plot(SNR,mean(C22,2),'k','linewidth',2);
hold on
plot(SNR,mean(C23,2),'m','linewidth',2);
hold on
xlabel('SNR(dB)');
ylabel('识别率');
grid on
legend('综合识别率','第1种故障识别率','第2种故障识别率','第3种故障识别率');

save r2.mat SNR C20 C21 C22 C23

 

function ERR = fun(Xx,Num_In,Num_Hidden,Num_Out,net,train_data,train_aim)


%提取
L1 = 1;
L2 = Num_In*Num_Hidden;
w1 = Xx(L1:L2);

L1 = Num_In*Num_Hidden+1;
L2 = Num_In*Num_Hidden+Num_Hidden;
B1 = Xx(L1:L2);

L1 = Num_In*Num_Hidden+Num_Hidden+1;
L2 = Num_In*Num_Hidden+Num_Hidden+Num_Hidden*Num_Out;
w2 = Xx(L1:L2);

L1 = Num_In*Num_Hidden+Num_Hidden+Num_Hidden*Num_Out+1;
L2 = Num_In*Num_Hidden+Num_Hidden+Num_Hidden*Num_Out+Num_Out;
B2 = Xx(L1:L2);

net1= newff(train_data,train_aim,Num_Hidden);
%网络进化参数
net1.trainParam.showWindow = 0;
%网络权值赋值
net1.iw{1,1} = reshape(w1,Num_Hidden,Num_In);
net1.lw{2,1} = reshape(w2,Num_Out,Num_Hidden);
net1.b{1}    = reshape(B1,Num_Hidden,1);
net1.b{2}    = B2;
%网络训练
net1        = train(net1,train_data,train_aim);
outputs1    = sim(net1,train_data);
ERR1        = sum((outputs1-train_aim).^2);

ERR         = ERR1;

三、仿真测试结果

 

 A05-38