前沿
这篇论文是继承了DeepMind用图神经网络求解PDE的思路,引入了自回归方法来进行计算,加快了计算速度,并规避了自回归方法的累积误差问题。这篇文章最终发表在ICLR2022上,其中的技巧是十分简单的,但是效果非常好。
Brandstetter, J., Worrall, D., & Welling, M. (2022). Message passing neural PDE solvers. arXiv preprint arXiv:2202.03376.
图网络其实和PDE是兼容的,传统的PDE求解方法就是基于离散的方法,有限元和有限差分方法对控制欲进行了离散,也可以是做图的另一种形式。这样的话用图神经网络去学习有限元方法中的函数特征是可行,本质上是用空间换时间,用神经网络来加速PDE求解器的速度。
问题描述
本文主要考虑具有一般形式的PDE方程:
$$ \begin{array}{ll} \partial_t \mathbf{u}=F\left(t, \mathbf{x}, \mathbf{u}, \partial_{\mathbf{x}} \mathbf{u}, \partial_{\mathbf{x} \mathbf{x}} \mathbf{u}, \ldots\right) & (t, \mathbf{x}) \in[0, T] \times \mathbb{X} \\ \mathbf{u}(0, \mathbf{x})=\mathbf{u}^0(\mathbf{x}), \quad B[\mathbf{u}](t, x)=0 & \mathbf{x} \in \mathbb{X},(t, \mathbf{x}) \in[0, T] \times \partial \mathbb{X} \end{array} $$
自回归方法可以归纳为以下的方法:
$$ \mathbf{u}(t+\Delta t)=\mathcal{A}(\Delta t, \mathbf{u}(t)) $$
满足以下的初始条件:
$$ \mathcal{M}\left(t, \mathbf{u}^0\right)=\mathbf{u}(t) $$
这样的话,只要学习到微分算子\( \mathcal{A} \),那么就可以替代传统求解器了,但是面临以下的问题:
- 误差积累或者分布偏移:由于自回归方法是在时间域上迭代求解,这就会带来一个问题,就是每一步都会带来误差,这样误差就会积累,导致预测的误差越来越大甚至失败;
- 泛化性能:由于一组PDE方程代表形式相同但是参数不同的方程,这样的话如何将PDE参数进行编码使得学习到的微分算子能够快速泛化到不同的参数组上。
主要方法
这篇文章主要介绍了两个技巧去解决上面的两个问题:
时间捆绑技巧:在一次预测步骤中,同步预测未来的多个时间步长以增强稳定性和较少推理时间,与传统的求解器只预测未来一个步长不同,该方法一次向前推理\( K \)个时间步长,也就是说\( \mathbf{u}^0 \mapsto\left(\mathbf{u}^1, \mathbf{u}^2, \ldots, \mathbf{u}^K\right)=\mathbf{u}^{1: K} \),可以参考下图辅助理解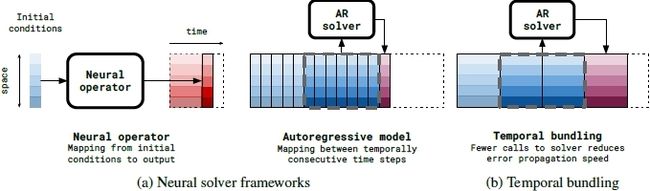
前推技巧:这个方法的核心就是对时间捆绑技巧使用\(N+1\)次,但是loss函数计算的时候只计算最后一次预测与真实的误差,也就是该算法一共预测了\( (N+1)K\)个时间步长,但是只对\( (t+N K: t+N(K+1)) \)步的时间步长范围内的误差进行计算,作者解释这样可以避免计算每部会产生的累积误差,降低计算量。为什么这么做,作者也无法解释,但是这个技巧就work了,很神奇。
文章的具体细节如下图所示,如果看不懂这个文章中的解释,直接看下面这个算法就可以了
网络架构
网络的架构就是传统的Encoder-Decoder这样的结构,非常简明易懂: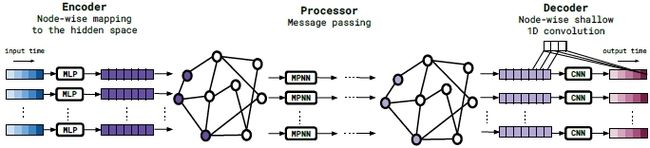
首先就是把栅格转化成图网络,然后构建Encoder,
Encoder:主要就是用多层感知机编码这些信息:\( \mathbf{f}_i^0=\epsilon^v\left(\left[\mathbf{u}_i^{k-K: k}, \mathbf{x}_i, t_k, \boldsymbol{\theta}_{\mathrm{PDE}}\right]\right) \)
Processor(消息传递机制):神经网路就是简单的多层感知机,其他没什么不同
$$ \begin{aligned} &\mathbf{m}_{i j}^m=\phi\left(\mathbf{f}_i^m, \mathbf{f}_j^m, \mathbf{u}_i^{k-K: k}-\mathbf{u}_j^{k-K: k}, \mathbf{x}_i-\mathbf{x}_j, \theta_{\mathrm{PDE}}\right) \\ &\mathbf{f}_i^{m+1}=\psi\left(\mathbf{f}_i^m, \sum_{j \in \mathcal{N}(i)} \mathbf{m}_{i j}^m, \theta_{\mathrm{PDE}}\right) \end{aligned} $$
Decoder:解码器就是CNN,具体可以参考代码,要注意输出维度的统一。首先得到一个预测向量 \( \mathbf{d}_i=\left(\mathbf{d}_i^1, \mathbf{d}_i^2, \ldots, \mathbf{d}_i^K\right) \),然后
$$ \mathbf{u}_i^{k+\ell}=\mathbf{u}_i^k+\left(t_{k+\ell}-t_k\right) \mathbf{d}_i^{\ell} $$
实验结果
实验部分作者做了大量实验,也与一些传统的求解器进行,可以看出还是具有巨大的优势,主要就是对比了五阶WENO方法,算是很经典的传统方法,推理速度确是大大加快了,我觉得上面的两个技巧其实可以迁移到别的方法上去,不知道为什么没人去尝试。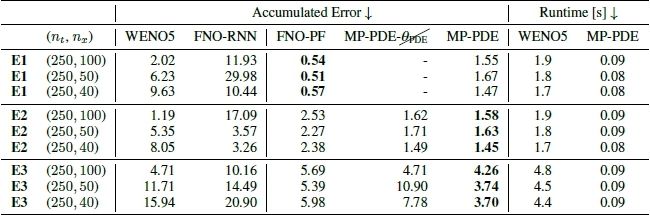
结论
这篇文章将图神经网络应用在算子学习中,还解决了自回归方法中误差积累的问题,很具有参考价值,希望作者后续能够解释前推技巧的原理。
如果读者对图网络在PDE求解器中的应用有深入的兴趣,可以继续参考以下的论文:
Horie, M., & Mitsume, N. (2022). Physics-Embedded Neural Networks: E(n)-Equivariant Graph Neural PDE Solvers. arXiv preprint arXiv:2205.11912.
Seo, S., Meng, C., & Liu, Y. (2019, September). Physics-aware difference graph networks for sparsely-observed dynamics. In International Conference on Learning Representations.
Iakovlev, V., Heinonen, M., & Lähdesmäki, H. (2020). Learning continuous-time PDEs from sparse data with graph neural networks. arXiv preprint arXiv:2006.08956.
Belbute-Peres, F. D. A., Economon, T., & Kolter, Z. (2020, November). Combining differentiable PDE solvers and graph neural networks for fluid flow prediction. In International Conference on Machine Learning (pp. 2402-2411). PMLR.