用C++写一个《炸飞机》/《死亡轰炸》游戏辅助程序

游戏介绍

最近和女朋友因为异地恋而开始寻找可以远程一起玩的游戏，就发现了同桌派对这个App，里面有一个游戏叫做《死亡轰炸》（又名《炸飞机》）特别有意思，游戏规则是这样的：

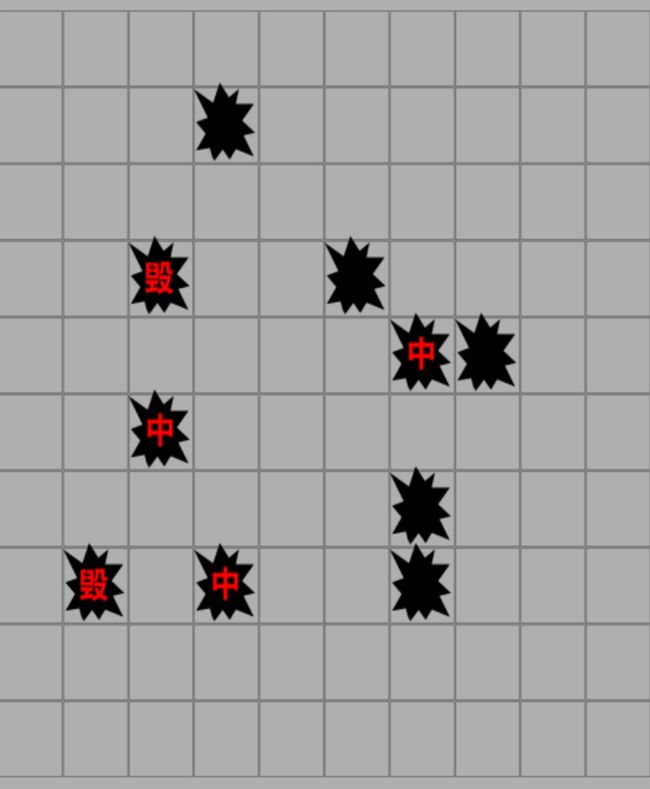
典型的地图大小是 10 × 10，飞机数目为3个，飞机的形状是一个“士”字形。在游戏一开始我们要摆好自己的飞机（飞机之间不能有重叠的地方），游戏开始之后，我们可以选择对方地图的位置进行轰炸，轰炸后会提示该位置为“空地”、“机身”或“机头”三种类型。当我们炸毁对方的所有机头，就获得胜利。

在玩了许久之后，我突发奇想，能不能用计算机去算出一个最优轰炸策略（或者接近最优）。于是便开始了长达三个小时的思考和写代码。

算法

我一开始认为可以用计算机去算，是因为地图很小飞机很少，就算全部枚举出可能性也能处理过来。因此我首先定义了一个结构体 node 去记录某一种可能，node 里面保存了地图数组，数组元素是每个位置的类型（unknown, empty, plane, planeHead）。然后就是 DFS 遍历出所有可能的情况并且保存下来，这部分不详细展开，总之最后找出了 66816 种摆放方式。

总体的思路是这样的：首先保存下所有的可能，然后每一步决定一个轰炸位置，这个轰炸位置由当前局面和可能集合共同决定，直到找到所有 planeHead 为止。因此最核心的就是每一步应该遵循怎样的策略？

最贪心的想法就是，找到一个轰炸位置，使得选择它之后能够排除尽可能多的可能，也就是：

找到一个期望收益最大的位置，这里的收益表示通过轰炸这个位置能够减少的可能数目

每个轰炸位置只有三种情况，我们假设这个位置为 empty, plane 和 planeHead 的概率分别为 $p_1$, $p_2$ 和 $p_3$，当前可能集合的大小为 $N$ ，那么选择这个位置进行轰炸的期望收益就是：
$$E=p_1\ast (p_{2}N+p_{3}N)+p2\ast (p_{1}N+p_{3}N)+p_3\ast (p_{1}N+p_{2}N)$$
而每个概率则可以通过枚举每一种可能来统计得出（注意每一个决策步骤中这三个概率是不一样的）。执行完每一步之后，通过真实的结果去更新当前局面和可能集合。最终可以非常快地找出所有机头。

结果

运行结果是这样的：

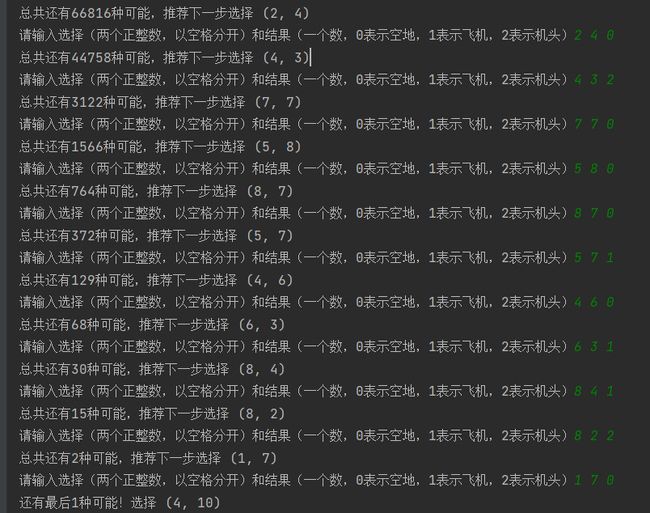
用这个程序去跟别人对战基本上没输过吧，然后我发现程序跟人的思路有很大的不同。我自己玩的话如果找到了一个机身，就会在机身周围不停地轰炸，因此最后会找到很多机身，而程序会找到更多的空地。

改进的方面

1. 有时候会存在多个期望收益相同的位置，可以让程序优先选择非空地的地方；
2. 本来收益表示的是减少的可能数目，或许可以变成减少的可能数目和剩下的可能数目的比值。

代码

#include 
#include 
#include 
#include 

using namespace std;

#define N 10    // 地图边长
#define P_NUM 3  // 飞机数目

typedef pair<int, int> pos;

enum mapType {
    unknown,
    empty,
    plane,
    planeHead,
};

struct node {
    mapType map[N + 1][N + 1] = {empty};

    long long hash() {
        long long M = 10000000000037, p = 107;
        long long ret = 1;
        for (int i = 1; i <= N; i++)
            for (int j = 1; j <= N; j++)
                if (map[i][j] == planeHead || map[i][j] == plane)
                    ret = ret * (i * N + j) % M * p % M;
        return ret;
    }
};

void printNode(node x) {
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= N; j++) {
            if (x.map[i][j] == empty) cout << "_";
            else if (x.map[i][j] == plane) cout << "*";
            else if (x.map[i][j] == planeHead) cout << "&";
            cout << " ";
        }
        cout << endl;
    }
}


mapType a[N + 1][N + 1] = {empty};
int upPlane[10][2] = {+1, -2, +1, -1, +1, 0, +1, +1, +1, +2, +2, 0, +3, -1, +3, 0, +3, +1};
int downPlane[10][2] = {-1, -2, -1, -1, -1, 0, -1, +1, -1, +2, -2, 0, -3, -1, -3, 0, -3, +1};
int leftPlane[10][2] = {-2, +1, -1, +1, 0, +1, +1, +1, +2, +1, 0, +2, -1, +3, 0, +3, +1, +3};
int rightPlane[10][2] = {-2, -1, -1, -1, 0, -1, +1, -1, +2, -1, 0, -2, -1, -3, 0, -3, +1, -3};

void dfs(int nowPNum, vector<node> &VN) {
    if (nowPNum > P_NUM) {
        node x;
        // copy(begin(a), end(a), begin(x.map));
        memcpy(x.map, a, sizeof(a));
        VN.push_back(x);
        return;
    }
    /**
     * 枚举当前这架飞机的所有可能位置
     * 总共4种情况，即对应飞机的4种朝向，每种情况枚举机头位置
     */
    mapType b[N + 1][N + 1];
    memcpy(b, a, sizeof(a));   // 备份数组a

    for (int dir = 0; dir < 4; dir++)   // 枚举飞机朝向
        for (int i = 1; i <= N; i++)
            for (int j = 1; j <= N; j++) {  // 枚举机头位置
                memcpy(a, b, sizeof(b));   // 首先初始化数组a
                bool flag = true;
                if (a[i][j] != empty) continue;
                a[i][j] = planeHead;
                for (int k = 0; k < 9; k++) {   // 枚举机身位置
                    int ii, jj;
                    if (dir == 0) ii = i + upPlane[k][0], jj = j + upPlane[k][1];
                    else if (dir == 1) ii = i + downPlane[k][0], jj = j + downPlane[k][1];
                    else if (dir == 2) ii = i + leftPlane[k][0], jj = j + leftPlane[k][1];
                    else ii = i + rightPlane[k][0], jj = j + rightPlane[k][1];
                    if (ii < 1 || ii > N || jj < 1 || jj > N) {
                        flag = false;
                        break;
                    };
                    if (a[ii][jj] != empty) {
                        flag = false;
                        break;
                    };
                    a[ii][jj] = plane;
                }
                if (flag) dfs(nowPNum + 1, VN);
            }
}

vector<node> initNodes() {
    /**
     * 给出所有可能的摆放方式（已去重）
     */
    for (int i = 1; i <= N; i++)
        for (int j = 1; j <= N; j++)
            a[i][j] = empty;

    vector<node> temp, ret;
    dfs(1, temp);
    set<long long> s;   // 用于去重
    for (node x:temp) {
        long long h = x.hash();
        if (!s.count(h)) {
            ret.push_back(x);
            s.insert(h);
        }
    }
    return ret;
}

pos getNextStep(const vector<node> &s, mapType nowMap[N + 1][N + 1]) {
    int ii = 0, jj = 0, maxEarn = 0;
    for (int i = 1; i <= N; i++)
        for (int j = 1; j <= N; j++)
            if (nowMap[i][j] == unknown) {  // 枚举可以选的位置
                // 首先计算当前位置各种情况的频率
                int p1 = 0, p2 = 0, p3 = 0;
                for (node x:s) {
                    if (x.map[i][j] == planeHead) p2++;
                    if (x.map[i][j] == plane) p1++;
                    if (x.map[i][j] == empty) p3++;
                }
                int earn = p3 * (p1 + p2) + p2 * (p1 + p3) + p1 * (p2 + p3);
                if (earn > maxEarn) {
                    ii = i, jj = j;
                    maxEarn = earn;
                }
            }
    return make_pair(ii, jj);
}

void elimination(vector<node> &s, int x, int y, mapType m) {
    vector<node> temp;
    temp.reserve(s.size());
    for (node t:s) temp.push_back(t);
    s.clear();
    for (node t:temp) {
        if (t.map[x][y] == m) s.push_back(t);
    }
}

int main() {
    vector<node> s = initNodes();
    mapType nowMap[N + 1][N + 1] = {unknown};

    while (s.size() > 1) {
        cout << "总共还有" << s.size() << "种可能，";
        pos p = getNextStep(s, nowMap);
        cout << "推荐下一步选择 (" << p.first << ", " << p.second << ")" << endl;
        int x, y, res;
        do {
            cout << "请输入选择（两个正整数，以空格分开）和结果（一个数，0表示空地，1表示飞机，2表示机头）";
            cin >> x >> y >> res;
        } while (x < 1 || x > N || y < 1 || y > N || res < 0 || res > 2);
        if (res == 0) nowMap[x][y] = empty, elimination(s, x, y, mapType::empty);
        else if (res == 1) nowMap[x][y] = plane, elimination(s, x, y, mapType::plane);
        else if (res == 2) nowMap[x][y] = planeHead, elimination(s, x, y, mapType::planeHead);
    }
    // 最后一步
    cout << "还有最后1种可能！选择 ";
    node x = *s.begin();
    for (int i = 1; i <= N; i++)
        for (int j = 1; j <= N; j++)
            if (x.map[i][j] == planeHead && nowMap[i][j] == unknown) {
                cout << "(" << i << ", " << j << ")  ";
            }

    return 0;
}