简单遗传算法 + 最低水平线算法求解二维排样问题

前言

笔者之前有两篇文章分别介绍了最低水平线算法（点击传送门）和简单遗传算法（点击传送门），
本文在此基础上将最低水平线算法和简单遗传算法相结合来求解二维排样问题。

编码

由于板材和零件都是矩形，为了使矩形排放时板材的利用率尽可能高，每个零件在具体排放时只能有横放和竖放两种方式。由于每个基因的编码可以为正或负，在本文中统一规定矩形的编号为正表示矩形不进行在所排平面内的90度旋转，编号为负表示矩形在排样时要在所排平面内做90度旋转，
如染色体 (-2，1，5，3，4) 表示2号矩形需要做旋转，而其他矩形则正常排放，如下图。

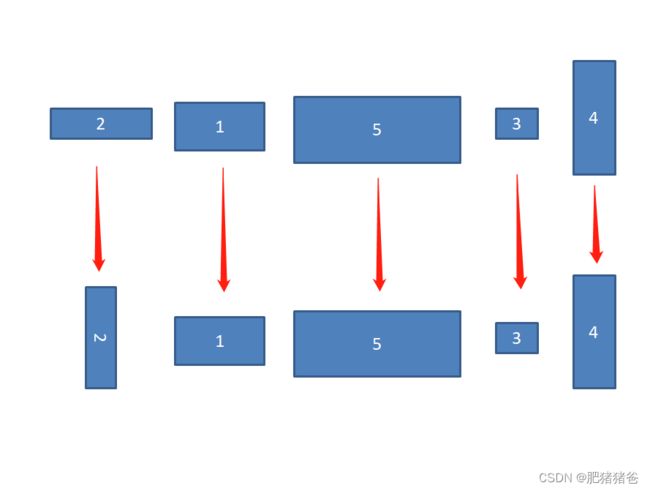
设要排放的矩形总数为n，n个矩形的编号构成了一个染色体。种群中每条染色体的长度与待排矩形零件总数相同，染色体中每个基因的编码对应相应矩形的编号，所有基因编码的一个排列顺序构成了一个染色体。

适应度

本文选择的适应度是排样序列经过最低水平线算法排样后的利用率，利用率越高，个体适应度越好

交叉操作

本文采用的染色体交叉方法具体如下：
先选一个固定的交叉位置，在该点以前的基因不变，在该点以后的基因部分进行交叉。将两条染色体的不交叉的基因部分进行比较，在去掉两个基因片断中相同的基因后，将染色体不交叉部分剩下的基因按原来的顺序分别放入两个数组p和q中。在对染色体交叉部分的基因片断进行操作时，对不等于数组p或q中的基因直接进行交换。对于与数组中的基因相同的基因，则先换成对应的数组p或q中的基因后再进行交换。

例如要进行交叉的两个染色体分别为A={3，2，4，5，9，8，7，6，1，10}，B={9，1，10，3，2，5，4，6，7，8}，染色体交叉的具体步骤如下:

1. 先确定一个交叉位置，假如选择第五个位置(每条染色体最左边的基因，其位置规定为1，从左向右，位置编号依次增加)为交叉点，图中箭头所在位置代表交叉点；
   
2. 对比A染色体和B染色体的不变部分，两者都有的基因位是3、2、9，将A染色体不变部分的基因片断去掉3、2、9，将剩下的基因部分按原来的顺序放入数组p={4，5}，同理将B染色体不变部分的基因片断中去掉3、2、9，将剩下的基因部分按原来的顺序放入数组q={1，10}；
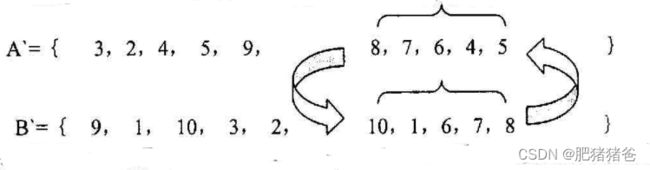
3. 对比A染色体和B染色体的交叉部分，两者不相同的部分：A染色体为1、10；B为5、4，分别替换为对应的数组p或q中的基因，这时A染色体的交叉部分变为{8，7，6，4，5}，B染色体交叉部分变成{10，1，6，7，8 }；
4. 经过步骤3，这时的A染色体和B染色体分别变为：
   

对两条染色体的后半部分进行交换，得到交叉操作后最终形成的两条新染色体；

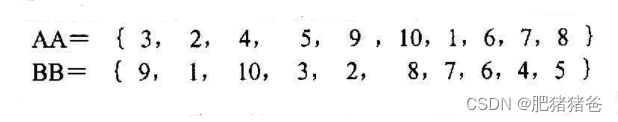
变异操作

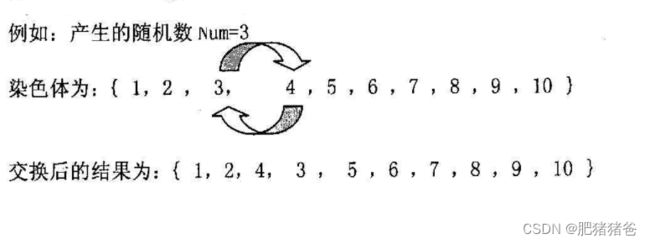
本文变异操作选择交换变异，具体步骤：产生[1，n]之间的一个随机数 Num，将该数和紧随其后的数相互交换；如果该数是染色体中的最后一个数，则将该数与染色体中的第一个数相交换。

代码及运行结果（笔者运行环境为python3.7）

import random
import copy
import numpy as np
import matplotlib.pyplot as plt
import math

# 个体长度（待排样箱体个数）
CHROM_LEN = 26
# 种群大小
POP_SIZE = 40
# 最大遗传代数
MAX_GENERATION = 100
# 交叉概率
PC = 0.7
# 变异概率
PM = 0.05


# 水平线类（起始x位置，终止x位置，高度）
class OutLine:
    def __init__(self, origin, end, height):
        self.origin = origin
        self.end = end
        self.height = height

    def __str__(self):
        return "OutLine:origin:{}, end:{}, height:{}".format(self.origin, self.end, self.height)


# 矩形物品类（宽度，高度，编号）
class Product:
    def __init__(self, w, h, num=0):
        self.w = w
        self.h = h
        self.num = num

    def __str__(self):
        return "product:w:{}, h:{}, num:{}".format(self.w, self.h, self.num)

    # 旋转90度并返回新对象
    def rotate_new(self):
        return Product(self.h, self.w, self.num)


# 布局类
class RectLayout:
    def __init__(self, width, line_list=[]):
        # 容器宽度
        self.width = width
        # 水平线集合（起始x位置，终止x位置，高度）
        self.line_list = line_list
        # 水平线（起始x位置，终止x位置，高度）
        self.lowest_line = None
        # 水平线索引（起始x位置，终止x位置，高度）
        self.lowest_line_idx = 0
        # 最终位置结果[[矩形件编号,左下角横坐标,左下角纵坐标,矩形件宽度,矩形件高度], ...]
        self.result_pos = []
        # 板材利用率
        self.ratio = 0.0

    # 初始化水平线集合（起始x位置，终止x位置，高度）
    def init_line_list(self, origin, end, height):
        init_line = OutLine(origin, end, height)
        self.line_list = [init_line]
        self.lowest_line = init_line
        self.lowest_line_idx = 0

    # 提升最低水平线
    def enhance_line(self, index):
        if len(self.line_list) > 1:
            # 获取高度较低的相邻水平线索引，并更新水平线集
            neighbor_idx = 0
            if index == 0:
                neighbor_idx = 1
            elif index + 1 == len(self.line_list):
                neighbor_idx = index - 1
            else:
                # 左边相邻水平线
                left_neighbor = self.line_list[index - 1]
                # 右边相邻水平线
                right_neighbor = self.line_list[index + 1]
                # 选择高度较低的相邻水平线，左右相邻水平线高度相同时，选择左边相邻的水平线
                if left_neighbor.height < right_neighbor.height:
                    neighbor_idx = index - 1
                elif left_neighbor.height == right_neighbor.height:
                    if left_neighbor.origin < right_neighbor.origin:
                        neighbor_idx = index - 1
                    else:
                        neighbor_idx = index + 1
                else:
                    neighbor_idx = index + 1
            # 选中的高度较低的相邻水平线
            old = self.line_list[neighbor_idx]
            # 更新相邻水平线
            if neighbor_idx < index:
                self.line_list[neighbor_idx] = OutLine(old.origin, old.end + self.line_width(index), old.height)
            else:
                self.line_list[neighbor_idx] = OutLine(old.origin - self.line_width(index), old.end, old.height)
            # 删除当前水平线
            del self.line_list[index]

    # 按位置更新水平线
    def update_line_list(self, index, new_line):
        self.line_list[index] = new_line

    # 按位置插入水平线（插在某索引位置后面）
    def insert_line_list(self, index, new_line):
        new_lists = []
        if len(self.line_list) == index + 1:
            new_lists = self.line_list + [new_line]
        else:
            new_lists = self.line_list[:index + 1] + [new_line] + self.line_list[index + 1:]
        self.line_list = new_lists

    # 计算水平线宽度
    def line_width(self, index):
        line = self.line_list[index]
        return line.end - line.origin

    # 找出最低水平线（如果最低水平线不止一条则选取最左边的那条）
    def find_lowest_line(self):
        # 最低高度
        lowest = min([_l.height for _l in self.line_list])
        # 最低高度时，最小开始横坐标
        origin = min([_l.origin for _l in self.line_list if _l.height == lowest])
        for _idx, _line in enumerate(self.line_list):
            if _line.height == lowest and _line.origin == origin:
                self.lowest_line_idx = _idx
                self.lowest_line = _line

    # 清空水平线集合
    def empty_line_list(self):
        self.line_list.clear()

    # 计算最高水平线高度，即所用板材最大高度
    def cal_high_line(self):
        max_height = max([ll.height for ll in self.line_list])
        return max_height

    # 将矩形物品排样
    def packing(self, _pro: Product):
        # 最低水平线宽度
        lowest_line_width = self.line_width(self.lowest_line_idx)
        # 对矩形件排样
        self.result_pos.append([_pro.num, self.lowest_line.origin, self.lowest_line.height, _pro.w, _pro.h])
        # 更新水平线集
        new_line1 = OutLine(self.lowest_line.origin, self.lowest_line.origin + _pro.w, self.lowest_line.height + _pro.h)
        new_line2 = OutLine(self.lowest_line.origin + _pro.w, self.lowest_line.origin + lowest_line_width, self.lowest_line.height)
        self.update_line_list(self.lowest_line_idx, new_line1)
        if lowest_line_width - _pro.w > 0:
            self.insert_line_list(self.lowest_line_idx, new_line2)

    # 计算板材利用率
    def cal_used_ratio(self):
        # 计算板材利用率
        used_area = 0
        for _p in self.result_pos:
            used_area += _p[3] * _p[4]
        # 板材使用最大高度
        max_high = self.cal_high_line()
        # 利用率
        if max_high > 0:
            self.ratio = round((used_area * 100) / (self.width * max_high), 3)
        return used_area, self.ratio


# 排样主算法
def packing_main(seq, container_width, products):
    # 初始化布局类
    layout = RectLayout(width=container_width)
    layout.empty_line_list()
    layout.result_pos.clear()
    # 初始化水平线集
    layout.init_line_list(0, container_width, 0)
    # 循环直到把所有物品都排完
    while seq:
        candidate_idx = seq[0]
        _idx = int(math.fabs(int(candidate_idx)))
        # 候选物品
        pro = products[_idx]
        # 最低水平线及其索引
        layout.find_lowest_line()
        # 可用长度
        available_width = layout.line_width(layout.lowest_line_idx)
        # 对应的装箱编号为负数时，对矩形件进行旋转
        if int(candidate_idx) < 0:
            pro = pro.rotate_new()
        if available_width >= pro.w:
            # 将候选物品排样
            layout.packing(pro)
            # 剔除已经排样的物品
            seq.remove(candidate_idx)
        else:
            # 最低水平线宽度小于要排样矩形宽度，提升最低水平线
            layout.enhance_line(layout.lowest_line_idx)
    # 计算板材利用率
    _area, _ratio = layout.cal_used_ratio()
    # 计算最高水平线高度，即所用板材最大高度
    container_height = layout.cal_high_line()
    return layout, _ratio, container_height


# 对排样序列洗牌，并随机对物品进行旋转
def shuffle_seq(seq):
    # 洗牌
    random.shuffle(seq)
    # 新的序列
    new_seq = []
    for s in seq:
        # 随机数
        r = np.random.rand()
        # 随机对物品进行旋转
        if r < 0.5:
            new_seq.append(0 - s)
        else:
            new_seq.append(s)
    return new_seq


# 遗传算法个体类
class Individual:
    def __init__(self, chrom: str):
        # 基因序列
        self.chrom = chrom
        # 适应度
        self.fitness = 0

    # 计算个体适应度
    def get_fitness(self, container_width, products):
        _, r, _ = packing_main(copy.copy(self.chrom.split(",")), container_width, products)
        self.fitness = r
        return self.fitness

    def __str__(self):
        return "chrom:{}, fitness:{}".format(self.chrom, self.fitness)


# 获得当代最佳和最差个体索引
def best_and_worst(population):
    # 最佳个体索引
    best_idx = 0
    # 最差个体索引
    worst_idx = 0
    for _idx, p in enumerate(population):
        if p.fitness > population[best_idx].fitness:
            best_idx = _idx
        elif p.fitness < population[worst_idx].fitness:
            worst_idx = _idx
    return best_idx, worst_idx


# 选择（复制）操作
def select(population):
    # 新种群
    new_pop = []
    # 当代个体适应度总和
    fitness_sum = max(sum([i.fitness for i in population]), 0.0001)
    # 当代个体累计适应度占比
    cfitness = []
    # 计算相对适应度占比
    for j in range(POP_SIZE):
        cfitness.append(population[j].fitness / fitness_sum)
    # 计算累计适应度占比
    for j in range(POP_SIZE):
        if j == 0:
            continue
        cfitness[j] = cfitness[j-1] + cfitness[j]
    # 依据累计适应度占比进行选择复制，随机数大于对应的累计适应度占比，则进行复制
    for k in range(POP_SIZE):
        index = 0
        while random.random() > cfitness[index]:
            index += 1
            # 若无法找到要复制的其他个体，则沿用当前个体
            if index >= POP_SIZE:
                index = k
                break
        new_pop.append(copy.deepcopy(population[index]))
    return new_pop


# 两个个体进行交叉操作
def crossover_inner(individual1: Individual, individual2: Individual, position: int):
    # 两个个体染色体相同，则不进行交叉
    if (np.array(individual1.chrom.split(",")) == np.array(individual2.chrom.split(","))).all():
        return
    # 两个个体基因型列表
    _chrom1 = individual1.chrom.split(",")
    _chrom2 = individual2.chrom.split(",")
    # 两个个体各自基因型列表中元素对应的正负号    
    flag_table1 = {int(math.fabs(int(c))): 1 if int(c) >= 0 else -1 for c in _chrom1}
    flag_table2 = {int(math.fabs(int(c))): 1 if int(c) >= 0 else -1 for c in _chrom2}
    # 两个个体去掉正负号的排样序列
    chrom1 = [int(math.fabs(int(ch))) for ch in _chrom1]
    chrom2 = [int(math.fabs(int(ch))) for ch in _chrom2]
    # 不交叉部分排样物品序号的交集
    intersection1 = list(set(chrom1[:position]).intersection(set(chrom2[:position])))
    # 不交叉部分中，个体1对于个体2的物品序号差集
    diff1 = []
    # 不交叉部分中，个体2对于个体1的物品序号差集
    diff2 = []
    # 不交叉部分排样物品序号均相同
    if len(intersection1) == position:
        # 直接交换
        cross_gene1 = _chrom1[position:]
        cross_gene2 = _chrom2[position:]
        individual1.chrom = ",".join(_chrom1[:position] + cross_gene2)
        individual2.chrom = ",".join(_chrom2[:position] + cross_gene1)
        return
    # 不交叉部分排样物品序号均不相同
    elif len(intersection1) == 0:
        diff1 = chrom1[:position]
        diff2 = chrom2[:position]
    else:
        diff1 = [c for c in chrom1[:position] if c not in intersection1]
        diff2 = [c for c in chrom2[:position] if c not in intersection1]
    # 物品序号转换表
    table = dict()
    for _idx, d in enumerate(diff1):
        table[d] = diff2[_idx]
    for _idx, d in enumerate(diff2):
        table[d] = diff1[_idx]
    # 交叉部分排样物品序号的交集
    intersection2 = list(set(chrom1[position:]).intersection(set(chrom2[position:])))
    # 转换排样序号，使最终交叉后的基因型合法
    for i, v in enumerate(chrom1):
        if i >= position and v not in intersection2 and v in table:
            _chrom1[i] = table[v] * flag_table2[table[v]]
    for i, v in enumerate(chrom2):
        if i >= position and v not in intersection2 and v in table:
            _chrom2[i] = table[v] * flag_table1[table[v]]
    # 需要交换的基因
    cross_gene1 = _chrom1[position:]
    cross_gene2 = _chrom2[position:]
    individual1.chrom = ",".join([str(c) for c in _chrom1[:position] + cross_gene2])
    individual2.chrom = ",".join([str(c) for c in _chrom2[:position] + cross_gene1])


# 交叉操作
def crossover(population):
    # 随机产生个体配对索引，类似于洗牌的效果
    index = [i for i in range(POP_SIZE)]
    for i in range(POP_SIZE):
        point = random.randint(0, POP_SIZE - i - 1)
        temp = index[i]
        index[i] = index[point + i]
        index[point + i] = temp
    for i in range(0, POP_SIZE, 2):
        if random.random() > PC:
            # 随机选择交叉开始位置
            cross_start = random.randint(0, CHROM_LEN - 2) + 1
            # 两个个体染色体交叉
            crossover_inner(population[index[i]], population[index[i + 1]], cross_start)


# 变异操作
def mutation(population):
    for individual in population:
        # 新染色体
        new_chrom_ch = individual.chrom.split(",")
        for i in range(CHROM_LEN):
            # 随机数小于变异概率，则进行变异操作
            if random.random() < PM:
                # 变异位置
                p = random.randint(0, CHROM_LEN-1)
                # 交换变异
                next = 0 if p == CHROM_LEN-1 else p+1
                temp = new_chrom_ch[p]
                new_chrom_ch[p] = new_chrom_ch[next]
                new_chrom_ch[next] = temp
                # 随机产生旋转效果
                if np.random.rand() < 0.5:
                    new_chrom_ch[p] = str(0 - int(new_chrom_ch[p]))
        # 更新染色体
        individual.chrom = ",".join(new_chrom_ch)


# 绘制排样结果
def draw_packing_result(layout: RectLayout, container_width, container_height):
    # 绘制排样布局
    fig = plt.figure()
    plt.xlim(0, container_width)
    plt.ylim(0, container_height)
    plt.axis("off")
    ax = fig.add_subplot(111, aspect='equal')
    ax.set_xlim(0, container_width)
    ax.set_ylim(0, container_height)

    for pos in layout.result_pos:
        ax.add_patch(
            plt.Rectangle(
                (pos[1], pos[2]),  # 矩形左下角
                pos[3],  # 长
                pos[4],  # 宽
                alpha=1,
                edgecolor='black',
                linewidth=1
            )
        )
        # 物品编号
        ax.text(pos[1] + pos[3] / 2 - 0.5, pos[2] + pos[4] / 2 - 0.3, "{}".format(pos[0]), transform=ax.transData)

    # plt.show()
    plt.savefig('lowest_horizontal_line_sga1.png', dpi=800)


# 绘制进化过程
def draw_evolution(evolution):
    x = [i for i in range(len(evolution))]
    # 清空画布
    plt.clf()
    plt.plot(x, evolution)
    # plt.show()
    plt.savefig('lowest_horizontal_line_sga2.png', dpi=800)


# 主方法
def main():
    # 板材宽度
    container_width = 10
    # 初始化矩形物品尺寸，也可以随机生成
    # item_sizes = np.random.randint(1, 8, size=(CHROM_LEN, 2)).tolist()
    item_sizes = [[3, 1], [4, 4], [1, 1], [2, 3], [2, 4], [3, 4], [1, 4], [2, 2], [3, 3], [3, 1], [4, 2], [3, 1],
                  [3, 1], [3, 2], [4, 2], [1, 2], [1, 3], [3, 4], [2, 3], [1, 1], [2, 1], [3, 2], [4, 3], [3, 2],
                  [4, 3], [4, 3]]
    # 物品id（仅作为显示使用）
    ran = [i + 1 for i in range(len(item_sizes))]
    # 矩形物品列表
    products = []
    for idx in range(CHROM_LEN):
        products.append(Product(item_sizes[idx][0], item_sizes[idx][1], ran[idx]))
    # 种群
    population = []
    # 初始化种群
    seq_seed = [i for i in range(len(item_sizes))]
    temp = copy.copy(seq_seed)
    for _ in range(POP_SIZE):
        population.append(Individual(",".join([str(t) for t in temp])))
        # 打乱初始排样顺序
        temp = shuffle_seq(temp)
    # 计算初始种群适应度
    for individual in population:
        individual.get_fitness(container_width, products)
    # 初始种群最佳和最差个体
    best_idx, worst_idx = best_and_worst(population)
    # 历史最佳个体
    current_best = population[best_idx]
    # 进化过程，每一代最佳个体对应的利用率
    evolution = []
    # 循环直到最大代数
    for generation in range(MAX_GENERATION):
        # 选择复制
        population = select(population)
        # 交叉
        crossover(population)
        # 变异
        mutation(population)
        # 重新计算适应度
        for individual in population:
            individual.get_fitness(container_width, products)
        # 当代种群最佳和最差个体索引
        best_idx, worst_idx = best_and_worst(population)
        # 利用精英模型执行进化操作，用历史最佳个体代替当代的最差个体
        if population[best_idx].fitness > current_best.fitness:
            current_best = population[best_idx]
        else:
            population[worst_idx] = current_best
        # 更新进化过程
        _, _f, _ = packing_main(copy.copy(current_best.chrom.split(",")), container_width, products)
        evolution.append(_f)
    # 打印最佳个体信息
    print(current_best)
    best_layout, _, best_container_height = packing_main(copy.copy(current_best.chrom.split(",")), container_width, products)
    # 绘制排样布局
    draw_packing_result(best_layout, container_width, best_container_height)
    # 绘制进化过程
    draw_evolution(evolution)


if __name__ == "__main__":
    main()

绘制的排样结果图如下（由于初始种群的随机性，每一次执行产生的结果可能会不同）：

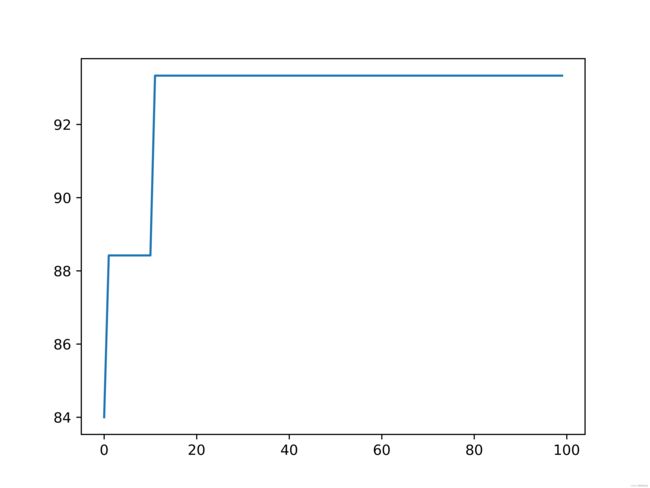
每一代最优解的进化过程如下图所示（由于初始种群的随机性，每一次执行产生的结果可能会不同）：

本文理论部分摘自广西师范大学的硕士论文《矩形件下料优化排样的遗传算法》，论文作者和导师都很牛，读者可以自行百度获取论文原文。

笔者水平有限，若有不对或可以优化的地方欢迎评论留言。