【图像处理】 常用边缘检测算法对比分析

边缘的定义

首先介绍什么是边缘。在数字图像中，边缘是指图像局部变化最显著的部分，边缘主要存在于目标与目标，目标与背景之间，是图像局部特性的不连续性，如灰度的突变、纹理结构的图标、颜色的图标等。尽管图像的边缘点产生的原因各不相同，但他们都是图形上灰度不连续或灰度几句辩护的点，图像边缘分为阶跃状、斜坡状和屋顶状。

边缘检测的基本方法

一般图像边缘检测方法主要有如下四个步骤：

图像滤波

传统边缘检测算法主要是基于图像强度的一阶和二阶导数，但导数的计算对噪声很敏感，因此必须使用滤波器来改善与噪声有关的边缘检测器的性能。需要指出的是，大多数滤波器在降低噪声的同时也造成了了边缘强度的损失，因此，在增强边缘和降低噪声之间需要一个折衷的选择。

图像增强

增强边缘的基础是确定图像各点邻域强度的变化值。增强算法可以将邻域(或局部)强度值有显著变化的点突显出来。边缘增强一般是通过计算梯度的幅值来完成的。

图像检测

在图像中有许多点的梯度幅值比较大，而这些点在特定的应用领域中并不都是边缘，所以应该用某种方法来确定哪些点是边缘点。最简单的边缘检测判断依据是梯度幅值。

图像定位

如果某一应用场合要求确定边缘位置，则边缘的位置可在子像素分辨率上来估计，边缘的方位也可以被估计出来。近20多年来提出了许多边缘检测算子，在这里我们仅讨论集中常见的边缘检测算子。

常见边缘检测算子分析

1) 差分边缘检测

处理数字图像的离散域时，可以用图像的一阶差分来代替图像函数的导数。
定义二维离散图像函数在 X 轴方向的一阶差分为：
f(i+1,j)-f(i,j) (2.3.1)
Y轴方向上的一阶差分定义为：

f(i,j+1)-f(i,j) (2.3.2)

利用图像灰度的一阶导数算子在灰度值变化显著的地方得到的极值来检测边缘点。它在某一个点的值就代表了该点的边缘强度值，可通过设置阈值来进一步得到边缘图像。但用差分的方法进行边缘检测必须使差分的方向和边缘的方向相垂直，这就需要对图像的不同方向分别进行差分运算，增加了运算量。一般可将边缘分为水平边缘、垂直边缘和对角线边缘：

显然，差分边缘是最原始、最基础的方法，这种算子具有方向性，并且由于计算不方便等原因，在现在已经很少应用了，但其思想还是很多其他算法的基础。

2）Reborts算子

Reboerts算子是一种利用局部差分来寻找边缘的算子，Roberts 梯度算子所采用的是对角方向相邻两像素值之差，算子形式如下：

Gx = f(i,j) - f(i-1,j-1) (2.3.3)
Gy = f(i-1,j) - f(i,j-1) (2.3.4)
|G(x,y)| = sprt(Gx²+Gy²) (2.3.5)
Roberts梯度算子对应的卷积模版为：

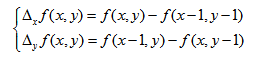
图像算法 - 常用边缘检测算法对比分析 - dingmz_frc - dingmz_frc的博客
用以上两个卷积算子与图像运算后，可求出图像的梯度幅值 G ( x,y)，然后选择
适当的阈值τ ,若 G ( x,y)>τ，则 (i ,j)为边缘点，否则，判断 (i ,j)为非边缘点。由此得到一个二值图像 { g (i,j)}，即边缘图像。Roberts 算子采用的是用对角线方向上相邻两像素的差近似梯度幅值来检测边缘，它的定位精度高，对于水平和垂直方向的边缘，检测效果较好，而对于有一定倾角的斜边缘，检测效果则不理想，存在着许多的漏检。另外，在含噪声的情况下，Roberts 算子不能有效的抑制噪声，容易产生一些伪边缘。因此，该算子适合于对低噪声且具有陡峭边缘的图像提取边缘。

Roberts算子采用对角线方向相邻两像素之差近似梯度幅值检测边缘。检测水平和垂直边缘的效果好于斜向边缘，定位精度高，对噪声敏感

3）Sobel算子

Sobel算子在边缘检测算子扩大了其模版，在边缘检测的同时尽量削弱了噪声。其模版大小为3×3，其将方向差分运算与局部加权平均相结合来提取边缘。在求取图像梯度之前，先进行加权平均，然后进行未分，加强了对噪声的一致。
图像中的每个像素点和以上水平和垂直两个卷积算子做卷积运算后，再计算得到
梯度幅值 G ( x,y)，然后选取适当的阈值τ ，若 G ( x,y)>τ，则 (i ,j)为边缘点，否则，判断 (i ,j)为非边缘点。由此得到一个二值图像 { g (i,j)}，即边缘图像。Sobel 算子在空间上比较容易实现，不但产生较好的边缘检测效果，同时，由于其引入了局部平均，使其受噪声的影响也较小。若使用较大的邻域，抗噪性会更好，但也增加了计算量，并且得到的边缘比较粗。在对精度要求不是很高的场合下，Sobel 算子是一种较为常用的边缘检测算法
索贝尔算子（Sobel operator）主要用作边缘检测，在技术上，它是一离散性差分算子，用来运算图像亮度函数的灰度之近似值。在图像的任何一点使用此算子，将会产生对应的灰度矢量或是其法矢量
Sobel卷积因子为：

该算子包含两组3x3的矩阵，分别为横向及纵向，将之与图像作平面卷积，即可分别得出横向及纵向的亮度差分近似值。如果以A代表原始图像，Gx及Gy分别代表经横向及纵向边缘检测的图像灰度值，其公式如下：

具体计算如下：

其中f(a,b), 表示图像(a,b)点的灰度值；

图像的每一个像素的横向及纵向灰度值通过以下公式结合，来计算该点灰度的大小：
通常，为了提高效率 使用不开平方的近似值：
如果梯度G大于某一阀值 则认为该点(x,y)为边缘点。
然后可用以下公式计算梯度方向：

Sobel算子根据像素点上下、左右邻点灰度加权差，在边缘处达到极值这一现象检测边缘。对噪声具有平滑作用，提供较为精确的边缘方向信息，边缘定位精度不够高。当对精度要求不是很高时，是一种较为常用的边缘检测方法。
　
——————————————————————————

4）Prewitt 算子

同 Sobel 算子相似，Prewitt 算子也是一种将方向的差分运算和局部平均相结合的方法，也是取水平和垂直两个卷积核来分别对图像中各个像素点做卷积运算，所不同的是，Sobel 算子是先做加权平均然后再微分，Prewitt 算子是先平均后求微分，其对应的卷积模版为：

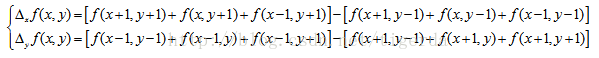
图像算法 - 常用边缘检测算法对比分析 - dingmz_frc - dingmz_frc的博客
图像中的每个像素点和以上水平和垂直两个卷积算子做卷积运算后，再计算得到
梯度幅值 G ( x,y)，然后选取适当的阈值τ ，若 G ( x,y)>τ，则 (i ,j)为边缘点，否则，判断 (i ,j)为非边缘点。由此得到一个二值图像 { g (i,j)}，即边缘图像。
在此基础上，有人提出了改进的Prewitt算子，将其扩展到八个方向，依次用这些边缘模板去检测图像，与被检测区域最为相似的样板给出最大值。用这个最大值作为算子的输出值 P[ i ,j],这样就可将边缘像素检测出来。八个方向的 Prewitt 算子模板及其所对应的边缘方向如下所示：

Prewitt 算子通过对图像上的每个像素点的八方向邻域的灰度加权差之和来进行检测边缘，对噪声有一定抑制作用，抗噪性较好，但由于采用了局部灰度平均，因此容易检测出伪边缘，并且边缘定位精度较低。

普利维特算子(Prewitt operate)：

其他计算 和sobel差不多；

Prewitt算子利用像素点上下、左右邻点灰度差，在边缘处达到极值检测边缘。对噪声具有平滑作用，定位精度不够高。

罗伯茨交叉边缘检测（Roberts Cross operator）

卷积因子如下：

灰度公式为：

近似公式为：

具体计算如下：

G(x,y)=abs(f(x,y)-f(x+1,y+1))+abs(f(x,y+1)-f(x+1,y))

灰度方向 计算公式为：

——————————————————————
5）Kirsch 算子
Kirsch 算子是一种 3×3 的非线性方向算子。其基本思想是希望改进取平均值的过程，从而尽量使边缘两侧的像素各自与自己同类的像素取平均值，然后再求平均值之差，来减小由于取平均值所造成的边缘细节丢失。通常采用八方向 Kirsch 模板的方法进行检测，取其中最大的值作为边缘强度，而将与之对应的方向作为边缘方向。常用的八方向 Kirsch 模板如下所示：
图像算法 - 常用边缘检测算法对比分析 - dingmz_frc - dingmz_frc的博客
实际的应用中，通常都是利用简单的卷积核来计算方向差分的，不同的算子对应着不同的卷积核。它们在图像的像素点上所产生的两个方向的偏导数用均方值或者绝对值求和的形式来近似代替梯度幅值，然后选取一个合适的阈值，用所得到的梯度幅值和所设定的阈值进行比较来判断边缘点。若大于所取的阈值，则判断为边缘点；否则，判断为非边缘点。很显然，在提取边缘的过程中，阈值的选取特别重要，尤其在含噪图像中，阈值的选择要折衷考虑噪声造成的伪边缘和有效边缘的丢失。
6）Laplace 算子
拉普拉斯算子是不依赖于边缘方向的二阶导数算子，它是一个标量而不是向
量，具有旋转不变即各向同性的性质。若只关心边缘点的位置而不需要了解一其周围的实际灰度差时，一般选择该算子提取图像的边缘。Laplace算子的定义为：
图像算法 - 常用边缘检测算法对比分析 - dingmz_frc - dingmz_frc的博客
用差分方程近似二阶偏倒数的结果如下:

图像算法 - 常用边缘检测算法对比分析 - dingmz_frc - dingmz_frc的博客
将这两个式子合并，可以得到近似Laplace算子的模版：
图像算法 - 常用边缘检测算法对比分析 - dingmz_frc - dingmz_frc的博客
当Laplace算子输出出现过零点时就表明有边缘存在，其中忽略无意义的过零点(均匀零区)。原则上，过零点的位置精度可以通过线性内插方法精确到子像素分辨率。但是拉普拉斯算子在图像边缘检测中并不常用。主要原因有：任何包含有二阶导数的算子比只包含有一阶导数的算子更易受噪声的影响，一阶导数很小的局部峰值也能导致二阶导数过零点，所以Laplace算子对噪声具有无法接受的敏感性； Laplace算子的幅值产生双边元，这是复杂的分割不希望有的结果;最后，Laplace算子不能检测边缘的方向。为了避免噪声的影响，必须采用特别有效的滤波方法。所以，人们提出了改进的功LOG算子。
7）LOG算子（高斯拉普拉斯算子）
LOG算子基本思想是：先在一定的范围内做平滑滤波，然后再利用差分算子来检测在相应尺度上的边缘。滤波器的选择要考虑以下两个因素：其一是滤波器在空间上要求平稳，即要求空间位置误差 Δ x要小；其二是平滑滤波器本身要求是带通滤波器，并且在有限的带通内是平稳的，即要求频域误差 Δω 要小。根据信号处理中的测不准原理， Δx 和 Δ ω是相互矛盾的，而达到测不准下限的滤波器就是高斯滤波器。Marr 和 Hildreth 提出的这种差分算子是各向同性的拉普拉斯二阶差分算子。该边缘检测器的基本特征是：
（1） 所用的平滑滤波器是高斯滤波器
（2） 增强步骤采用的是二阶导数（即二维拉普拉斯函数）
（3） 边缘检测的判据是二阶导数过零点并且对应一阶导数的极大值
该方法的特点是先用高斯滤波器与图像进行卷积，既平滑了图像又降低了噪声，使孤立的噪声点和较小的结构组织被滤除。然而由于对图像的平滑会导致边缘的延展，因此只考虑那些具有局部梯度极大值的点作为边缘点，这可以用二阶导数的零交叉来实现。拉普拉斯函数可用作二维二阶导数的近似，因为它是一种标量算子。为了避免检测出非显著的边缘，所以应该选择一阶导数大于某一阈值的零交叉点来作为边缘点。实际应用中，常用的LOG算子的模版为：
图像算法 - 常用边缘检测算法对比分析 - dingmz_frc - dingmz_frc的博客
说明: 高斯平滑运算不但可以滤除噪声，还会导致图像中的边缘和其它尖锐不连续部分模糊，而模糊程度取决于空间尺度因子σ 的大小。σ 越大，高斯滤波对噪声的滤除效果越好，但同时也会丢失重要的边缘信息，影响到边缘检测器的性能。如果σ 较小，又可能导致平滑作用不完全而留有较多的噪声。因此在实际应用中，要根据情况选择适当的σ。
8） Canny算子
1986年，Canny从边缘检测算子应该满足的三个准则出发，推导出了最优边
缘检测算子Canny算子，该算子是目前理论上相对最完善的一种边缘检测算法。
Canny提出的评价边缘检测性能优劣的三个准则分别是:
（1）好的信噪比准则。即将非边缘点判为边缘点的概率要低，将边缘点判为非边缘点的概率要低;
（2）好的定位性能准则。即检测出的边缘点要尽可能在实际边缘的中心;
（3）单边缘响应准则。即单一边缘具有唯一响应，单一边缘产生的多个响
应的概率要低，并且对虚假边缘的响应应得到最大抑制。
利用Canny算子检测边缘的土体算法如下:
（1）用式所示的高斯函数h®对图像进行平滑滤波，去除图像中的噪声。
（2）在每一点计算出局部梯度和边缘方向，可以利用Sobel算子、Roberts算子等来计算。边缘点定义为梯度方向上其强度局部最大的点。
（3）对梯度进行“非极大值抑制”。在第二步中确定的边缘点会导致梯度幅度图像中出现脊。然后用算法追踪所有脊的顶部，并将所有不在脊的顶部的像素设为零，以便在输出中给出一条细线。
（4）双阐值化和边缘连接。脊像素使用两个闽值Tl和竹做阂值处理，其中Tl Canny算子也存在不足之处:
（1）为了得到较好的边缘检测结果，它通常需要使用较大的滤波尺度，这样容易丢失一些细节
（2）Canny算子的双阈值要人为的选取，不能够自适应

实验与结果分析
实验在MATLAB R2007a平台下进行，实验的结果如下图所示：
图像算法 - 常用边缘检测算法对比分析 - dingmz_frc - dingmz_frc的博客
图像算法 - 常用边缘检测算法对比分析 - dingmz_frc - dingmz_frc的博客

其他博文参照：http://wenku.baidu.com/view/ce3aa547be1e650e52ea9945.html
http://wenku.baidu.com/view/d521aee9172ded630b1cb6ed.html

数字图像处理

几种边缘检测算子的比较

边缘检测是图像处理和计算机视觉中的基本问题，边缘检测的目的是标识数字图像中亮度变化明显的点。图像属性中的显著变化通常反映了属性的重要事件和变化。这些包括：深度上的不连续、表面方向不连续、物质属性变化和场景照明变化。边缘检测是图像处理和计算机视觉中，尤其是特征提取中的一个研究领域。图像边缘检测大幅度地减少了数据量，并且剔除了可以认为不相关的信息，保留了图像重要的结构属性。有许多方法用于边缘检测，它们的绝大部分可以划分为两类：基于查找一类和基于零穿越的一类。基于查找的方法通过寻找图像一阶导数中的最大和最小值来检测边界，通常是将边界定位在梯度最大的方向。基于零穿越的方法通过寻找图像二阶导数零穿越来寻找边界，通常是Laplacian过零点或者非线性差分表示的过零点。

人类视觉系统认识目标的过程分为两步:首先，把图像边缘与背景分离出来;然后，才能知觉到图像的细节，辨认出图像的轮廓。计算机视觉正是模仿人类视觉的这个过程。因此在检测物体边缘时，先对其轮廓点进行粗略检测，然后通过链接规则把原来检测到的轮廓点连接起来，同时也检测和连接遗漏的边界点及去除虚假的边界点。图像的边缘是图像的重要特征，是计算机视觉、模式识别等的基础，因此边缘检测是图象处理中一个重要的环节。然而，边缘检测又是图象处理中的一个难题，由于实际景物图像的边缘往往是各种类型的边缘及它们模糊化后结果的组合，且实际图像信号存在着噪声。噪声和边缘都属于高频信号，很难用频带做取舍。

这就需要边缘检测来进行解决的问题了。边缘检测的基本方法有很多，一阶的有Roberts Cross算子，Prewitt算子，Sobel算子，Canny算子， Krisch算子，罗盘算子；而二阶的还有Marr-Hildreth，在梯度方向的二阶导数过零点。现在就来简单介绍一下各种算子的算法

1.1 Roberts算子
Roberts算子是一种利用局部差分算子寻找边缘的算子，它有下式给出：

x,y)=

其中、、 分别为4领域的坐标，且是具有整数像素坐标的输人图像;其中的平方根运算使得该处理类似于人类视觉系统中发生的过程。

  Roberts算子是2X2算子模板。图1所示的2个卷积核形成了Roberts算子。图象中的每一个点都用这2个核做卷积。

1

0

0

-1

0

1

-1

0

图1 Roberts算子

1.2 Sobel算子

  Sobel算子是一种一阶微分算子，它利用像素邻近区域的梯度值来计算1个像素的梯度，然后根据一定的绝对值来取舍。它由下式给出:

Sobel算子是3*3算子模板。图2所示的2个卷积核dx 、 dy形成Sobel算子。一个核对通常的垂直边缘响应最大，而另一个核对水平边缘响应最大。2个卷积的最大值作为该点的输出值。运算结果是一幅边缘幅度图像。

图2 Sobel算子

 Prewitt算子

 Prewitt算子由下式给出：

Prewitt算子是3*3算子模板。图3所示的2个卷积核dx ,dy.形成了Prewitt算子。与Sobel算子的方法一样，图像中的每个点都用这2个核进行卷积，取最大值作为输出值。Prewitt算子也产生一幅边缘幅度图像。

1.3 Canny算子

 Canny算子是是一阶算子。其方法的实质是用1个准高斯函数作平滑运算fs=f(x,y)*G(x,y),然后以带方向的一阶微分算子定位导数最大值。

 平滑后fs(x，y)的梯度可以使用2*2的一阶有限差分近似式:

P[i,j]≈(fs[i,j+1]-fs[i,j]+fs[i+1,j+1]-fs[i+1,j])/2

Q[i,j] ≈(fs[i,j]-fs[i+1,j]+fs[i,j+1]-fs[i+1,j+1])/2

在这个2x2正方形内求有限差分的均值，便于在图像中的同一点计算二和y的偏导数梯度。幅值和方向角可用直角坐标到极坐标的坐标转化来计算:

M[i,j]=

M[i,j]反映了图象的边缘强度;反映了边缘的方向。使得M}i,j}取得局部最大值的方向角，就反映了边缘的方向。

Canny算子也可用高斯函数的梯度来近似，在理论上很接近4个指数函数的线性组合形成的最佳边缘算子。在实际工作应用中编程较为复杂且运算较慢。

2.1 LOG滤波器
LOG滤波器又称Marr-Hildreth模板或算子

=

式中：G(x,y)是对图像进行处理时选用的平滑函数(Gaussian函数);x，y为整数坐标; σ为高斯分布的均方差。对平滑后的图像fs(fs=f(x,y)*G(x,y))做拉普拉斯变换，得：

h(x,y)=G(x,y)

即先对图象平滑，后拉氏变换求二阶微分，等效于把拉氏变化作用于平滑函数，得到1个兼有平滑和二阶微分作用的模板，再与原来的图像进行卷积。用Marr-Hildreth模板与图像进行卷积的优点在于，模板可以预先算出，实际计算可以只进行卷积。

LOG滤波器有以下特点:

(1)通过图象平滑，消除了一切尺度小于σ的图像强度变化;

(2)若用其它微分法，需要计算不同方向的微分，而它无方向性，因此可以节省计算量;

(3)它定位精度高，边缘连续性好，可以提取对比度较弱的边缘点。

LOG滤波器也有它的缺点:当边缘的宽度小于算子宽度时，由于过零点的斜坡融合将会丢失细节。

LOG滤波器有无限长的拖尾，若取得很大尺寸，将使得计算不堪重负。但随着:r=的增加，LOG滤波器幅值迅速下降，当r大于一定程度时，可以忽略模板的作用，这就为节省计算量创造了条件。实际计算时，常常取n* n大小的LOG滤波器，近似n=3σ。另外，LOG滤波器可以近似为两个指数函数之差，即DOG ( Difference Of two Gaussians functions):

DOG（σ1，σ2）=-

 当σ1/σ2=1.6时，DOG代替LOG减少了计算量。

非极大值抑制（Non-Maximum Suppression，NMS）

非极大值抑制（Non-Maximum Suppression，NMS），顾名思义就是抑制不是极大值的元素，可以理解为局部最大搜索。这个局部代表的是一个邻域，邻域有两个参数可变，一是邻域的维数，二是邻域的大小。这里不讨论通用的NMS算法(参考论文《Efficient Non-Maximum Suppression》对1维和2维数据的NMS实现)，而是用于目标检测中提取分数最高的窗口的。例如在行人检测中，滑动窗口经提取特征，经分类器分类识别后，每个窗口都会得到一个分数。但是滑动窗口会导致很多窗口与其他窗口存在包含或者大部分交叉的情况。这时就需要用到NMS来选取那些邻域里分数最高（是行人的概率最大），并且抑制那些分数低的窗口。
NMS在计算机视觉领域有着非常重要的应用，如视频目标跟踪、数据挖掘、3D重建、目标识别以及纹理分析等。
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
原文: https://www.cnblogs.com/makefile/p/nms.html © 康行天下

几种算子的比较

Robert算子定位比较精确，但由于不包括平滑，所以对于噪声比较敏感。

Prewitt算子和Sobel算子都是一阶的微分算子，而前者是平均滤波，后者是加权平均滤波且检测的图像边缘可能大于2个像素。这两者对灰度渐变低噪声的图像有较好的检测效果，但是对于混合多复杂噪声的图像，处理效果就不理想了。

LOG滤波器方法通过检测二阶导数过零点来判断边缘点。LOG滤波器中的a正比于低通滤波器的宽度，a越大，平滑作用越显著，去除噪声越好，但图像的细节也损失越大，边缘精度也就越低。所以在边缘定位精度和消除噪声级间存在着矛盾，应该根据具体问题对噪声水平和边缘点定位精度要求适当选取。

讨论和比较了几种常用的边缘检测算子。梯度算子计算简单,但精度不高,只能检测出图像大致的轮廓,而对于比较细的边缘可能会忽略。Prewitt 和Sobel 算子比Roberts 效果要好一些。LOG 滤波器和Canny 算子的检测效果优于梯度算子,能够检测出图像较细的边缘部分。不同的系统,针对不同的环境条件和要求,选择合适的算子来对图像进行边缘检测。