(NIPS 2017) PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space

Abstract

很少有先前的工作研究点集的深度学习。 PointNet[20]是这个方向的先驱。然而，根据设计，PointNet并没有捕捉到由点所处的度量空间引起的局部结构，限制了其识别细粒度模式的能力和对复杂场景的通用性。在这项工作中，我们引入了一个分层神经网络，在输入点集的嵌套分区上递归地应用PointNet。通过利用度量空间距离，我们的网络能够学习具有不断增加的上下文尺度的局部特征。随着进一步观察到点集通常以变化的密度采样，这导致在均匀密度上训练的网络的性能大大降低，我们提出了新的集合学习层来自适应地组合来自多个尺度的特征。实验表明，我们的网络PointNet++能够高效、鲁棒地学习深度点集特征。特别是，在具有挑战性的3D点云基准测试中，已经获得了明显优于最先进水平的结果。

1 Introduction

我们对分析几何点集感兴趣，这些点集是欧几里得空间中点的集合。一种特别重要的几何点集类型是由3D扫描仪捕获的点云，例如，来自适当配备的自动驾驶汽车。作为一个集合，这些数据必须对其成员的排列保持不变。此外，距离度量定义了可能表现出不同属性的局部邻域。例如，点的密度和其他属性在不同位置可能不均匀——在3D扫描中，密度变化可能来自透视效果、径向密度变化、运动等。

很少有先前的工作研究点集的深度学习。PointNet[20]是直接处理点集的开创性工作。PointNet的基本思想是学习每个点的空间编码，然后将所有单独的点要素聚合为一个全局点云特征。按照它的设计，PointNet不会捕获由度量引起的局部结构。然而，事实证明，利用局部结构对于卷积架构的成功很重要。CNN将规则网格上定义的数据作为输入，能够沿着多分辨率层次结构以越来越大的比例逐步捕捉特征。在较低水平，神经元的感受野较小，而在较高水平，神经元的感受野较大。沿层次结构抽象局部模式的能力可以更好地推广到未见过的情况。

我们引入了一个名为PointNet++的分层神经网络，以分层方式处理在度量空间中采样的一组点。PointNet++的总体思路很简单。我们首先通过underlying space的距离度量将点集划分为重叠的局部区域。类似于CNN，我们从小邻域中提取捕捉精细几何结构的局部特征；与CNN类似，我们从小邻域中提取捕获精细几何结构的局部特征；这些局部特征被进一步分组为更大的单元并进行处理以产生更高级别的特征。重复这个过程，直到我们获得整个点集的特征。PointNet++的设计必须解决两个问题：如何产生点集的分区，以及如何通过局部特征学习器抽象出点集或局部特征。

PointNet++的设计必须解决两个问题：如何产生点集的分区，以及如何通过局部特征学习器抽象出点集或局部特征。这两个问题是相互关联的，因为点集的分区必须产生跨分区的共同结构，所以局部特征学习器的权重可以共享，就像在卷积设置中一样。我们选择的本地特征学习器是PointNet。正如该工作中所证明的，PointNet是一个有效的架构，可以处理无序的点集，以进行语义特征提取。此外，这个架构对输入数据的损坏也很稳定。作为一个基本构件，PointNet将局部点或特征集抽象为更高层次的表示。在这种观点下，PointNet++在输入集的嵌套分区上递归地应用PointNet。

仍然存在的一个问题是如何生成点集的重叠分区。每个分区被定义为底层欧几里得空间中的一个邻域球，其参数包括质心位置和尺度。为了均匀地覆盖整个集合，通过最远点采样（FPS）算法在输入点集合中选择质心。与以固定步幅扫描空间的体积CNN相比，我们的局部感受野依赖于输入数据和度量，因此更有效率。

然而，由于特征尺度的纠缠性和输入点集的非均匀性，确定合适的局部邻域球的尺度是一个更具挑战性但更有趣的问题。我们假设输入点集在不同区域可能具有可变密度，这在结构传感器扫描等实际数据中很常见[18]（见图1）。因此，我们的输入点集与 CNN 输入非常不同，CNN 输入可以看作是在具有均匀恒定密度的规则网格上定义的数据。在CNN中，与局部分区规模相对应的是内核的大小。[25]表明使用较小的内核有助于提高CNN的能力。然而，我们对点集数据的实验为这一规则提供了相反的证据。由于采样不足，小邻域可能由太少的点组成，这可能不足以允许PointNets稳健地捕获模式。

图1：从结构传感器捕获的扫描可视化（左：RGB；右：点云）

我们论文的一个重要贡献是PointNet++在多个尺度上利用邻域来实现鲁棒性和细节捕捉。在训练期间，在随机输入dropout的辅助下，该网络学会了自适应加权在不同尺度上检测到的模式，并根据输入数据结合多尺度特征。实验表明，我们的PointNet++能够高效、稳定地处理点集。特别是，在具有挑战性的3D点云基准测试中，获得了明显优于最先进水平的结果。

2 Problem Statement

假设$\mathcal{X}=(M,d)$是一个离散的度量空间，它的度量是从欧几里得空间${\mathbb{R}}^n$继承而来的，其中$M\subseteq {\mathbb{R}}^n$是点集，$d$是距离度量。此外，周围欧几里得空间中$M$的密度可能并非处处均匀。我们对学习集合函数$f$感兴趣，集合函数$f$将$\mathcal{X}$作为输入(以及每个点的附加特征),并产生对$\mathcal{X}$进行重新分级的语义信息。在实践中，这样的$f$可以是为$\mathcal{X}$分配标签的分类函数，也可以是为$M$的每个成员分配每个点标签的分割函数。

3 Method

我们的工作可以看作是PointNet[20]的扩展，增加了层次结构。我们首先回顾PointNet（第3.1节），然后介绍具有层次结构的PointNet的基本扩展（第3.2节）。最后，我们提出了我们的 PointNet++，即使在非均匀采样的点集中也能稳健地学习特征（第3.3节）。

3.1 Review of PointNet [20]: A Universal Continuous Set Function Approximator

给定一个具有$x_i\in {\mathbb{R}}^d$的无序点集$\left\{x_1,x_2,\dots ,x_n\right\}$，可以定义一个集合函数$f:\mathcal{X}\to \mathbb{R}$将一组点映射到一个向量：
$$f\left(x_1,x_2,\dots ,x_n\right)=\gamma \left(\underset{i=1,\dots ,n}{\mathrm{MAX}}\left\{h\left(x_i\right)\right\}\right)\text{\hspace{1em}(1)}$$
其中$\gamma$和$h$通常是多层感知器 (MLP) 网络。

公式(1)中的集合函数$f$对输入点排列是不变的，并且可以任意近似任何连续集合函数[20]。请注意，$h$的响应可以解释为一个点的空间编码（详见[20]）。

PointNet在一些基准测试中取得了令人印象深刻的表现。然而，它缺乏捕捉不同尺度的局部环境的能力。我们将在下一节介绍分层特征学习框架来解决这个限制。

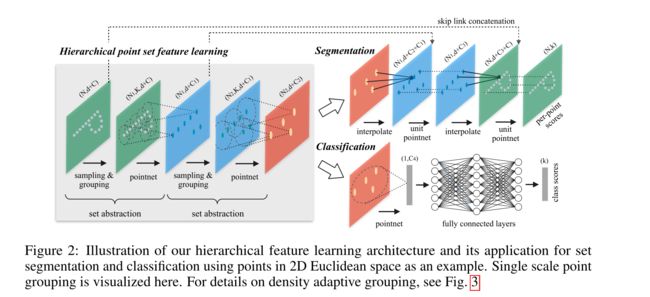
图2：以2D欧几里得空间中的点为例，说明我们的分层特征学习架构及其在集合分割和分类中的应用。单尺度点分组在这里可视化。有关密度自适应分组的详细信息，请参见图3

3.2 Hierarchical Point Set Feature Learning

虽然PointNet使用单个最大池化操作来聚合整个点集，但我们的新架构构建了点的分层分组，并沿层次逐步抽象出越来越大的局部区域。我们的层次结构由许多集合的抽象级别组成（图2）。在每个级别，一组点被处理和抽象，以产生一个具有更少元素的新集合。集合抽象层由三个关键层组成：Sampling层、Grouping层和PointNet层。Sampling层从输入点中选择一组点，这些点定义了局部区域的质心。然后，Grouping层通过在质心周围寻找“相邻”点来构造局部区域集。PointNet层使用mini-PointNet将局部区域模式编码为特征向量。

一组抽象级别将$N\times (d+C)$矩阵作为输入，该矩阵来自具有$d-dim$坐标和$C-dim$点特征的$N$个点。它输出$N^{\prime }$个子采样点的$N^{\prime }\times \left(d+C^{\prime }\right)$矩阵，该矩阵具有$d-dim$坐标和概括局部上下文的新$C^{\prime }-\dim$特征向量。我们将在以下段落中介绍一组抽象级别的层。

Sampling层 给定输入点$\left\{x_1,x_2,\dots ,x_n\right\}$，我们使用迭代最远点采样 (FPS) 来选择点$\left\{x_{i_1},x_{i_2},\dots ,x_{i_m}\right\}$的子集，使得 $x_{i_j}$ 是最远点（以度量距离）从集合 $\left\{x_{i_1},x_{i_2},\dots ,x_{i_{j-1}}\right\}$关于其余点。使得$x_{i_j}$是与集合$\left\{x_{i_1},x_{i_2},\dots ,x_{i_{j-1}}\right\}$相对于其余点最远的点（以度量距离计）。与随机抽样相比，在相同数量的质心的情况下，它对整个点集的覆盖率更高。与扫描与数据分布无关的向量空间的 CNN 相比，我们的采样策略以数据相关的方式生成感受野。

Grouping层 该层的输入是一个大小为$N\times (d+C)$的点集和一组大小为$N^{\prime }\times d$的质心的坐标。输出是大小为$N^{\prime }\times K\times (d+C)$的点集组，其中每个组对应于一个局部区域，$K$是质心点附近的点数。请注意，$K$因组而异，但随后的PointNet层能够将灵活数量的点转换为固定长度的局部区域特征向量。在卷积神经网络中，像素的局部区域由阵列索引在像素的某个曼哈顿距离（内核大小）内的像素组成。在从度量空间采样的点集中，点的邻域由度量距离定义。

Ball query查找查询点半径范围内的所有点（实现时设置上限为$K$）。另一种范围查询是$K$最近邻 (kNN) 搜索，它找到固定数量的相邻点。与kNN相比，ball query的局部邻域保证了固定的区域尺度，从而使局部区域特征在空间上更具泛化性，这对于需要局部模式识别的任务（例如语义点标记）是首选。

PointNet层 在这一层中，输入是$N^{\prime }$个点的局部区域，数据大小为$N^{\prime }\times K\times (d+C)$。输出中的每个局部区域都由其质心和编码质心邻域的局部特征抽象。输出数据大小为$N^{\prime }\times \left(d+C^{\prime }\right)$。

局部区域中的点的坐标首先被转换到相对于质心点的局部坐标系中:$x_i^{(j)}=x_i^{(j)}-{\hat{x}}^{(j)}$用于$i=1,2,\dots ,K$和$j=1,2,\dots ,d$，其中$\hat{x}$是质心的坐标。我们使用Sec.3.1中描述的PointNet[20]作为局部模式学习的基本构建块。通过使用相对坐标和点特征，我们可以捕获局部区域中的点对点关系。

3.3 非均匀采样密度下的鲁棒特征学习

如前所述，点集在不同区域具有不均匀的密度是很常见的。这种不均匀性给点集特征学习带来了重大挑战。在密集数据中学习的特征可能无法推广到稀疏采样的区域。因此，为稀疏点云训练的模型可能无法识别细粒度的局部结构。

理想情况下，我们希望尽可能仔细地检查点集，以捕获密集采样区域中最精细的细节。然而，在低密度区域禁止这种近距离检查，因为局部模式可能会因抽样不足而受到破坏。在这种情况下，我们应该在更近的地方寻找更大规模的模式。为了实现这一目标，我们提出了密度自适应PointNet层（图3），当输入采样密度发生变化时，它学习组合来自不同尺度区域的特征。我们将具有密度自适应PointNet层的分层网络称为PointNet++。

之前在第3.2节中，每个抽象层次都包含单个尺度的分组和特征提取。在PointNet++中，每个抽象层次提取多个尺度的局部模式，并根据局部点密度进行智能组合。在对局部区域进行分组和组合不同尺度的特征方面，我们提出了两种类型的密度自适应层，如下所示。

图3:（a）多尺度分组（MSG）；(b) 多分辨率分组(MRG)。

多尺度分组（MSG） 如图3(a)所示，捕获多尺度模式的一种简单但有效的方法是应用具有不同尺度的分组层，然后根据PointNets提取每个尺度的特征。将不同尺度的特征串联起来形成多尺度特征。

我们训练网络学习优化策略以结合多尺度特征。这是通过随机丢弃每个实例的随机概率的输入点来完成的，我们称之为random input dropout。具体来说，对于每个训练点集，我们选择从$[0，p]$均匀采样的丢失率$\theta$，其中$p\le 1$。对于每个点，我们随机丢弃一个概率为$\theta$的点。实际上，我们设置$p=0.95$，以避免产生空点集。在这样做的过程中，我们为网络提供了各种稀疏度(由$\theta$引起)和变化均匀性(由dropout的随机性引起)的训练集。在测试期间，我们保留所有可用的点。

多分辨率分组(MRG) 上面的MSG方法计算量很大，因为它在每个质心点的大规模邻域上运行局部PointNet。特别地，由于质心点的数量通常在最低层相当大，所以时间成本很大。在这里，我们提出了一种替代方法，可以避免这种昂贵的计算，但仍然保留根据点的分布特性自适应聚合信息的能力。在图3(b)中，在某个级别$L_i$的区域的特征是两个向量的连接。一个向量(图中左侧)是通过使用集合抽象级别从较低级别$L_{i-1}$汇总每个子区域的特征而获得的。另一个向量（右）是使用单个PointNet直接处理局部区域中的所有原始点获得的特征。当局部区域的密度较低时，第一个向量可能不如第二个向量可靠，因为计算第一个向量的子区域包含更稀疏的点并且更容易受到采样不足的影响。在这种情况下，第二个向量的权重应该更高。另一方面，当局部区域的密度很高时，第一个向量提供更精细的信息，因为它具有在较低级别递归地检查更高分辨率的能力。

与MSG相比，该方法的计算效率更高，因为我们避免了在最低级别的大规模邻域中进行特征提取。

3.4 Point Feature Propagation for Set Segmentation

在集合抽象层，对原始点集进行二次采样。然而，在语义点标注等集合分割任务中，我们希望获得所有原始点的点特征。一种解决方案是总是在所有集合抽象层中采样所有点作为质心，然而这导致高计算成本。另一种方法是将特征从二次采样点传播到原始点。

我们采用基于距离的插值和跨级跳跃链接的分层传播策略（如图2所示）。在特征传播级别中，我们将点特征从$N_l\times (d+C)$点传播到$N_{l-1}$点，其中$N_{l-1}$和$N_l$($N_l\le N_{l-1}$)是集合抽象级别$l$的输入和输出的点集大小。我们通过在$N_{l-1}$点的坐标处内插$N_l$点的特征值$f$来实现特征传播。在插值的多种选择中，我们使用基于$k$个最近邻的反距离加权平均(如公式(2)，默认情况下我们使用$p=2，k=3$)。然后，$N_{l-1}$点上的插值要素与集合抽象级别中的跳跃链接点要素连接在一起。然后连接的特征通过一个”unit pointnet“，类似于CNN中的一对一卷积。应用一些共享的全连接层和ReLU层来更新每个点的特征向量。重复该过程，直到我们将特征传播到原始点集。
$$f^{(j)}(x)=\frac{{\sum }_{i=1}^k{w}_i(x)f_i^{(j)}}{{\sum }_{i=1}^k{w}_i(x)}\text{ 其中 }{w}_i(x)=\frac{1}{d{\left(x,x_i\right)}^p},j=1,\dots ,C\text{\hspace{1em}(2)}$$

4 Experiments

数据集 我们评估了四个数据集，从2D目标（MNIST[11]）、3D目标（ModelNet40[31]刚体目标、SHREC15 [12]非刚体目标）到真实的3D场景（ScanNet[5]）。目标分类通过准确性进行评估。语义场景标记通过[5]之后的平均体素分类精度进行评估。我们在下面列出了每个数据集的实验设置：

• MNIST：具有60k训练和10k测试样本的手写数字图像。
• ModelNet40：40个类别的CAD模型（大部分是人造的）。我们使用官方拆分，其中9,843个形状用于训练，2,468 个用于测试。
• SHREC15:来自50个类别的1200个形状。每个类别包含24个形状，其中大部分是具有各种姿势的有机形状，如马、猫等。我们使用五重交叉验证来获得该数据集上的分类准确性。
• ScanNet: 1513扫描重建的室内场景。我们遵循[5]中的实验设置，使用1201个场景进行训练，312个场景进行测试。

4.1 Point Set Classification in Euclidean Metric Space

我们在分类从2D(MNIST)和3D(ModlNet40)欧式空间采样的点云上评估我们的网络。MNIST图像被转换成数字像素位置的2D点云。3D点云是从ModelNet40形状的网格曲面中采样的。默认情况下，我们为MNIST使用512个点，为ModelNet40使用1024个点。在表2的最后一行(我们的法线),我们使用面法线作为额外的点特征，这里我们也使用更多的点(N = 5000)来进一步提高性能。所有的点集都被标准化为零均值，并且在一个单位球内。我们使用一个具有三个完全连接层的三级分层网络。（有关网络架构和实验准备的更多详细信息，请参见附录。）

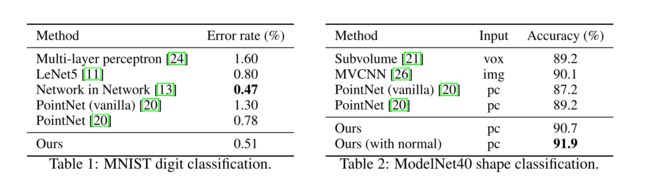
结果 在表1和表2中，我们将我们的方法与一组具有代表性的现有技术进行比较。请注意，表2中的PointNet(vanilla)是[20]中不使用转换网络的版本，相当于我们只有一层的分层网络。

首先，我们的分层学习架构比非分层PointNet[20]实现了显着更好的性能。在MNIST中，我们看到从PointNet（vanilla）和PointNet到我们的方法，错误率相对减少了60.8%和34.6%。在ModelNet40分类中，我们还看到使用相同的输入数据大小（1024 个点）和特征（仅坐标），我们的比PointNet强得多。其次，我们观察到基于点集的方法甚至可以实现与成熟图像CNN更好或相似的性能。在 MNIST 中，我们的方法（基于 2D 点集）实现了接近Network in Network CNN的精度。在ModelNet40中，我们的正常信息显着优于之前最先进的方法MVCNN[26]。

对采样密度变化的鲁棒性 直接从现实世界中捕获的传感器数据通常存在严重的不规则采样问题（图1）。我们的方法选择多个尺度的点邻域，并通过适当加权来学习平衡描述性和鲁棒性。

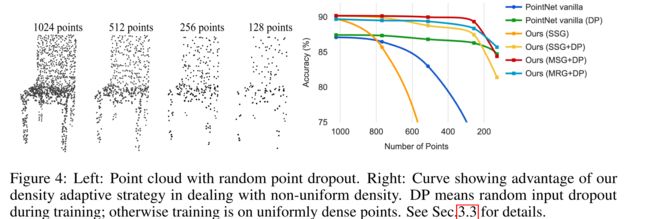
图4:左:random point dropout的点云。右图:曲线显示了我们的密度自适应策略在处理不均匀密度方面的优势。DP表示训练过程中的随机输入丢失；否则训练是在均匀密集的点上进行的。详见第3.3节。

我们在测试期间随机丢弃点(见左图4 ),以验证我们的网络对不均匀和稀疏数据的鲁棒性。在图4右侧，我们看到MSG+DP(训练期间随机输入丢失的多尺度分组)和MRG+DP(训练期间随机输入丢失(random input dropout)的多分辨率分组)对采样密度变化非常鲁棒。从1024到256个测试点，MSG+DP性能下降不到1%。此外，与替代方案相比，它在几乎所有采样密度上都实现了最佳性能。PointNet vanilla[20]在密度变化下相当健壮，因为它关注全局抽象而不是细节。然而，与我们的方法相比，细节的损失也使得它不那么强大。SSG（在每个级别中具有单尺度分组的消融PointNet++）无法推广到稀疏采样密度，而SSG+DP通过在训练时间随机丢弃点来修正问题。

4.2 Point Set Segmentation for Semantic Scene Labeling

为了验证我们的方法适用于大规模点云分析，我们还评估了语义场景标记任务。目标是预测室内扫描点的语义目标标签。[5] 在体素化扫描上使用全卷积神经网络提供了baseline。它们完全依赖于扫描几何结构而不是RGB信息，并在每个体素的基础上报告精度。为了进行公平的比较，我们在所有实验中移除了RGB信息，并按照[5]将点云标签预测转换为体素标签。我们还与[20]进行了比较。在图5(蓝条)中，在每个体素的基础上报告了精度。

图5: Scannet标签精度。

我们的方法远远优于所有的baseline方法。与[5]相比，我们直接在点云上学习，以避免额外的量化误差，并进行与数据相关的采样，以实现更有效的学习。与[20]相比，我们的方法引入了分层特征学习，并捕获了不同尺度下的几何特征。这对于理解多个级别的场景和标记不同大小的目标非常重要。我们将示例场景标记结果显示在图6中。

图6:Scannet标签结果。[20]正确捕捉房间的整体布局，但未能发现家具。相比之下，我们的方法在分割房间布局之外的目标方面要好得多。

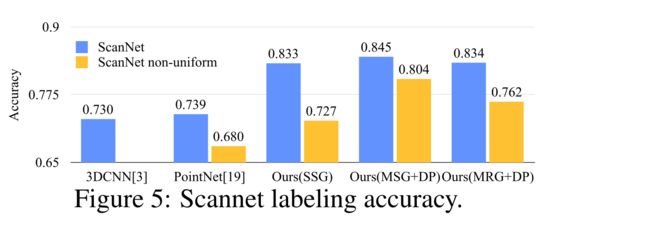
对采样密度变化的鲁棒性 为了测试我们训练的模型如何在采样密度不均匀的扫描中执行，我们合成了类似于图1中的Scannet场景的虚拟扫描，并根据这些数据评估我们的网络。我们向读者推荐有关我们如何生成虚拟扫描的补充材料。我们在三种设置（SSG、MSG+DP、MRG+DP）中评估我们的框架，并与baseline方法进行比较[20]。

性能比较如图5所示（黄色条）。我们看到，由于采样密度从均匀点云转移到虚拟扫描场景，SSG性能大大下降。另一方面，MRG网络对采样密度变化更加稳健，因为它能够在采样稀疏时自动切换到描绘更粗粒度的特征。即使在训练数据(具有随机丢失的均匀点)和具有非均匀密度的扫描数据之间存在差距，我们的MSG网络也仅受到轻微影响，并且在比较中实现了方法中的最佳精度。这些证明了我们的密度自适应层设计的有效性。

4.3 Point Set Classification in Non-Euclidean Metric Space

在这一节中，我们展示了我们的方法对非欧式空间的推广。在非刚体形状分类中(图7)，一个好的分类器应该能够正确地将图7中的(a)和©分类为相同的类别，即使给定它们在姿态上的差异，这需要内在结构的知识。SHREC15中的形状是嵌入在3D间中的2D表面。沿表面的测地线距离自然会产生一个度量空间。我们通过实验表明，在这种度量空间中采用PointNet++是一种捕捉底层(underlying)点集内在结构的有效方法。

图7:非刚体形状分类的一个例子。

对于[12]中的每个形状，我们首先构造由成对测地距离产生的度量空间。我们按照[23]获得模拟测地线距离的嵌入度量。接下来，我们提取该度量空间中的固有点特征，包括WKS[1]、HKS[27]和多尺度高斯曲率[16]。我们使用这些特征作为输入，然后根据底层(underlying)度量空间对点进行采样和分组。通过这种方式，我们的网络学会了捕捉不受形状的特定姿势影响的多尺度内在结构。替代设计选择包括使用$XYZ$坐标作为点特征，或者使用欧式空间${\mathbb{R}}^3$作为基础度量空间。我们在下面展示这些都不是最佳选择。

结果 我们在表3中将我们的方法与之前最先进的方法[14]进行了比较。[14]提取测地线矩作为形状特征，并使用堆叠稀疏自动编码器来消化这些特征以预测形状类别。我们的方法使用非欧式度量空间和内在特征，在所有设置中实现了最佳性能，并且大幅度优于[14]。

比较我们方法的第一种和第二种设置，我们看到内在特征对于非刚体形状分类非常重要。$XYZ$特征无法揭示内在结构，并且受姿势变化的影响很大。比较我们方法的第二和第三个设置，我们看到使用测地线邻域比欧式邻域更有益。欧式邻域可能包括表面上较远的点，并且当形状提供非刚体变形时，该邻域可能会显著改变。这给有效的权重共享带来了困难，因为局部结构可能变得组合复杂。另一方面，曲面上的测地线邻域则解决了这个问题，提高了学习效率。

4.4 Feature Visualization.

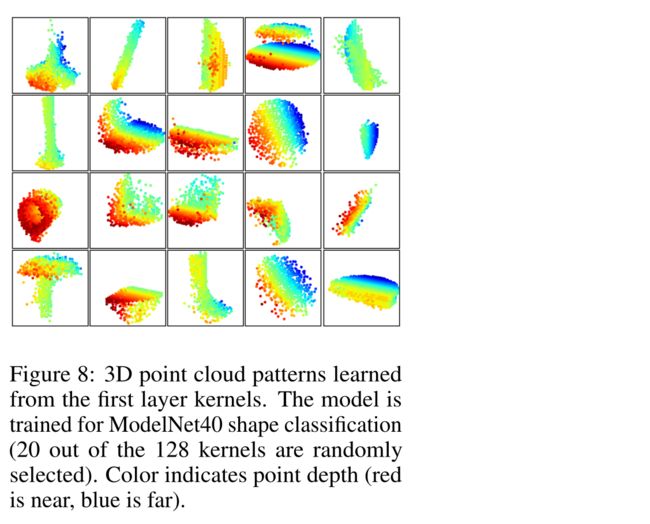
在图8中，我们可视化了我们的分级网络的第一级内核已经学习的内容。我们在空间中创建了一个体素网格，并聚集了网格单元中激活某些神经元最多的局部点集(使用了最多100个示例)。保留具有高票数的网格单元并将其转换回3D点云，这代表了神经元识别的模式。由于模型是在主要由家具组成的ModelNet40上训练的，因此我们在可视化中看到了平面、双平面、线、角等结构。

图8：从第一层内核学习的3D点云模式。该模型针对ModelNet40形状分类进行了训练（随机选择128个内核中的20个）。颜色表示点深度（红色表示近，蓝色表示远）。

5 Related Work

分层特征学习的想法非常成功。在所有学习模型中，卷积神经网络[10, 25, 8]是最突出的模型之一。然而，卷积不适用于具有距离度量的无序点集，这是我们工作的重点。

一些最近的工作[20，28]研究了如何将深度学习应用于无序集。他们忽略了底层(underlying)的距离度量，即使点集拥有一个。结果，它们无法捕获点的局部上下文，并且对全局集合转换和标准化很敏感。在这项工作中，我们针对从度量空间中采样的点，并通过在我们的设计中明确考虑潜在的距离度量来解决这些问题。

从度量空间采样的点通常是嘈杂的并且具有不均匀的采样密度。这会影响有效的点特征提取并导致学习困难。关键问题之一是为点特征设计选择合适的尺度。以前在几何处理社区或摄影测量和遥感社区中已经开发了几种方法[19,17,2,6,7,30]。与所有这些工作相比，我们的方法学习以端到端的方式提取点特征并平衡多个特征尺度。

在3D度量空间中，除了点集之外，还有几种流行的深度学习表示方法，包括体积网格[21，22，29]和几何图形[3，15，33]。然而，在这些工作中，没有一个明确地考虑了非均匀采样密度的问题。

6 Conclusion

在这项工作中，我们提出了PointNet++这种强大的神经网络架构，用于处理度量空间中采样的点集。PointNet++递归地作用于输入点集的嵌套分割，并且在学习关于距离度量的等级特征方面是有效的。为了处理非均匀点采样问题，我们提出了两个新的集合抽象层，根据局部点密度智能地聚集多尺度信息。这些贡献使我们能够在具有挑战性的3D点云基准测试中实现一流的性能。

在未来，如何通过在每个局部区域中共享更多的计算来加速我们提出的网络的推理速度是值得考虑的，特别是对于MSG和MRG层。在更高维度的度量空间中发现应用也是有趣的，其中基于CNN的方法在计算上是不可行的，而我们的方法可以很好地扩展。

References

[1] M. Aubry, U. Schlickewei, and D. Cremers. The wave kernel signature: A quantum mechanical approach to shape analysis. In Computer Vision Workshops (ICCV Workshops), 2011 IEEE International Conference on, pages 1626–1633. IEEE, 2011.

[2] D. Belton and D. D. Lichti. Classification and segmentation of terrestrial laser scanner point clouds using local variance information. Iaprs, Xxxvi, 5:44–49, 2006.

[3] J. Bruna, W. Zaremba, A. Szlam, and Y . LeCun. Spectral networks and locally connected networks on graphs. arXiv preprint arXiv:1312.6203, 2013.

[4] A. X. Chang, T. Funkhouser, L. Guibas, P . Hanrahan, Q. Huang, Z. Li, S. Savarese, M. Savva, S. Song, H. Su, J. Xiao, L. Yi, and F. Y u. ShapeNet: An Information-Rich 3D Model Repository. Technical Report arXiv:1512.03012 [cs.GR], 2015.

[5] A. Dai, A. X. Chang, M. Savva, M. Halber, T. Funkhouser, and M. Nießner. Scannet: Richly-annotated 3d reconstructions of indoor scenes. arXiv preprint arXiv:1702.04405, 2017.

[6] J. Demantké, C. Mallet, N. David, and B. V allet. Dimensionality based scale selection in 3d lidar point clouds. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 38(Part 5):W12, 2011.

[7] A. Gressin, C. Mallet, J. Demantké, and N. David. Towards 3d lidar point cloud registration improvement using optimal neighborhood knowledge. ISPRS journal of photogrammetry and remote sensing, 79:240– 251, 2013.

[8] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 770–778, 2016.

[9] D. Kingma and J. Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.

[10] A. Krizhevsky, I. Sutskever, and G. E. Hinton. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems, pages 1097–1105, 2012.

[11] Y . LeCun, L. Bottou, Y . Bengio, and P . Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.

[12] Z. Lian, J. Zhang, S. Choi, H. ElNaghy, J. El-Sana, T. Furuya, A. Giachetti, R. A. Guler, L. Lai, C. Li, H. Li, F. A. Limberger, R. Martin, R. U. Nakanishi, A. P . Neto, L. G. Nonato, R. Ohbuchi, K. Pevzner, D. Pickup, P . Rosin, A. Sharf, L. Sun, X. Sun, S. Tari, G. Unal, and R. C. Wilson. Non-rigid 3D Shape Retrieval. In I. Pratikakis, M. Spagnuolo, T. Theoharis, L. V . Gool, and R. V eltkamp, editors, Eurographics Workshop on 3D Object Retrieval. The Eurographics Association, 2015.

[13] M. Lin, Q. Chen, and S. Yan. Network in network. arXiv preprint arXiv:1312.4400, 2013.

[14] L. Luciano and A. B. Hamza. Deep learning with geodesic moments for 3d shape classification. Pattern Recognition Letters, 2017.

[15] J. Masci, D. Boscaini, M. Bronstein, and P . V andergheynst. Geodesic convolutional neural networks on riemannian manifolds. In Proceedings of the IEEE International Conference on Computer Vision Workshops, pages 37–45, 2015.

[16] M. Meyer, M. Desbrun, P . Schröder, A. H. Barr, et al. Discrete differential-geometry operators for triangulated 2-manifolds. Visualization and mathematics, 3(2):52–58, 2002.

[17] N. J. MITRA, A. NGUYEN, and L. GUIBAS. Estimating surface normals in noisy point cloud data. International Journal of Computational Geometry & Applications, 14(04n05):261–276, 2004.

[18] I. Occipital. Structure sensor-3d scanning, augmented reality, and more for mobile devices, 2016.

[19] M. Pauly, L. P . Kobbelt, and M. Gross. Point-based multiscale surface representation. ACM Transactions on Graphics (TOG), 25(2):177–193, 2006.

[20] C. R. Qi, H. Su, K. Mo, and L. J. Guibas. Pointnet: Deep learning on point sets for 3d classification and segmentation. arXiv preprint arXiv:1612.00593, 2016.

[21] C. R. Qi, H. Su, M. Nießner, A. Dai, M. Yan, and L. Guibas. V olumetric and multi-view cnns for object classification on 3d data. In Proc. Computer Vision and Pattern Recognition (CVPR), IEEE, 2016.

[22] G. Riegler, A. O. Ulusoys, and A. Geiger. Octnet: Learning deep 3d representations at high resolutions. arXiv preprint arXiv:1611.05009, 2016.

[23] R. M. Rustamov, Y . Lipman, and T. Funkhouser. Interior distance using barycentric coordinates. In Computer Graphics F orum, volume 28, pages 1279–1288. Wiley Online Library, 2009.

[24] P . Y . Simard, D. Steinkraus, and J. C. Platt. Best practices for convolutional neural networks applied to visual document analysis. In ICDAR, volume 3, pages 958–962, 2003.

[25] K. Simonyan and A. Zisserman. V ery deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556, 2014.

[26] H. Su, S. Maji, E. Kalogerakis, and E. G. Learned-Miller. Multi-view convolutional neural networks for 3d shape recognition. In Proc. ICCV , to appear, 2015.

[27] J. Sun, M. Ovsjanikov, and L. Guibas. A concise and provably informative multi-scale signature based on heat diffusion. In Computer graphics forum, volume 28, pages 1383–1392. Wiley Online Library, 2009.

[28] O. Vinyals, S. Bengio, and M. Kudlur. Order matters: Sequence to sequence for sets. arXiv preprint arXiv:1511.06391, 2015.

[29] P .-S. W ANG, Y . LIU, Y .-X. GUO, C.-Y . SUN, and X. TONG. O-cnn: Octree-based convolutional neural networks for 3d shape analysis. 2017.

[30] M. Weinmann, B. Jutzi, S. Hinz, and C. Mallet. Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers. ISPRS Journal of Photogrammetry and Remote Sensing, 105:286–304, 2015.

[31] Z. Wu, S. Song, A. Khosla, F. Y u, L. Zhang, X. Tang, and J. Xiao. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 1912–1920, 2015.

[32] L. Yi, V . G. Kim, D. Ceylan, I.-C. Shen, M. Yan, H. Su, C. Lu, Q. Huang, A. Sheffer, and L. Guibas. A scalable active framework for region annotation in 3d shape collections. SIGGRAPH Asia, 2016.

[33] L. Yi, H. Su, X. Guo, and L. Guibas. Syncspeccnn: Synchronized spectral cnn for 3d shape segmentation. arXiv preprint arXiv:1612.00606, 2016.

Supplementary

A 概述

这份补充材料提供了更多的实验细节，包括更多的实验来验证和分析我们提出的方法。

在第二节中，我们提供了主要论文中用于实验的特定网络架构，并且还描述了数据准备和训练的细节。在Sec C中，我们展示了更多的实验结果，包括部分分割和邻域查询分析的基准性能，对采样随机性和时空复杂度的敏感性。

B 实验中的细节

架构协议 我们使用以下符号来描述我们的网络架构。$\mathrm{SA}\left(K,r,\left[l_1,\dots ,l_d\right]\right)$是具有球半径$r$的$K$个局部区域的集合抽象$SA$级，使用宽度为$l_i(i=1,\dots ,d)$。$\mathrm{S}\mathrm{A}\left(\left[l_1,\dots l_d\right]\right)$是一个全局集合抽象层，它将集合转换成一个单独的向量。在多尺度设置中(如MSG中)，我们使用$\mathbf{S}\mathbf{A}(K,\left[r^{(1)},\dots ,r^{(m)}\right],\left[\left[l_1^{(1)},\dots ,l_d^{(1)}\right],\dots ,\left[l_1^{(m)},\dots ,l_d^{(m)}\right]\right])$来用$m$个刻度表示MSG。

$\mathrm{F}\mathrm{C}(l,dp)$表示全连接层，宽度为$l$，下降（dropout）率为$dp$。$\mathrm{FP}\left(l_1,\dots ,l_d\right)$是具有$d$个全连接层的特征传播$(FP)$层。它用于更新从插值和跳过链接(skip link)连接而来的特征。除了最后一个分数预测层外，所有全连接层之后都是批量归一化和ReLU。

B.1 网络架构

对于所有分类实验，我们使用以下具有不同$K$（类别数）的架构（我们的SSG）：
$$\begin{array}{rl}& SA(512,0.2,[64,64,128])\to SA(128,0.4,[128,128,256])\to SA([256,512,1024])\to \\ & FC(512,0.5)\to FC(256,0.5)\to FC(K)\end{array}$$
多尺度分组(MSG)网络(PointNet++)架构如下:
$SA(512,[0.1,0.2,0.4],[[32,32,64],[64,64,128],[64,96,128]])\to$
$SA(128,[0.2,0.4,0.8],[[64,64,128],[128,128,256],[128,128,256]])\to$
$SA([256,512,1024])\to FC(512,0.5)\to FC(256,0.5)\to FC(K)$

跨级多分辨率分组(MRG)网络的架构使用三个分支:

分支1：$SA(512,0.2,[64,64,128])\to SA(64,0.4,[128,128,256])$

分支2：$SA(512,0.4,[64,128,256])$使用原始点的$r=0.4$个区域

分支3: $SA(64,128,256,512)$使用所有原始点。

分支4：$SA(256,512,1024)$

分支1和分支2被连接并被输入到分支4。分支3和分支4的输出然后被连接并输入到$FC(512,0.5)\to FC(256,0.5)\to FC(K)$用于分类。

用于语义场景标记的网络(FP中最后两个完全连接的层之后是丢弃（drop）率为0.5的dropout层):
$$\begin{array}{rl}& SA(1024,0.1,[32,32,64])\to SA(256,0.2,[64,64,128])\to \\ & SA(64,0.4,[128,128,256])\to SA(16,0.8,[256,256,512])\to \\ & FP(256,256)\to FP(256,256)\to FP(256,128)\to FP(128,128,128,128,K)\end{array}$$

用于语义和部分分割的网络(FP中最后两个完全连接的层之后是丢弃率为0.5的丢弃（dropout）层):
$$\begin{array}{rl}& SA(512,0.2,[64,64,128])\to SA(128,0.4,[128,128,256])\to SA([256,512,1024])\to \\ & FP(256,256)\to FP(256,128)\to FP(128,128,128,128,K)\end{array}$$

B.2 虚拟扫描生成

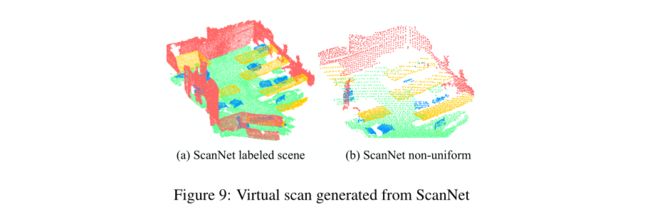
在本节中，我们将描述如何从ScanNet场景中生成具有非均匀采样密度的标记虚拟扫描。对于ScanNet中的每个场景，我们将相机位置设置在地板平面的质心上方1.5m处，并在水平面上以8个方向均匀地旋转相机方向。在每个方向上，我们使用一个大小为100像素乘75像素的图像平面，并将来自相机的光线通过每个像素投射到场景中。这提供了一种选择场景中可见点的方法。然后，我们可以为每个类似的测试场景生成8次虚拟扫描，图9中显示了一个示例。请注意，点样本在靠近相机的区域更密集。

图9:从ScanNet生成的虚拟扫描

B.3 MNIST和ModelNet40实验细节

对于MNIST图像，我们首先将所有像素强度归一化到范围$[0，1]$，然后选择强度大于0.5的所有像素作为有效数字像素。然后，我们将图像中的数字像素转换为坐标在$[1，1]$范围内的2D点云，其中图像中心为原点。创建扩充点是为了将点集增加到一个固定的基数(在我们的例子中是512)。我们抖动初始点云（随机平移高斯分布$\mathcal{N}(0,0.01)$并裁剪为0.03）以生成增强点。对于ModelNet40，我们基于表面（face）面积从CAD模型表面均匀采样N个点。

对于所有实验，我们使用学习率为0.001的Adam [9]优化器进行训练。对于数据扩充，我们随机缩放目标，扰动目标位置以及点样本位置。我们还遵循[21]随机旋转目标，用于ModelNet40数据扩充。我们使用TensorFlow和GTX 1080，Titan X进行训练。所有层都在CUDA中实现运行GPU。训练我们的模型收敛大约需要20个小时。

B.4 ScanNet实验细节

为了从ScanNet场景中生成训练数据，我们从初始场景中采样1.5m×1.5m×3m的立方体，然后保留这些立方体，其中≥2%的体素被占据，并且≥70%的表面体素具有有效注释(这与[5]中的设置相同)。我们对这样的训练立方体进行动态采样，并沿着垂直轴随机旋转它。增加的点被添加到点集以形成固定的基数(在我们的例子中是8192)。在测试期间，我们类似地将测试场景分成更小的立方体，首先获得立方体中每个点的标签预测，然后合并来自同一场景的所有立方体中的标签预测。如果一个点从不同的立方体中得到不同的标签，我们将进行多数投票来得到最终的点标签预测。

B.5 SHREC15实验细节

我们在每个形状上随机抽取1024个点进行训练和测试。为了生成输入的内在特征，我们提取100维WKS，HKS和多尺度高斯曲率，导致每个点的300维特征向量。然后我们进行PCA将特征维度降低到64。我们使用[23]之后的8维嵌入来模拟测地距离，用于在选择点邻域时描述我们的非欧式度量空间。

C 更多实验

在本节中，我们提供了更多的实验结果来验证和分析我们提出的网络架构。

C.1 语义部分分割

按照[32]中的设置，我们评估我们在部分分割任务上的方法，假设每个形状的类别标签是已知的。以点云表示的形状作为输入，任务是预测每个点的部分标签。该数据集包含来自16个类的16881个形状，总共标注了50个部分。我们使用[4]之后的官方训练测试拆分。

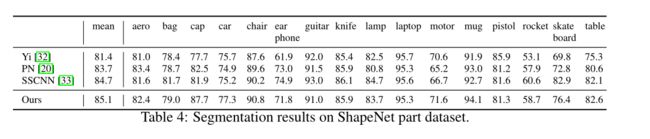
我们用每个点的法线方向来更好地描绘底层（underlying）形状。这样，我们可以摆脱手工制作的几何特征，如[32，33]中所使用的。我们将我们的框架与传统的基于学习的技术[32]以及表4中最先进的深度学习方法[20，33]进行了比较。并集上的点相交(IoU)用作评估标准，在所有部分类别中取平均值。交叉熵损失在训练期间被最小化。总的来说，我们的方法实现了最佳性能。与[20]相比，我们的方法在大多数类别上表现更好，这证明了分层特征学习对于详细语义理解的重要性。请注意，我们的方法可以被视为隐式地构建不同尺度的邻近图并在这些图上进行操作，因此与图CNN方法有关，例如[33]。由于我们的多尺度邻域选择的灵活性以及集合操作单元的能力，我们可以获得比[33]更好的性能。请注意，与图卷积核相比，我们的集合操作单元要简单得多，并且与[33]相比，我们不需要进行昂贵的特征分解。这些使我们的方法更适合大规模点云分析。

表4：ShapeNet part数据集的分割结果。

C.2 邻域查询：kNN v.s. Ball Query

这里我们比较两个选项来选择一个局部邻域。我们在论文中使用了基于半径的ball query。在这里，我们还试验了基于kNN的邻域搜索，并尝试了不同的搜索半径和k。在该实验中，所有训练和测试都是在具有均匀采样密度的ModelNet40形状上进行的。使用了1024个点。如表5所示，基于半径的ball query略好于基于 kNN 的方法。但是，我们推测在非常不均匀的点集中，基于kNN的查询会导致泛化能力变差。我们还观察到，稍大的半径可能有助于提高性能，可能是因为它捕获了更丰富的局部模式。

表5：邻里选择的影响。评估指标是ModelNet 40测试集上的分类准确率(%)。

C.3 最远点采样中随机性的影响

对于集合抽象层中的采样(Sampling)层，我们使用最远点采样(FPS)进行点集子采样。然而，FPS算法是随机的，并且子采样取决于首先选择哪个点。在这里，我们评估我们的模型对这种随机性的敏感性。在表6中，我们测试了在ModelNet40上训练的模型的特征稳定性和分类稳定性。

为了评估特征稳定性，我们用不同的随机种子提取所有测试样本的全局特征10次。然后，我们计算10次采样中每个形状的平均特征。然后，我们计算特征差的范数与平均特征的标准差。最后，我们对表中报告的所有特征尺寸的所有标准偏差进行平均。由于特征在处理之前被归一化为0到1，0.021的差异意味着特征范数的2.1%的偏差。

对于分类，我们在所有ModelNet40测试形状上仅观察到0.17%的测试精度标准偏差，这对于采样随机性是稳健的。

表6：FPS中随机性的影响（使用ModelNet40）。

C.4 时间和空间复杂性

表7总结了基于几个点集的深度学习方法之间的时间和空间成本比较。我们使用带有单个GTX 1080的TensorFlow 1.1以批量大小8记录前向时间。第一批被忽略，因为有一些GPU准备。虽然PointNet(vanilla)[20]具有最好的时间效率，但是我们没有密度自适应层的模型以相当快的速度实现了最小的模型大小。值得注意的是，我们的MSG，虽然在非均匀采样数据中具有良好的性能，但由于多尺度区域特征提取，它的成本是SSG版本的2倍。与MSG相比，MRG更有效，因为它使用跨层的区域。

表7:几个网络的模型大小和推理时间(正向传播)。