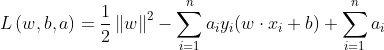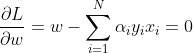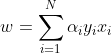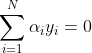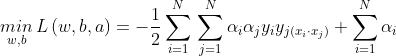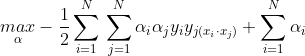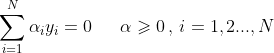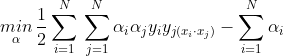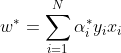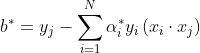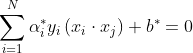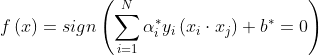SVM支持向量机学习笔记（1） —— 线性可分支持向量机与硬间隔最大化

一、什么是支持向量机

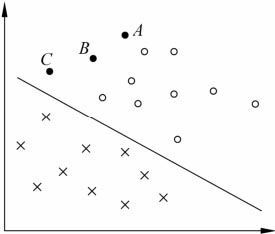
支持向量机就是要通过找支持向量来找划分超平面。考虑一个二类分类问题，分离超平面将特征空间划分为两部分，一部分是正类，一部分是负类。一般地，当训练数据集线性可分时，存在无穷个分离超平面可将两类数据正确分开。 感知机利用误分类最小的策略，求得分离超平面，不过这时的解有无穷多个。线性可分支持向量机利用间隔最大化求最优分离超平面，这时，解是唯一的。

1.线性可分支持向量机：

给定线性可分训练数据集，通过间隔最大化或等价地求解相应的凸二次规划问题学习得到的分离超平面为 ：

2.分类决策函数为：

称为线性可分支持向量机。

二、函数间隔和几何间隔

一般来说，一个点距离分离超平面的远近可以表示分类预测的确信程度。

1.函数间隔：

对于给定的训练数据集T和超平面(w,b)，定义超平面(w,b)关于样本点(xi，yi)的函数间隔为：。

定义超平面(w,b)关于训练数据集T的函数间隔为超平面(w,b)关于T中所有样本点(xi，yi)的函数间隔之最小值，即 。 

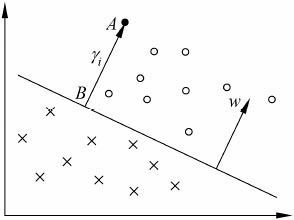
如上图，点A 与超平面(w,b)的距离由线段AB给出，记作，其中， 。

得，

2.几何间隔：

对于给定的训练数据集T和超平面(w,b)，定义超平面(w,b)关于样本点(xi，yi)的几何间隔为： 定义超平面(w,b)关于训练数据集T的几何间隔为超平面(w,b)关于T中所有样本点(xi,yi)的几何间隔之最小值，即

3.函数间隔和几何间隔的关系：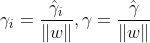

三、间隔最大化

支持向量机学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。对线性可分的训练数据集而言，线性可分分离超平面有无穷多个，但是几何间隔最大的分离超平面是唯一的。这里的间隔最大化又称为硬间隔最大化。

间隔最大化的直观解释是：

不仅将正负实例点分开，而且对于离超平面最近的点也有足够大的确信度将它们分开。

下面考虑：如何求得一个几何间隔最大的分离超平面，即最大间隔分离超平面。

   

 

事实上，函数间隔的w和b按比例改变对上面最优化问题的不等式约束没有影响，对目标函数的优化也没有影响。                                                                                                                              

因此，就可以取＝1。将＝1代入上面的最优化问题，注意到最大化和最小化是等价的，于是就得到下面的线性可分支持向量机学习的最优化问题：

引进拉格朗日乘子，使条件和公式写到一起。

其中≥0，i＝1,2,…,N，a＝(a1,a2,…,aN)T为拉格朗日乘子向量，λ为拉格朗日乘子，λ≥0。

根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题：

①求

将拉格朗日函数L(w，b,a)分别对w,b求偏导数并令其等于0。

得,   

将式代入拉格朗日函数，即得

②求对a的极大，即是对偶问题

将式的目标函数由求极大转换成求极小，就得到下面与之等价的对偶最优化问题：

定理，设是对偶最优化问题的解，则存在下标j，使得，求得原始最优化问题的解：

由此可知，

1.分离超平面:

2.分类决策函数: