基于群智能的路径规划算法（三）------遗传算法

   本系列文章主要记录学习基于群智能的路径规划算法过程中的一些关键知识点，并按照理解对其进行描述和进行相关思考。

   主要学习资料是来自 小黎的Ally 的 《第2期课程-基于群智能的三维路径规划算法》，视频链接如下（点击链接可跳转）：

   https://space.bilibili.com/477041559/channel/seriesdetail?sid=863038

   本篇文章是本系列的第三篇文章 ：遗传算法

---

   一、遗传算法简介

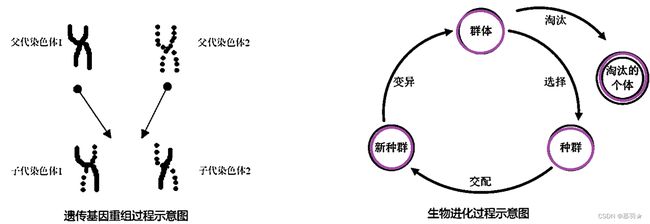
   遗传算法(Genetic Algorithm，GA)源于自然界“自然选择”和“优胜劣汰”的进化规律，是进化计算的一个分支，是一种模拟自然界生物进化过程的随机搜索算法。简单易懂、通用、鲁棒性强、适合并行处理，可用于解决各种复杂优化问题。

   通常，蚂蚁会以较大的概率优先选择信息素浓度较高的路径，并释放一定量的信息素，以增强该条路径上的信息素浓度，这样，会形成一个正反馈。最终，蚂蚁能够找到一条从巢穴到食物源的最佳路径，即距离最短。

---

   二、遗传算法相关概念和术语

   （1）染色体:携带基因信息的数据结构，不同的染色体组合表征不同的问题解。

   （2）个体(individual) :不同的染色体组合就代表一个个体;

   （3）种群(population):个体的集合，该集合内个体数称为种群的大小;

   （4）进化(evolution):种群的不断迭代使其品质不断改良;

   （5）适应度(fitness) :个体适应环境性能的评价指标（目标函数);

   （6）选择(selection):指以一定的概率从种群中选择若干个体进行交配的操作;

   （7）交叉(crossover):在两个染色体的某一相同位置处DNA被切断，其前后两串别交叉组合形成两个新的染色体，又称基因重组，俗称“杂交”;

   （8）变异(mutation):种群在迭代过程中，基因会产生突变，也即是染色体发生变异，这些新的染色体表现出新的性状;

---

   三、将蚁群算法应用于路径规划

   将遗传算法的染色体视为三维空间的控制点，即一个染色体对应着一个控制点，显然染色体个数越多，控制点越多，最终生成的三维路径越有可能接近理论最优解。

   交叉操作可以考虑将某两个个体的染色体(控制点的x/y/z坐标序列)进行两两交换

   变异操作可以考虑将某个个体的某一个染色体(控制点）的x/y/z坐标用另一个随机数代替。

---

   四、算法流程

---

   ① Step1:随机产生一组初始个体构成初始种群，并评价每一个个体的适应度;

   ② Step2:判断算法收敛准则是否满足。若满足则输出搜索结果;否则执行以下步骤;

   ③ Step3:根据适应度大小以一定概率按照轮盘赌法执行选择操作;

   ④ Step4:按交叉概率执行交叉操作;

   ⑤ Step5:按变异概率执行变异操作;

   ⑥ Step6:返回Step2.

---

   五、轮盘选择法

   轮盘赌的核心思想就是对于每个待选择的点，其对应的概率越大，被选中的可能性就越大，通过将每个点对应的概率除以所有点对应概率之和的方式来对每个点对应的概率进行处理，处理后，每个点对应的概率相加即为1，然后将这些点依次摆放在0~1的一维数轴上，其概率值越大，所占用的数轴长度就越大（注意跟摆放位置无关，可任意摆放），摆放完成后每个点也就对应于0 ~ 1数轴上一个小区间，比如第1个点的概率是0.05，第2个点的概率是0.03，第3个点的概率是0.1 … …，则第1个点对应的区间为0 ~ 0.05，第2个点对应的区间为0.05 ~ 0.08 ，第3个点对应的区间率为0.08 ~ 0.18，以此类推，这样我们随机产生一个0 ~ 1之间的随机数，该随机数落在那个区间，那个点即为被选中的点。

---

   六、编程实现思路

   对 小黎的Ally 提供的程序 的实现思路总结如下：

   首先初始化种群，按照设定的种群数量和每条路径关键点个数进行种群初始化，在设定的空间范围内随机生成每个个体的路径关键点，然后对每个个体随机生成的关键点按照x、y，z的坐标值从小到大重新排序，使得该个体的关键点中坐标值小的点放在前面，即后一个关键点的x，y，z值均大于前一个关键点的x，y，z值。使用B样条曲线把关键点拟合成路径，并计算种群中每个个体的适用度（依然以路径长度作为适应度），并判断是否更新个体最优及种群最优，完成初始化。

   思考：这里对随机生成的关键点进行排序的实现方式有一定的缺陷，仅适用于程序中设定的起点位于地图的左下角，终点位于地图右上角的这种情况，鲁棒性较差，修改起点或终点坐标后，效果可能会很差。所以程序进行实现，能够自动计算从任意起点到任意终点的方向，并按照自动计算出的方向进行排序。

   然后，按照设定的迭代次数开始进行循环迭代，在每次迭代中，先按照轮盘赌的方法（在本程序中适用度越低的个体，即路径越优的个体，被选中的概率越大）按照设定的选择比率选出一定数量的个体作为父代，然后进行交叉操作，将选出来的父代中每两个分为一组产生下一代个体，产生方式为先将选出的父代复制一份生成初始化的子代，然后对于每组均产生一个大于0小于每条路径关键点个数（也就是染色体个数）的随机数，以该随机数为分界点，交换每组初始化子代的部分关键点，比如某组的两个父代为 1 2 3 4 5 6 和 9 8 7 6 5 4，假设位于0~6的随机数为4，生成的子代为 1 2 3 4 5 4 和 9 8 7 6 5 6 。接下来依旧按照跟初始化步骤介绍的排序操作一样，对新生成的子代个体的坐标值进行重新排序，然后按照变异概率对新生成的子代进行变异操作，就是以随机数来取代某些关键点，并重新进行排序。然后将子代和这些子代的父代组成新的种群（之前没被选择作父代的个体即为被淘汰的个体），然后计算新的种群的适应度，并判断是否更新个体最优和群体最优。

   本轮迭代结束，开始进行下一次迭代 ，直至完成设定的迭代次数

---

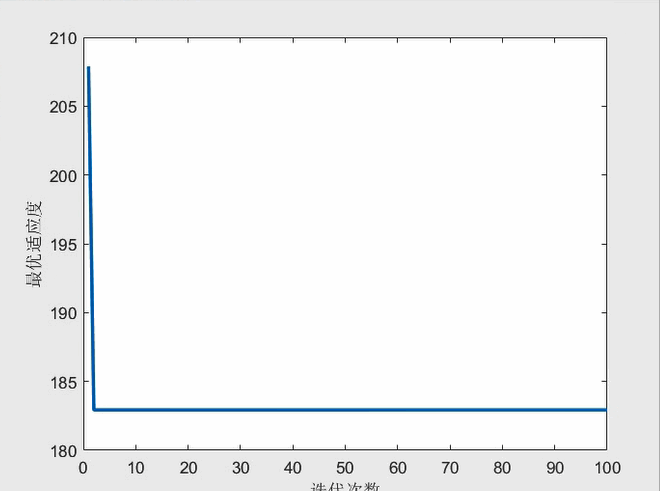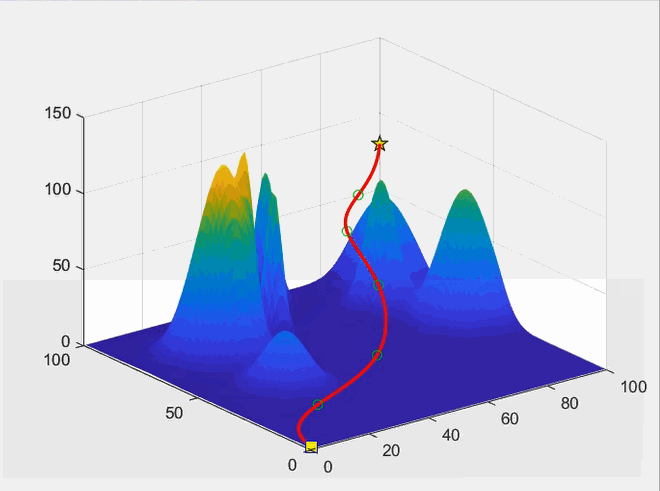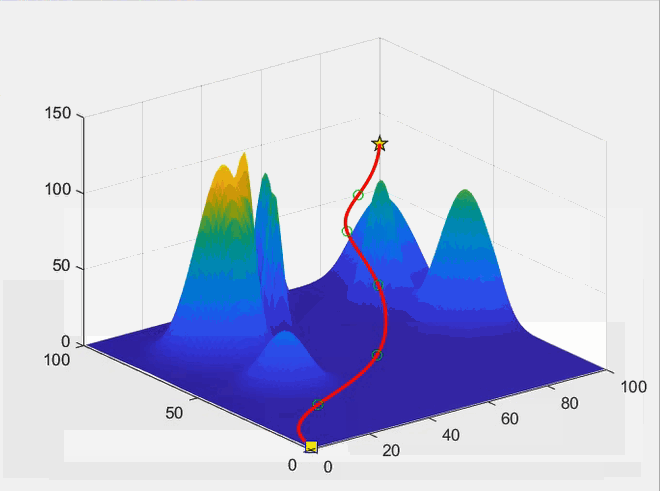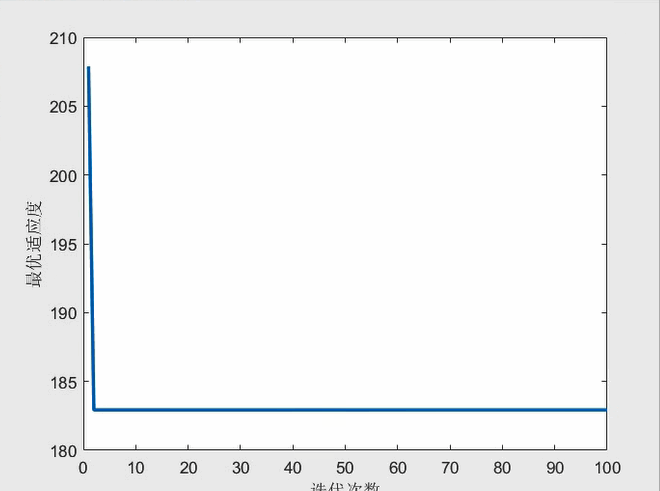
   七、运行效果示例：

---

---

   上面的示例中100次迭代后的适应度为182.93，而理论最优适应度为160.75，可知算法陷入了局部最优，且100次迭代耗时达到了1分40秒，规划效率和路径质量均不理想。

---