一篇文章带你走进深度学习
文章目录
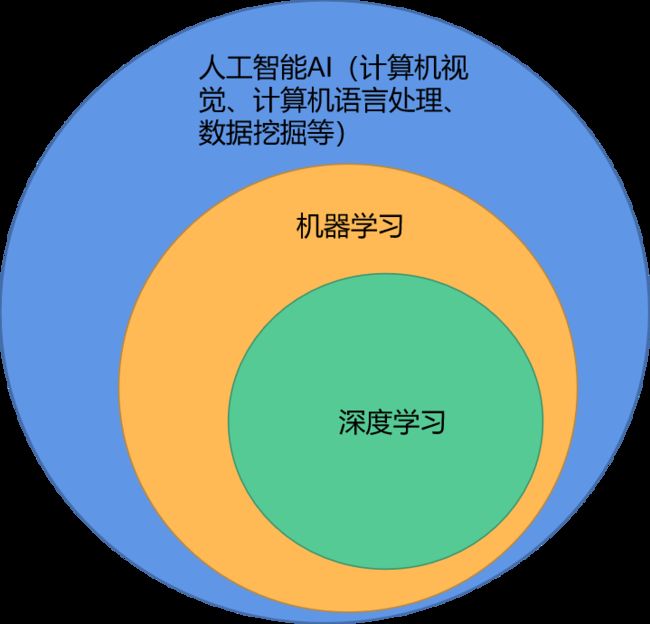
- 1.深度学习
-
- 1.1机器学习的基本流程
- 1.2深度学习的原理
- 1.3深度学习的应用
- 1.4计算机视觉
- 2.神经网络
-
- 2.1前向传播
-
- 2.1.1神经网络的基础
- 2.1.2损失函数
- 2.1.3Softmax分类器
- 2.2 反向传播
-
- 2.2.1计算偏导数
- 2.3神经网络架构细节
-
- 2.3.1正则化
- 2.3.2激活函数
- 3.神经网络过拟合解决方法
-
- 3.1数据预处理
- 3.2参数初始化
- 3.3DROP-OUT
- 4.神经网络的总结
- 5.卷积神经网络应用领域
-
- 5.1计算机视觉CV领域发展
- 5.2卷积神经网络的应用场景
- 5.3卷积网络与传统网络的区别
- 5.4卷积神经网络整体架构
- 5.5卷积层
-
- 5.5.1图像颜色通道
- 5.5.2卷积特征值计算方法
- 5.5.3步长与卷积核大小对结果的影响
- 5.5.4特征图尺寸计算
- 5.5.5卷积参数共享
- 5.5.6卷积层总结
- 5.6池化层
- 6.整体网络架构
- 7.经典网络Alexnet
- 8.VGG网络架构
- 9.残差网络Resnet
- 10.感受野的作用
- 11.RNN网络构架解读
- 12.LSTM网络构架解读
1.深度学习
- 深度学习电子书
- 深度学习电子书中源代码
- 深度学习在线课程
1.1机器学习的基本流程
- 第一步:数据获取
- 第二步:特征工程(最重要的一点)
- 第三步:选择一个算法建立模型
- 第四步:评估与应用
对数据做处理之后,我们得思考如何提取特征,从而得到更有价值的输入,有没有一种算法,就是拿到数据之后,可以自动提取特征,深度学习是跟人工智能最贴切,即解决人工的那部分,我们可以让网络真正的去学习什么特征是比较合适的,这就是深度学习能够达到的一种境界。深度学习是机器学习的一部分,也是最大的一部分,主要就是解决了特征工程。
1.2深度学习的原理
特征工程的作用:
- 数据特征决定了模型的上限
- 预处理和特征提取是最核心的
- 算法与参数选择决定了如何逼近这个上限
特征如何提取:
比如文本、图像等如何去提取特征,我们要尽可能多的去想找个特征是如何做的权重参数
深度学习的核心:
有输入数据之后,会神经网络就是一个黑盒子进行一个自动的特征提取,这些特征能够让计算机认识,所以深度学习的核心就是怎么样去提取特征
1.3深度学习的应用
- 参数很多,但是速度可能很慢
- 常见应用:人脸识别、无人驾驶、医疗方面等 链接: 最庞大的图像数据集,收集图像然后标注图像
- 数据集样例:CIFAR-10(10类标签、50000个训练数据、10000个测试数据、大小均为32*32)
1.4计算机视觉
- 图像分类任务
- 图像表示:在计算机中图像就是一个个小矩阵组成的,一张图片被表示成三维数组的形式,每个像素的值从0到255,0代表越暗,255代表越亮,255×255×3,其中3是颜色通道,RGB值
- 测试数据跟每一个训练数据进行比较,距离算出来,
2.神经网络
- 神经网络不应该称为一种算法,把他当作一个特质提取的方法更为贴切,无论还在机器学习、数据挖掘、或者其他任务点当中,所有的人工智能任务,最重要的可能不是算法,而是数据层面上,就比如一个人要去做一个好菜好饭,没有好食材能做出来吗,所以特征是非常重要的。
- 神经网络分为两大模块:一个是前向传播,一个是反向传播
2.1前向传播
2.1.1神经网络的基础
- 线性函数:从输入到输出的映射 f ( x , W ) = W x + b f(x,W)=W_x+b f(x,W)=Wx+b
其中, x x x对应一个像素点, W W W意思是parameters是每个参数对应的权重(取决定性的作用), b b b是bias起到微调的作用
2.1.2损失函数
-
定义:损失函数是用来衡量,当前这组权重参数做完之后的一个结果
-
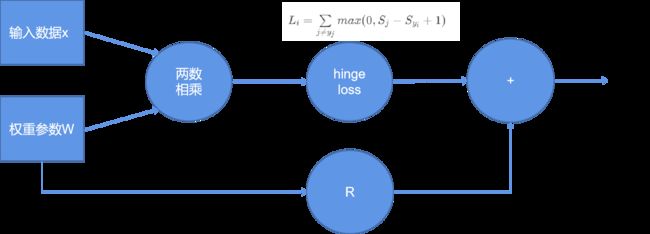
公式: L i = ∑ j ≠ y j m a x ( 0 , S j − S y i + 1 ) L_i=\sum\limits_{j\ne y_j}max(0,S_j-S_{y_i}+1) Li=j=yj∑max(0,Sj−Syi+1)
其中, S j S_j Sj是该图像属于其他类别, S y i S_{y_i} Syi是该图像属于正确类别的,加1相当于加 Δ \Delta Δ(一个容忍程度):即算出错误类别-正确类别+ Δ \Delta Δ的值,与0比较大小,取其中较大值,所以等于0时,为没有误差 -
L = 1 N ∑ i = 1 N ∑ j ≠ y j m a x ( 0 , f ( x i ; W ) j − f ( x i ; W ) y i + 1 ) + λ R ( W ) L=\frac 1 N \sum\limits_{i=1}^N \sum\limits_{j\ne y_j}max(0,f(x_i;W)_j-f(x_i;W)_{y_i}+1)+\lambda R(W) L=N1i=1∑Nj=yj∑max(0,f(xi;W)j−f(xi;W)yi+1)+λR(W)
其中,加号前半部分是data_loss(即数据在当前损失函数当中得到的一个损失),加号后半部分是正则化惩罚项(即由这组模型一个权重参数 W W W所带来的一个损失,跟数据是没有任何关系的,只考虑权重参数, R ( W ) = ∑ k ∑ l W k , l 2 R(W)=\sum_k\sum_lW_{k,l}^2 R(W)=∑k∑lWk,l2,就是 w 1 2 + w 2 2 + w 3 2 + … … + w l 2 w_1^2+w_2^2+w_3^2+……+w_l^2 w12+w22+w32+……+wl2再乘上一个 λ \lambda λ, λ \lambda λ越大消减的越大,也就是我不希望过拟合,我希望正则化大一些, λ \lambda λ数值较小就是意思意思得了)注:过拟合就是只关注其中一个种类,而不关注其他种类
2.1.3Softmax分类器
-
归一化: P ( Y = k ∣ X = x i ) = e s k ∑ j e s j P(Y=k|X=x_i)=\frac {e^{s_k}} {\sum_j e^{s_j}} P(Y=k∣X=xi)=∑jesjesk
其中, s = f ( x i ; W ) s=f(x_i;W) s=f(xi;W) -
计算损失值: L i = − l o g P ( Y = y i ∣ X = x i ) L_i=-logP(Y=y_i|X=x_i) Li=−logP(Y=yi∣X=xi)
-
先得到各类别的一个得分值 x x x,然后算出各自对应的 e x e^x ex值,再将该值进行归一化,得到概率值,例如其中一种的概率值比所有种类的概率值,根据对数函数的图像可知,对数函数中x是0-1时对应的y值是负数,所以我们给式子前面加上负号,并且x越接近于1,损失值越小,也就是说正确的类别的概率值越接近1的越没有损失
-
回归任务最终是要预测一个值,是由得分值去计算一个损失
-
分类任务是由概率值去计算一个损失
2.2 反向传播
- 前向传播:有了 x x x和 w w w是可以计算出一个损失的
- 反向传播:神经网络的实质就是更新 w w w,损失值很高就是指 w w w不好,那么反向传播就是调整 w w w,能让损失值下降,这就是一种优化,采用梯度下降方法
2.2.1计算偏导数
-
f ( w , x ) = 1 1 + e − ( w 0 x 0 + w 1 x 1 + w 2 ) f(w,x)=\frac 1 {1+e^-{(w_0 x_0+w_1 x_1+w_2)}} f(w,x)=1+e−(w0x0+w1x1+w2)1
比如有三个人要计算 w w w的值,就是第一个人先算出 x 0 w 0 x_0w_0 x0w0的值,然后第二个人再将该值乘 w w w得出 w 1 w_1 w1,接着第三个人再算出 w 1 w_1 w1乘 w w w得到 w 2 w_2 w2,即 [ ( x w 1 ) w 2 ] w 3 [(xw1)w2]w3 [(xw1)w2]w3 -
公式如下: σ ( x ) = 1 1 + e − x \sigma(x)=\frac 1 {1+e^{-x}} σ(x)=1+e−x1sigmoid function d σ ( x ) d x = e − x ( 1 + e − x ) 2 = ( 1 − σ ( x ) ) σ ( x ) \frac {d\sigma(x)} {dx}=\frac {e^{-x}} {{(1+e^{-x}})^2}={(1-\sigma{(x)})}\sigma(x) dxdσ(x)=(1+e−x)2e−x=(1−σ(x))σ(x)
-
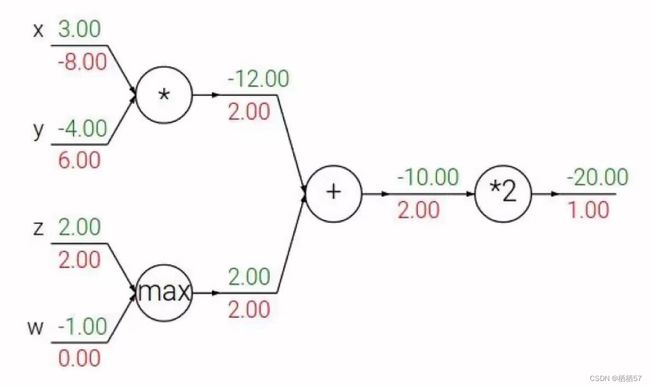
加法门单元:均等分配
-
MAX门单元:给最大的
-
乘法门单元:互换的感觉
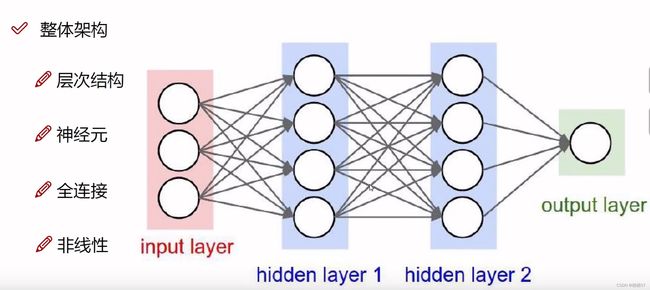
2.3神经网络架构细节
- 我们对数据进行变换的目的是让计算机能够识别
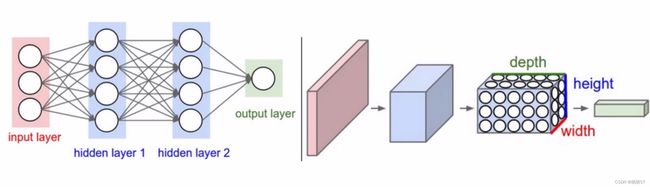
- 全连接层的含义:输入层与隐藏层的每个圆圈都连着一起了,就是全连接
- 比如前面传入的数据是身高、年龄、体重,我们把数据进行变换,转换成四个特征,年龄乘0.1+身高乘0.2+体重乘0.3=第一个圆圈的值,神经网络是一个黑盒子,我们也不知道里面进行了怎样的变换
- 但是做一个矩阵乘法,将三个圆圈变成四个圆圈,也就是 x × w x×w x×w之后得到的结果
- 非线性变换:在每一步变成4个圆圈之前,先找一个非线性函数做一个映射,sigma函数或者max函数
- 基本架构: f = W 2 m a x ( 0 , W 1 x ) f=W_2max(0,W_1x) f=W2max(0,W1x)
- 继续堆叠一层: f = W 3 m a x ( 0 , W 2 m a x ( 0 , W 1 x ) ) f=W_3max(0,W_2max(0,W_1x)) f=W3max(0,W2max(0,W1x))
其中,max函数,当 x x x值小于0,即为0, x x x值大于0,即为 x x x - 神经网络的强大之处在于,用更多的参数来拟合复杂的数据
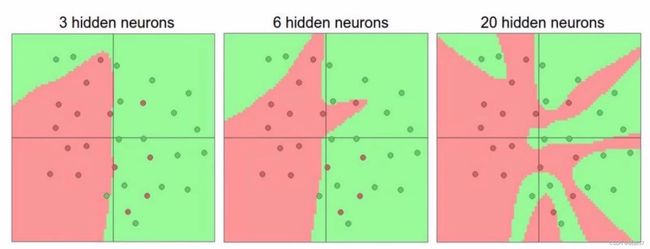
- 每一个圆圈都代表一个神经元,神经元越多,多拟合程度越大,得到的结果可能会更好,但是计算量也会更大
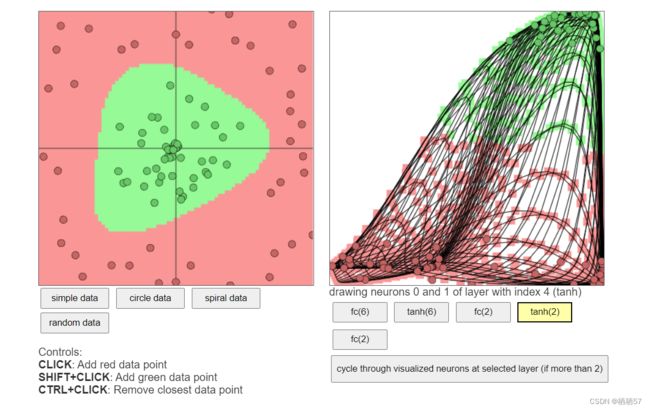
链接: 可视化展示神经网络

神经元为1,就相当于切了一刀,神经元为3就相当于切了三刀
2.3.1正则化
-
正则化的作用:惩罚力度对结果的影响
-
λ \lambda λ越小,越符合训练集的结果
-
训练集的loss+ R ( W ) R(W) R(W)的loss组成了最终的一个惩罚力度
-
我们实际看的还是测试集
-
过拟合:失去泛化能力,不能够判断出样本中异常的点,例如图一,强行将红色的点给区分出来,而那个红色的点应该是绿色的,过拟合只是在样本数据集中精确,而引入其他数据集就不太精确,俗称泛化能力差,如下图的都是会过拟合的,所以我们就需要一个具体的参数,而达到更好的效果
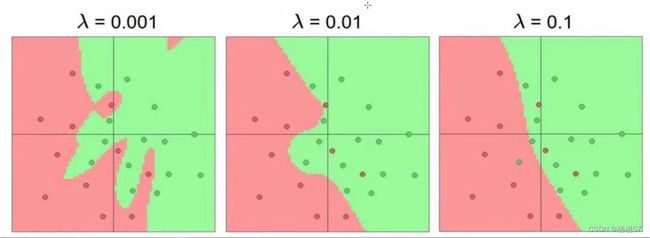
-
参数个数对结果的影响
-
神经元越多,过拟合风险越大
-
不选过拟合的,尽量选不过拟合的情况下,把结果展示的更好一些
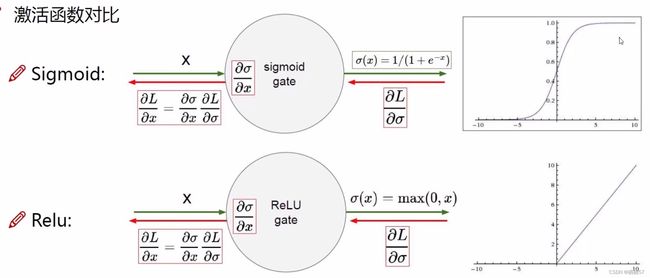
2.3.2激活函数
- 是神经网络中非常重要的一部分
- 神经网络经过一组权重参数计算完之后,要进行一个非线性的变换
- 常用的激活函数(Sigmoid,Relu,Tanh等)就列出了常见的非线性变换,激活函数是非线性变化
- Sigmoid函数中,一旦数值较大或是数值较小,梯度为0代表不进行更新,不进行传播,出现了梯度消失的现象
- 现在90%都使用Relu函数,小于0时都为0,大于0时为 x x x本身,所以梯度很好算,小于0的都剔除掉了,所以不会有梯度消失的现象
3.神经网络过拟合解决方法
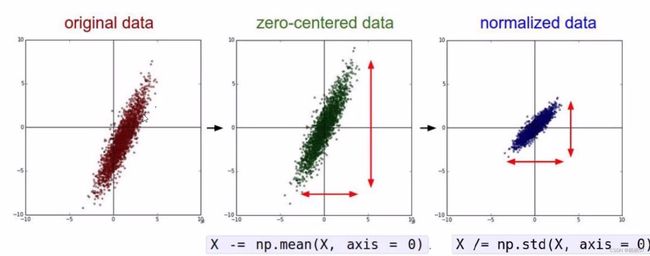
3.1数据预处理
3.2参数初始化
- 通常我们都使用随机策略来进行参数初始化
- W = 0.01 ∗ n p . r a n d o m . r a n d n ( D , H ) W=0.01*np.random.randn(D,H) W=0.01∗np.random.randn(D,H)
例如一些参数值起伏很大,一会很大,一会很小,那么我们乘上0.01就可以将数值都变得很小,在函数图像上基本看不到太大的起伏
3.3DROP-OUT
- 传说中的七伤拳(伤敌七分,自损三分,互相伤害的感觉)
- 过拟合是神经网络非常头疼的一个大问题
- 通常层数比较多,神经元也比较多,这就造成整个神经网络过拟合风险特别大
- 之前说了可以加正则化 R ( W ) R(W) R(W)
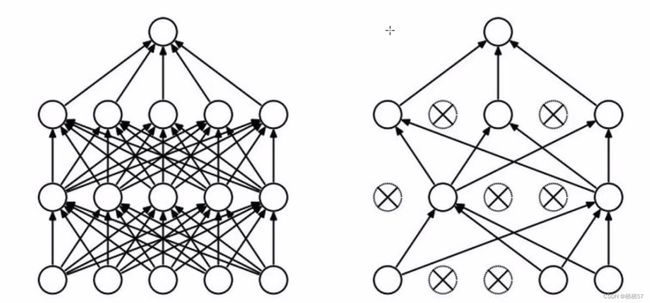
- 左图是完整的神经网络,是一个全连接的,跟与其他神经元全部连在一起
- 右图在神经网络训练的过程中(注意是训练的过程),在每一层随机杀死一部分神经元,第一次训练可能第一层2、4不用,而第二次训练是3、4不用
4.神经网络的总结
- 例如有数据 x 1 x 2 x 3 x_1 x_2 x_3 x1x2x3
- 先进行数据预处理,并不是说所有数据都可以当做输入的,如文本去除停用词,图像数据进行标准化
- 预处理之后得到输入层
- 输入层和隐藏层之间是 w 1 w 2 w 3 w_1 w_2 w_3 w1w2w3,用这些权重参数来连接的
- 在与 w w w进行相乘之前,会经过一个Relu激活函数,进行非线性转化
反向传播
- 计算loss值
- loss先对 w 3 w_3 w3求偏导,算出 w 3 w_3 w3对结果做出了怎样的变化
- 再依次对Relu函数, w 2 w_2 w2,Relu, w 1 w_1 w1求偏导,其中Relu函数值不发生变化,而 w w w值会进行更新
- 整个神经网络在计算过程当中,就是找权重参数,什么样的权重参数能够最适用于当前的任务
- 也就是说, w 1 w 2 w 3 w_1 w_2 w_3 w1w2w3 具体值算出来了,整个神经网络就做完了
多拟合
- 神经网络99%都会过拟合的
- 一旦过拟合了,我们就得想什么样的解决方案是合适的
- 方法一,加上正则化
- 方法二,加上DROP-OUT
- 还有其他各种各样的方法,层出不穷
(神经网络一些细节一直在更新,但是整体的框架是不会变的)
5.卷积神经网络应用领域
5.1计算机视觉CV领域发展
- 卷积神经网络主要就是应用在计算机视觉任务当中的
- 深度学习使计算机视觉取得了很好的成就
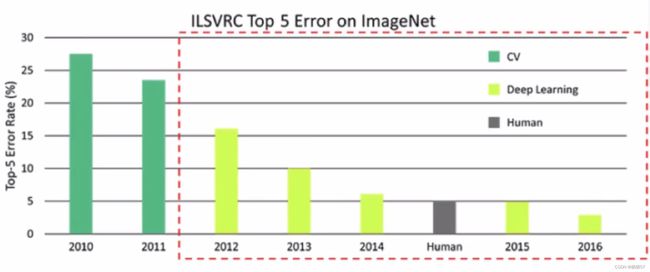
- 通过上图我们可以观察到(数值表示判断错误率),在2012年引入深度学习之前,错误率是很高的,而2015年已经可以达到跟人类判别错误率基本相同的水平了,2016年至今,技术水平仍在提高
5.2卷积神经网络的应用场景
- 基本上的视觉任务都能由CNN网络实现
- 卷积神经网络就是解决上述内容中,过拟合、参数过多、神经元多、矩阵大等问题的
- 目前只要涉及图像方面的,都能用到,例如医学细胞检测、无人驾驶、人脸识别
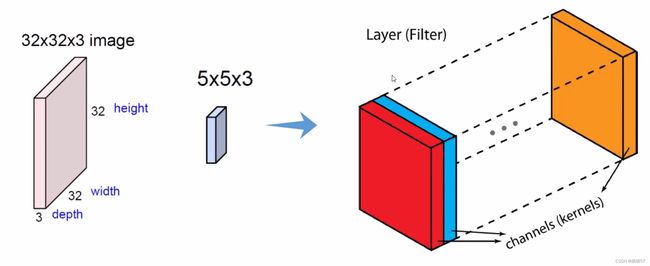
5.3卷积网络与传统网络的区别
- 右边是卷积神经网络,输入的不再是点,而是28×28×1三维的图像(H×W×C),左边传统的输入只是一列特征
- 不会把数据拉成向量,而是直接对样本进行特征提取
- 还添加了depth深度
5.4卷积神经网络整体架构
- 输入层:是一个图像数据28×28×1(该图像是一个灰度,所以乘1)
- 卷积层:主要就是提取特征(后面会具体讲解)
- 池化层:压缩特征(后面会具体讲解)
- 全连接层:通过一组权重矩阵 w w w,例如前面讲述过的将输入层和隐藏层连接在一起
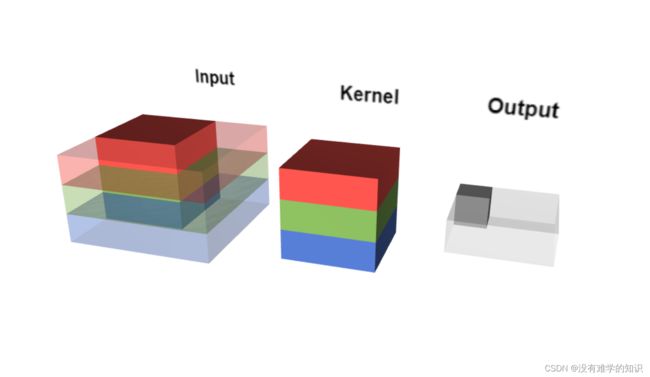
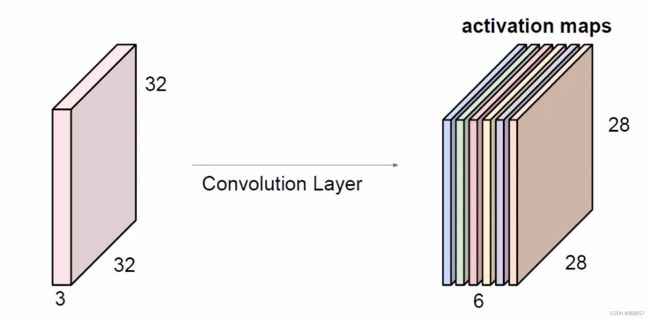
5.5卷积层
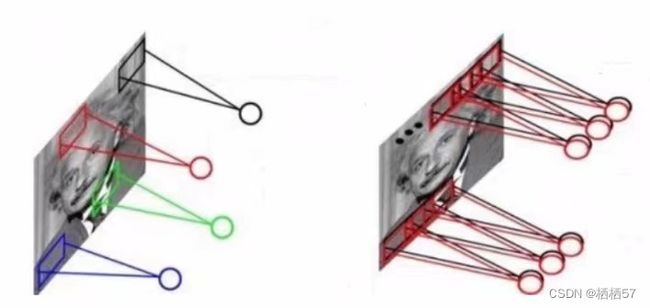
- 比如图像是只猫,边界的特征以及和猫的特征就是不一样的,所以我们要对不同的区域提取出不同的特征,我们得知道边界的特征不是那么重要,而猫的特征是很重要的
- 所以我们将一张图像分为很多不同的部分,不同的地方需要区别的处理
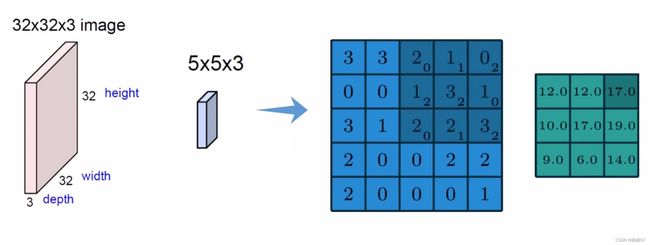
- 比如改图像第一步分割成5×5×3的,如蓝色的立方体,
- 第二步由权重参数得到特征值,上图的权重矩阵就是 [ 0 , 1 , 2 2 , 2 , 0 0 , 1 , 2 ] \begin{bmatrix} 0,1,2\\2,2,0\\0,1,2\end{bmatrix} ⎣ ⎡0,1,22,2,00,1,2⎦ ⎤,得到的绿色的就是特征图
5.5.1图像颜色通道
5.5.2卷积特征值计算方法
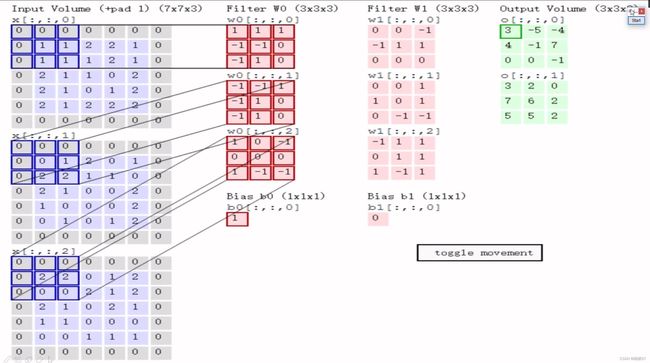
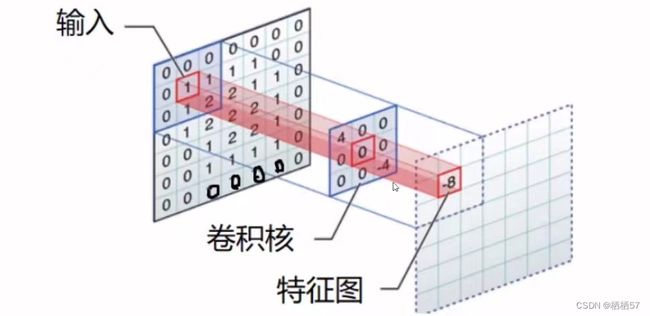
- 先随机初始化一个权重参数,三通道对应的 w w w矩阵值都是不一样的
- 矩阵与矩阵相乘时,采用内积,即矩阵对应位置相乘之后的结果相加,例如上图左侧第一个图与 w 0 w_0 w0相乘之后就是0×1+0×1+0×1+0×(-1)+1×(-1)+1×0+0×(-1)+1×1+1×0=0,第二个是2,第三个是0,
- 之后再将上面求得的值相加0+2+0+ b 0 b_0 b0,别忘记了加 b 0 b_0 b0,偏置参数, b 0 b_0 b0=1,所以最终值为3,也就是上图最右侧的左上角的值3
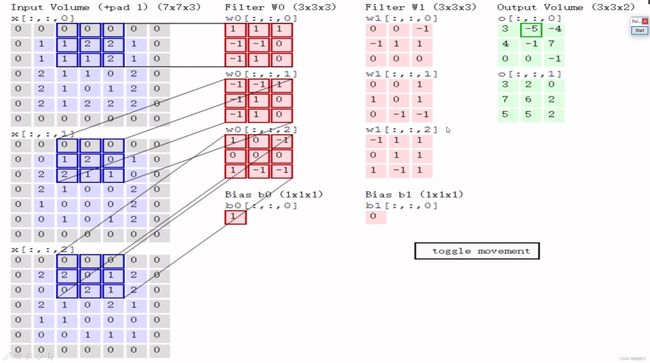
- 第一块区域做好了之后,我们会移动,此时的步长是2,然后与上面的步骤是一样的
- 其中,步长是根据输出决定的,例如该图需要3×3的输出,就得移动两个单元格
5.5.3步长与卷积核大小对结果的影响
-
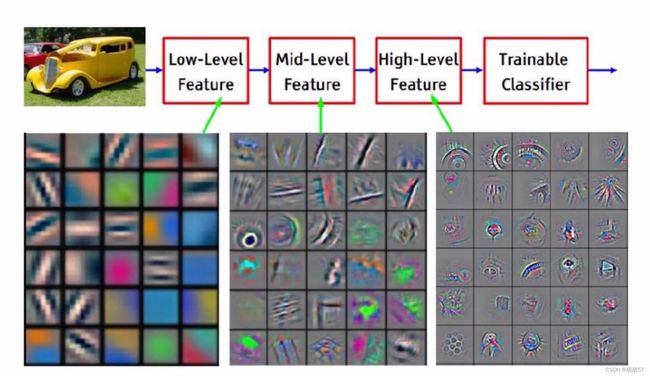
先粗力度的提取特征,然后再细力度提取特征,最后再高水平提取特征,拿高级特征进行分类
-
首先开始输入的图像(粉色立方体)中的C表示三通道
-
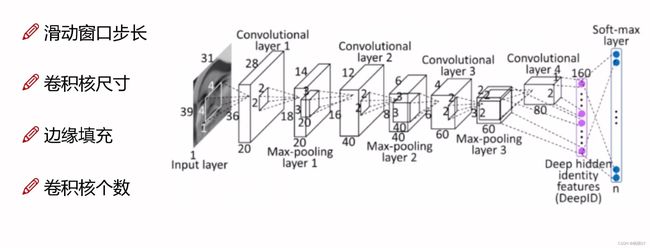
卷积层涉及的参数:
-
滑动窗口的步长:步长越小,滑动窗口越多,计算效率越慢
-
边缘填充:比如下面这张图第一行第一个括号内有一个(+pad 1)
-
我们可以观察到第一列中有紫色和灰色,其中灰色就是我们填充的,pad1就是原来是5×5的,现在变成6×6,因为我们在采用窗口进行滑动的时候,可观察到中间的部分有交集,也就是被提取的特征次数增多,而边缘的机会就很少,所以我们采用了边缘填充,让原本在边界的地方尽量往中间靠拢
-
同时为了避免添加的边界会对最终的值产生影响,我们给元素值设置为0,也被称为zero padding
-
一定程度上弥补了边界缺失的现象
5.5.4特征图尺寸计算
- H H H和 W W W的计算方法都是一模一样的
- 其中, W 1 W_1 W1、 H 1 H_1 H1表示输入的宽度、长度; W 2 W_2 W2、 H 2 H_2 H2表示输出特征图的宽度、长度; F F F表示卷积核长和宽的大小; S S S表示滑动窗口的步长; P P P表示边界填充(加几圈0),因为pad每次加的时候都是上下加一层,左右加一层,所以公式中是乘 2 P 2P 2P
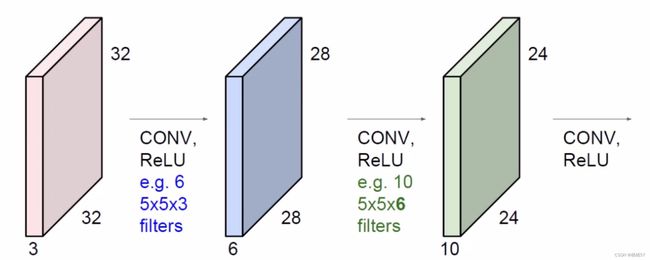
- 例如,输入数据是32×32×3的图像,用10个5×5×3的filter来进行卷积操作,指定步长为1,边界填充为2,最终输入的规模为?
- (32-5+2×2)/1+1=32,所以输出规模为32×32×10,经过卷积操作后也可以保持特征图长度、宽度不变
5.5.5卷积参数共享
- 我们在用卷积核时,矩阵里面的数值如果都是不同的话(如上图左边),参数太多了,对计算会造成麻烦,所以我们采用同一个卷积核,矩阵数值都一样(如上图右边)
- 例如,数据依旧是32×32×3的图像,继续用10个5×5×3的filter来进行卷积操作,所需的权重参数有多少个呢?
- 5×5×3=75,表示每一个卷积核只需要75个参数,此时有10个不同的卷积核,就需要10×75=750个卷积核参数,不要忘记还有b参数,每个卷积核都有一个对应的偏置参数,最终只需要750+10=760个权重参数
5.5.6卷积层总结
- 可以看到,在一张图像输入之后,我们通过一层卷积可以得到绿色的特征图
- 对于同样一张图来说,我们可以通过相乘不同的矩阵,多尺度多力度的进行特征提取,让特征图更丰富起来,如下图就是用了6个不同的矩阵,得到了6个特征图,相当于得到了一个丰富的特征(计算公式会在后面的内容中给出)
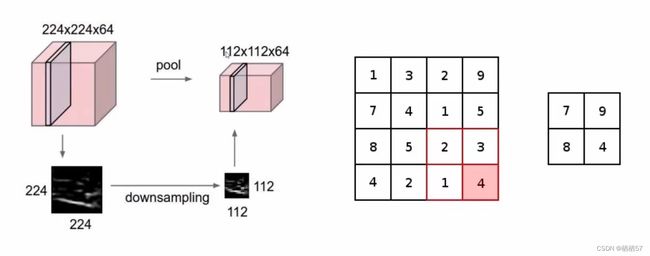
5.6池化层
- 由卷积层得到那么多特征图,卷积可以做很多次,但是如果特征图比较多呢,这时就需要引入池化层,对得到的数据进行下采样downsampling(压缩)
- 如上图,原始是224×224×64,我们通过pool(池化层)得到一个112×112×64,只会变长和宽,而不会变64,也就是卷积核的个数
- 上图的右边是将每个框内取最大值,也就是MAX POOLING,做了一个筛选,因为数值较大,意味着权重参数越大,整个网络认为该数值是比较重要的
- 还有另一种平均池化AVERAGE POOLING,取每块区域的平均值(但是现在很少用了,因为我们既然已经得到好的特征了,那么为什么还要算较差的特征呢)
- 所以基本上都是MAX POOLING,因为优胜劣汰,经过不断的实验,发现该方法效果更好
- 池化层没有涉及到矩阵的运算,只是一个筛选,所以还是比较简单的
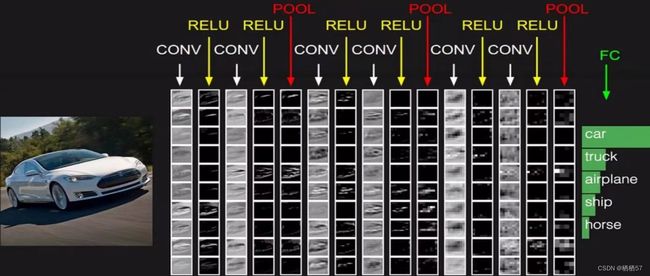
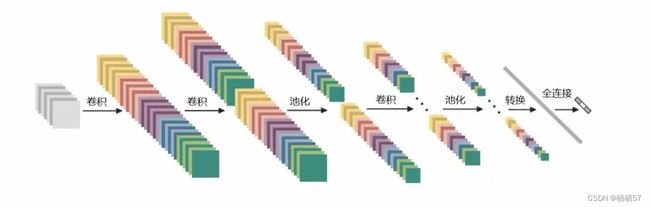
6.整体网络架构
- 先通过卷积CONV,进行特征提取
- 每一步卷积之后都会有一个RELU,进行非线性变换他们相当于一个组合
- 两次卷积一次池化
- 假设最终得到一个32×32×10的特征图,我们这个特征图是一个立体的,我们如何将这个立体的特征图转化成5个分类的概率值
- 前面的卷积和池化主要是做特征提取的,得到最终的结果还得靠全连接层FC
- 我们首先需要将32×32×10的立体图,拉成一个非常长的特征向量32×32×10=10240
- 比如上图的FC矩阵就是一个[10240,5]
- 也就是说在最后的POOL层和FC层之间还有一个拉长的操作
- 带参数计算的才能叫做一层,比如这里卷积层带参数计算,而RELU不带参数计算(没有权重参数,没有偏置参数,没有数据更新),所以说激活函数不带参数计算,因为不需要返回传播,也不需要更新数据,同理POOL层也不需要,全连接层有权重参数矩阵,所以上图一共有6+1=7层的神经网络
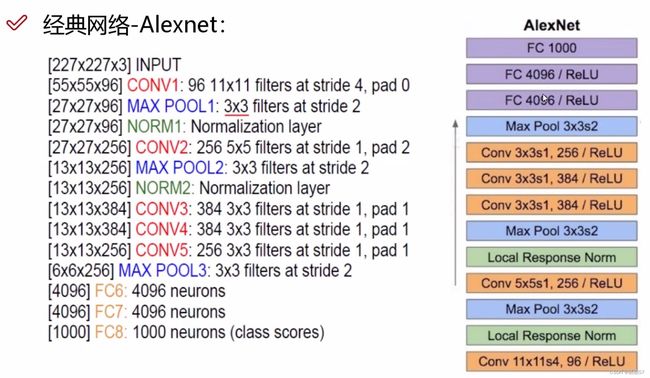
7.经典网络Alexnet
- 是很早之前的,12年夺冠的网络
- 缺点:
- 1、11乘11的filter,大刀阔斧的提取特征,现在基本上是越小越好
- 2、stride=4,太大了
- 3、pad=0,不填充
- 8层网络、5层卷积、3层全连接、还有2层Local Response Norm(这层后来被证明是没用的,所以不用去管)
8.VGG网络架构
- 14年的网络
- 有右图表中的六个版本,其中最主流的就是D版本
- 特点:
- 1、所有卷积核的大小都是3×3,意味着都是细力度进行提取
- 2、Alexnet网络只有8层,而VGG有16层/19层,所以层数是更优秀的
- 3、下图右侧图标中conv3-64表示得到64个特征图,我们知道在经过一次maxpool层之后,会损失部分特征信息,而在VGG网络中,每次经过pool层之后,都将特征图翻倍,如下图可以观察到从64-128-256-512,所以相当于用特征图的个数去弥补损失
- Alexnet要训练8小时,而VGG要训练3天
9.残差网络Resnet
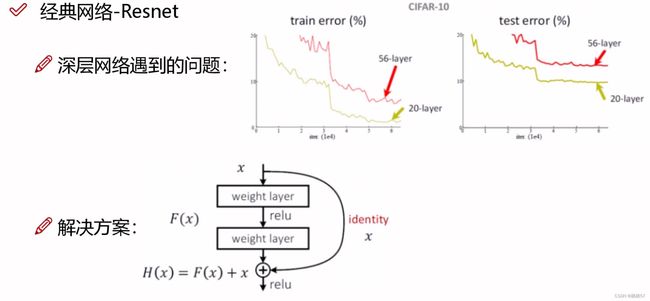
- 15年年底,出现了残差网络Resnet
- 深层网络遇到的问题,下图中的右侧两个坐标轴中可以观察出,无论是左侧(训练集),还是右侧(测试集)中,56层的效果都比20层效果差(error是错误率,所以越低效果越好)
- 20层到56层中间加36层,其中可能有些层的效果并不好
- 解决方案核心思想:如果加入的层数效果不好,那么我们就不用它,将它的权重参数设置为0
- 解决方案:假设 x x x是第20层,经过weight layer一层卷积,然后经过relu激活函数,之后再经过weight layer一层卷积,得到的结果 F ( X ) F(X) F(X),此时我们再额外的连接一条identity线,原封不动的再把20层的 x x x拿过来,现在不仅有原来的 F ( X ) F(X) F(X)结果,还有同等映射的 x x x一个结果,如果 F ( x ) F(x) F(x)得到的loss值并不好,那么就会将其中的权重参数设为0,再加上原来的 x x x,就是有个保底,至少不会比原来差
- 该残差网络将VGG救活了
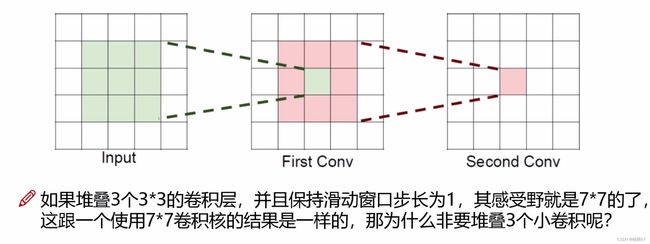
10.感受野的作用
-
Input中绿色的经过一次卷积,得到First Conv里面的绿色小方块,因此First Conv是由前面Input中3×3得到的
-
Second Conv又是由First Conv中9个上一步中类似绿色的小方块得到的,一个绿色小方块对应到Input是3×3,而9个小方块加上重叠的部分对应到Input正好是5×5
- 上图答案:假设输入大小都是 h × w × c h×w×c h×w×c,并且都使用 c c c个卷积核(得到 c c c个特征图),可以来计算一下其各自所需参数:
- 一个7*7卷积核所需参数= C × ( 7 × 7 × C ) = 49 C 2 C×(7×7×C)=49C^2 C×(7×7×C)=49C2
- 三个3*3卷积核所需参数= 3 × C × ( 3 × 3 × C ) = 27 C 2 3×C×(3×3×C)=27C^2 3×C×(3×3×C)=27C2
- 很明显,堆叠小的卷积核所需的参数更少一些,并且卷积过程越多,特征提取也会越细致,加入的非线性变换也随着增多,还不会增大权重参数个数,这就是VGG网络的基本出发点,用小的卷积核来完成体特征提取操作
11.RNN网络构架解读
-
递归神经网络RNN,在传统的神经网络基础上进行改进
-
比如特征提取与时间相关,由于时间相关性,对结果产生的影响,这就是RNN在处理时间方面的优势
-
数据在经过隐藏层之后会得到当前的特征,比如隐藏层会将数据转化成64个特征,然后64个特征经过输出会得到10个类别的输出值,前一个时刻训练的特征也会对后一个特征产生影响的,因为特征无非就是数据的一个表达,在特征上也会呈现出一个相关性,会将前一层结果保留下来,这样得到的结果会更准确一点
-
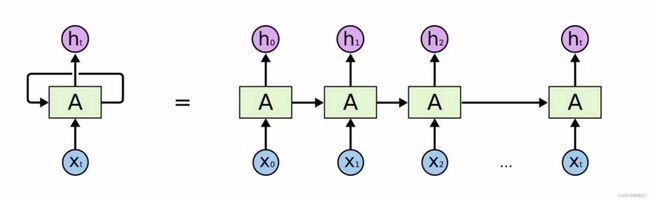
比如有多个不同的时刻, x 0 , x 1 . . . x t x_0,x_1...x_t x0,x1...xt,每个时刻都有对于的输出结果 h 0 , h 1 . . . h t h_0,h_1...h_t h0,h1...ht,代表中间结果,最后我们要选择其中的一个结果 h t h_t ht,它会将之前所有的结果综合考虑进来
-
首先得将输入数据转化成对应的特征向量,并且按照时间顺序,从前到后进行排列,得到结果之后,我们就可以来训练这个模型了,例如:单词我们使用Word2Vec进行编码,将单词编码成向量,比如将所有的单词转化成300个向量
12.LSTM网络构架解读
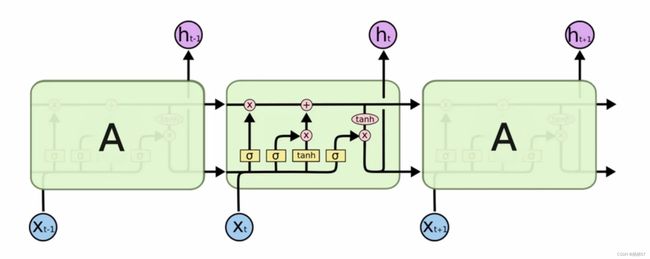
- RNN的缺点是最后一个结果会将前面的所有结果都考虑进来,但是前面的结果一定都重要吗,而且一旦记录的多了,可能就不精了,会产生误差
- LSTM就是过滤掉没必要的特征
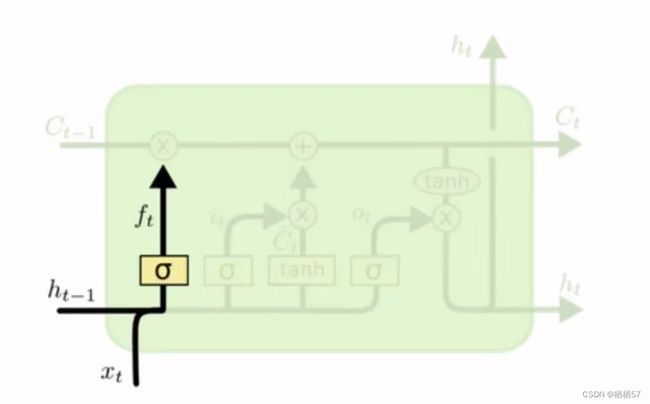
- C:控制参数,决定什么样的信息会被保留什么样的信息会被遗忘,C需要持续进行维护和更新(下图左侧粗细所示)
- 还有一些门单元,门是一种让信息选择式通过的方法(下图右侧所示)
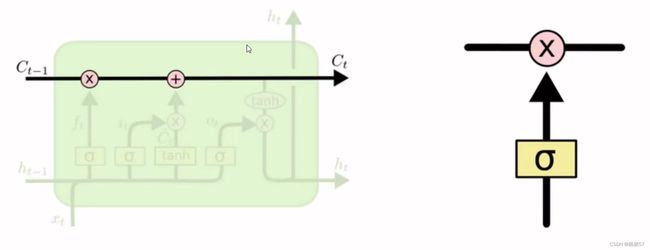
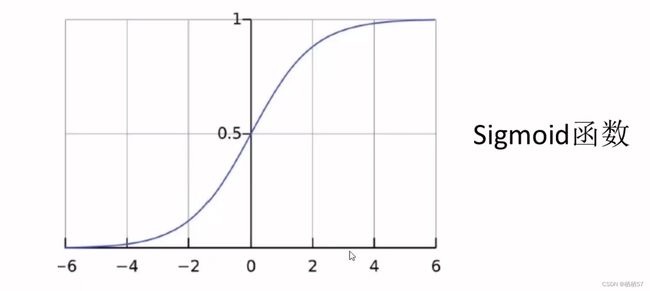
- sigmoid神经网络层和一些乘法操作
- sigmoid层输出0到1之间的数值,描述每个部分有多少量可以通过,0代表“不许任何量通过”,1就指“允许任意量通过”
- f t = σ ( W f × [ h t − 1 , x t ] + b f ) f_t=\sigma(W_f×[h_{t-1},x_t]+b_f) ft=σ(Wf×[ht−1,xt]+bf)
- f t f_t ft与 C t − 1 C_{t-1} Ct−1计算决定丢弃什么信息(如下图)
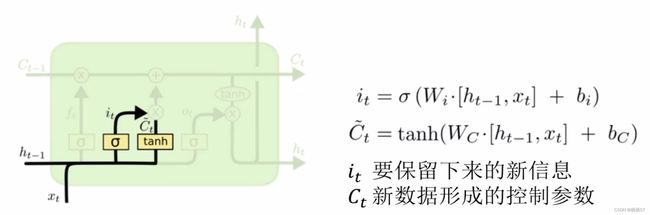
- i t = σ ( W i × [ h t − 1 , x t ] + b i ) i_t=\sigma(W_i×[h_{t-1},x_t]+b_i) it=σ(Wi×[ht−1,xt]+bi)
- C t = t a n h ( W c × [ h t − 1 , x t ] + b c ) C_t=tanh(W_c×[h_{t-1},x_t]+b_c) Ct=tanh(Wc×[ht−1,xt]+bc)
- LSTM的基本架构