【菜菜的sklearn课堂】决策树-用回归树拟合正弦曲线
视频作者:菜菜TsaiTsai
链接:【技术干货】菜菜的机器学习sklearn【全85集】Python进阶_哔哩哔哩_bilibili
import numpy as np
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80,1), axis=0)
# axis=0,沿列的方向排序数据,如果有多列,每一列数据之间自己进行排序,是独立的
# axis=1,沿行的方向排序数据;axis=None,将高维数组转化为一维并升序排序
rng = np.random.RandomState(1):一个伪随机数生成器,返回RandomState对象。随机数是用确定性的算法计算出来自 [ 0 , 1 ] [0,1] [0,1]均匀分布的随机数序列。并不真正的随机,但具有类似于随机数的统计特征,如均匀性、独立性等。
rand(80),指的是一个80个元素的一维数组,不是80行1列,或者1行80列,因为这二者都是二维数组的描述方式
由于fit接收X不接收一维特征,因此我们需要生成二维数组(数据矩阵),也就是rng.rand(80,1)
这里要注意np.random.RandomState(1).rand()和np.random.rand(),是不同的,前者是在一个固定的伪随机数生成器下生成的 [ 0 , 1 ] [0,1] [0,1]的随机数,即使我们在前面写了前者,但不经过固定的伪随机数生成器来调用rand,那么我们生成的随机数依旧无法被固定。例如现在我们固定了一个伪随机数生成器
for i in range(3): rng = np.random.RandomState(1) print(rng.rand(3)) print(np.random.rand(3)) --- [4.17022005e-01 7.20324493e-01 1.14374817e-04] [0.24854201 0.50811133 0.49999858] [4.17022005e-01 7.20324493e-01 1.14374817e-04] [0.5478054 0.59739849 0.22514079] [4.17022005e-01 7.20324493e-01 1.14374817e-04] [0.17886054 0.60591715 0.64348522]显然前者是固定的,对后者并无影响
这里有一些个人理解。可能np.random.RandomState(1).rand()调用后再调用np.random.rand(),会影响已经生成的RandomState对象,因此如果调用了np.random.rand(),我们再想使用np.random.RandomState(1).rand()生成固定随机数,需要再次得到之前的RandomState对象。即下述情况
rng = np.random.RandomState(1) for i in range(2): print(rng.rand(3)) print(np.random.rand(3)) --- [4.17022005e-01 7.20324493e-01 1.14374817e-04] [0.16401897 0.4949546 0.87024651] [0.30233257 0.14675589 0.09233859] [0.80481614 0.63129344 0.67668002]
y = np.sin(X).ravel()
# ravel()返回的是视图,修改时会影响原始矩阵
# flatten()返回一份拷贝,对拷贝所做修改不会影响原始矩阵
np.sin(X)结果是二维数组(80,1),但y必须是一维数组,因此使用ravel()降维
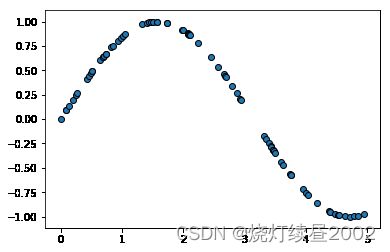
plt.figure()
plt.scatter(X, y, edgecolor='black')
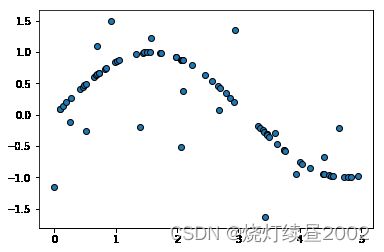
增加一个 [ − 1.5 , 1.5 ] [-1.5,1.5] [−1.5,1.5]的噪声
y[::5] += 3 * (0.5 - rng.rand(16))
# y[::5],意为每5行、每5列
plt.figure()
plt.scatter(X, y, edgecolor='black')
训练决策树
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_1.fit(X,y)
regr_2.fit(X,y)
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
# np.arange(开始点, 结束点, 步长),从开始点每次增加步长的大小,直到结束点(不包括结束点)
[:, np.newaxis]类似于reshape(-1,1),把一维变成二维
np.random.rand(5).reshape(-1,1) --- array([[0.04267956], [0.78550248], [0.26686091]]) a = np.array([1, 2, 3, 4]) print(a[:])# 切片 # 几维数组,就最多能有几个切片,但低维数组可以用newaxis填充空的部分来升维 print(a[:, np.newaxis]) # 行数是a里的元素个数,列上的数据顺序是a里元素的顺序 # 可以认为是加列的方式变为二维数组,np.newaxis写在列索引位置 print(a[np.newaxis, :]) # 列数是a里的元素个数,行上的数据顺序是a里元素的顺序 # 可以认为是加行的方式变为二维数组,np.newaxis写在行索引位置 --- [1 2 3 4] [[1] [2] [3] [4]] [[1 2 3 4]]
np.newaxis可以只会结论,不需要知道为什么
根据训练的决策树预测结果
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
plt.figure() # 新建画布
plt.scatter(X, y, s=20, edgecolor='black', c='darkorange', label='data')
plt.plot(X_test, y_1, color='cornflowerblue', label='max_depth=2', linewidth=2) # 画线
plt.plot(X_test, y_2, color='yellowgreen', label='max_depth=5', linewidth=2)
plt.xlabel('data')
plt.ylabel('target')
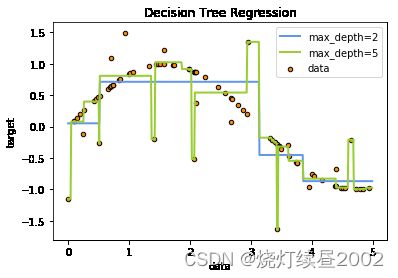
plt.title('Decision Tree Regression')
plt.legend()
plt.show()
显然最大深度等于5的受噪声影响大,有过拟合的趋势