最小二乘算法原理、来源及其Matlab实现(直线拟合)
最小二乘法主要用于解决函数模型最优解问题,是测量工作及其他科学工程领域中,应用最早也是最广泛的算法。
在生产实践中,经常会遇到利用一组观测数据来估计某些未知参数的问题。
举个栗子,
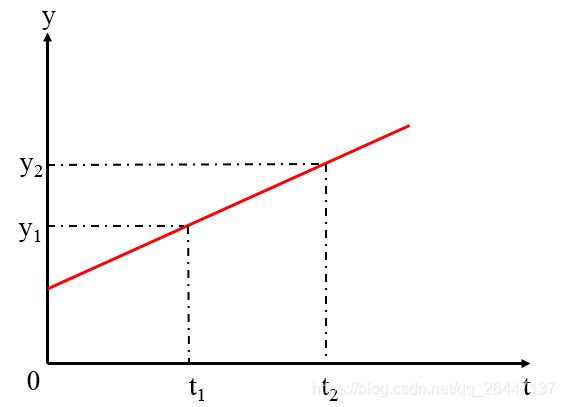
一个做匀速运动的质点在时刻 t 的位置是 y,则可以用如下的线性函数来描述:
y = at + b
其中,a是平均速度,b为质点在 t=0 时刻的初始位置,求参数 a 和 b。
理想情况下,只需要在两个不同时刻 t1 和 t2 观测出质点的相应位置 y1 和 y2,建立两个方程,即可解出两个未知数。这也是我们高中以前常做的、有唯一确定解的问题。
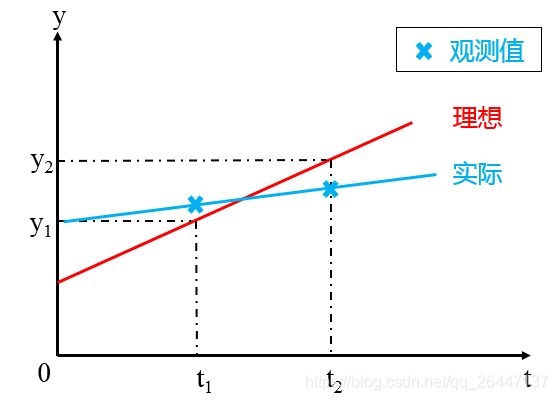
但是,实际观测时,观测值中是带有观测误差(偶然误差、系统误差和粗差)的。
观测误差产生的原因有很多,概括起来有三个方面:
1. 测量仪器
每种仪器只具有一定限度的准确度,比如我们常用的塑料尺,因为只能读到毫米位,毫米以下需要估读,另外,塑料尺因为制造工艺限制,很难保证刻度准确无误,由此观测所得的数据必然带有误差。
2. 观测者
每个人的感官及技术水平、工作态度会有一定差异,所以观测的结果也会有一些差异。
3. 外界条件
测量时所处的外界条件,比如温度、湿度、风力等,都会对观测值直接产生影响。
如果还是像理想情况一样,观测两次,解方程,由于存在误差,得到的结果可能会有很大偏差。
所以,在实际观测时,考虑到观测值带有偶然误差,总是作多余观测。
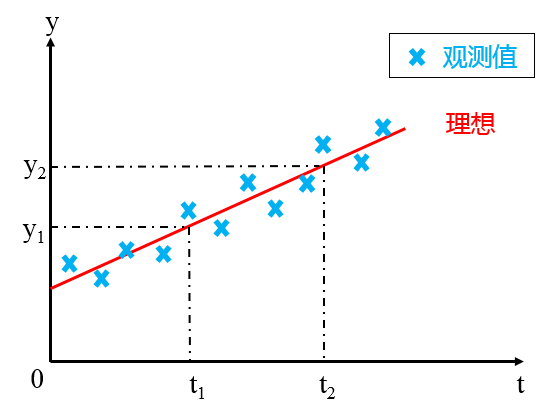
在这种情况下,为了求得 a 和 b,就需要在不同时刻(t1, t2,……tn)来测定其位置,得出一组观测值(y1, y2, ……yn)。这时,由式 y = at + b 可以得到:
ti、yi 为第 i 次观测值, vi 即第 i 次观测时的观测误差。
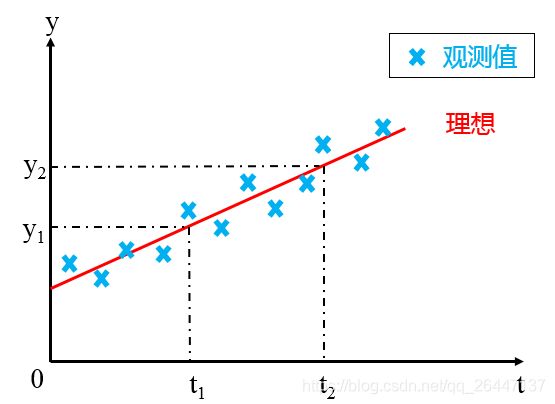
从图中可以看出,由于存在观测误差,由观测数据绘出的点——观测点,描绘不成直线,而有一些“波动”。若将这些观测数据代入方程求解,a 和 b 之值无确定解。
这里就产生这样一个问题:用什么准则来对参数a和b进行估计,从而使估计直线 y = at + b “最佳”地拟合于各观测点?
这里的“最佳”一词可以有不同的理解。例如,可以认为:各观测点对直线最大距离取最小值时,直线是“最佳”的;也可以认为,各观测点到直线的偏差的绝对值之和取最小值时,直线是“最佳”的,等等。在不同的“最佳”要求下,可以求得相应问题中参数a和b不同的估值。
但是,在解这类问题时,一般应用的是最小二乘原理。
最小二乘法最早出现在勒让德1805年发表的论著《计算彗星轨道的新方法》附录中。在此之前,前人多设法构造k个方程去求解,而勒让德没有因袭前人思想。他认为:“赋予误差的平方和为极小,则意味着在这些误差间建立了一种均衡性,它阻止了极端情形所施加的过分影响。这非常好地适用于揭示最接近真实情形的系统状态。”
该附录占据了这本80页小册子的最后9页,在前面关于卫星轨道计算的讨论中没有涉及最小二乘法,可以推测他当时感到这一方法尚不成熟。
到此为止,这个方法仍有其不足之处,即它纯是一个计算方法,缺少误差分析。我们不知道,使用这个方法引起的误差如何,因此也就无法知道,除了若干表面上的优点(例如计算上方便)之外,最小二乘法还有何深层次的优点。要研究这些问题,就需建立一种误差分析理论。
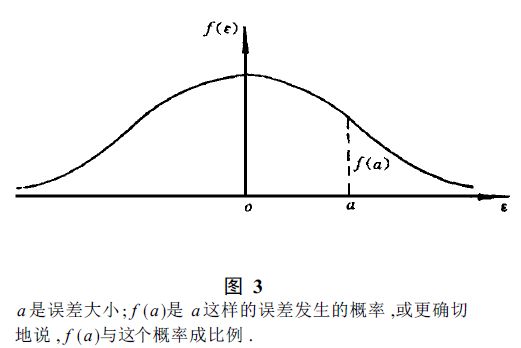
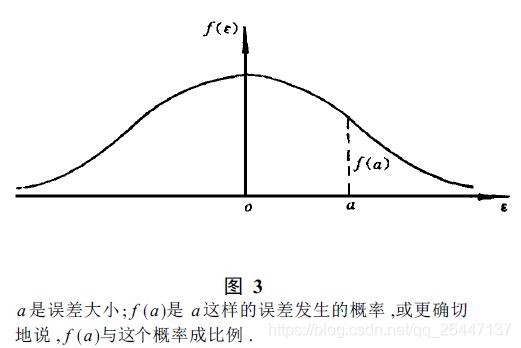
1809年,高斯发表论著《天体运动理论》。在该书末尾,他写了一节有关“数据结合”的问题,以极其简单的手法导出误差分布——正态分布(描述偶然误差通常用正态分布,其特性:在一定观测条件下,误差的绝对值有一定的限制,或者说,超出一定限制的误差,其出现的概率为零;绝对值较小的误差比绝对值较大的误差出现的概率大;绝对值相等的正负误差出现的概率相同;偶然误差的数学期望为零),并用最小二乘法加以验证。
高斯较之于勒让德把最小二乘法推进得更远,他由误差函数推导出这个方法并详尽阐述了最小二乘法的理论依据。可以说,没有高斯的正态误差理论配合,最小二乘法的意义和重要性可能还不到其现今所具有的十分之一。最小二乘方法与高斯误差理论的结合,是数理统计史上最重大的成就之一,其影响直到今日也尚未过时。
关于最小二乘法,高斯宣称自1795年以来他一直使用这个原理。这立刻引起了勒让德的强烈反击,他提醒说科学发现的优先权只能以出版物确定, 并严斥高斯剽窃了他人的发明他们间的争执延续了多年。因而,这两位数学家之间关于优先权的争论,在数学史上的知名度仅次于牛顿和莱布尼兹之间关于微积分发明权的争论。现在一般认为,二人各自独立地发明了最小二乘法,尽管早在10年前,高斯就使用这个原理,但第一个用文字形式发表的是勒让德。
勒让德和高斯发现最小二乘法是从不同的角度入手的:一个是为解线性方程组,一个是寻找误差函数;一个用的是整体思维,考虑方程组的均衡性,一个用的是逆向思维,首先接受经验事实;一个是纯代数方法,一个致力于应用。
再回到开头的问题。
按照最小二乘原理的要求,认为“最佳”地拟合于各观测点的估计曲线,应使各观测点到该曲线的偏差的平方和达到最小。
就是要在满足
的条件下解出参数的估值 a 和 b。
也即测量平差中:
我们用Matlab来实现开头的例子。
clear all
% 生成离散点
t = [0 1 2 3 4 5 6 7 8 9];
y = [0 2 4 7 8 9 12 14 15 18];
% 构造参数矩阵
A = ones(10,2);
A(:,2) = t';
% 参数初值
a = 0; %平均速度
b = 0; %初始位置
% 误差值
l = y - (b + a*t);
% 采用间接平差算法
for i = 1:10
dX = inv(A'*A)*A'*l';
% 更新参数
b = b + dX(1);
a = a + dX(2);
l = y - (b + a*t);
end
% 成图,红色‘+’为生成的离散点,黑色直线为最小二乘拟合直线
plot(t,y,'r+',t,b+a*t,'k')佚名. 误差理论与测量平差基础[M]. 2009.
陈希孺. 最小二乘法的历史回顾与现状[J]. 中国科学院大学学报, 1998(1):4-11.
贾小勇, 徐传胜, 白欣. 最小二乘法的创立及其思想方法[J]. 西北大学学报:自然科学版, 2006, 36(3):507-511.