视觉注意力机制——SENet、CBAM、SKNet

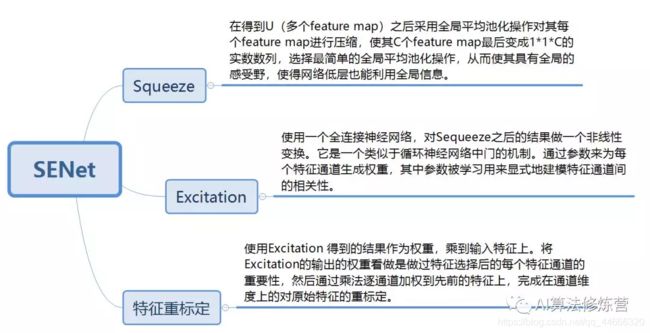
注意力机制(Attentional Mechanism)

通常将软注意力机制中的模型结构分为三大注意力域来分析：

1. 空间域
   空间域——将图片中的的空间域信息做对应的空间变换，从而能将关键的信息提取出来。对空间进行掩码的生成，进行打分，代表是Spatial Attention Module。
2. 通道域
   通道域——类似于给每个通道上的信号都增加一个权重，来代表该通道与关键信息的相关度的话，这个权重越大，则表示相关度越高。对通道生成掩码mask，进行打分，代表是senet, Channel Attention Module。
3. 混合域
   混合域——空间域的注意力是忽略了通道域中的信息，将每个通道中的图片特征同等处理，这种做法会将空间域变换方法局限在原始图片特征提取阶段，应用在神经网络层其他层的可解释性不强。
   而通道域的注意力是对一个通道内的信息直接全局平均池化，而忽略每一个通道内的局部信息，这种做法其实也是比较暴力的行为。所以结合两种思路，就可以设计出混合域的注意力机制模型。同时对通道注意力和空间注意力进行评价打分，代表的有BAM, CBAM。

1. Squeeze-and-Excitation Networks（SENet）–2017

论文地址：https://arxiv.org/abs/1709.01507
代码地址：https://github.com/hujie-frank/SENet

SENet是Squeeze-and-Excitation Networks的简称，由Momenta公司所作并发于2017CVPR，论文中的SENet赢得了ImageNet最后一届**（ImageNet 2017）的图像识别冠军**，论文的核心点在对CNN中的feature channel（特征通道依赖性）利用和创新。提出的SE模块思想简单，易于实现，并且很容易可以加载到现有的网络模型框架中。SENet主要是通过显式地建模通道之间的相互依赖关系，自适应地重新校准通道的特征响应，换句话说，就是学习了通道之间的相关性，筛选出了针对通道的注意力，整个网络稍微增加了一点计算量，但是效果比较好。

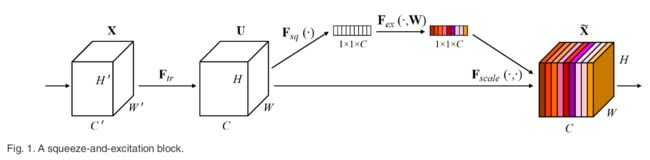
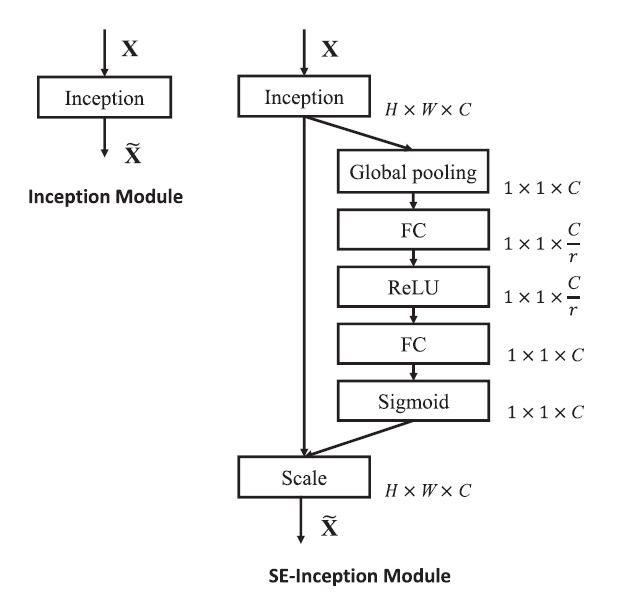
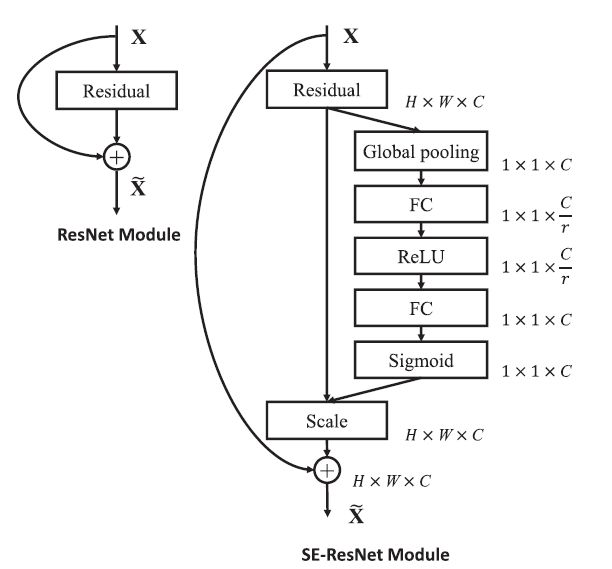
上图是SENet的Block单元，图中的$F_{tr}$是传统的卷积结构，X和U是$F_{tr}$的输入（$C’$x$H’$x$W’$）和输出（$C$x$H$x$W$），这些都是以往结构中已存在的。

SENet增加的部分是U后的结构：对U先做一个Global Average Pooling（图中的$F_{sq}(.)$，作者称为Squeeze过程），输出的1x1xC数据再经过两级全连接（图中的$F_{ex}(.)$，作者称为Excitation过程），最后用sigmoid（论文中的self-gating mechanism）限制到[0，1]的范围，把这个值作为scale乘到U的C个通道上， 作为下一级的输入数据。

这种结构的原理是想通过控制scale的大小，把重要的特征增强，不重要的特征减弱，从而让提取的特征指向性更强。

通俗的说就是：通过对卷积得到的feature map进行处理，得到一个和通道数一样的一维向量作为每个通道的评价分数，然后将改分数分别施加到对应的通道上，得到其结果，就在原有的基础上只添加了一个模块。在这里插入图片描述这是文中给出的一个嵌入Inception结构的一个例子。由（$HWC$）全局平均池化得到（11C），即S步；接着利用两个全连接层和相应的激活函数建模通道之间的相关性，即E步。E步中包含参数r的目的是为了减少全连接层的参数。输出特征通道的权重通过乘法逐通道加权到原来的特征上，得到（HWC）的数据，与输入形状完全相同。

基于Pytorch的代码实现：

class SELayer(nn.Module):
	def __init__(self, channel, reduction=16):
		super(SELayer, self).__init__()
		# 前后通道数不发生改变
		self.avg_pool = nn.AdaptiveAvgPool2d(1)
		self.fc = nn.Sequential(
			nn.Linear(channel, channel // reduction, bias=False),
			nn.ReLu(inplace=True),
			nn.Linear(channel // reduction, channel, bias=False),
			nn.Sigmoid()
		)

	def forward(self, x):
		b, c, _, _ = x.size()
		y = self.avg_pool(x).view(b, c)
		y = self.fc(y).view(b, c, 1, 1)
		# 将张量扩展为参数x的大小。
		return x * y.expand_as(x)

2. Convolutional Block Attention Module（CBAM）–2018

论文地址http://openaccess.thecvf.com/content_ECCV_2018/papers/Sanghyun_Woo_Convolutional_Block_Attention_ECCV_2018_paper.pdf

在该论文中，作者研究了网络架构中的注意力，注意力不仅要告诉我们重点关注哪里，还要提高关注点的表示。目标是通过使用注意机制来增加表现力，关注重要特征并抑制不必要的特征。为了强调空间和通道这两个维度上的有意义特征，作者依次应用通道和空间注意模块，来分别在通道和空间维度上学习关注什么、在哪里关注。此外，通过了解要强调或抑制的信息也有助于网络内的信息流动。

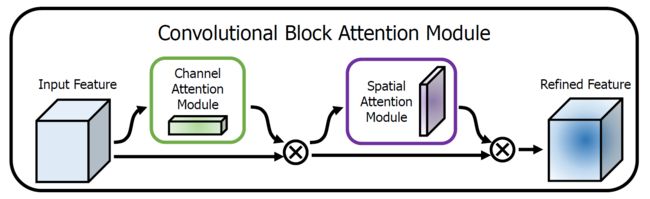
上图为整个CBAM的示意图，先是通过注意力机制模块，然后是空间注意力模块，对于两个模块先后顺序对模型性能的影响，本文作者也给出了实验的数据对比，先通道再空间要比先空间再通道以及通道和空间注意力模块并行的方式效果要略胜一筹。

那么这个通道注意力模块和空间注意力模块又是如何实现的呢？

通道注意力模块

这个部分大体上和SENet的注意力模块相同，主要的区别是CBAM在S步采取了全局平均池化以及全局最大池化，两种不同的池化意味着提取的高层次特征更加丰富。接着在E步同样通过两个全连接层和相应的激活函数建模通道之间的相关性，合并两个输出得到各个特征通道的权重。最后，得到特征通道的权重之后，通过乘法逐通道加权到原来的特征上，完成在通道维度上的原始特征重标定。

PyTorch实现

class ChannelAttention(nn.Module):
	def __init__(self, in_planes, ratio=16):
		super(ChannelAttention, self).__init__()
		self.avg_pool = nn.AdaptiveAvgPool2d(1)
		self.max_pool = nn.AdaptiveMaxPool2d(1)

		self.shareMLP = nn.Sequential(
			nn.Conv2d(in_planes, in_planes // ratio, 1, bias=False),
			nn.ReLU(),
			nn.Conv2d(in_planes // ratio, in_planes, 1, bias=False)
		)
		self.sigmoid = nn.Sigmoid()

	def forward(self, x):
		avgout = self.shareMLP(self.avg_pool(x))
		maxout = self.shareMLP(self.max_pool(x))
		return self.sigmoid(avgout + maxout)

空间注意力模块

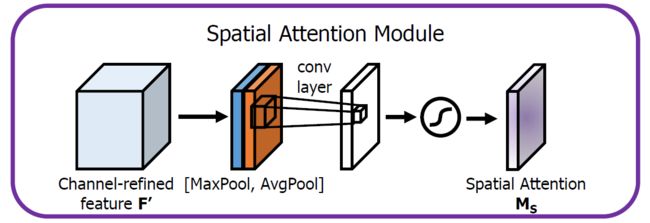
首先输入的是经过通道注意力模块的特征，同样利用了全局平均池化和全局最大池化，不同的是，这里是在通道这个维度上进行的操作，也就是说把所有输入通道池化成2个实数，由（hxwxc）形状的输入得到两个（hxwx1）的特征图。接着使用一个 7x7 的卷积核，卷积后形成新的（hxwx1）的特征图。最后也是相同的Scale操作,注意力模块特征与得到的新特征图相乘得到经过双重注意力调整的特征图。

PyTorch实现

基于ResNet实现

class SpatialAttention(nn.Module):
	def __init__(self, kernel_size=7):
		super(SpatialAttention, self).__init__()
		assert kernel_size in (3, 7), "kernel size must be 3 or 7"
		padding = 3 if kernel_size == 7 else 1

		self.conv = nn.Conv2d(2, 1, kernel_size, padding=padding, bias=False)
		self.sigmoid = nn.Sigmoid()
	
	def forward(self, x):
	# 沿着通道取平均
		avgout = torch.mean(x, dim=1, keepdim=True)
		maxout, _ = torch.max(x, dim=1, keepdim=True)
		x = torch.cat([avgout, maxout], dim=1)
		x = self.conv(x)
		return self.sigmoid(x)

网络整体代码：

class BasicBlock(nn.Module):
	expansion = 1
	def __init__(self, in_planes, planes, stride=1, downsample=None):
		super(BasicBlock, self).__init__()
		self.conv1 = conv3x3(in_planes, planes, stride);
		self.bn1 = nn.BatchNorm2d(planes)
		self.relu = nn.ReLU(inplace=True)
		self.conv2 = conv3x3(planes, planes)
		self.bn2 = nn.BatchNorm2d(planes)
		self.ca = ChannelAttention(planes)
		self.sa = SpatialAttention()
		self.downsample = downsample
		self.stride = stride

	def forward(self, x):
		residual = x
		out = self.conv1(x)
		out = self.bn1(out)
		out = self.relu(out)
		out = self.conv2(out)
		out = self.bn2(out)
		out = self.relu(out)
		out = self.ca(out) * out # 广播机制
		out = self.sa(out) * out # 广播机制
		if self.downsample is not None:
			residual = self.downsample(x)
		out += residual
		return out

3. Selective Kernel Networks（SKNet）–2019

论文地址：https://arxiv.org/abs/1903.06586
代码地址：https://github.com/implus/SKNet

Selective Kernel Networks（SKNet）发表在CVPR 2019，是对Momenta发表于CVPR 2018上论文SENet的改进，且这篇的作者中也有Momenta的同学参与。

SENet是对特征图的通道注意力机制的研究，之前的CBAM提到了对特征图空间注意力机制的研究。这里SKNet针对卷积核的注意力机制研究。

在该模块中，作者使用了多分支卷积网络、组卷积、空洞卷积以及注意力机制。

多分支卷积网络

多分支卷积网络，如字面意思，含有多于一个分支的卷积网络，下图所示的网络模块均属于多分支卷积网络。

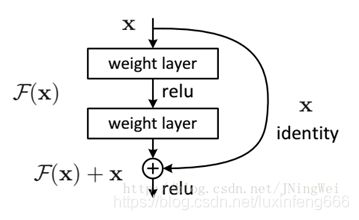
该模块是经典的残差网络模块，使用了双分支结构，跨层连接的那条分支是一条单纯的恒等映射分支。

该模块是Inception模块，也是一个多分支卷积网络，与残差网络的多分支不同的是，该模块的每个分支都进行了卷积处理，并不是一个恒等映射。

分组卷积（Group convolution）


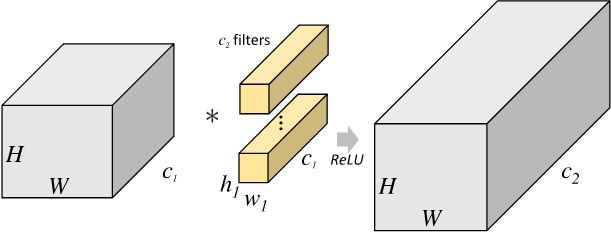
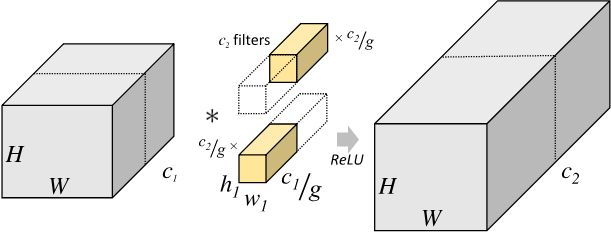
第一张图代表标准卷积操作。若输入特征图尺寸为 $H\times W\times c1$，卷积核尺寸为 $h1\times w1\times c2$ ，输出特征图尺寸为$H\times W\times c2$ ，标准卷积层的参数量为：$h1\times w1\times c1\times c2$ 。（一个滤波器在输入特征图 ($h1\times w1\times c1)\times c2$ 大小的区域内操作，输出结果为1个数值，所以需要 $c2$ 个滤波器。）

第二张图代表分组卷积操作。将输入特征图按照通道数分成 $G$ 组，则每组输入特征图的尺寸为 $H\times W\times \frac{(c1)}{g}$ ，对应的卷积核尺寸为 $H\times W\times \frac{(c1)}{g}$ ，每组输出特征图尺寸为 $H\times W\times \frac{(c2)}{g}$。将 $g$ 组结果拼接(concat)，得到最终尺寸为 $H\times W\times c2$ 的输出特征图。分组卷积层的参数量为$H\times W\times \frac{(c1)}{g}\times \frac{(c2)}{g}\times g$ = $H\times W\times \frac{(c1c2)}{g}$。

深入思考一下，常规卷积输出的特征图上，每一个点是由输入特征图 $H\times W\times c1$ 个点计算得到的；而分组卷积输出的特征图上，每一个点是由输入特征图 $H\times W\times \frac{(c1)}{g}$ 个点计算得到的。自然，分组卷积的参数量是标准卷积的 $\frac{1}{g}$ 。

注：分组卷积在ResNeXt网络中进行了使用，实现了不错的检测效果精度，有兴趣的同学可以看看哦。

空洞卷积
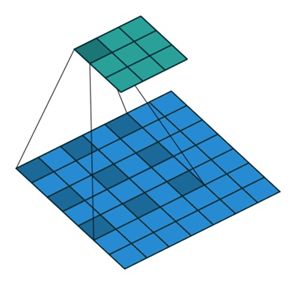
空洞卷积与标准卷积相比，增大了感受野。一般情况下，卷积之后的池化操作缩小feature map的尺寸也能达到增加感受野的效果，但是池化过程会导致信息的丢失，所以引入了空洞卷积操作。下图为Dilation=2时的卷积效果图，当Dilation=2时，3×3的卷积核的感受野为5×5。空洞卷积与标准卷积相比，在不增加参数量的同时增大了感受野。

注意力机制
参考SENet

不同大小的感受视野（卷积核）对于不同尺度（远近、大小）的目标会有不同的效果。尽管比如Inception这样的增加了多个卷积核来适应不同尺度图像，但是一旦训练完成后，参数就固定了，这样多尺度信息就会被全部使用了（每个卷积核的权重相同）。


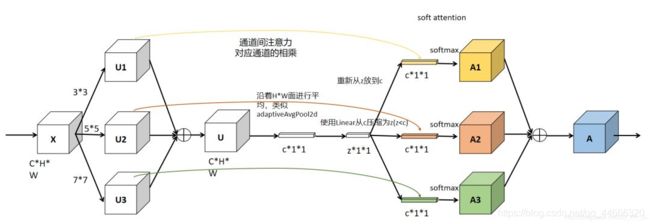
此图为GiantPandaCV公众号作者根据代码重画的网络图
网络主要由Split、Fuse、Select三部分组成。

1.Split部分是对原特征图经过不同大小的卷积核部分进行卷积的过程，这里可以有多个分支

对输入X使用不同大小卷积核分别进行卷积操作（图中的卷积核size分别为3x3和5x5两个分支，但是可以有多个分支）。操作包括卷积、efficient grouped/depthwise convolutions、BN。

2.Fuse部分是计算每个卷积核权重的部分。

将两部分的特征图按元素求和

U通过全局平均池化（GAP）生成通道统计信息。得到的Sc维度为C * 1

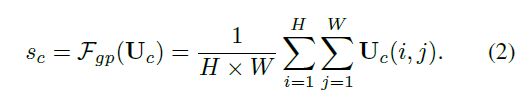
经过全连接生成紧凑的特征z（维度为d * 1）， δ是RELU激活函数，B表示批标准化（BN），z的维度为卷积核的个数，W维度为d×C， d代表全连接后的特征维度，L在文中的值为32，r为压缩因子。

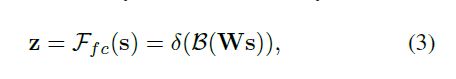
3.Select部分是根据不同权重卷积核计算后得到的新的特征图的过程。

进行softmax计算每个卷积核的权重，计算方式如下图所示。如果是两个卷积核，则 $ac+bc=1$。z的维度为$（d\ast 1）$，A的维度为$（C\ast d）$，B的维度为$（C\ast d）$，则$a=A$ $xz$的维度为$1\ast C$。

$A_c$、$B_c$为$A$、$B$的第$c$行数据$（1\ast d）$。$ac$为$a$的第$c$个元素，这样分别得到了每个卷积核的权重。

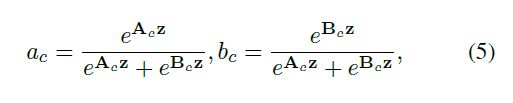
将权重应用到特征图上。其中$V=[V1,V2,\dots ,VC]$, $V_c$ 维度为$（HxW）$，如果select中softmax部分可参考下图（3个卷积核）

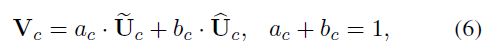
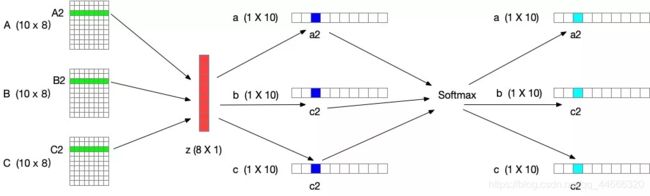
下图是针对SKNet总结的思维导图，参考地址：https://blog.csdn.net/qq_34784753/article/details/89381947?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task

PyTorch实现

class SKConv(nn.Module):
    def __init__(self, features, WH, M, G, r, stride=1, L=32):
        super(SKConv, self).__init__()
        # z的通道数
        d = max(int(features / r), L)
        self.M = M
        self.features = features
        self.convs = nn.ModuleList([])
        for i in range(M):
            # 使用不同kernel size的卷积
            self.convs.append(
                nn.Sequential(
                    nn.Conv2d(features,
                              features,
                              kernel_size=3 + i * 2,
                              stride=stride,
                              padding=1 + i,
                              groups=G), nn.BatchNorm2d(features),
                    nn.ReLU(inplace=False)))
            
        self.fc = nn.Linear(features, d)
        self.fcs = nn.ModuleList([])
        for i in range(M):
            self.fcs.append(nn.Linear(d, features))
        self.softmax = nn.Softmax(dim=1)

    def forward(self, x):
        for i, conv in enumerate(self.convs):
            fea = conv(x).unsqueeze_(dim=1)
            if i == 0:
                feas = fea
            else:
                feas = torch.cat([feas, fea], dim=1)
        fea_U = torch.sum(feas, dim=1)
        fea_s = fea_U.mean(-1).mean(-1)
        fea_z = self.fc(fea_s)
        for i, fc in enumerate(self.fcs):
            print(i, fea_z.shape)
            vector = fc(fea_z).unsqueeze_(dim=1)
            print(i, vector.shape)
            if i == 0:
                attention_vectors = vector
            else:
                attention_vectors = torch.cat([attention_vectors, vector],
                                              dim=1)
        attention_vectors = self.softmax(attention_vectors)
        attention_vectors = attention_vectors.unsqueeze(-1).unsqueeze(-1)
        fea_v = (feas * attention_vectors).sum(dim=1)
        return fea_v	

参考：
1.https://blog.csdn.net/xjz18298268521/article/details/79078551

2.https://blog.csdn.net/qq_28454857/article/details/88837601

3.https://zhuanlan.zhihu.com/p/59690223

4.https://blog.csdn.net/qq_39027890/article/details/86656182