基于猎人猎物优化算法的函数寻优算法

一、理论基础

1、猎人猎物优化算法

本文提出了一种新的基于种群的优化算法—猎人猎物优化算法(Hunter–prey optimizer, HPO)。该算法的灵感来源于狮子、豹子和狼等食肉动物，以及鹿和羚羊等猎物的行为。
所有优化算法的总体结构基本相同。首先，将初始总体随机设置为$(x)=\{x_1,x_2,\cdots ,x_n\}$，然后将种群总体所有成员的目标函数计算为$(O)=\{O_1,O_2,\cdots ,O_n\}$。受该算法启发，通过一系列规则和策略在搜索空间中控制和引导种群。重复此过程，直到算法停止。 在每次迭代中，根据该算法的规则更新群体中每个成员的位置，并用目标函数评估新位置，这个过程会使解决方案随着每次迭代而优化。初始群体中每个成员的位置由式(1)在搜索空间中随机生成。$$x_i=rand(1,d).\ast (ub-lb)+lb\text{\hspace{1em}(1)}$$其中，$x_i$是猎人或猎物的位置，$lb$是问题变量的最小值(下界)，$ub$是问题变量的最大值(上界)，$d$是问题变量的数量(维度)。式(2)定义了搜索空间的下界和上界。需要注意的是，一个问题的所有变量的上下限可能相同或不同。$$lb=[l{b}_1,l{b}_2,\cdots ,l{b}_d],ub=[u{b}_1,u{b}_2,\cdots ,u{b}_d]\text{\hspace{1em}(2)}$$生成初始总体并确定每个代理的位置后，使用目标函数$O_i=f(x)$计算每个解的适应度值。$F(x)$可以是最大值(效率、性能等)或最小值(成本、时间等)。搜索机制通常包括两个步骤：探索和开发。探索是指算法倾向于高度随机的行为，因此解决方案会发生显著变化。解决方案的重大变化促使猎人进一步探索搜索空间，并发现其有希望的领域。在发现有希望的区域后，必须减少随机行为，以便算法能够在有希望的区域周围搜索，这就是开发。
对于猎人的搜索机制，式(3)给出了其数学模型：$$x_{i,j}(t+1)=x_{i,j}(t)+0.5\left[(2CZ{P}_{pos(j)}-x_{i,j}(t))+(2(1-C)Z\mu (j)-x_{i,j}(t))\right]\text{\hspace{1em}(3)}$$其中，$x(t)$是当前猎人位置，$x(t+1)$是猎人的下一次迭代位置，$P_{pos}$是猎物的位置，$\mu$是所有位置的平均值，$Z$是由式(4)计算的自适应参数：$$\begin{array}{l}P=R_1<C;IDX=(P==0);\\ Z=R_2\otimes IDX+R_3\otimes (\sim IDX)\end{array}\text{\hspace{1em}(4)}$$其中，$R_1$和$R_3$是$[0,1]$内的随机向量，$P$是$R_1<C$的索引值，$R_2$是$[0,1]$内的随机数，$IDX$是满足条件($P==0$)的向量$R_1$的索引值，$C$是探索和开发之间的平衡参数，其值在迭代过程中从1减小到0.02，计算如下：$$C=1-it\left(\frac{0.98}{MaxIt}\right)\text{\hspace{1em}(5)}$$其中，$it$是当前迭代次数，$MaxIt$是最大迭代次数。计算猎物的位置($P_{pos}$)，以便首先根据式(6)计算所有位置的平均值($\mu$)，然后计算每个搜索代理与该平均位置的距离。$$\mu =\frac{1}{n}\sum _{i=1}^n{x}_i\text{\hspace{1em}(6)}$$根据式(7)计算欧几里得距离：$$D_{euc(i)}={\left(\sum _{j=1}^d(x_{i,j}-{\mu }_j{)}^2\right)}^{\frac{1}{2}}\text{\hspace{1em}(7)}$$根据式(8)，距离位置平均值最大的搜索代理被视为猎物($P_{pos}$)：$$P_{pos}=x_i|iisindexofMax(end)sort(D_{euc})\text{\hspace{1em}(8)}$$如果每次迭代都考虑到搜索代理与平均位置($\mu$)之间的最大距离，则该算法将具有延迟收敛性。根据狩猎场景，当猎人捕获猎物时，猎物会死亡，而下一次，猎人会移动到新的猎物位置。为了解决这个问题，考虑一种递减机制，如式(9)所示：$$kbest=round(C\times N)\text{\hspace{1em}(9)}$$其中$N$是搜索代理的数量。
改变式(8)，将猎物的位置计算为式(10)：$$P_{pos}=x_i|iissorted{D}_{euc}(kbest)\text{\hspace{1em}(10)}$$在算法开始时，$kbest$的值等于$N$。因此，最后一个距离搜索代理的平均位置($\mu$)最远的搜索代理被选择为猎物，并被猎人捕获。
假设最佳安全位置是最佳全局位置，因为这将使猎物有更好的生存机会，猎人可能会选择另一个猎物。式(11)用于更新猎物位置：$$x_{i,j}(t+1)=T_{pos(j)}+CZ\cos (2\pi R_4)\times (T_{pos(j)}-x_{i,j}(t))\text{\hspace{1em}(11)}$$其中，$x(t)$是猎物的当前位置；$x(t+1)$是猎物的下一次迭代位置；$T_{pos}$是全局最优位置；$Z$是由式(4)计算的自适应参数；$R_4$是范围$[-1,1]$内的随机数；$C$是探索和开发之间的平衡参数，其值在算法的迭代过程中减小，并由式(5)计算；$\cos$函数及其输入参数允许下一个猎物位置在不同半径和角度的全局最优位置，并提高开发阶段的性能。
为了选择猎人和猎物，结合式(3)和(11)提出了式(12)：$$x_i(t+1)=\{\begin{array}{l}{x}_i(t)+0.5\left[(2CZ{P}_{pos(j)}-x_i(t))+(2(1-C)Z\mu (j)-x_i(t))\right]if{R}_5<\beta (12a)\\ T_{pos}+CZ\cos (2\pi R_4)\times (T_{pos}-x_i(t))else(12b)\end{array}\text{\hspace{1em}(12)}$$其中，$R_5$是$[0,1]$范围内的随机数，$\beta$是一个调节参数，在本文中的值设置为0.1。如果$R_5$值小于$\beta$，搜索代理将被视为猎人，搜索代理的下一个位置将用式(12a)更新；如果$R_5$值大于$\beta$，搜索代理将被视为猎物，搜索代理的下一个位置将用式(12b)更新。

2、HPO算法流程图

所提出算法的流程图如图1所示。

图1 HPO算法流程图

二、仿真实验与结果分析

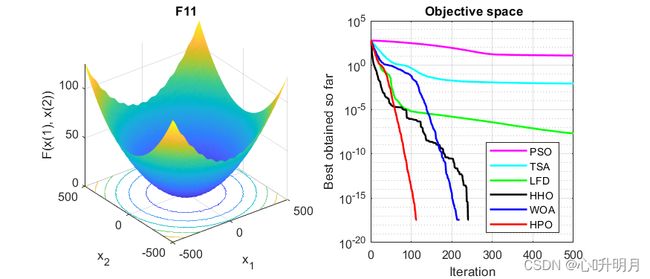
将HPO与PSO、TSA、LFD、HHO和WOA进行对比，实验设置种群规模为30，最大迭代次数为500，每种算法独立运行30次，以文献[1]中30维的F3、F4、F5(单峰函数)、F10、F11、F12(多峰函数)为例，结果显示如下：

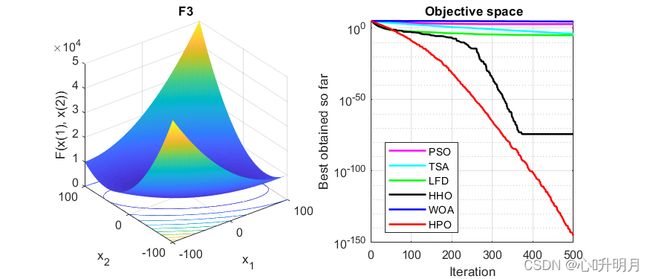
函数：F3
PSO：最差值: 1655.3088, 最优值: 144.4169, 平均值: 705.5008, 标准差: 374.0712, 秩和检验: 3.0199e-11
TSA：最差值: 0.0014177, 最优值: 6.3681e-09, 平均值: 0.00010689, 标准差: 0.00027107, 秩和检验: 3.0199e-11
LFD：最差值: 2.7324e-05, 最优值: 1.609e-06, 平均值: 1.0413e-05, 标准差: 6.5274e-06, 秩和检验: 3.0199e-11
HHO：最差值: 1.9747e-73, 最优值: 7.5816e-97, 平均值: 7.3121e-75, 标准差: 3.6064e-74, 秩和检验: 3.0199e-11
WOA：最差值: 77911.2649, 最优值: 22160.2961, 平均值: 49304.8815, 标准差: 13888.0351, 秩和检验: 3.0199e-11
HPO：最差值: 2.125e-144, 最优值: 4.8337e-159, 平均值: 7.0978e-146, 标准差: 3.8795e-145, 秩和检验: 1
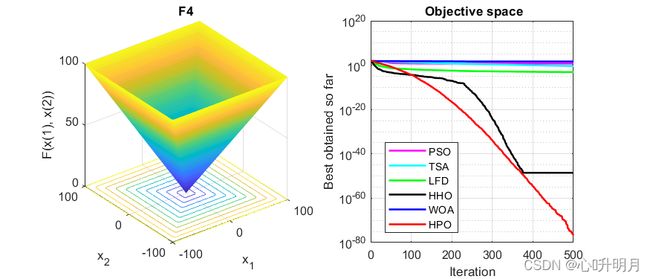
函数：F4
PSO：最差值: 9.2222, 最优值: 2.6354, 平均值: 5.5985, 标准差: 1.7375, 秩和检验: 3.0199e-11
TSA：最差值: 1.5538, 最优值: 0.018393, 平均值: 0.3713, 标准差: 0.3628, 秩和检验: 3.0199e-11
LFD：最差值: 0.0011982, 最优值: 0.00037569, 平均值: 0.00076243, 标准差: 0.00022244, 秩和检验: 3.0199e-11
HHO：最差值: 4.1015e-48, 最优值: 2.2482e-64, 平均值: 2.8774e-49, 标准差: 8.865e-49, 秩和检验: 3.0199e-11
WOA：最差值: 90.8896, 最优值: 0.63375, 平均值: 48.1807, 标准差: 25.9539, 秩和检验: 3.0199e-11
HPO：最差值: 1.9138e-76, 最优值: 4.679e-83, 平均值: 2.0117e-77, 标准差: 5.0094e-77, 秩和检验: 1
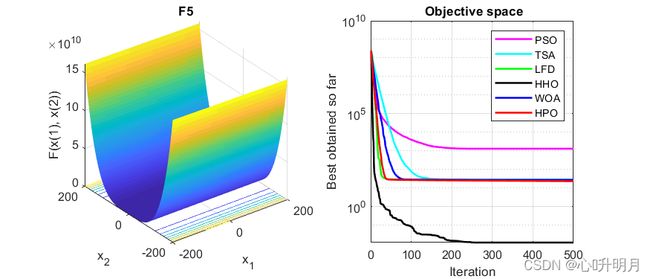
函数：F5
PSO：最差值: 3265.9273, 最优值: 395.2169, 平均值: 1310.819, 标准差: 709.752, 秩和检验: 3.0199e-11
TSA：最差值: 32.6867, 最优值: 26.4304, 平均值: 28.5989, 标准差: 0.98266, 秩和检验: 3.0199e-11
LFD：最差值: 28.2876, 最优值: 27.6816, 平均值: 28.0259, 标准差: 0.1791, 秩和检验: 3.0199e-11
HHO：最差值: 0.046694, 最优值: 2.1425e-05, 平均值: 0.011778, 标准差: 0.013516, 秩和检验: 3.0199e-11
WOA：最差值: 28.7441, 最优值: 27.1566, 平均值: 27.9145, 标准差: 0.45396, 秩和检验: 3.0199e-11
HPO：最差值: 26.0057, 最优值: 23.1074, 平均值: 23.6597, 标准差: 0.56852, 秩和检验: 1
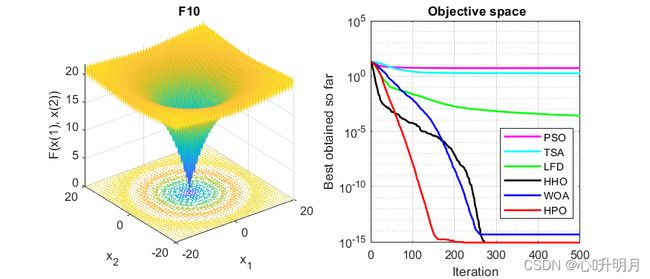
函数：F10
PSO：最差值: 8.7096, 最优值: 3.4325, 平均值: 5.3647, 标准差: 1.0923, 秩和检验: 1.2118e-12
TSA：最差值: 3.4079, 最优值: 1.8519e-12, 平均值: 1.8109, 标准差: 1.5196, 秩和检验: 1.2118e-12
LFD：最差值: 0.00036925, 最优值: 0.00017272, 平均值: 0.00026293, 标准差: 5.3357e-05, 秩和检验: 1.2118e-12
HHO：最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
WOA：最差值: 7.9936e-15, 最优值: 8.8818e-16, 平均值: 4.7962e-15, 标准差: 2.8529e-15, 秩和检验: 1.2954e-08
HPO：最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
函数：F11
PSO：最差值: 24.4352, 最优值: 4.6305, 平均值: 12.1824, 标准差: 4.3481, 秩和检验: 1.2118e-12
TSA：最差值: 0.028988, 最优值: 0, 平均值: 0.0084913, 标准差: 0.0095626, 秩和检验: 5.375e-06
LFD：最差值: 8.1923e-08, 最优值: 4.2355e-09, 平均值: 2.0162e-08, 标准差: 1.828e-08, 秩和检验: 1.2118e-12
HHO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
WOA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
HPO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
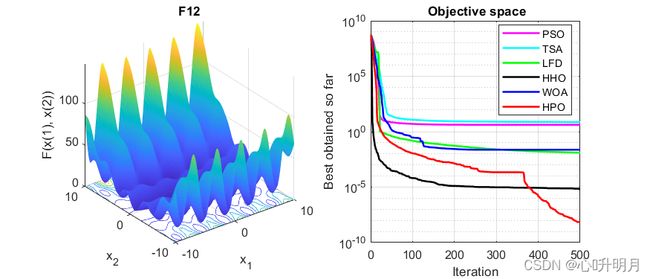
函数：F12
PSO：最差值: 11.6649, 最优值: 1.0804, 平均值: 4.175, 标准差: 2.1919, 秩和检验: 3.0199e-11
TSA：最差值: 13.0908, 最优值: 0.67667, 平均值: 7.3373, 标准差: 3.9204, 秩和检验: 3.0199e-11
LFD：最差值: 0.12132, 最优值: 0.0007559, 平均值: 0.012568, 标准差: 0.028406, 秩和检验: 3.0199e-11
HHO：最差值: 2.7599e-05, 最优值: 3.2155e-09, 平均值: 6.3657e-06, 标准差: 7.7866e-06, 秩和检验: 4.9752e-11
WOA：最差值: 0.065805, 最优值: 0.0065428, 平均值: 0.023731, 标准差: 0.015485, 秩和检验: 3.0199e-11
HPO：最差值: 1.9617e-07, 最优值: 3.1496e-11, 平均值: 6.9024e-09, 标准差: 3.5754e-08, 秩和检验: 1

实验结果表明：所提出的HPO算法对解决单峰和多峰问题具有足够的探索和开发能力，与其他优化算法相比，HPO算法的性能更优越。

三、参考文献

[1] Naruei, I., Keynia, F., Sabbagh Molahosseini, A. Hunter-prey optimization: algorithm and applications[J]. Soft Computing, 2022, 26: 1279-1314.