动手学深度学习Pytorch(二)——线性回归
文章目录
- 1. 基础知识
-
- 1.1 线性模型
- 1.2 模型评估
- 1.3 模型训练
- 1.4 优化方法——梯度下降
-
- 小批量随机梯度下降
- 2. 代码
-
- 2.1 构造人为数据集
- 2.2 构造Pytorch数据迭代器
- 2.3 初始化模型
- 2.4 模型训练
- 代码总结
- 参考资料
1. 基础知识
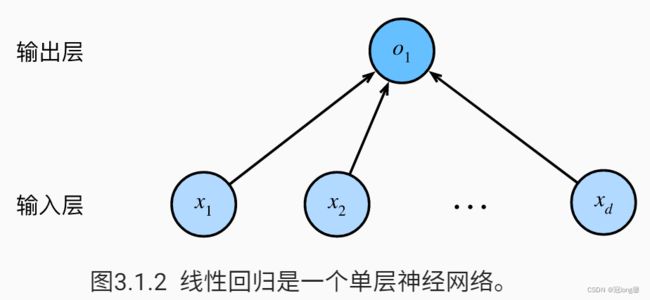
1.1 线性模型
给定n维输入 x = [ x 1 , x 2 , ⋯ , x n ] T x=[x_1,x_2,\cdots,x_n]^T x=[x1,x2,⋯,xn]T,线性模型有一个n维权重 w = [ w 1 , w 2 , ⋯ , w n ] w=[w_1,w_2,\cdots,w_n] w=[w1,w2,⋯,wn]和一个标量偏差b,则模型的输出为:
y = w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b = < w , x > + b y=w_1x_1+w_2x_2+\cdots+w_nx_n+b=
1.2 模型评估
(1)平方损失MSE
假设y是真实值, y ^ \hat{y} y^是估计值,则平方损失为:
ℓ ( y , y ^ ) = 1 2 ( y − y ^ ) 2 \ell(y,\hat{y})=\frac{1}{2}(y-\hat{y})^2 ℓ(y,y^)=21(y−y^)2
1.3 模型训练
假设有n个样本 X = [ x 1 , x 2 , ⋯ , x n ] T , y = [ y 1 , y 2 , ⋯ , y n ] T X=[x_1,x_2,\cdots,x_n]^T,y=[y_1,y_2,\cdots,y_n]^T X=[x1,x2,⋯,xn]T,y=[y1,y2,⋯,yn]T
损失函数
ℓ ( X , y , w , b ) = 1 2 n ∑ i = 1 n ( y i − < x i , w > − b ) 2 = 1 2 n ∥ y − X w − b ∥ 2 \ell(X,y,w,b)=\frac{1}{2n}\sum_{i=1}^n(y_i-
最小化损失函数
w ∗ , b ∗ = arg min w , b ℓ ( X , y , w , b ) w^*,b^*=\arg \min_{w,b} \ell(X,y,w,b) w∗,b∗=argw,bminℓ(X,y,w,b)
最优解
将偏差加入权重: X ← [ X , 1 ] , w ← [ w , b ] T X \leftarrow [X,1],w \leftarrow [w,b]^T X←[X,1],w←[w,b]T
ℓ ( X , y , w ) = 1 2 n ∥ y − X w ∥ 2 ∂ ∂ w ℓ ( X , y , w ) = 1 n ( y − X w ) T X \ell(X,y,w)=\frac{1}{2n} \| y-Xw\|^2 \\ \frac{\partial}{ \partial w}\ell(X,y,w)=\frac{1}{n}(y-Xw)^TX ℓ(X,y,w)=2n1∥y−Xw∥2∂w∂ℓ(X,y,w)=n1(y−Xw)TX
因此最优解满足:
1 n ( y − X w ) T X = 0 w ∗ = ( X T X ) − 1 X T y \frac{1}{n}(y-Xw)^TX=0 \\ w^*=(X^TX)^{-1}X^Ty n1(y−Xw)TX=0w∗=(XTX)−1XTy
线性回归是对n维输入的加权和,外加偏差。线性回归有显示解。
1.4 优化方法——梯度下降
当问题没有显示解时,可以采用梯度下降法
步骤
- 挑选一个初始值 w 0 w_0 w0
- 重复迭代参数 t = 1 , 2 , 3 t=1,2,3 t=1,2,3,更新参数值 w t = w t − 1 − η ∂ ℓ ∂ w t − 1 w_t=w_{t-1}-\eta \frac{\partial \ell}{\partial w_{t-1}} wt=wt−1−η∂wt−1∂ℓ
学习率 η \eta η: 步长的超参数
小批量随机梯度下降
每次计算梯度,都需要对损失函数求导。因为损失函数是对所有样本的平均,所有在整个训练集上算梯度太贵。
我们可以随机采样b个样本 i 1 , i 2 , ⋯ , i b i_1,i_2,\cdots,i_b i1,i2,⋯,ib来近似损失
1 b ∑ ℓ ( x i , y i , w ) \frac{1}{b} \sum \ell(x_i,y_i,w) b1∑ℓ(xi,yi,w)
批量(batch): 损失误差精度的超参数

小批量随机梯度下降是深度学习默认的求解算法。
2. 代码
import imp
import torch
import numpy as np
from torch.utils import data
from d2l import torch as d2l
from torch import nn
2.1 构造人为数据集
# 构造人造数据集
def synthetic_data(w, b, num_examples):
# 生成 y = Xw + b + 噪声
X = torch.normal(0, 1, (num_examples, len(w)))
Y = torch.matmul(X, w) + b
Y += torch.normal(0, 0.01, Y.shape)
return X, Y.reshape((-1,1))
# 构造数据
true_w = torch.tensor([2, -3.4], dtype=torch.float32)
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
2.2 构造Pytorch数据迭代器
# 构造一个Pytorch 数据迭代器
def load_array(data_arrays, batch_size, is_train = True):
dataset = data.TensorDataset(*data_arrays) # 将列表元素分别当作参数传入
return data.DataLoader(dataset, batch_size, shuffle=is_train)
# 获得数据迭代器
batch_size = 10
data_iter = load_array((features, labels), batch_size)
2.3 初始化模型
# 初始化模型
net = nn.Sequential(nn.Linear(2, 1)) # Sequential is a list of layers
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
# 误差计算
loss = nn.MSELoss()
# SGD
trainer = torch.optim.SGD(net.parameters(), lr = 0.03)
2.4 模型训练
num_epochs = 3
for epoch in range(num_epochs):
for X, y in data_iter:
l = loss(net(X), y)
trainer.zero_grad() # 梯度清零
l.backward() # 反向梯度计算
trainer.step() # 模型更新
l = loss(net(features), labels) # loss自动求和
print(f'epoch {epoch + 1}, loss {l:f}')
代码总结
import imp
import torch
import numpy as np
from torch.utils import data
from d2l import torch as d2l
from torch import nn
# 构造人造数据集
def synthetic_data(w, b, num_examples):
# 生成 y = Xw + b + 噪声
X = torch.normal(0, 1, (num_examples, len(w)))
Y = torch.matmul(X, w) + b
Y += torch.normal(0, 0.01, Y.shape)
return X, Y.reshape((-1,1))
# 构造一个Pytorch 数据迭代器
def load_array(data_arrays, batch_size, is_train = True):
dataset = data.TensorDataset(*data_arrays) # 将列表元素分别当作参数传入
return data.DataLoader(dataset, batch_size, shuffle=is_train)
# 构造数据
true_w = torch.tensor([2, -3.4], dtype=torch.float32)
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
# 获得数据迭代器
batch_size = 10
data_iter = load_array((features, labels), batch_size)
# 初始化模型
net = nn.Sequential(nn.Linear(2, 1)) # Sequential is a list of layers
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
# 误差计算
loss = nn.MSELoss()
# SGD
trainer = torch.optim.SGD(net.parameters(), lr = 0.03)
num_epochs = 3
for epoch in range(num_epochs):
for X, y in data_iter:
l = loss(net(X), y)
trainer.zero_grad() # 梯度清零
l.backward() # 反向梯度计算
trainer.step() # 模型更新
l = loss(net(features), labels) # loss自动求和
print(f'epoch {epoch + 1}, loss {l:f}')
epoch 1, loss 0.000175
epoch 2, loss 0.000111
epoch 3, loss 0.000112
参考资料
[1]跟李沐学AI:https://www.bilibili.com/video/BV1PX4y1g7KC?p=4