计算机视觉算法——DETR / Deformable DETR / DETR 3D

计算机视觉算法——DETR / Deformable DETR / DETR 3D

DETR是DEtection TRansformer的缩写，该方法发表于2020年ECCV，原论文名为《End-to-End Object Detection with Transformers》。

传统的目标检测是基于Proposal、Anchor或者None Anchor的方法，并且至少需要非极大值抑制来对网络输出的结果进行后处理，涉及到复杂的调参过程。而DETR使用了Transformer Encoder-Decoder的结构，并且通过集合预测损失实现了真正意义上的端到端的目标检测方法。Transformer Encoder-Decoder是怎么实现的？集合预测损失是什么？后文具体介绍。

对于目标检测方向不是很了解的同学可以参考计算机视觉算法——目标检测网络总结。

1. DETR

DETR网络结构如下图所示：

首先第一步是通过一个CNN对输入图片抽取特征，然后将特征图拉直输入Transformer Encoder-Decoder。第二步的Transformer Encoder部分就是使得网络更好地去学习全局的特征；第三步使用Transformer Decoder以及Object Query从特征中学习要检测的物体；第四步就是将Object Query的结果和真值进行二分图匹配（Set-to-Set Loss），最后在匹配上的结果上计算分类Loss和位置回归Loss。

以上是训练的基本过程，推理过程唯一的区别就是在第四步，第四步通过对Object Query设置一个阈值来输出最终检测的结果，这个结果不再需要进行进行任何后处理，而是直接作为最终的输出。

下面我们结合代码具体展开Transformer Encoder-Decoder和Set-to-Set Loss的细节：

1.1 Transformer Encoder-Decoder

Transformer Encoder-Decoder结构如下图所示，其中红色注释为输入为$3\times 800\times 1066$大小的图片后各个步骤Feature大小。

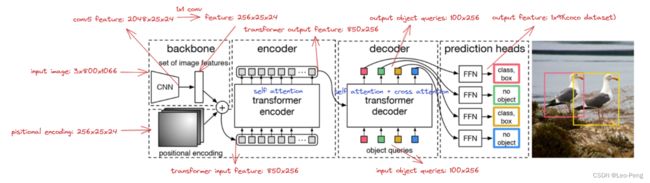
Transformer Encoder-Decoder的forward函数如下：

def forward(self, src, mask, query_embed, pos_embed):
        # flatten NxCxHxW to HWxNxC
        bs, c, h, w = src.shape
        src = src.flatten(2).permute(2, 0, 1)
        pos_embed = pos_embed.flatten(2).permute(2, 0, 1)
        query_embed = query_embed.unsqueeze(1).repeat(1, bs, 1)
        mask = mask.flatten(1)

        tgt = torch.zeros_like(query_embed)
        memory = self.encoder(src, src_key_padding_mask=mask, pos=pos_embed)
        hs = self.decoder(tgt, memory, memory_key_padding_mask=mask,
                          pos=pos_embed, query_pos=query_embed)
        return hs.transpose(1, 2), memory.permute(1, 2, 0).view(bs, c, h, w)

其中
src为Backbone抽取后的特征，输入Encoder前需要先对其进行展平处理；
pos_embed为位置编码，在DETR中位置编码是一个值固定的位置编码，具体参见下文有1.3中的介绍；
query_embed是一个可学习的位置编码，也就是上文体到的Object Query，其作用在Decoder中就是通过Encoder后的Feature和query_embed不断做Cross Attention，最query_embed的每一维就是一个检测结果的输出;
mask是DETR为了兼容不同分辨率图像作为输入，会在输入时将不同分别的图像Zero Padding成固定分辨率，Zero Padding部分不包含任何信息，因此不能用来计算Attention，因此作者在这里保留将Zero Padding部分传入了src_key_padding_mask。

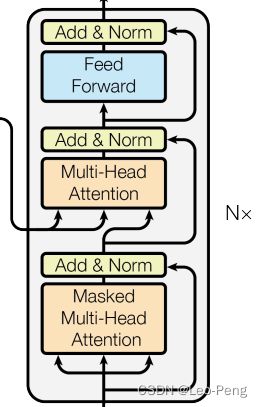
接下来的Encoder-Decoder部分和《Attention is All You Need》中几乎一致，Encoder层结构如下图所示：
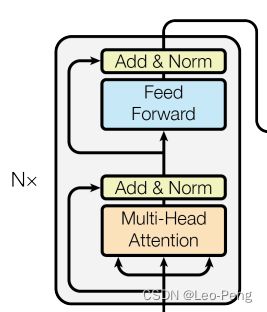代码如下：

def forward_post(self,
                 src,
                 src_mask: Optional[Tensor] = None,
                 src_key_padding_mask: Optional[Tensor] = None,
                 pos: Optional[Tensor] = None):
    q = k = self.with_pos_embed(src, pos)
    src2 = self.self_attn(q, k, value=src, attn_mask=src_mask,
                          key_padding_mask=src_key_padding_mask)[0]
    src = src + self.dropout1(src2)
    src = self.norm1(src)
    src2 = self.linear2(self.dropout(self.activation(self.linear1(src))))
    src = src + self.dropout2(src2)
    src = self.norm2(src)
    return src

Decoder结构如下图所示：
代码如下：

def forward_post(self, tgt, memory,
                 tgt_mask: Optional[Tensor] = None,
                 memory_mask: Optional[Tensor] = None,
                 tgt_key_padding_mask: Optional[Tensor] = None,
                 memory_key_padding_mask: Optional[Tensor] = None,
                 pos: Optional[Tensor] = None,
                 query_pos: Optional[Tensor] = None):
    q = k = self.with_pos_embed(tgt, query_pos)
    tgt2 = self.self_attn(q, k, value=tgt, attn_mask=tgt_mask,
                          key_padding_mask=tgt_key_padding_mask)[0]
    tgt = tgt + self.dropout1(tgt2)
    tgt = self.norm1(tgt)
    tgt2 = self.multihead_attn(query=self.with_pos_embed(tgt, query_pos),
                               key=self.with_pos_embed(memory, pos),
                               value=memory, attn_mask=memory_mask,
                               key_padding_mask=memory_key_padding_mask)[0]
    tgt = tgt + self.dropout2(tgt2)
    tgt = self.norm2(tgt)
    tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt))))
    tgt = tgt + self.dropout3(tgt2)
    tgt = self.norm3(tgt)
    return tgt

这里有个细节，除了第一层之外，query_embed在做Cross Attention之前，都需必须要做一次Self Attention，Self-Attention各个Query了解其他Query掌握的信息。

最后总结下，Transformer Encoder-Decoder有什么好处呢？
我觉得Transformer Encoder-Decoder应该是Set-to-Set成功的原因之一，在DETR之前其实也有一些文章提出Set-to-Set的想法，但是由于网络使用的Backbone不够强，因此并没有取得很好的效果。而Transformer Encoder-Decoder学习的是全局的特征，它可以使得其中某一个特征与全局里的其他特征都有了交互，网络就能更加清楚的知道哪里是一个物体，哪里是另外一个物体，一个物体应该就是对应一个输出，这也就更加符合Set-to-Set的假设。

1.2 Set-to-Set Loss

所谓Set-to-Set Loss就是将在计算网络损失前加一个二分图匹配的过程，使得最后预测结果只和匹配上的真值计算损失，如下公式所示：$$\hat{\sigma }=\underset{\sigma \in {\mathfrak{S}}_N}{\mathrm{argmin}}\sum _i^N{\mathcal{L}}_{\mathrm{match}}\left(y_i,{\hat{y}}_{\sigma (i)}\right)$$其中$y_i$为真值，${\hat{y}}_{\sigma (i)}$为预测值，${\mathcal{L}}_{\mathrm{match}}$为二分图匹配算法，对二分图匹配不熟悉的同学可以参考视觉SLAM总结——SuperPoint / SuperGlue中的介绍，区别是，在DETR代码码实现中调用的是scipy库中的linear_sum_assignment函数，该函数输入一个$M\times N$大小的Cost矩阵能计算$M$和$N$之间的匹配关系，在DETR中Cost矩阵由分类损失${\hat{p}}_{\sigma (i)}\left(c_i\right)$和Box损失${\mathcal{L}}_{\mathrm{box}}\left(b_i,{\hat{b}}_{\sigma (i)}\right)$两部分构成，分类损失为负的Softmax后的概率，Box损失为L1损失和Generalized IOU损失两部分构成如下：

def forward(self, outputs, targets):
        """ Performs the matching

        Params:
            outputs: This is a dict that contains at least these entries:
                 "pred_logits": Tensor of dim [batch_size, num_queries, num_classes] with the classification logits
                 "pred_boxes": Tensor of dim [batch_size, num_queries, 4] with the predicted box coordinates

            targets: This is a list of targets (len(targets) = batch_size), where each target is a dict containing:
                 "labels": Tensor of dim [num_target_boxes] (where num_target_boxes is the number of ground-truth
                           objects in the target) containing the class labels
                 "boxes": Tensor of dim [num_target_boxes, 4] containing the target box coordinates

        Returns:
            A list of size batch_size, containing tuples of (index_i, index_j) where:
                - index_i is the indices of the selected predictions (in order)
                - index_j is the indices of the corresponding selected targets (in order)
            For each batch element, it holds:
                len(index_i) = len(index_j) = min(num_queries, num_target_boxes)
        """
        bs, num_queries = outputs["pred_logits"].shape[:2]

        # We flatten to compute the cost matrices in a batch
        out_prob = outputs["pred_logits"].flatten(0, 1).softmax(-1)  # [batch_size * num_queries, num_classes]
        out_bbox = outputs["pred_boxes"].flatten(0, 1)  # [batch_size * num_queries, 4]

        # Also concat the target labels and boxes
        tgt_ids = torch.cat([v["labels"] for v in targets])
        tgt_bbox = torch.cat([v["boxes"] for v in targets])

        # Compute the classification cost. Contrary to the loss, we don't use the NLL,
        # but approximate it in 1 - proba[target class].
        # The 1 is a constant that doesn't change the matching, it can be ommitted.
        cost_class = -out_prob[:, tgt_ids]

        # Compute the L1 cost between boxes
        cost_bbox = torch.cdist(out_bbox, tgt_bbox, p=1)

        # Compute the giou cost betwen boxes
        cost_giou = -generalized_box_iou(box_cxcywh_to_xyxy(out_bbox), box_cxcywh_to_xyxy(tgt_bbox))

        # Final cost matrix
        C = self.cost_bbox * cost_bbox + self.cost_class * cost_class + self.cost_giou * cost_giou
        C = C.view(bs, num_queries, -1).cpu()

        sizes = [len(v["boxes"]) for v in targets]
        indices = [linear_sum_assignment(c[i]) for i, c in enumerate(C.split(sizes, -1))]
        return [(torch.as_tensor(i, dtype=torch.int64), torch.as_tensor(j, dtype=torch.int64)) for i, j in indices]

在求得匹配结果$\hat{\sigma }$后最终的损失大小为：$${\mathcal{L}}_{\text{Hungarian }}(y,\hat{y})=\sum _{i=1}^N\left[-\log {\hat{p}}_{\hat{\sigma }(i)}\left(c_i\right)+1_{\left\{c_i\ne \varnothing \right\}}{\mathcal{L}}_{\mathrm{box}}\left(b_i,{\hat{b}}_{\hat{\sigma }}(i)\right)\right]$$和匹配过程中使用的损失稍有不同的是这里的分类损失采用了通用的Cross Entropy损失，为什么有这样的区别论文中好像没有提到。在前文也提到过，二分匹配的过程仅仅出现在训练过程中，在测试过程中直接将网络输出的结果过一个阈值就得到最终的输出结果。

1.3 Positional Embedding

DETR中的Positional Embedding是一个固定值，Positional Embedding的代码如下，我们来简单剖析下：

class PositionEmbeddingSine(nn.Module):
    """
    This is a more standard version of the position embedding, very similar to the one
    used by the Attention is all you need paper, generalized to work on images.
    """
    def __init__(self, num_pos_feats=64, temperature=10000, normalize=False, scale=None):
        super().__init__()
        self.num_pos_feats = num_pos_feats
        self.temperature = temperature
        self.normalize = normalize
        if scale is not None and normalize is False:
            raise ValueError("normalize should be True if scale is passed")
        if scale is None:
            scale = 2 * math.pi
        self.scale = scale

    def forward(self, tensor_list: NestedTensor):
        x = tensor_list.tensors
        mask = tensor_list.mask
        assert mask is not None
        not_mask = ~mask
        y_embed = not_mask.cumsum(1, dtype=torch.float32)
        x_embed = not_mask.cumsum(2, dtype=torch.float32)
        if self.normalize:
            eps = 1e-6
            y_embed = y_embed / (y_embed[:, -1:, :] + eps) * self.scale
            x_embed = x_embed / (x_embed[:, :, -1:] + eps) * self.scale

        dim_t = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device)
        dim_t = self.temperature ** (2 * (dim_t // 2) / self.num_pos_feats)

        pos_x = x_embed[:, :, :, None] / dim_t
        pos_y = y_embed[:, :, :, None] / dim_t
        pos_x = torch.stack((pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4).flatten(3)
        pos_y = torch.stack((pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()), dim=4).flatten(3)
        pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2)
        return pos

为了使得网络感知到不同输入的位置信息，最直观的方式就是给第一个Feature赋值$1$，第二个Feature赋值$2$，但是这种赋值方式对于较大的输入是不友好的，因此有人提出使用正弦函数将值控制在$-1$和$1$之间，但是正弦函数又具备周期性，可能会造成不同位置值相同的情况。

因此作者将正弦函数扩展到$d$维向量，不同通道具备不同的波长，如下：
$$P{E}_{(pos,2i)}=\sin \left(pos/10000^{2i/d_{\text{model }}}\right)$$$$P{E}_{(\text{pos },2i+1)}=\cos \left(pos/10000^{2i/d_{\text{model }}}\right)$$其中$i$为通道数，举例来说，我们令$d=6$那么：$$i=[1,2,3,4,5,6]$$$$w_i=\left[\frac{1}{10000^{1/6}},\frac{1}{10000^{2/6}},\frac{1}{10000^{3/6}},\frac{1}{10000^{4/6}},\frac{1}{10000^{5/6}},\frac{1}{10000^{6/6}}\right]$$当$Poision=2$时，得到：$$PositionEncoding=\left[\sin \left(2w_0\right),\cos \left(2w_1\right),\sin \left(2w_2\right),\cos \left(2w_3\right),\sin \left(2w_4\right),\cos \left(2w_5\right)\right]$$这样得到的一个多维向量在不同位置上很难会相同，因此也就达到对不同位置进行编码的效果。

DETR提出后以其简单的结构很快得到了大家的关注，DETR本身也存在很多问题，例如训练收敛速度不够快，结果不够SOTA，对小物体检出效果较差等，因此紧接着就出现了很多DETR相关的算法，例如Deformable DETR、Anchor DETR等，以及应用到自动驾驶领域的DETR3D等等，这里我对其中部分算法简单总结下。

2. Deformable DETR

Deformable DETR主要解决原始DETR训练速度慢以及对小物体检测效果差的问题。DETR收敛速度慢主要是由于Attention Map从均匀分布到稀疏分布的训练过程非常耗时，对于小物体检测效果差主要是因为Backbone没有多尺度特征，但即使有，将多尺度特征输入Transformer也不现实，因为Transfomer的计算复杂度是$O(n^2)$，高分辨率的特征会带来巨大的内存和时间消耗。

为此，Deformable DETR提出了Defomer Attention模块使得以上问题得到了很好的解决。

2.1 Deformable Attention Module

作者首先在论文中介绍了原始Transformer中多头注意力机制的公式：$$\text{ MultiHeadAttn }\left(z_q,x\right)=\sum _{m=1}^M{W}_m\left[\sum _{k\in {\Omega }_k}{A}_{mqk}\cdot W_m^{\prime }{x}_k\right]$$这和我们平常看到的公式原理是相同的，只是表达略微有些不同。其中$z_q,x$分别为进行Attention的两组向量，$V_{m}x$得到Key Embedding，$U_m{z}_q$得到Query Embedding，$A_{mqk}$为Query Embedding和Key Embedding点乘后的归一化得到权重，正比于$\exp \left\{\frac{z_q^T{U}_m^T{V}_m{x}_k}{\sqrt{C_v}}\right\}$。$W_m^{\prime }{x}_k$为Value Embedding，$W_m$则负责将Concate后的多头结果进行聚合。其中$U_m,V_m,W_m^{\prime },W_m$均为学习的参数。在DETR中就是将这样原始的多头注意力机制应用到Encoder的Self-Attention和Decoder的Cross-Attention中。

接下来作者介绍了Deformable Attention Module的原理，表达公式为：$$\mathrm{DeformAttn}\left({\mathbf{z}}_q,{\mathbf{p}}_q,\mathbf{x}\right)=\sum _{m=1}^M{\mathbf{W}}_m\left[\sum _{k=1}^K{A}_{mqk}\cdot {\mathbf{W}}_m^{\prime }\mathbf{x}\left({\mathbf{p}}_q+\Delta {\mathbf{p}}_{mqk}\right)\right]$$其中$\delta p_{mqk}$是从Query Embedding获得的位置偏移，而公式中的$A_{mqk}$也不再是通过Query Embedding和Key Embedding点乘获得的权重，而是直接从Query Embedding获得的权重，这一过程可以通过下图去理解：

与DETR中使用的多头注意力机制不同的点在于：

1. DETR中使用的多头注意力机制是使用全局特征作为Key值，而Deformable Attention是在每个Query附近，通过Query Embedding自主选取$K$个Key值；
2. DETR中使用的多头注意力机制是通过Key Embedding和Query Embedding做内积获得权重，而Deformable Attention则是直接由Query Embedding经过一个线性层获得。

也正是以上两处不同点，使得Deformable Attention相对原始的Attention机制要更加高效。另外补充下，Deformable Attention和Deformable Convolution也是有不同的，Deformable Attention是在Query位置的一个点上直接预测多个偏移量，而Deformable Convolution则是对卷积核内的每个像素都预测一个偏移量。

在Deformable Attention Module的基础上，作者又进一步提出了Multi Scale Deformable Attention Module，公式如下：$$\mathrm{MSDeformAttn}\left(z_q,{\hat{\mathbf{p}}}_q,{\left\{x^l\right\}}_{l=1}^L\right)=\sum _{m=1}^M{W}_m\left[\sum _{l=1}^L\sum _{k=1}^K{A}_{mlqk}\cdot {\mathbf{W}}_m^{\prime }{\mathbf{x}}^l\left({\varphi }_l\left({\hat{\mathbf{p}}}_q\right)+\Delta {\mathbf{p}}_{mlqk}\right)\right]$$和Deformable Attention Module相比，区别主要在于Deformable Attention Module是从当前层采样$K$个位置，而Multi Scale Deformable Attention Module则是从$L$层每层采样$K$个位置，共$LK$个采样位置。这样就使得网络以一个较小的代价实现了多尺度特征的融合。

2.2 Deformable Transformer Encoder-Decoder

Deformable Transformer Encoder-Decoder结构如下图所示：

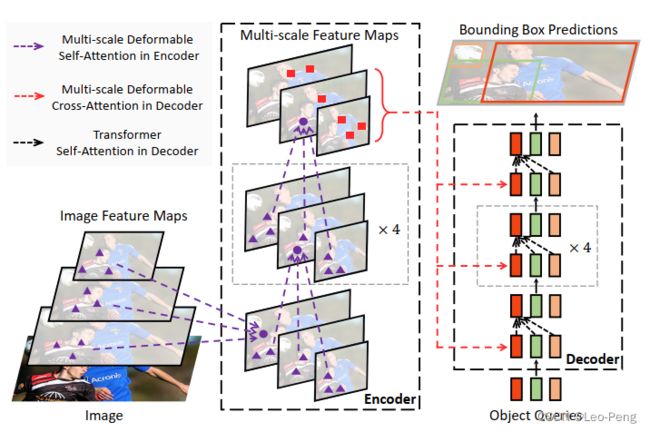
在Encoder中，作者将Self-Attention Module全部更换为Deformable Attention Module，每个Encoder的输入输出都是相同分辨率的多尺度特征图。多尺度特征图直接来自于ResNet的最后三个Stage。如下图所示：

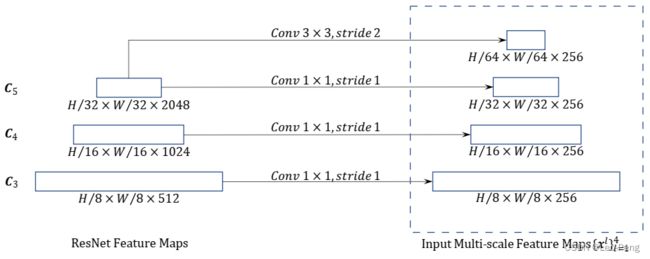
除此之外，在保留Positional Embedding的基础上，还添加了一个和特征层数相关可学习的Scale-Level Embedding。

在Decoder中，作者保持了Self-Attention不变，而将Cross-Attention更换为了Deformable Attention，对于每一个Object Query Embedding，由线性层和Sigmoid学习出其对应的参考点并在Encoder输出的Feature上Query出对应的Value Embedding，最后基于由线性层和Softmax学习出的权重进行加权求和。第一次读到这里时，我有这么一个疑问：Object Query Embeding是一个预设的值，如果参考点位置和权重都是从Object Query Embedding推理的来的（DETR中都是通过和Encoder Feature关联得到的），那怎么能够保证检测的目标就是对的呢？ 后来仔细一想，第一层Decode Layer的参考点或者权重确实可能是一个固定值或随机值，但是在第一层Decode Layer输出的Object Query Embdding中就已经包含了Encoder Feature的信息，在第二层Decoder Layer生成的参考点位置就会和图像开始相关，而随着Decoder Layer的叠加，这个相关性还会越来越强。

此外，和DETR还有一点不同的是，Deformable DETR预测Bounding Box并不是从Object Query直接回归出绝对的坐标，而是回归出对参考点的距离，由于权重和参考点位置都是从同一个Object Query Embedding推理出来的，因此回归相对于参考点这样的作法能够加快收敛。

2.3 Conclusion

关于Deformable DETR的知识点远不止本文上面总结的两点，在Deformable DETR的论文还介绍了Two-Stage Defomable DETR等其他网络结构，还可以深入挖掘，这里我们来对比下Deformable DETR相对DETR的提升：
以下是训练速度的对比，Deformable DETR的训练收敛速度明显提升了不少：

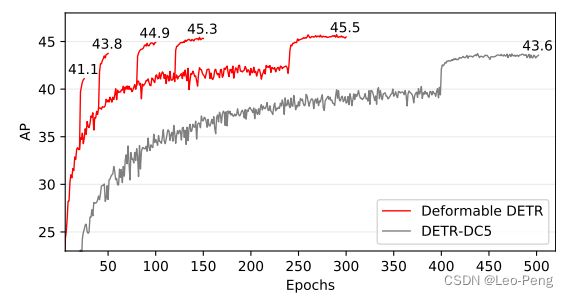
从下面的表格中我们可以看到在小物体的检测精度上，Deformable提升了很多：

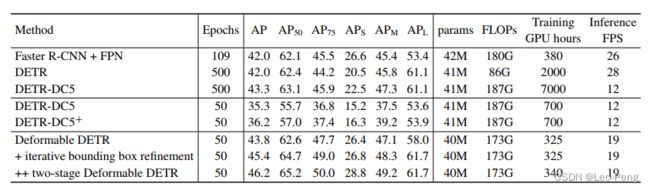
DETR的提出主要是以其端到端的网络结构出圈，但是其性能可能在当时还没有达到SOTA，而在Deformable DETR的加持下，这类方法已经可以和SOTA方法一战了，对比结果如下：

3. DETR3D

DETR3D是将DETR应用到自动驾驶领域，实现多相机输入BEV视角下的3D物体检测，如下图所示：
其原理和上文提到的Deformable Transformer很像，下面简单先总结下，关于Transformer在BEV视角任务下的应用像后面另起一篇博客学习下。

网络的结构图下图所示：

网络先通过ResNet和FPN对各路摄像头输入都提取多尺度的特征，也即是图中的Image Feature Extraction部分，这没啥好说的，接下来就是将多尺度的特征输入2D to 3D Feature Transformation进行进一步学习，下面详细介绍下这部分内容。

3.1 2D to 3D Transfomer

每路相机输入我们提取四个尺度的特征，分别记为${\mathcal{F}}_1,{\mathcal{F}}_2,{\mathcal{F}}_3,{\mathcal{F}}_4$，在论文的配置下是一共有六路相机输入：${\mathcal{F}}_k=\left\{{\mathbf{f}}_{k1},\dots ,{\mathbf{f}}_{k6}\right\}\subset {\mathbb{R}}^{H\times W\times C}$。

在DETR3D算法中是没有基于Transfomer的Encoder部分的，而是上述提取的图像特征是直接输入了Decoder部分。原因我觉得应该就是Encoder部分计算量太大了，而在Decoder部分和DETR或者Deformable DETR一样，都是通过Object Query Embedding和输入的Feature进行Cross Attention，进而从最后输出的Object Query Embedding中回归出对应的类别和位置，在DETR3D中区别较大的是回归的3D空间下的位置，而输入的是2D图像的Feature，因此也就需要这样一个2D to 3D Transfomer的Decoder.

DETR3D的Decoder仍然是由Self-Attention和Cross-Attention构成，Self-Attention和DETR中的方法基本一致，主要作用就是保证各个Query之间知道对方在干嘛，避免重复提取相同的特征，而Cross-Attention则区别较大，下面我们来看下具体步骤：

1. 首先通过一个独立的网络${\Phi }^{\text{ref }}$从Object Query Embedding中回归出一个3D位置，这和Deformable DETR的操作有些类似：$${\mathbf{c}}_{\ell i}={\Phi }^{\mathrm{ref}}\left({\mathbf{q}}_{\ell i}\right)$$其中${\mathbf{c}}_{\ell i}$可以被认为是第$i$个Box的中心位置。
2. 通过相机参数，将位置${\mathbf{c}}_{\ell i}$投影到各个相机的Feature上去获得用于Key Embedding和Value Embedding来Refine预测的Box的3D位置：$${\mathbf{c}}_{\ell i}^{\ast }={\mathbf{c}}_{\ell i}\oplus 1$$$${\mathbf{c}}_{\ell mi}=T_m{\mathbf{c}}_{\ell i}^{\ast }$$其中$T_m$为相机参数。
3. 由于每一路输入都是多尺度的特征图，为了避免不同尺度特征分辨率的影响，采用双线性插值来对特征图进行插值，如果坐标落到图片外则补零：$${\mathbf{f}}_{\ell kmi}=f^{\text{bilinear }}\left({\mathcal{F}}_{km},{\mathbf{c}}_{\ell mi}\right)$$
4. 将以上特征相加，并最后加入Object Query Embedding中来进行Refinement：$${\mathbf{f}}_{\ell i}=\frac{1}{{\sum }_k{\sum }_m{\sigma }_{\ell kmi}+ϵ}\sum _k\sum _m{\mathbf{f}}_{\ell kmi}{\sigma }_{\ell kmi}$$$${\mathbf{q}}_{(\ell +1)i}={\mathbf{f}}_{\ell i}+{\mathbf{q}}_{\ell i}$$我认为这里其实就是相当于Cross Attention加权求和的步骤，在DETR中这一步是通过Query Embedding和Key Embedding点乘后的权重，加权Value Embedding的值来更新Query。在Deformable中则将Query Embedding和Key Embedding点乘的步骤省略，直接通过Query Embedding进行回归权重，然后加权Value Embedding。而在这里，作者相当于将Value Embedding和Query Embedding相加，进一步省略了计算量。（这一部分是我根据论文的描述和其他博客的总结得到的结论，可能和代码实现还有不同，有误的话还请读者指出）
5. 在对以上操作迭代多次后，最终从Query Embeding中回归出类别和位置：$${\hat{\mathbf{b}}}_{\ell i}={\Phi }_{\ell }^{\mathrm{reg}}\left({\mathbf{q}}_{\ell i}\right)$$$${\hat{c}}_{\ell i}={\Phi }_{\ell }^{\mathrm{cls}}\left({\mathbf{q}}_{\ell i}\right)$$

以上就是DETR3D Decoder部分的理解，由于暂时还没有时间去阅读源码，理解可能还不是很充分，很多细节可能也忽略了。从去年Tesla AI Day之后，大家对于Transfomer在自动驾驶领域的应用就展开了非常多的研究，我之后也打算再更进下，怎样将2D Feature在3D中关联起来感觉挺有意思的一个事情。

本篇关于DETR的相关总结暂时到这，后面有时间再补充，如有问题欢迎指教，欢迎交流~