径向基RBF(radial basis function)函数、RBF神经网络、 反推(back-stepping)控制
| 径向基 | |
|---|---|
| 1 | 径向基RBF(radial basis function)函数、RBF神经网络、 反推(back-stepping)控制 |
文章目录
- 1. 什么是径向基函数
-
- 1.1 高斯径向基函数
- 1.2 反演S型函数
- 1.3 拟多二次函数
- 2. 正则化径向基神经网络
1. 什么是径向基函数
理解RBF网络的工作原理可从两种不同的观点出发:
- 当用RBF网络解决非线性映射问题时,用函数逼近与内插的观点来解释,对于其中存在的不适定(illposed)问题,可用正则化理论来解决;
- 当用RBF网络解决复杂的模式分类任务时,用模式可分性观点来理解比较方便,其潜在合理性基于Cover关于模式可分的定理。
下面阐述基于函数逼近与内插观点的工作原理。
1963年Davis提出高维空间的多变量插值理论。径向基函数技术则是20世纪80年代后期,Powell在解决“多变量有限点严格(精确)插值问题”时引人的,目前径向基函数已成为数值分析研究中的一个重要领域。
考虑一个由 N N N 维输人空间到一维输出空间的映射。设 N N N 维空间有 p p p 个输入向量, p = 1 , 2 , ⋯ , P p=1,2,\cdots,P p=1,2,⋯,P,它们在输出空间相应的目标值为 d p , p = 1 , 2 , . . . , P d^p,~p=1,2,...,P dp, p=1,2,...,P, P P P 对输人一输出样本构成了训练样本集。插值的目的是寻找一个非线性映射函数 F ( X ) F(X) F(X),使其满足下述插值条件:
F ( X ) = d p , p = 1 , 2 , ⋯ , P (1) F(X) = d^p,~~~~p=1,2,\cdots,P \tag{1} F(X)=dp, p=1,2,⋯,P(1)
式子中,函数 F F F 描述了一个插值曲面,所谓严格插值或精确插值,是一种完全内插,即该插值曲面必须通过所有训练数据点。
那么到底什么是插值,在这里简单的解释一下,就是通过训练集数据,我找到一个曲面,这个曲面可以完全覆盖这些训练点,那么找到这个曲面后就可以通过这个曲面取寻找其他的值了,下面画个图给大家看看:
就是我通过一些数据样本点 ,每个样本都有目标值,通映射高维空间去找到一个曲面 F ( x ) F(x) F(x),这个曲面需要经过所有的数据,一旦这个曲面确定以后,我就可以通过这个曲面去生成更多的数据目标值,就是这个意思了,好,我们继续往下:
采用径向基函数技术解决插值问题的方法是,选择 P P P 个基函数个训练数据,各基函数的形式为:
φ ( ∥ x − x p ∥ ) , p = 1 , 2 , ⋯ , P (2) \varphi(\|x-x^p\|),~~~p=1,2,\cdots,P \tag{2} φ(∥x−xp∥), p=1,2,⋯,P(2)
式中,基函数 φ \varphi φ 为非线性函数,训练数据点 x P x^P xP 是 φ \varphi φ 的中心。
基函数以输入空间的点 x x x 与中心 x P x^P xP 的距离作为函数的自变量。由于距离是径向同性的,故函数被称为径向基函数。
基于径向基函数技术的插值函数定义为基函数的线性组合:
F ( x ) = ∑ p = 1 P w p φ ( ∥ x − x P ∥ ) (3) F(x) = \sum_{p=1}^{P} w_p \varphi(\|x-x^P\|) \tag{3} F(x)=p=1∑Pwpφ(∥x−xP∥)(3)
在这里解释一下 ∥ x − x P ∥ \|x-x^P\| ∥x−xP∥,这是范数。对平面几何的向量来说就是模,然而一旦维度很高就不知道是什么东西了,可能是衡量距离的一个东西,那么这个代表什么意思呢?简单来说就是一个圆而已,在二维平面, x P x^P xP 就是圆心, x x x 就是数据了,这个数据距离圆心的距离,因为和数据的位置和大小无关,只和到圆心的半径有关,况且同一半径圆上的点到圆心是相等的因此取名为径向,代入映射函数就是径向基函数了,我们看看径向基函数有什么特点:
将 (1) 式的插值条件代入上式,得到 P P P 个关于未知系数 w p , p = 1 , 2 , ⋯ , P w^p, p=1,2,\cdots,P wp,p=1,2,⋯,P 的线性方程组:
∑ p = 1 P w p φ ( ∥ x 1 − x p ∥ ) = d 1 ∑ p = 1 P w p φ ( ∥ x 2 − x p ∥ ) = d 2 ⋮ ∑ p = 1 P w p φ ( ∥ x P − x p ∥ ) = d P \begin{aligned} \sum_{p=1}^{P} w_p \varphi(\|x^1 - x^p\|) &= d^1 \\ \sum_{ p=1}^{P} w_p \varphi(\|x^2 - x^p\|) &= d^2 \\ &\vdots \\ \sum_{p=1}^{P} w_p \varphi(\|x^P - x^p\|) &= d^P \\ \end{aligned} p=1∑Pwpφ(∥x1−xp∥)p=1∑Pwpφ(∥x2−xp∥)p=1∑Pwpφ(∥xP−xp∥)=d1=d2⋮=dP
令 φ i p = φ ( ∥ x i − x p ∥ ) \varphi_{ip}=\varphi(\|x^i - x^p\|) φip=φ(∥xi−xp∥), i = 1 , 2 , ⋯ , P i=1,2,\cdots,P i=1,2,⋯,P, p = 1 , 2 , ⋯ , P p=1,2,\cdots,P p=1,2,⋯,P,则上述方程组可改写为:
[ φ 11 φ 12 ⋯ φ 1 P φ 11 φ 12 ⋯ φ 1 P ⋮ ⋮ ⋱ ⋮ φ 11 φ 12 ⋯ φ 1 P ] [ w 1 w 2 ⋮ w P ] = [ d 1 d 2 ⋮ d P ] (5) \left[\begin{matrix} \varphi_{11} & \varphi_{12} & \cdots & \varphi_{1P} \\ \varphi_{11} & \varphi_{12} & \cdots & \varphi_{1P} \\ \vdots & \vdots & \ddots & \vdots \\ \varphi_{11} & \varphi_{12} & \cdots & \varphi_{1P} \\ \end{matrix}\right] \left[\begin{matrix} w_1 \\ w_2 \\ \vdots \\ w_P \\ \end{matrix}\right]= \left[\begin{matrix} d_1 \\ d_2 \\ \vdots \\ d_P \\ \end{matrix}\right]\tag{5} ⎣ ⎡φ11φ11⋮φ11φ12φ12⋮φ12⋯⋯⋱⋯φ1Pφ1P⋮φ1P⎦ ⎤⎣ ⎡w1w2⋮wP⎦ ⎤=⎣ ⎡d1d2⋮dP⎦ ⎤(5)
令 Φ \Phi Φ 表示元素 φ i p \varphi_{ip} φip 的 P × P P\times P P×P 阶矩阵, W W W 和 d d d 分别表示系数向量和期望输出向量,(5) 式还可以写成下面的向量形式:
Φ W = d (6) \Phi W = d \tag{6} ΦW=d(6)
式中, Φ \Phi Φ 称为插值矩阵,若 Φ \Phi Φ 为可逆矩阵,就可以从 (6) 式中解出系数向量 W W W,即:
W = Φ − 1 d (7) W = \Phi^{-1}d \tag{7} W=Φ−1d(7)
通过上面大家可以看到为了使所有数据都在曲面还需要系数调节,此时求出系数向量就求出了整个的映射函数了,下面看几个特殊的映射函数:
1.1 高斯径向基函数
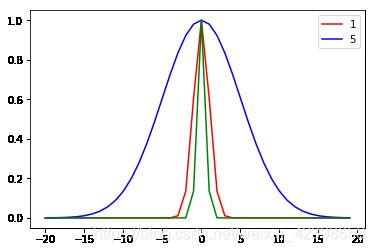
φ ( r ) = exp ( − r 2 2 δ 2 ) \varphi(r) = \exp(-\frac{r^2}{2\delta^2}) φ(r)=exp(−2δ2r2)
横轴就是到中心的距离,用半径 r r r 表示。如上图,我们发现当距离等于 0 时,径向基函数等于 1,距离越远衰减越快,其中高斯径向基的参数 δ \delta δ 在支持向量机中被称为到达率或者说函数跌落到零的速度。
红色 δ = 1 \delta=1 δ=1,蓝色 δ = 5 \delta=5 δ=5,绿色 δ = 0.5 \delta=0.5 δ=0.5,我们发现到达率越小其越窄。
1.2 反演S型函数
1.3 拟多二次函数
2. 正则化径向基神经网络
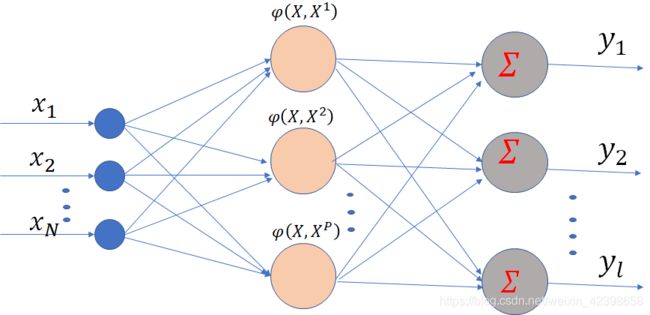
正则化RBF网络的结构如下图所示。其特点是:网络具有 N N N 个输人节点, P P P 个隐节点, i i i 个输出节点;网络的隐节点数等于输人样本数,隐节点的激活函数常高斯径向基函数,并将所有输人样本设为径向基函数的中心,各径向基函数取统一的扩展常数。
设输入层的任意节点你用 i i i 表示,隐节点任意节点用 j j j 表示,输出层的任一节点用 k k k 表示。对各层的数学描述如下:
输入向量:
X = ( x 1 , x 2 , ⋯ , x N ) T X = (x_1, x_2, \cdots, x_N)^T X=(x1,x2,⋯,xN)T
任一隐节点的激活函数:
φ j ( X ) , ( j = 1 , 2 , ⋯ , P ) \varphi_j(X),~~~~(j=1,2,\cdots,P) φj(X), (j=1,2,⋯,P)
称为基函数,一般使用高斯函数。
输出权矩阵:
W W W
其中, w i k , ( j = 1 , 2 , ⋯ , P , k = 1 , 2 , ⋯ , l ) w_{ik},(j=1,2,\cdots,P, k=1,2,\cdots,l) wik,(j=1,2,⋯,P,k=1,2,⋯,l) 为隐层的第 j j j 个节点与输出层第 k k k 个节点间的突触权值。
输出向量:
Y = ( y 1 , y 2 , ⋯ , y l ) Y = (y_1, y_2, \cdots, y_l) Y=(y1,y2,⋯,yl)
输出层神经元采用线性激活函数。
当输入训练集中的某个样本 x p x^p xp 时,对应的期望输出 d p d^p dp 就是教师信号。为了确定网络隐层到输出层之间的 P P P 个权值,需要将训练集中的样本逐一输入一遍,从而得到式 (4) 中的方程组。网络的权值确定后,对训练集的样本实现了完全内插,即对所有样本误差为 0。而对非训练集的输入模式,网络的输出值相当于函数的内插,因此径向基函数网络可用作数逼近。
正则化RBF网络具有以下3个特点:
- 正则化网络是一种通用逼近器,只要有足够的节点,它可以以任意精度逼近紧集上的任意多元连续函数;
- 具有最佳逼近特性,即任给一个未知的非线性函数 f f f,总可以找到一组权值使得正则化网络对于 f f f 的逼近优于所有其可能的选择;
- 正则化网络得到的解是最佳的,所谓“最佳”体现在同时满足对样本的逼近误差和逼近曲线的平滑性。
Ref: 机器学习–支持向量机(六)径向基核函数(RBF)详解
Ref: 深度学习 — 径向基神经网络RBF详解