深度学习推荐系统算法简单了解01：协同过滤算法

0、知识快速介绍

简单说就是找相似，那么第一时间想到的数学方法就是线性相关性、余弦公式。
实现协同过滤,需要以下几个步骤：

1)收集用户偏好。 （搜寻数据）
2)找到相似的用户或物品。（制作数据集和特征提取）
3)计算并推荐。（算法方法、策略）

在一个推荐系统中,用户行为都会多于一种。那么,如何
组合这些不同的用户行为呢?基本上有如下两种方式。

将不同的行为分组
对不同行为进行加权(减噪, 归一化等)

在推荐的场景中,在用户-物品偏好的二维矩阵中,我们可以将一个用户
对所有物品的偏好作为一个向量来计算用户之间的相似度,或者将所有用户对某个物品的偏好作为一个向量来计算物品之间的相似度。下面详细介绍几种常用的相似度计算方法：

同现相似度：物品A和物品B的同现相似度公式定义如下:

欧几里得距离(Euclidean Distance)

皮尔逊相关系数(Pearson Correlation Coefficient)

Cosine相似度(Cosine Similarity)

Tanimoto系数(Tanimoto Coefficient)

案例分析：
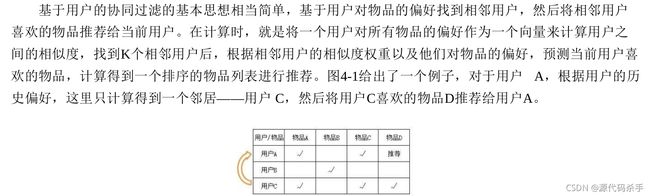
基于用户的协同过滤(UserCF)

基于物品的协同过滤(ItemCF)
基于物品的协同过滤的原理和基于用户的协同过滤的原理类似,只是在计算邻居时采用物品本身(而不是从用户的角度),即基于用户对物品的偏好找到相似的物品,然后根据用户的历史偏好推荐相似的物品给他。从计算的角度看,就是将所有用户对某个物品的偏好作为一个向量来计算物品之间的相似度,得到某物品的相似物品后,如根据用户的历史偏好预测当前用户还没有表示偏好的物品,则计算得到一个排序的物品列表进行推荐。图4-2给出了一个例子,对于物品A,根据所有用户的历史偏好喜欢物品A的用户都喜欢物品C,得出物品A和物品C比较相似,而用户C喜欢物品A,那么可以推断出用
户C可能也喜欢物品C。

1、算法源码实现

源码主要实现内容：

fit(self, data):计算所有用户的推荐物品
CF_knearest(CF_base):基于物品的K近邻协同过滤推荐算法
cal_similarity(self, i, j, data):计算物品i和物品j的相似度
cal_simi_mat(self, data):计算物品间的相似度矩阵
cal_prediction(self, user_row, item_ind):计算预推荐物品i对目标活跃用户u的吸引力
cal_recommendation(self, user_ind, data):计算目标用户的最具吸引力的k个物品list
CF_svd(CF_base):基于矩阵分解的协同过滤算法
svd_simplify(self, data):奇异值分解以及简化
cal_prediction(self, user_ind, item_ind, user_row):两个隐因子向量的内积加上平均值就是最终的预测分值
cal_recommendation(self, user_ind, data):计算目标用户的最具吸引力的k个物品list

"""
协同过滤算法
"""
from abc import ABCMeta, abstractmethod
import numpy as np
from collections import defaultdict


class CF_base(metaclass=ABCMeta):
    def __init__(self, k=3):
        self.k = k
        self.n_user = None
        self.n_item = None

    @abstractmethod
    def init_param(self, data):
        pass

    @abstractmethod
    def cal_prediction(self, *args):
        pass

    @abstractmethod
    def cal_recommendation(self, user_id, data):
        pass

    def fit(self, data):
        # 计算所有用户的推荐物品
        self.init_param(data)
        all_users = []
        for i in range(self.n_user):
            all_users.append(self.cal_recommendation(i, data))
        return all_users


class CF_knearest(CF_base):
    """
    基于物品的K近邻协同过滤推荐算法
    """

    def __init__(self, k, criterion='cosine'):
        super(CF_knearest, self).__init__(k)
        self.criterion = criterion
        self.simi_mat = None
        return

    def init_param(self, data):
        # 初始化参数
        self.n_user = data.shape[0]
        self.n_item = data.shape[1]
        self.simi_mat = self.cal_simi_mat(data)
        return

    def cal_similarity(self, i, j, data):
        # 计算物品i和物品j的相似度
        items = data[:, [i, j]]
        del_inds = np.where(items == 0)[0]
        items = np.delete(items, del_inds, axis=0)
        if items.size == 0:
            similarity = 0
        else:
            v1 = items[:, 0]
            v2 = items[:, 1]
            if self.criterion == 'cosine':
                if np.std(v1) > 1e-3:  # 方差过大，表明用户间评价尺度差别大需要进行调整
                    v1 = v1 - v1.mean()
                if np.std(v2) > 1e-3:
                    v2 = v2 - v2.mean()
                similarity = (v1 @ v2) / np.linalg.norm(v1, 2) / np.linalg.norm(v2, 2)
            elif self.criterion == 'pearson':
                similarity = np.corrcoef(v1, v2)[0, 1]
            else:
                raise ValueError('the method is not supported now')
        return similarity

    def cal_simi_mat(self, data):
        # 计算物品间的相似度矩阵
        simi_mat = np.ones((self.n_item, self.n_item))
        for i in range(self.n_item):
            for j in range(i + 1, self.n_item):
                simi_mat[i, j] = self.cal_similarity(i, j, data)
                simi_mat[j, i] = simi_mat[i, j]
        return simi_mat

    def cal_prediction(self, user_row, item_ind):
        # 计算预推荐物品i对目标活跃用户u的吸引力
        purchase_item_inds = np.where(user_row > 0)[0]
        rates = user_row[purchase_item_inds]
        simi = self.simi_mat[item_ind][purchase_item_inds]
        return np.sum(rates * simi) / np.linalg.norm(simi, 1)

    def cal_recommendation(self, user_ind, data):
        # 计算目标用户的最具吸引力的k个物品list
        item_prediction = defaultdict(float)
        user_row = data[user_ind]
        un_purchase_item_inds = np.where(user_row == 0)[0]
        for item_ind in un_purchase_item_inds:
            item_prediction[item_ind] = self.cal_prediction(user_row, item_ind)
        res = sorted(item_prediction, key=item_prediction.get, reverse=True)
        return res[:self.k]


class CF_svd(CF_base):
    """
    基于矩阵分解的协同过滤算法
    """

    def __init__(self, k=3, r=3):
        super(CF_svd, self).__init__(k)
        self.r = r  # 选取前k个奇异值
        self.uk = None  # 用户的隐因子向量
        self.vk = None  # 物品的隐因子向量
        return

    def init_param(self, data):
        # 初始化，预处理
        self.n_user = data.shape[0]
        self.n_item = data.shape[1]
        self.svd_simplify(data)
        return data

    def svd_simplify(self, data):
        # 奇异值分解以及简化
        u, s, v = np.linalg.svd(data)
        u, s, v = u[:, :self.r], s[:self.r], v[:self.r, :]  # 简化
        sk = np.diag(np.sqrt(s))  # r*r
        self.uk = u @ sk  # m*r
        self.vk = sk @ v  # r*n
        return

    def cal_prediction(self, user_ind, item_ind, user_row):
        rate_ave = np.mean(user_row)  # 用户已购物品的评价的平均值(未评价的评分为0)
        return rate_ave + self.uk[user_ind] @ self.vk[:, item_ind]  # 两个隐因子向量的内积加上平均值就是最终的预测分值

    def cal_recommendation(self, user_ind, data):
        # 计算目标用户的最具吸引力的k个物品list
        item_prediction = defaultdict(float)
        user_row = data[user_ind]
        un_purchase_item_inds = np.where(user_row == 0)[0]
        for item_ind in un_purchase_item_inds:
            item_prediction[item_ind] = self.cal_prediction(user_ind, item_ind, user_row)
        res = sorted(item_prediction, key=item_prediction.get, reverse=True)
        return res[:self.k]


if __name__ == '__main__':
    data = np.array([[4, 3, 0, 5, 0],
                     [4, 0, 4, 4, 0],
                     [4, 0, 5, 0, 3],
                     [2, 3, 0, 1, 0],
                     [0, 4, 2, 0, 5]])
    # data = np.array([[3.5, 1.0, 0.0, 0.0, 0.0, 0.0],
    #                  [2.5, 3.5, 3.0, 3.5, 2.5, 3.0],
    #                  [3.0, 3.5, 1.5, 5.0, 3.0, 3.5],
    #                  [2.5, 3.5, 0.0, 3.5, 4.0, 0.0],
    #                  [3.5, 2.0, 4.5, 0.0, 3.5, 2.0],
    #                  [3.0, 4.0, 2.0, 3.0, 3.0, 2.0],
    #                  [4.5, 1.5, 3.0, 5.0, 3.5, 0.0]])
    cf = CF_svd(k=1, r=3)
    # cf = CF_knearest(k=1)
    print(cf.fit(data))