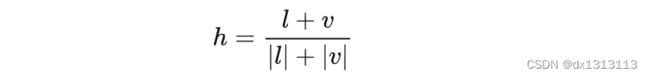Blinn-Phong光照模型详解
Blinn-Phong光照模型,又称为Blinn-phong反射模型(Blinn–Phong reflection model)或者 phong 修正模型(modified Phong reflection model),是由 Jim Blinn于 1977 年在文章中对传统 phong 光照模型基础上进行修改提出的。它是一个经验模型,并不完全符合真实世界中的光照现象,但由于实现起来简单方便,并且计算速度和得到的效果都还不错,因此在早期被广泛的使用。
它将进入摄像机的光线分为三个部分,每个部分使用一种方法来计算它的贡献度,这三个部分分别是环境光(Ambient)、漫反射(Diffuse)和高光反射(Specular)。
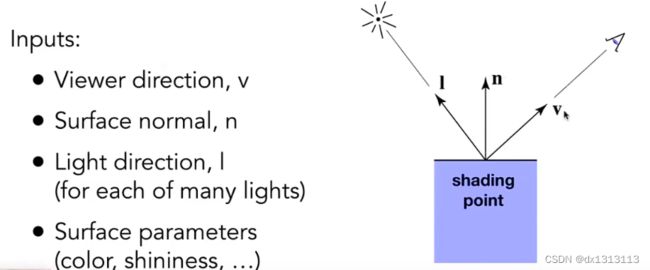
在计算之前,我们先定义一些基本的向量,因为只表示方向,默认它们都为单位向量。
Viewer direction,观察方向,使用v表示Surface normal,法线方向,使用n表示Light direction,光线方向,使用l(小写的L)表示- Surface parameters ,一些其他参数
下面首先先介绍一下环境光、漫反射和高光反射的定义
-
环境光
环境光也称间接光,为了防止画面在没有光照条件下为一片漆黑的状态而引入的一种定义,可以当做物体自发光。是一个常量。
-
漫反射
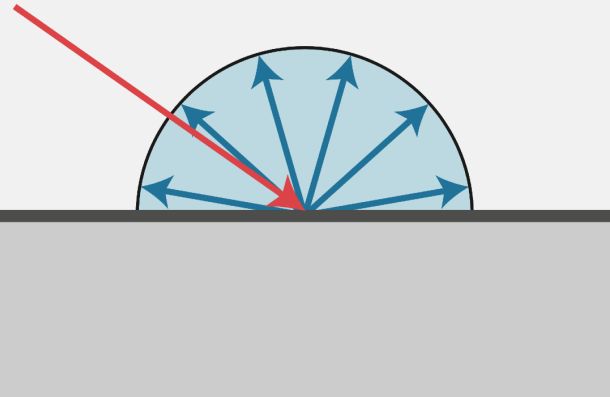
当光线照射到一个点时,该光线会被均匀的反射到各个方向,这种反射称为漫反射。也就是说,在漫反射中,视角的位置是不重要的,因为反射是完全随机的,因此可以认为漫反射光在任何反射方向上的分布都是一样的,如下图所示
那影响漫反射光照强度的因素有哪些呢?
- 入射光线与法线的夹角(入射光线角度)
- 入射光线自身的强度
入射光线与法线的夹角
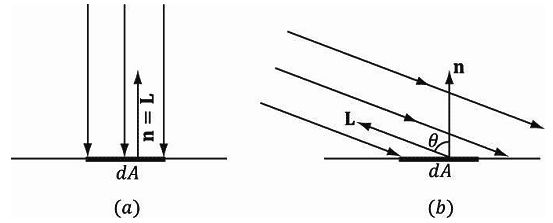
假设有一块很小的区域dA。当法线向量n与光照向量L平行时,区域dA受到的光线照射最多。随着n和L之间的夹角θ逐渐增大,区域dA*受到的光线照射量会越来越少 (因为很多光线都无法照射到dA表面上了)。冬天的时候我们觉得很冷,夏天又非常热,主要也是太阳光线与地面形成的夹角变化造成的。
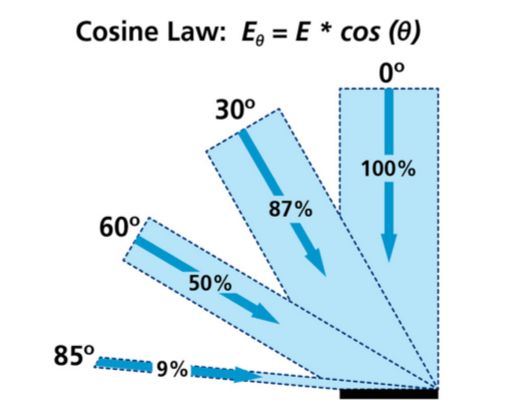
兰伯特余弦定律(Lambert Consine Law)中指出,漫反射的大小取决于表面法线和光线的夹角,当夹角越大时,漫反射分量越小,当夹角接近90度时,我们认为漫反射几乎为零。
也就是说,反射光线的强度与表面法线和光源方向之间夹角的余弦值成正比。当表面法线与光线的夹角大于90度,它们的余弦值小于0,这没有实际意义,因此将其置为0,可以用下面的公式表示
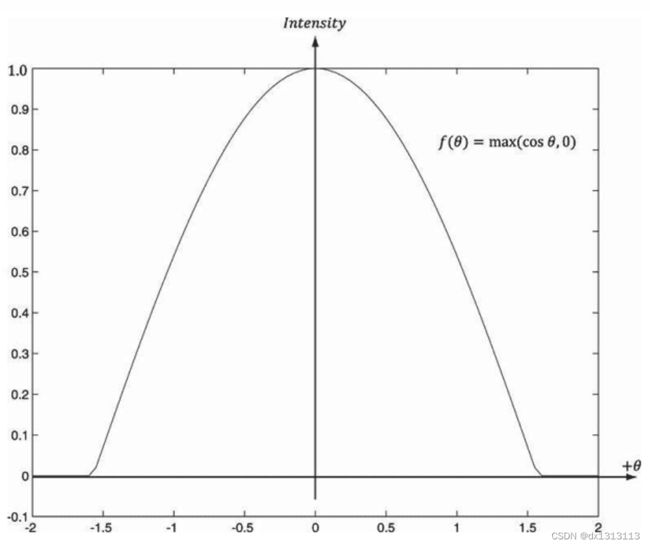
f(θ)=max(0,cosθ)=max(0,L•n)
L•n就是求L在n上的投影,下面是该函数的图像表示
入射光线强度
灯光的强度会随着距离的增加而衰减,这是显而易见的。假设我们有一个光源,在距离它单位1的圆上(图中最内圈)每一个点接收到光的强度是I。那么根据能量守恒定律,且不考虑衰减,在距离光源r位置的圆上每个点接收到光的强度就是I/r2。
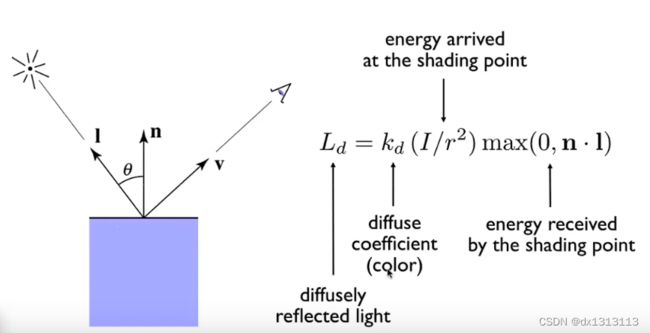
现在我们可以得出漫反射的公式:
![]()
其中Ld为漫反射光照,kd为物体表面的反射系数(reflection coefficient),I/r2是当前点接受的光照强度,max(0,L•n)是当前点接受到的能量。
什么是反射系数?
反射系数指光(入射光)投向物体时,其表面反射光的强度与入射光的强度之比值(有多少入射光能够被反射出去,其值介于0~1之间),受入射光的投射角度、强度、波长、物体表面材料的性质以及反射光的测量角度等因素影响。一般来讲,在颜色系列中,黑色的反射系数较小,为0.03,白色的反射系数较大,为0.8。(百度百科)
随着漫反射系数的增大,图像的变化如下图所示:
-
高光反射(Specular)
高光反射也称为镜面反射,若物体表面很光滑,当平行入射的光线射到这个物体表面时,仍会平行地向一个方向反射出来。
下图中一根入射光线l,照射在光滑的平面上,会沿着R方向反射,由于平面并非完全光滑,所以反射光的方向并非只有R一个点,而是R周边的一小块区域,只要眼睛(摄像机)在R附近都可以看得到,越靠近R反射光照强度越大。我们可以得出一条结论:高光反射和观察角度有关。
phong模型中认为,高光反射的强度与反射光线R和观察角度v之间夹角的余弦值成正比。计算它的强度,相当于是求向量v在R上的投影。怎么求R呢?
使用半程向量(Bisector)
计算反射光线R虽然不是很难,但还是有点繁琐,有没有其他方法计算呢?Blinn提出了一个简单的修改方法来得到类似的效果,通过对向量l和向量v取平均然后归一化得到一个新的向量h,其中h被称为半程向量(bisector),使用h与法线n点乘来计算高光,这样就可以避免计算R了。
h为半程向量:
使用半程向量计算的公式和之前类似,不过计算的时候简单了一些,具体公式如下:
![]()
参考文章
参考视频