论文阅读-利用时间序列数据增强来提高全球预测模型的准确性

Improving the Accuracy of Global Forecasting Models using Time Series Data Augmentation

全球预测模型（GFM），模型性能超过了许多最先进的单变量预测技术。

GFMs使用深度神经网络实现，特别是循环神经网络（RNN），它需要足够数量的时间序列来估计其众多模型参数。然而，许多时间序列数据库只有有限数量的时间序列。

该论文提出了一个新颖的、基于数据增强的预测框架，能够在数据不太丰富的情况下提高GFM模型的基准精度。

使用了三种时间序列增强技术：GRATIS、移动区块引导法（MBB）和动态时间扭曲arycentric平均法（DBA），来综合生成一个时间序列的集合。
使用了两种不同的方法「集合方法和迁移学习方法」，将从这些增强的时间序列中获得的知识转移到原始数据集上。

在建立GFM时，在集合方法中，我们在增强的时间序列和原始的时间序列数据集上训练一个模型；在迁移学习方法中，我们将一个预先训练好的模型调整到新的数据集。

introduction

与单独处理每个时间序列并对每个序列进行预测的单变量预测方法相比，GFMs是利用所有可用的时间序列建立的统一的预测模型。因此，GFMs能够同时学习丰富的时间序列集合中可用的共同模式，并为不断增加的时间序列量提供更好的可扩展性。GFM模型参数是使用所有可用的时间序列联合估计的，因此需要足够多的相关时间序列数据来训练。但是，在时间序列数据库受到可用时间序列数量限制的情况下，即中小尺寸的数据集，GFM可能无法充分发挥其准确性的潜力。

在缺乏足够数量的时间序列数据的情况下，GFM可能无法学习时间序列的重要特征，如季节性。
解决方案：

• 纳入关于时间序列的专家知识来补充模型训练程序
• 使用数据增强（DA）技术来人为地产生新的数据副本
  DA方法通过生成合成数据来增加可用于模型训练的观测数据的数量来解决数据稀少的问题。
• 将知识表示从背景数据集转移到目标数据集
  这个过程在机器学习文献中通常被称为迁移学习（TL）。在迁移学习中，最初使用背景或源数据集训练一个基础模型，该模型为源任务建模。然后将预训练的模型转移到具有目标任务的目标数据集上。当目标数据集比背景数据集小得多时，TL策略就特别有用。
  基于TL的方法在这些应用中的成功，主要归功于文本、图像和语音相关数据中固有的丰富数据结构。因此，预训练的模型能够捕捉到数据的共同特征，可以很容易地转移到目标任务中，同时免除了目标任务从头学习数据的一般特征。

在构建GFM时，可以通过两种不同的方式将增强的时间序列的知识转移到目标数据集：

• 通过将增强的时间序列和原始时间序列汇集在一起训练GFM
• 使用增强的时间序列预训练GFM，并由此使用TL策略将预训练模型的知识表示转移到原始数据集。

模型结构

一个基于GFM的预测框架，可用于提高数据稀疏的时间序列数据库的预测精度。其中包含RNN作为主要预测模块。在数据稀少的环境中使用DA技术来提高GFM的准确性。
其中包括三种不同的DA技术来综合生成时间序列

1. 具有多样化和可控特征的GeneRAting TIme Series（GRATIS，Kang等人，2020a）
   生成混合自回归模型来生成具有多样化和可控特征的时间序列。同时，GANs采用的竞争驱动的训练机制，允许网络产生现实的样本，类似于源数据集的DGP，GANs也可以用于生成时间序列新副本。
2. 移动块引导法（MBB，Bergmeir等人，2016）
3. 动态时间扭曲 arycentric averaging（DBA，Forestier等人，2017）

GRATIS是一个统计生成模型，可以人为地生成具有不同特征的时间序列，这些特征不一定与原始数据集的DGP相似。MBB和DBA方法的目的是生成与原始数据集的DGP相似的时间序列。

在第一种方法中，合成的时间序列与原始数据集汇集在一起，并在所有可用的时间序列中建立一个GFM（汇集策略）。在第二种方法中，使用增强的时间序列对GFM进行预训练，然后使用TL方法将预训练模型的知识表示转移到原始数据集（转移策略）。此外，使用不同的TL方案，将信息从增强的数据导入到目标数据集。

基线模型是用原始时间序列集建立的。此外，提出的预测模型使用五个时间序列数据库进行验证，包括两个竞赛数据集和三个真实世界数据集。

More recently, the application of TL methods is also gaining popularity in time series forecasting research. Ribeiro et al. (2018) introduce Hephaestus, a TL based forecasting framework for cross-building energy prediction, to improve the accuracy of energy estima- tions for new buildings with limited historical data. There, those authors propose a seasonal and trend adjusted approach that allows Hephaestus to transfer knowledge across similar buildings with different seasonal and trend profiles. The research work in Laptev et al. (2018) proposes a loss function to reconstruct the input data of the model, and thereby extract time series features using a stack of fully connected LSTM layers. Those authors show that this feature-transfer approach leads to significant accuracy improvements over the traditional TL approaches, in situations where the size of the target dataset is small. To handle time-varying properties in time series data, Ye and Dai (2018) propose a hybrid algorithm, based on TL that effectively accounts for the observations in the distant past, and leverages the latent knowledge embedded in past data to improve the forecast accu- racy. Moreover, Gupta et al. (2018) implement an RNN autoencoder architecture to extract generic sets of features from multiple clinical time series databases. Those features are then used to build simple linear models on limited labelled data for multivariate clinical time series analysis. Li et al. (2020b) first transform time series into images and use TL for image feature extraction. The extracted features are used as time series features to obtain the optimal weights of forecast combination (Kang et al., 2020a).

Forecasting Framework

该框架基于GFM的预测框架，由三层组成：1）预处理层 2）RNN训练层 3）后处理层

预处理

平均尺度转换策略
$X_{i,\text{ normalised }}=\frac{X_i}{\frac{1}{k}{\sum }_{t=1}^k{X}_{i,t}}$
其中$X_{i,\text{ normalised }}$代表第$i$个归一化的时间序列，$k$是时间序列$X_i$的观测次数，其中$i\in 1,2,d,...,N$。
然后通过对数转换来稳定时间序列的方差。它还允许我们将给定时间序列中可能存在的多重季节性和趋势性成分转换为相加的成分，为了避免零值的问题，以如下方式使用对数转换：
$X_{i,\text{ normalised \& logscaled }}=\{\begin{array}{ll}\log \left(X_{i,\text{ normalised }}\right),& \min (\mathcal{X})>0\\ \log \left(X_{i,\text{ normalised }}+1\right),& \min (\mathcal{X})=0\end{array}$
其中$\mathcal{X}$表示全部时间序列，$X_{i,\text{ normalised \& logscaled }}$是$X_i$的相应的normalized和log transformed时间序列。这里假设要预测的时间序列是非负的。

时间序列去季节化

从时间序列中提取季节性成分。

• 在第一种训练范式中，有研究者采用去离子化（DS）方法，即从时间序列中去除提取的季节性数值，然后使用剩余部分，即趋势和剩余成分，来训练NN。在这里，由于季节性成分被从时间序列中移除，在后处理阶段引入了一个额外的重季节化步骤，以预测时间序列的未来季节性价值。
• 在第二种训练模式中，季节性外生变量（SE）方法，除了时间序列的原始观测值之外，提取的季节性成分被用作外生变量输入。由于在这种方法中，时间序列没有经过季节性调整，因此在后处理阶段不需要额外的重季节化步骤。
  通过季节性趋势分解（STL）提取时间序列的季节性成分。将STL应用于归一化和对数标度的时间序列$X_i$归一化和对数标度时，其加法分解可以表述如下
  $X_{i,\text{ normalised }\&\text{ logscaled }}={\hat{S}}_i+{\hat{T}}_i+{\hat{R}}_i$
  其中，${\hat{S}}_i,{\hat{T}}_i,{\hat{R}}_i$分别是相应的季节性成分，趋势成分，以及时间序列Xi的残差成分。时间序列$X_i$的相应季节、趋势和残差分量，分别进行归一化和对数标度。

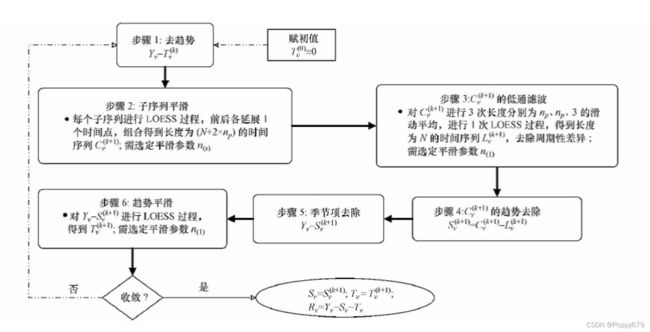
STL算法

STL(’Seasonal and Trend decomposition using Loess‘ )是以鲁棒局部加权回归作为平滑方法的时间序列分解方法。
其中Loess(locally weighted scatterplot smoothing,LOWESS or LOESS)为局部多项式回归拟合，是对两维散点图进行平滑的常用方法，它结合了传统线性回归的简洁性和非线性回归的灵活性。当要估计某个响应变量值时，先从其预测变量附近取一个数据子集，然后对该子集进行线性回归或二次回归，回归时采用加权最小二乘法，即越靠近估计点的值其权重越大，最后利用得到的局部回归模型来估计响应变量的值。用这种方法进行逐点运算得到整条拟合曲线。

Robust Loess 为鲁棒局部加权回归，具体算法可以参看之前的博文 鲁棒局部加权回归 。STL对异常点具有健壮性，仅能处理加法模式的分解，对于乘法模式需要先转换为加法模式处理最后在逆变换回去。鲁棒局部加权回归法方法的LOESS 过程和鲁棒性过程分别在STL 的内部环和外部环中嵌套实现．

残差循环神经网络

选择长短时记忆网络（LSTM）作为该模型的主要RNN架构，并实施堆叠层的设计方案来训练网络。此外，我们在堆叠结构中引入了残差连接，以解决在隐藏层数较多的情况下可能出现的梯度消失问题。

This was originally proposed by He et al. (2016) as the Residual Net (ResNet), where the authors use residual connections to accommodate substantially deeper architectures of Convolutional NNs (CNN) for image classification tasks. They also argue that learning the residual mappings is computationally easier than directly learning to fit the underlying mapping between input and output.

学习残差映射在计算上比直接学习适应输入和输出之间的基本映射要容易

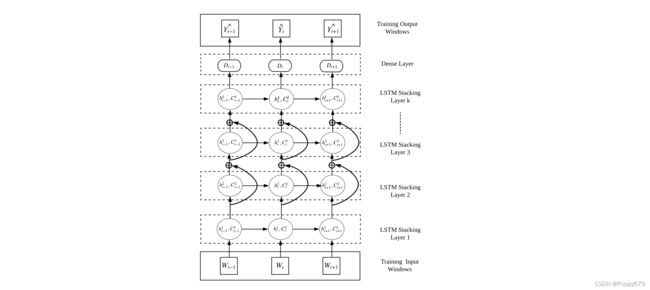
上图所示是该模型的预测架构，主要由三个部分组成：一个输入层、带有密集层的LSTM堆积层和一个输出层。以输入和输出训练窗口的形式使用预处理的时间序列，以此训练网络。这里，预处理的时间序列的值取决于训练范式，即在特定数据集中使用的DS或SE策略。这些训练窗口是通过对预处理的时间序列应用移动窗口（MW）转换策略产生的。
移动窗口（MW）转换策略中使用的多输入多输出（MIMO）原则，其中训练输出窗口的大小，$m$与预期预测范围$M$的大小相同。通过这种方式，网络被训练成一次直接预测整个预测范围${X_i}^M$，避免在每个预测步骤中积累预测误差。
此外，在这些训练窗口上，我们使用 局部归一化策略，以避免网络中可能出现的网络饱和效应。这里，用于去离子化（DS）方法的局部归一化策略与季节性外生变量（SE）方法不同。在DS方法中，使用输入窗口的最后一个值的趋势分量，而在SE方法中使用每个输入窗口的平均值。在预测架构中，$W_t\in R^n$代表时间步骤t的训练输入窗口，而$\widehat{Y_t}\in R^m$代表时间步长$t$的LSTM输出。这里, $n$表示输入窗口的大小。此外，$h_t$指的是LSTM在时间步长$t$的隐藏状态，而它在时间步长$t$的单元存储器由$C_t$给出。一个全连接层$D_t$（不包括偏置成分）被引入，用于将每个LSTM单元的输出$h_t$映射到输出窗口的维度$m$，相当于$M$。鉴于时间序列$X_i$的长度为$p$，使用预处理后的$X_i$中的一定量的$(p-m)$数据点来训练该网络，并保留预处理后$X_i$的最后一个输出窗口用于网络验证。L1-norm被用作该训练架构的主要学习目标函数，同时还有一个L2-regularisation项，以尽量减少网络中可能出现的过拟合。

后期处理

通过对 LSTM 给出的输出应用重新季节化过程和反标准化过程来计算预测框架的最终预测。仅当使用 DS 策略训练网络时才需要重新季节化。重新季节性化包括预测在预处理阶段已被删除的季节性成分，这可以通过将时间序列的最后一个季节性组成部分复制到未来，直到预期的预测范围来直接完成。 关于反标准化是通过首先添加在每个训练窗口中使用的局部规范化因子，然后使用指数函数反转对数变换。 最后将反向变换的向量乘以时间序列的平均值，这是用于归一化过程的缩放因子。

迁移学习模型结构

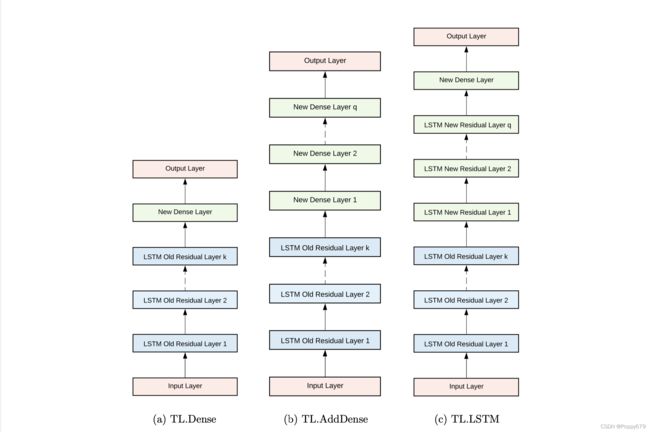
用于使用 $D_s$ 构建基础模型的层以蓝色表示，而使用 $D_t$ 构建目标模型时引入的附加层以绿色表示。
使用 LSTM 堆叠架构进行时间序列预测的三种迁移学习方案。上图显示了在研究中使用的不同 TL 方案。TL.Dense 在预训练的基础模型中引入了一个密集层，将基础模型的输出映射到 $D_t$ 中输出窗口的维度。 TL.AddDense 将一定数量的 $q$个密集层添加到预训练的基础模型中。最后，在 TL.LSTM 中，将 $q$个带有密集层的 LSTM 残差层引入到基础模型中。其中，假设基础模型中存在 $k$ 个残差层。
通过更改架构中可训练参数的总数进一步引入了这些 TL 方案的变体。这里是通过训练网络来实现这一点，仅使用新引入的隐藏层的参数，同时冻结预训练基础模型的隐藏层。基于这些 TL 方案，TL 架构定义如下：
**TL.Dense.Freeze：**使用TL.Dense方案的TL架构，同时冻结预训练模型的初始层，只训练新添加的层。
**TL.Dense.Retrain：**使用TL.Dense方案的TL架构，同时重新训练预训练模型的初始层和新增层。
**TL.AddDense.Freeze：**使用TL.AddDense方案的TL架构，同时冻结预训练模型的初始层，只训练新添加的层。
**TL.AddDense.Retrain：**使用TL.AddDense方案的TL架构，同时重新训练预训练模型的初始层和新添加的层。
**TL.LSTM.Freeze：**使用TL.LSTM方案的TL架构，同时冻结预训练模型的初始层，只训练新添加的层。
**TL.LSTM.Retrain：**TL架构，使用TL.LSTMscheme，同时重新训练预训练模型的初始层和新添加的层。
这里，TL.Dense.Retrain、TL.AddDense.Retrain 和 TL.LSTM.Retrain 重新训练模型的所有层，而 TL.Dense.Freeze、TL.AddDense.Freeze 和 TL.LSTM.Freeze仅将新添加的层重新训练到模型中。此外，这里遵循 Transductive TL 方法(源域和目标域不同，学习任务相同)，其中 $T_t$ 和 $T_s$ 相同，即时间序列预测，但用于训练任务的数据集是不同的。

时间序列增强

GRATIS

这里使用一种统计生成模型GRATIS来创建具有不同特征的新时间序列。 GRATIS 采用混合自回归 (MAR) 模型来生成一组具有不同特征的新时间序列。在统计建模中，MAR 模型通常用于对具有多种统计分布和不同特征的群体进行建模，方法是使用模型的混合而不是单个自回归 (AR) 模型。在混合 AR 模型中，每个 AR 过程的系数都是从高斯分布中选择的。然后，混合权重矩阵提供每个 AR 模型对生成的时间序列的贡献。

相关实验设计

GRATIS 与第二种方法（转移策略）一起使用，该方法使用从 GRATIS 生成的时间序列预训练 GFM 模型，然后将知识转移到目标数据集。如果两个连接的时间序列数据集彼此差异太大，则 GFM 的准确性会降低，所以来自 GRATIS 方法的增强时间序列可能不适用于第一种TL方法，池化策略。

MBB

MBB 是时间序列预测中常用的引导技术，这里使用 MBB 技术进行时间序列增强。

相关实验设计

为了生成时间序列的多个副本，首先使用 STL 来提取并随后删除时间序列的季节性和趋势分量。接下来，将 MBB 技术应用于时间序列的其余部分，即季节性和趋势调整序列，以生成多个版本的残差分量。最后，自举残差分量与相应的季节和趋势一起加回以生成时间序列的新自举(Bootstrapping)版本。由于在引导过程中使用原始观察，人工生成的数据与原始训练数据集的分布非常相似，即具有相似的季节性和趋势。

动态时间扭曲重心平均 (DBA)

与 MBB 将 bootstrapping 程序分别应用于每个时间序列不同，DBA 方法将一组时间序列平均以生成新的合成样本，从而在生成新序列时能够混合不同时间序列的特征，从而更好地考虑一组时间序列中的全局特征。 DBA 方法允许在计算每个时间序列对最终生成的时间序列的贡献时在模型中进行加权平均。
目前有三种方法来确定与数据集的时间序列相关的权重，即：平均所有 (AA)、平均选择 (AS) 和平均选择距离 (ASD)。这里使用 ASD 作为主要平均方法。由于原始数据集的特征用于生成时间序列，类似于 MBB，DBA 也可以归类为生成类似于原始训练数据集的增强序列的 DA 技术。