机器学习笔记（8）——数据预处理&特征工程

机器学习笔记（8）——数据预处理&特征工程

本文部分/全部图片与文字来源网络或学术论文，仅供学习使用，持续修改完善中。​​​​​​​

目录

机器学习笔记（8）——数据预处理&特征工程

1. 数据预处理

1.1. 数据无纲量化

（1）数据归一化：

（2）数据标准化：

（3）选择归一化还是标准化？

1.2.缺失值

1.3. 处理分类型特征

1.4.处理连续型特征：二值化与分段

2. 特征选择（特征工程）

2.1.过滤法fliter

2.1.1方差过滤

2.1.2卡方过滤

2.1.4F检验过滤

2.1.5互信息法过滤

2.2.embedded嵌入法

2.3.wrapper包装法

小结

---

明确：数据挖掘的一般流程（5步）

获取数据——>数据预处理——>特征选择——>建模——>验证模型效果

1. 数据预处理

数据预处理：是从数据中检测，纠正或删除损坏，不准确或不适用于模型的记录的过程。

可能面对的问题有：数据类型不同，比如有的是文字，有的是数字，有的含时间序列，有的连续，有的间断。也可能，数据的质量不行，有噪声，有异常，有缺失，数据出错，量纲不一，有重复，数据是偏态，数据量太大或太小。

数据预处理的目的：让数据适应模型，匹配模型的需求。

1.1. 数据无纲量化

线性的无量纲化包括中心化（Zero-centered或者Meansubtraction）处理和缩放处理（Scale）。

1. 中心化的本质是让所有记录减去一个固定值，即让数据样本数据平移到某个位置。
2. 缩放的本质是通过除以一个固定值，将数据固定在某个范围之中，取对数也算是一种缩放处理。

（1）数据归一化：

数据归一化(Normalization，又称Min-Max Scaling)：当数据(x)按照最小值中心化后，再按极差（最大值 - 最小值）缩放，数据移动了最小值个单位，并且会被收敛到[0,1]之间，而这个过程，就叫做数据归一化。归一化之后数据服从正态分布。

from sklearn.preprocessing import MinMaxScaler
 
data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]
 
import pandas as pd
pd.DataFrame(data)
 
#实现归一化
scaler = MinMaxScaler()                             #实例化
scaler = scaler.fit(data)                           #fit，在这里本质是生成min(x)和max(x)
result = scaler.transform(data)                     #通过接口导出结果
result

result_ = scaler.fit_transform(data)                #训练和导出结果一步达成
 
scaler.inverse_transform(result)                    #将归一化后的结果逆转
 
#使用MinMaxScaler的参数feature_range实现将数据归一化到[0,1]以外的范围中
data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]
scaler = MinMaxScaler(feature_range=[5,10])         #依然实例化
result = scaler.fit_transform(data)                 #fit_transform一步导出结果
result
 
#当X中的特征数量非常多的时候，fit会报错并表示，数据量太大了我计算不了
#此时使用partial_fit作为训练接口
#scaler = scaler.partial_fit(data)

#使用numpy来实现归一化
import numpy as np
X = np.array([[-1, 2], [-0.5, 6], [0, 10], [1, 18]])
 
#归一化
X_nor = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_nor
 
#逆转归一化
X_returned = X_nor * (X.max(axis=0) - X.min(axis=0)) + X.min(axis=0)
X_returned

（2）数据标准化：

当数据(x)按均值(μ)中心化后，再按标准差(σ)缩放，数据就会服从为均值为0，方差为1的正态分布（即标准正态分布），这个过程就叫做数据标准化。

from sklearn.preprocessing import StandardScaler
data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]
 
scaler = StandardScaler()                           #实例化
scaler.fit(data)                                    #fit，本质是生成均值和方差
 
scaler.mean_                                        #查看均值的属性mean_
scaler.var_                                         #查看方差的属性var_
 
x_std = scaler.transform(data)                      #通过接口导出结果
 
x_std.mean()                                        #导出的结果是一个数组，用mean()查看均值
x_std.std()                                         #用std()查看方差
 
scaler.fit_transform(data)                          #使用fit_transform(data)一步达成结果
 
scaler.inverse_transform(x_std)                     #使用inverse_transform逆转标准化

对于StandardScaler和MinMaxScaler来说，空值NaN会被当做是缺失值，在fit的时候忽略，在transform的时候保持缺失NaN的状态显示。并且，尽管去量纲化过程不是具体的算法，但在fit接口中，依然只允许导入至少二维数组，一维数组导入会报错。

（3）选择归一化还是标准化？

大多数机器学习算法中，会选择StandardScaler来进行特征缩放，因为MinMaxScaler对异常值非常敏感。在PCA，聚类，逻辑回归，支持向量机，神经网络这些算法中，StandardScaler往往是最好的选择。

MinMaxScaler在不涉及距离度量、梯度、协方差计算以及数据需要被压缩到特定区间时使用广泛，比如数字图像处理中量化像素强度时，都会使用MinMaxScaler将数据压缩于[0,1]区间之中。
 

1.2.缺失值

import pandas as pd
data_ = pd.read_csv(r".\Narrativedata.csv"
                   ,index_col=0
                  )#index_col=0将第0列作为索引，不写则认为第0列为特征

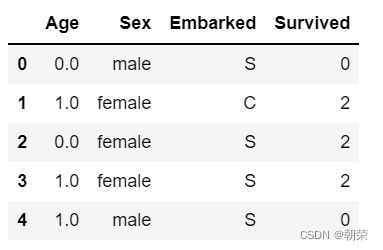
data_.head()
 
data_.loc[:,"Age"] = data_.loc[:,"Age"].fillna(data_.loc[:,"Age"].median())
#.fillna 在DataFrame里面直接进行填补
 
data_.dropna(axis=0,inplace=True)
#.dropna(axis=0)删除所有有缺失值的行，.dropna(axis=1)删除所有有缺失值的列
#参数inplace，为True表示在原数据集上进行修改，为False表示生成一个复制对象，不修改原数据，默认False
# _data_ = data_.drop(axis=0,inplace=False)

from sklearn.preprocessing import LabelEncoder
 
y = data_.iloc[:,-1]                         #要输入的是标签，不是特征矩阵，所以允许一维
 
le = LabelEncoder()                         #实例化
le = le.fit(y)                              #导入数据
label = le.transform(y)                     #transform接口调取结果
 
le.classes_                                 #属性.classes_查看标签中究竟有多少类别
label                                       #查看获取的结果label
 
le.fit_transform(y)                         #也可以直接fit_transform一步到位
 
le.inverse_transform(label)                 #使用inverse_transform可以逆转

1.3. 处理分类型特征

(1)为了让数据适应算法和库，有时必须将数据进行编码，即将文字型数据转换为数值型。

from sklearn.preprocessing import LabelEncoder
 
y = data.iloc[:,-1]                         #要输入的是标签，不是特征矩阵，所以允许一维
 
le = LabelEncoder()                         #实例化
le = le.fit(y)                              #导入数据
label = le.transform(y)                     #transform接口调取结果
 
le.classes_                                 #属性.classes_查看标签中究竟有多少类别
label                                       #查看获取的结果label
 
le.fit_transform(y)                         #也可以直接fit_transform一步到位
 
le.inverse_transform(label)                 #使用inverse_transform可以逆转

data.iloc[:,-1] = label                     #让标签等于我们运行出来的结果
 
data.head()
 
#也可以写为
from sklearn.preprocessing import LabelEncoder
data.iloc[:,-1] = LabelEncoder().fit_transform(data.iloc[:,-1])

1.4.处理连续型特征：二值化与分段

根据阈值将数据二值化（将特征值设置为0或1），用于处理连续型变量。大于阈值的值映射为1，而小于或等于阈值的值映射为0。

#将年龄二值化
 
data_2 = data.copy()
 
from sklearn.preprocessing import Binarizer
X = data_2.iloc[:,0].values.reshape(-1,1)               #类为特征专用，所以不能使用一维数组
transformer = Binarizer(threshold=30).fit_transform(X)
 
data_2.iloc[:,0] = transformer
data_2.head()

将连续型变量划分为分类变量的类，能够将连续型变量排序后按顺序分箱后编码。

from sklearn.preprocessing import KBinsDiscretizer
 
X = data.iloc[:,0].values.reshape(-1,1) 
est = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='uniform')
est.fit_transform(X)
 
#查看转换后分的箱：变成了一列中的三箱
set(est.fit_transform(X).ravel())
 
est = KBinsDiscretizer(n_bins=3, encode='onehot', strategy='uniform')
#查看转换后分的箱：变成了哑变量
est.fit_transform(X).toarray()

2. 特征选择（特征工程）

特征工程：是将原始数据转换为更能代表预测模型的潜在问题的特征的过程，可以通过挑选最相关的特征，提取特征以及创造特征来实现。；其中创造特征又经常以降维算法的方式实现。

可能面对的问题有：特征之间有相关性，特征和标签无关，特征太多或太小，或者干脆就无法表现出应有的数 据现象或无法展示数据的真实面貌。

特征工程的目的：1) 降低计算成本，2) 提升模型上限。 

特征选择完全独立于任何机器学习算法。它是根据各种统计检验中的分数以及相关性的各项指标来选择特征。
 

2.1.过滤法fliter

2.1.1方差过滤

方差阈值过滤：如一个特征本身的方差很小，就表示样本在这个特征上基本没有差异，可能特征中的大多数值都一样，甚至整个特征的取值都相同，那这个特征对于样本区分没有什么作用。所以无论接下来的特征工程要做什么，都要优先消除方差为0的特征。

#去掉方差为0的特征
from sklearn.feature_selection import VarianceThreshold
selector = VarianceThreshold()                      #实例化，不填参数默认方差为0
X_var0 = selector.fit_transform(X)                  #获取删除不合格特征之后的新特征矩阵
 
#也可以直接写成 X = VairanceThreshold().fit_transform(X)
 
X_var0.shape#(42000, 708)
pd.DataFrame(X_var0).head()

#根据阈值，删除阈值一下的所有特征
import numpy as np
# X.var()#每一列的方差
X_fsvar = VarianceThreshold(np.median(X.var().values)).fit_transform(X)
 
print(X.var().values.shape)
 
print(np.median(X.var().values))
 
X_fsvar.shape#(42000, 392)

#若特征是伯努利随机变量，假设p=0.8，即二分类特征中某种分类占到80%以上的时候删除特征
X_bvar = VarianceThreshold(.8 * (1 - .8)).fit_transform(X)
X_bvar.shape

方差过滤的效果：

1. 最近邻算法KNN，单棵决策树，支持向量机SVM，神经网络，回归算法，都需要遍历特征或升维来进行运算，所以他们本身的运算量就很大，需要的时间就很长，因此方差过滤这样的特征选择对他们来说就尤为重要。
2. 但对于不需要遍历特征的算法，比如随机森林，它随机选取特征进行分枝，本身运算就非常快速，因此特征选择对它来说效果平平。
3. 过滤法的主要对象是：需要遍历特征或升维的算法们，而过滤法的主要目的是：在维持算法表现的前提下，帮助算法们降低计算成本。
    

 选取超参数threshold：每个数据集不一样，只能自己去尝试。这里的方差阈值，其实相当于是一个超参数，要选定最优的超参数，我们可以画学习曲线，找模型效果最好的点。

2.1.2卡方过滤

卡方过滤是专门针对离散型标签（即分类问题）的相关性过滤。卡方检验类feature_selection.chi2计算每个非负特征和标签之间的卡方统计量，并依照卡方统计量由高到低为特征排名。再结合feature_selection.SelectKBest这个可以输入”评分标准“来选出前K个分数最高的特征的类，我们可以借此除去最可能独立于标签，与我们分类目的无关的特征。
如果卡方检验检测到某个特征中所有的值都相同，会提示我们使用方差先进行方差过滤。
可以使用threshold=中位数时完成的方差过滤的数据来做卡方检验（如果方差过滤后模型的表现反而降低了，那我们就不会使用方差过滤后的数据，而是使用原数据）
 

from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
 
#假设在这里我一直我需要300个特征
X_fschi = SelectKBest(chi2, k=300).fit_transform(X_fsvar, y)
X_fschi.shape

确定超惨k：数据量很大，模型很复杂的时候，我们也许不能先去跑一遍模型看看效果，而是希望最开始就能够选择一个最优的超参数k。因此需要绘制学习曲线。

#======【TIME WARNING: 5 mins】======#
 
%matplotlib inline
import matplotlib.pyplot as plt
 
score = []
for i in range(390,200,-10):
    X_fschi = SelectKBest(chi2, k=i).fit_transform(X_fsvar, y)
    once = cross_val_score(RFC(n_estimators=10,random_state=0),X_fschi,y,cv=5).mean()
    score.append(once)
plt.plot(range(390,200,-10),score)
plt.show()

卡方检验的本质是推测两组数据之间的差异，其检验的原假设是”两组数据是相互独立的”。卡方检验返回卡方值和P值两个统计量，其中卡方值很难界定有效的范围，而p值，我们一般使用0.01或0.05作为显著性水平，即p值判断的边界。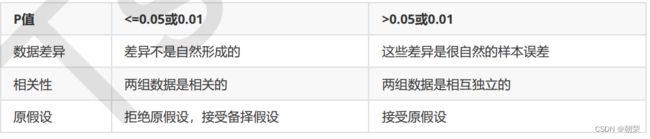

 从特征工程的角度，我们希望选取卡方值很大，p值小于0.05的特征，即和标签是相关联的特征。而调用SelectKBest之前，我们可以直接从chi2实例化后的模型中获得各个特征所对应的卡方值和P值。

chivalue, pvalues_chi = chi2(X_fsvar,y)
 
chivalue
 
pvalues_chi
 
#k取多少？我们想要消除所有p值大于设定值，比如0.05或0.01的特征：
k = chivalue.shape[0] - (pvalues_chi > 0.05).sum()
 
#X_fschi = SelectKBest(chi2, k=填写具体的k).fit_transform(X_fsvar, y)
#cross_val_score(RFC(n_estimators=10,random_state=0),X_fschi,y,cv=5).mean()

2.1.4F检验过滤

F检验，又称ANOVA，方差齐性检验，是用来捕捉每个特征与标签之间的线性关系的过滤方法。它即可以做回归也可以做分类，因此包含feature_selection.f_classif（F检验分类）和feature_selection.f_regression（F检验回归）两个类。

F检验的本质是寻找两组数据之间的线性关系，其原假设是”数据不存在显著的线性关系“。它返回F值和p值两个统计量。和卡方过滤一样，我们希望选取p值小于0.05或0.01的特征，这些特征与标签时显著线性相关的，而p值大于0.05或0.01的特征则被我们认为是和标签没有显著线性关系的特征，应该被删除。

from sklearn.feature_selection import f_classif
 
F, pvalues_f = f_classif(X_fsvar,y)
 
pvalues_f
 
k = F.shape[0] - (pvalues_f > 0.05).sum()
 
#X_fsF = SelectKBest(f_classif, k=填写具体的k).fit_transform(X_fsvar, y)
#cross_val_score(RFC(n_estimators=10,random_state=0),X_fsF,y,cv=5).mean()

2.1.5互信息法过滤

互信息法是用来捕捉每个特征与标签之间的任意关系（包括线性和非线性关系）的过滤方法。和F检验相似，它既可以做回归也可以做分类，并且包含两个类feature_selection.mutual_info_classif（互信息分类）和feature_selection.mutual_info_regression（互信息回归）。这两个类的用法和参数都和F检验一模一样，不过互信息法比F检验更加强大，F检验只能够找出线性关系，而互信息法可以找出任意关系。

互信息法不返回p值或F值类似的统计量，它返回“每个特征与目标之间的互信息量的估计”，这个估计量在[0,1]之间取值，为0则表示两个变量独立，为1则表示两个变量完全相关。

from sklearn.feature_selection import mutual_info_classif as MIC
 
result = MIC(X_fsvar,y)
 
k = result.shape[0] - sum(result <= 0)
 
#X_fsmic = SelectKBest(MIC, k=填写具体的k).fit_transform(X_fsvar, y)
#cross_val_score(RFC(n_estimators=10,random_state=0),X_fsmic,y,cv=5).mean()

sklearn中的过滤方法小结：

类	说明	超参数的选择
VarianceThreshold	方差过滤，可输入方差阈值，返回方差大于 阈值的新特征矩阵	看具体数据究竟是含有更多噪 声还是更多有效特征 一般就使用0或1来筛选 也可以画学习曲线或取中位数 跑模型来帮助确认
SelectKBest	用来选取K个统计量结果最佳的特征，生成 符合统计量要求的新特征矩阵	看配合使用的统计量
chi2	卡方检验，专用于分类算法，捕捉相关性	追求p小于显著性水平的特征
f_classif	F检验分类，只能捕捉线性相关性 要求数据服从正态分布	追求p小于显著性水平的特征
f_regression	F检验回归，只能捕捉线性相关性 要求数据服从正态分布	追求p小于显著性水平的特征
mutual_info_classif	互信息分类，可以捕捉任何相关性 不能用于稀疏矩阵	追求互信息估计大于0的特征
mutual_info_regression	互信息回归，可以捕捉任何相关性 不能用于稀疏矩阵	追求互信息估计大于0的特征

2.2.embedded嵌入法

嵌入法是一种让算法自己决定使用哪些特征的方法，即特征选择和算法训练同时进行。在使用嵌入法时，先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据权值系数从大到小选择特征。（参见西瓜书的介绍）

相比于过滤法，嵌入法的结果会更加精确到模型的效用本身，对于提高模型效力有更好的效果。并且，由于考虑特征对模型的贡献，因此无关的特征（需要相关性过滤的特征）和无区分度的特征（需要方差过滤的特征）都会因为缺乏对模型的贡献而被删除掉，可谓是过滤法的进化版。

class sklearn.feature_selection.SelectFromModel (estimator, threshold=None, prefit=False, norm_order=1,max_features=None)

参数	说明
estimator	使用的模型评估器，只要是带feature_importances_或者coef_属性，或带有l1和l2惩罚 项的模型都可以使用
threshold	特征重要性的阈值，重要性低于这个阈值的特征都将被删除
prefit	默认False，判断是否将实例化后的模型直接传递给构造函数。如果为True，则必须直接 调用fit和transform，不能使用fit_transform，并且SelectFromModel不能与 cross_val_score，GridSearchCV和克隆估计器的类似实用程序一起使用。
norm_order	k可输入非零整数，正无穷，负无穷，默认值为1 在评估器的coef_属性高于一维的情况下，用于过滤低于阈值的系数的向量的范数的阶 数。
max_features	在阈值设定下，要选择的最大特征数。要禁用阈值并仅根据max_features选择，请设置 threshold = -np.inf

from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier as RFC
 
RFC_ = RFC(n_estimators =10,random_state=0)
 
X_embedded = SelectFromModel(RFC_,threshold=0.005).fit_transform(X,y)
 
#在这里我只想取出来有限的特征。0.005这个阈值对于有780个特征的数据来说，是非常高的阈值，因为平均每个特征
# 只能够分到大约0.001的feature_importances_
 
X_embedded.shape
 
#模型的维度明显被降低了
#同样的，我们也可以画学习曲线来找最佳阈值
 
#======【TIME WARNING：10 mins】======#
 
import numpy as np
import matplotlib.pyplot as plt
 
RFC_.fit(X,y).feature_importances_
 
threshold = np.linspace(0,(RFC_.fit(X,y).feature_importances_).max(),20)
 
score = []
for i in threshold:
    X_embedded = SelectFromModel(RFC_,threshold=i).fit_transform(X,y)
    once = cross_val_score(RFC_,X_embedded,y,cv=5).mean()
    score.append(once)
plt.plot(threshold,score)
plt.show()

2.3.wrapper包装法

包装法也是一个特征选择和算法训练同时进行的方法，与嵌入法十分相似，它也是依赖于算法自身的选择，比如coef_属性或feature_importances_属性来完成特征选择。

但不同的是，我们往往使用一个目标函数作为黑盒来帮助我们选取特征，而不是自己输入某个评估指标或统计量的阈值。包装法在初始特征集上训练评估器，并且通过coef_属性或通过feature_importances_属性获得每个特征的重要性。

然后，从当前的一组特征中修剪最不重要的特征。在修剪的集合上递归地重复该过程，直到最终到达所需数量的要选择的特征。区别于过滤法和嵌入法的一次训练解决所有问题，包装法要使用特征子集进行多次训练，因此它所需要的计算成本是最高的。

class sklearn.feature_selection.RFE (estimator, n_features_to_select=None, step=1, verbose=0)
 

#======【TIME WARNING: 15 mins】======#
 
score = []
for i in range(1,751,50):
    X_wrapper = RFE(RFC_,n_features_to_select=i, step=50).fit_transform(X,y)
    once = cross_val_score(RFC_,X_wrapper,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(1,751,50),score)
plt.xticks(range(1,751,50))
plt.show()

小结

过滤法更快速，但更粗糙。包装法和嵌入法更精确，比较适合具体到算法去调整，但计算量比较大，运行时间长。

当数据量很大的时候，优先使用方差过滤和互信息法调整，再上其他特征选择方法。

使用逻辑回归时，优先使用嵌入法。

使用支持向量机时，优先使用包装法