计算机组成原理13----浮点运算和算术逻辑单元ALU
在计算机中浮点数是如何完成加减乘除运算的
浮点数的定义及表示
![]()
S为尾数,r为基值,j为阶码
在计算机寄存器中大致存放示意如下所示
![]()
浮点加减运算
当基值r=2时为例
浮点加减运算步骤如下:
对阶 尾数求和 规格化 舍入 溢出判断
对阶
使两操作数小数点位置对齐,即两数阶码相等
首先求出阶差,然后按照小阶向大阶看齐的方式,将小阶的阶码变大,尾数右移变小,此过程可能会发生精度损失。
尾数求和
将对阶后的两个尾数按定点运算来进行计算
规格化
规格化数的定义
从形式上看,对于原码规格化数的尾数最高位为1
可知对于原码来说,最高位为1,对于补码来说,尾数最高位和符号位不同即为规格化数。
特别地,
当S=-1/2时,S真=-0.10000 S原=1.10000 S补=1.10000 即S补不是规格化数
当S=-1时, S补=1.0000 S补为规格化数
左规
尾数过小,尾数左移一位 阶码减一 直到数符位和尾数最高位不一致
右规
尾数过大,尾数溢出时,尾数右移 阶码加一
舍入
在对阶和右规过程中,可能会将尾数低位丢失,精度丧失
0舍1入法 尾数右移时,被移除的数为最高位为0时,尾数低位补0 被移除的数最高位为1时,尾数补1
恒置1法 尾数右移时,低位补1
溢出判断
尾数求和,右规之后,根据阶码来判断是否发生溢出
假定机器数为补码形式,尾数规格化,阶符2位,阶码数值7位,数符2位,尾数数值n位,表示数据如下
当阶码出现10,....时,说明出现下溢,此时按机器零来处理
当阶码出现01,......时,说明出现上溢,需进行中断溢出处理
浮点数的乘除运算可以转换为尾部部分和阶码部分的乘除运算,每一部分可以看成定点数来运算,但是要考虑对阶和规格化问题。
算术逻辑单元ALU
能够同时完成算术运算和逻辑运算的部件
ALU基本电路示意如下:
Ai Bi为输入 Ki为控制信号 Fi为输出函数 Ki的不同取值可以控制电路完成不同的算术或者逻辑运算
ALU为组合逻辑电路 输入A,B需要与锁存器连接,在运算过程中保持锁存器不变,输出结果需要保存在寄存器中
快速进位链
74181是能够完成4位二进制代码的ALU,如果需要完成64位二进制数据的加法运算,需要将多个全加器进行级联组成新的全加器,此时进位速度对于运算结果影响最大。
并行加法器
n+1个全加器组成一个n+1位并行加法器
对于和Si与Ai,Bi和Ci-1有关,可以由数字电路原理得到
对于每一位的进位Ci与Ai,Bi和Ci-1有关,只需要三者中1的个数大于2就可以产生进位
令di=AiBi 本地进位 ti=Ai+BI为传递条件,
串行进位链
并行加法器中的进位信号采用串行传递
以四位并行加法器为例,每一位进位信号表达式为
其中di,ti为本地进位和传递条件,由上述给出
则四位并行加法器进位链可以由8个与非门来实现
假定与非门的延时为ty,则N位加法器总延时为2Nty
并行进位链
加法器中额进位信号同时产生
四位加法器进位信号
因此可以设计电路来实现进位同时产生
与或非门延迟时间为1.5ty,与非门为ty,则总延时为2.5ty
如果N位加法器进位信号全部同时产生,可知表达式复杂,实现困难。
单重分组跳跃进位
将N位全加器分成若干小组,小组内进位同时产生,小组与小组之间串行进位
第四小组采用并行进位链,可知2.5ty可以产生C0-C3进位,经10ty可以产生所有进位
双重分组跳跃进位
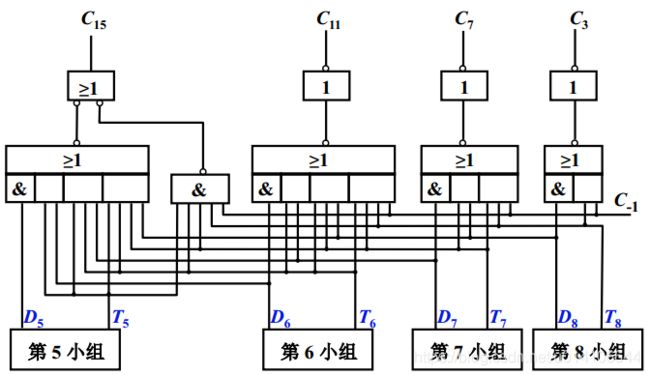
N位全加器分成若干大组,每个大组包含若干小组,每个大组内各个小组进位同时产生,大组之间串行进位
大组进位分析
考虑第二大组的进位电路
第8小组
D8为小组本地进位与外来进位无关,T8为小组传递条件 与外来进位无关
同理
因此可以得到第2大组内的进位电路
如果D5-D8 T5-T8 C-1已经产生,则经过2.5ty可以同时产生C3,C7,C11,C15进位信号
小组进位信号分析
以第8小组为例:
此时第8小组可以产生C0-C2 D8 T8进位信号,进位延迟2.5ty
第2大组进位链产生
如果 di ti C-1产生,
经过2.5ty,可以产生C0-C2 D5-D8 T5-T8
经5ty,产生C15,C11,C7,C3
经7.5ty,产生C4-C6 C8-C10 C12-C14
第一第二大组进位产生
2.5ty C0-C2 D1-D8 T1-T8
5ty C3 C7 C11 C15
7.5ty C16-C18 C12-C14 C8-C10 C4-C6 C19 C23 C27 C31
10ty C20-C22 C24-C26 C28-C30