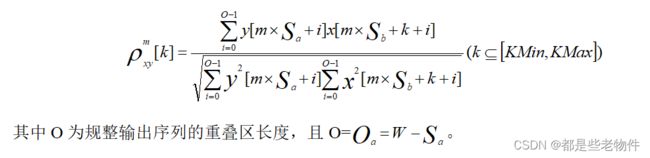基于SOLA算法的变声实例

摘  要

语音信号中有各种各样的信息，主要载有语音内容信息(What was said ?)、说话人特征信息(who said it ?)以及说话环境信息(where it was said ?)。说话人特征描述了与说话人身份相关的声音方面特征，而与具体内容信息和说话环境无关。语音转换的任务就是就是要改变说话人特征，而其它方面的信息保留不变。

本文的主要步骤有：

• 基于计算机模拟信号的采样。计算机内的声音传感器感知外界的声音播放源，收集声音模拟信号，模拟信号经过A/D转换器，以量化后的二进制数存储在计算机中，该二进制数的位数越高，采样精度也越高。
• 对声音特性的描述分析。声音主要由音质决定的，音质包含了音高、音色、音量三个主要方面。音高影响着声音的响度；音色决定着声音的表现；音频概述着声音的尖锐或浑浊程度。
• 深刻理解SOLA（Synchronized overlap-add）重叠相加算法的内涵及原理，并将其充分利用在声音变速的实现上。
• 声音在时域与频域上的变换。根据傅里叶中信号组成的概念，对于声音信号可以进行傅里叶级数展开(在计算机处理中即求其的DFT)。得到其频谱后，观察音高，音调，泛音等特性，通过一系列频谱变换的手段，如上采样、下采样、线性插值、或频谱搬移，改变其频谱结构，进而改变声音信号。
• 用MATLAB编程实现整个功能。

关键词：DFT/FFT；上采样；下采样；SOLA算法；音质；

引言

目前，说话人语音转换技术取得了一定的成果，无论是主观测试还是客观测试，转换语音相比源语音都更接近于目标语音，但是这种转换技术还是一项很不成熟的技术，还有很多问题需要解决。这是一门基于统计与大数据的技术，需要大量的声音特征信号作为基础。而在没有大量数据支持的情况下，我们只能很笼统地去转换声音，在转换成的每一类声音中将无法继续细分。另外很多的声音经过转换后会产生明显的失真与缺失，这将影响着转换的质量。其中语音时间规整技术和语音变调技术是两大很重要的课题，是语音信号处理的重要组成部分。

 

    声音的频带与特性

      声音的频带划分

据我们常规的定义，频率在250Hz以下为低频，频率在500-2kHz为中频，而高频则是2kHZ-16kHZ。而人能听到的最高声音频率为20kHz。

20Hz--60Hz部分。这一段提升能给音乐强有力的感觉，给人很响的感觉，如雷声。如果提升过高，则又会混浊不清，造成清晰度不佳，特别是低频响应差和低频过重的音响设备。

60Hz--250Hz部分。这段是音乐的低频结构，它们包含了节奏部分的基础音，包括基音、节奏音的主音。它和高中音的比例构成了音色结构的平衡特性。提升这一段可使声音丰满，过度提升会发出隆隆声，衰减此频段和高中音段会使声音单薄。

250Hz--4KHz部分。这段包含了大多数乐器的低频谐波，同时影响人声和乐器等声音的清晰度，调整时要配合前面低音的设置，否则音质会变的很沉闷。如果提升过多会使声音像电话里的声音；如把600Hz和1kHz过度提升会使声音像喇叭的声音；如把3KHz提升过多会掩蔽说话的识别音，即口齿不清，并使唇音“m、b、v”难以分辨；如把1kHz和3kHz过分提升会使声音具有金属感。由于人耳对这一频段比较敏感，通常不调节这一段，过分提升这一段会使听觉疲劳。

4kHz--5KHz部分。这是影响临场感（距离感）的频段。提升这一频段，使人感觉声源与听者的距离显得稍近了一些；衰减则就会使声音的距离感变远；如果在5KHz左右提升6dB，则会使整个混合声音的声功率提升3dB。

6kHz--16kHz部分。这一频段控制着音色的明亮度，宏亮度和清晰度。一般来说提升这部分使声音洪亮，但不清晰，还可能会引起齿音过重；衰减这部分使声音变得清晰，可音质又略显单薄。该频段适合还原人声。

低频部分幅度最突出的频率通常定义成基频，基频整数倍的频率成分为谐波。此外声音一般在频谱上有两个或以上的共振峰(共振峰指的是频谱上能量较为集中的频带）,在声学模型上，这些共振峰就是发声腔体的谐振频率区。我们可以把人的发声腔体比作一个个不同频率的带通谐振滤波器，在不断的振动中对于某些频率成分衰减，某些频率成分增强，增强的即为共振峰。共振峰很大程度的决定了一个声音的音质。

 

声音的特性

声音的特性主要由音高、音色、音量决定。

声音频率的高低叫做音高。表示人的听觉分辨一个声音的调子高低的程度。音高主要由声音的频率决定，同时也与声音强度有关。对一定强度的纯音，音高随频率的升降而升降；对一定频率的纯音、低频纯音的音高随声强增加而下降，高频纯音的音高却随强度增加而上升。高频谐波多的声音表现得很尖锐，低频部分多的声音表现得很浑厚。

音量，是指各种音调高低不同的声音，即音的高度，音的基本特征的一种。音量值大的声音洪亮，音量值低的声音低沉。

音色是指不同声音表现在波形方面总是有与众不同的特性，不同的物体振动都有不同的特点。音色主要由声音的泛音部分决定，对于不同音色的声音而言，它们泛音的起伏波动是不同的。泛音可以理解成对声音信号进行傅里叶分解后的谐波成分。对于纯音来说，是只有基频部分而无泛音部分的。

 

设计原理

采样分析

人能感知的最高声音频率为20kHz，故我们得到的声音采样信号在频谱上只要能包含0～20kHZ范围内的频率信息就行了。根据采样定理，采样后的信号在频谱上是以采样频率进行周期拓扑的，且采样频率应为最高频率的两倍才能很好的保存和复原声音信号。

从信号的傅里叶级数组成上来看，声音信号是由不同频率的正余弦信号组成，每一种组成信号在一次振动中至少要有两次采样，分别在高电平和低电平区域，人能感知的声音频率最高为20KHZ，所以为了在20KHZ内的每一个信号的每一次振动中能取到至少两个点，一般把采样率设置为40KHZ ,这是不同于从频谱角度上的分析。

为了对原始采样信号进行变调处理，通常会进行第二次采样，该操作称为重采样。

重采样可细分为上采样、下采样以及线性插值。

上采样，指在原始序列中每个离散值之间插入N-1个0，可由矩阵乘法实现。

 ↓↓例如定义一个上采样2（N=2）↓↓

                                   

对上采样(↑N)后的序列进行DTFT，令

上述公式推导出上采样(↑N)可以使得序列频谱在原有的基础上压缩N倍。

下采样，指在原始序列中每隔N-1个值取出一个离散值，可由矩阵乘法实现。

 ↓↓例如定义一个下采样2（N=2）↓↓

 对下采样(↓N)后的序列进行DTFT，令

上述公式推导出下采样(↓N)可以使得序列频谱在原有的基础上扩展N倍。

线性采样类似于上采样，不同的是线性采样插入的值不是0，而是与原序列成线性关系的值。插入后同上采样一样，序列会在原有的基础上进行频谱扩展。可以理解为对声音模拟信号以更高的采样率进行采样。

 

SOLA算法

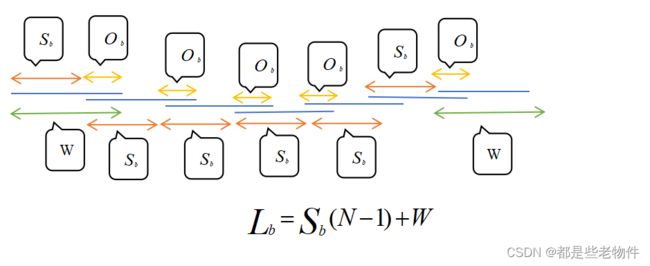
SOLA（Synchronized Overlap-Add）算法可以在不影响声音基频的情况下，对原信号进行变速处理，是OLA算法的改进。OLA算法对原声音信号分帧重合成时，在帧与帧之间的重叠区域只是简单的加权叠加，并未考虑帧与帧之间切入点的连续性与重叠区域的相关性。对于这类缺陷SOLA算法给出了解决方案，它为帧与帧之间的切入点提供了一个位移矢量K，允许切入点在以其为中心的区间[KMin,KMax]内进行移动，且每移动一个单位，两帧之间新产生的重叠区内的数据进行一次相关系数的计算，最后取相关系数最大的那个点作为两帧之间的切入点。SOLA全过程如下↓

• 对原信号进行分解（直接从原序列原点处开始截取W个数作为第一帧序列，接下来每隔个单位进行截取，被截取下的序列（帧）长为W，帧数为N），实际上就是一种交叠分段，相对于连续分段来说，交叠分段能更好地保证分解帧的延续性。其中帧间距为，帧长为W，帧数为N，重叠区=W-,为原信号总长。

 

 

•  将N个分解帧以帧间距 重新合成一个新的序列，新重叠区为=

 

 

 

合成第m帧信号时，如果m=1，那么直接把原信号第一帧序列放入规整序列栏中作为起始帧。对于m>1的分解帧，在应该插入的位置即×m处的左右附近范围[KMin,KMax]内重新找一个插入位置点插入第m帧，这个插入点要满足使要插入的第m帧信号与已合成的信号在重叠区的互相关系数达到最大，互相关系数的计算公式如下，

 

从这互相关系数的计算公式来看，合成分解帧时所用的帧间距并不等于，这是因为偏移量k的存在，通过计算得出的互相关系数最大切入点并不一定会是×m点。也就是说合成分解帧后，规整信号的语速变化并不会严格遵守理论计算的比例。为了解决这个问题，可以把这个位移矢量k放在原信号分解帧序列x[•]中。此时互相关系数计算公式如下，

 

 源码分析

 

Fs=22050;%对模拟声音信号的采样频率
sounds=audiorecorder(Fs,16,2);%sounds保存了声音采样对象.
%16为BitsPerSample（即每个样本值是用几位的二进制数表示).
%一般采样频率提高了，BitsPerSample也要提高。
%因为采样频率提高了，说明对模拟信号的采样间隔减小了，
%采样值被更加细分，采样精度提高。为了匹配采样精度，
%BitsPerSample就需要提高。2表示双声道采样，即有两种
%相同的采样方式在同时进行，最后得出的采样序列是两份。

recordblocking(sounds,3);%开始采样，采样时长为3秒
MyRecording=getaudiodata(sounds);
audiowrite('words.wav',MyRecording,Fs);

figure

[y,Fs]=audioread('words.wav');%以采样频率f=Fs（为被读取文件的采样频率，
%因为要匹配被读取文件采样个数)
%对音频信号文件“words.wav”进行采样，即每隔1/Fs时长在“words.wav”文件上取一个值,
%y以矩阵的形式返回采样信号(随时间变化的声音响度信号，进行了归一化处理)
%y为T*Fs行2列的矩阵(T为"words.wav"音频文件的时长),默认采用双声道采样，即同时采样两份并分为两列

t=(0:length(y)-1)/Fs;%变换出时间尺寸坐标。length(y)相当于max(size(y)),
%即在y矩阵的行数和列数中取最大的那个数
%size(y)返回y矩阵的行数和列数

plot(t,y);
title('声音信号在时间轴上的双声道强度分布');

figure

averageY=0.5*(y(:,1)+y(:,2));%对双声道采样得来的两份采样本进行平均，减小采样误差，
% y(:,1)表示取y矩阵第一列的所有数，冒号:代表所有

N=(0:length(y)-1);%得到采样点数
interval=(0:0.5:length(y)-1);%需要进行插值的横坐标值

ProcessedSound=interp1(N,averageY',interval,'linear');
%得到对averageY'(以N为横坐标)向量插值后的的向量ProcessedSound(以interval为横坐标)

plot(interval,ProcessedSound);
title('对声音进行插值处理后在时间轴上的模拟采样分布');

 

function [ NewSign ] = SOLAadjustment( specification )
%读取一段音频并进行SOLA算法处理，根据specification的数值大小输出相应的变调不变速的声音

[Y,Fs] = audioread('words.wav');
b=specification;  %b=Sb/Sa,原信号帧间距Sb与规整后信号帧间距Sa的比值，是规整因子的倒数
OriginalSign=Y(:,1)'; %在双声道采样数据向量Y中，取第一列所有元素      
u=b*1000;
ResampleSign=resample(OriginalSign,u,1000);
%以u/1000=b倍原采样率的新采样率对OriginalSign按照一定运算法则进行重采样，
%得到的ResampleSign序列长度是OriginalSign的u/1000=b倍
%b<1,时域压缩而频域扩展，声音表现为高频，同时由于序列长度变短，语速变快；
%b>1,时域扩展而频域压缩，声音表现为低频，同时由于序列长度变长，语速变慢。
%ResampleSign虽然音调改变了但语速也改变了，所以需要用SOLA算法对ResampleSign进行处理(规整时长),
%从而得到一个语速和原始信号OriginalSign一样的规整信号 NewSign

S=400;   %信号序列一帧的长度，分解信号(ResampleSign)与规整后信号的帧长是一样的

Overlap=200; %规整后的输出信号的数据重叠区长度

Pmax=170; %允许寻找相关性最大移动位数，作用在原始信号帧序列中。如此做的原因已经介绍过。

B=S-Overlap; %规整后的输出序列间距

OriginalLen= length(OriginalSign);  %经过重采样得到的ResampleSign序列虽然音调改变了，
%但是它的语速也相应的变慢了或变快了，
%所以为了实现语速不变，规整后的输出序列NewSign的长度应该要和OriginalLen序列相等

NewSign= zeros(1, OriginalLen);  %为规整后的输出序列开辟长度，且与OriginalLen序列长度相等

ratio = (1:Overlap)/(Overlap+1); %找到相关最大的切入点后，重叠区的加权叠加系数
i = 1:Overlap;          
app=1:B;      %信号追加移动变量

CalSeries = [ResampleSign, zeros(1,400)]; %以重采样信号为模板新建序列用以计算

NewSign(1:S) = ResampleSign(1:S); %取重采样信号第一帧给（将要规整的）新信号            
for newpos = B:B:(OriginalLen-S)    
        Originalpos = round(b * newpos);              
        y = NewSign(newpos + i);           
        rxy = zeros(1, Pmax+1);         
        rxx = zeros(1, Pmax+1);         
        Pmin=0;  
        %相关性计算
        for p =Pmin:Pmax        
            x = CalSeries(Originalpos + p + i);
            rxx(p+1) = norm(x);             
            rxy(p+1) = (y*x');          
        end
        Rxy = (rxx ~= 0).*rxy./(rxx+(rxx==0));    
        pm = min(find(Rxy == max(Rxy))-1);       
        bestpos = Originalpos+pm;        %当前最佳匹配位置，相关最大切入点  
        NewSign(newpos+i)=((1-ratio).*NewSign(newpos+i))+(ratio.*CalSeries(bestpos+i));  
        %重叠区的加权叠加

        NewSign(newpos+Overlap+app) = CalSeries(bestpos+Overlap+app); 
         %去除重叠部分信号追加在新信号输出序列  
end

end

原理分析

 对一段模拟信号采样得来的数据先进行一次插值处理(即可在每个样本点之间再插入一个或多个值，这些新插入的值并不是无规则的，而是根据源数据的分布走向，按照某种函数关系产生的值。),插值后会发现样本数据的DFT幅频图上产生了频率压缩现象，即低频部分明显增强而高频部分明显减少。事实上插值这个操作使得采样数据在时域上进行了扩展(因为在原先的采样数据之间被新插入了值，这个现象可以抽象成时域扩展)，故插值后的DFT在频谱上会产生压缩。此时若还是以原先的采样率Fs播放插值后的采样数据，声音将表现为慢速浑厚的大叔音。之后以该采样序列作为扬声器的输入信号，我们只要通过增大采样率来减小每一个采样数据的播放时间就能得到音频较高的萝莉音。之所以将采样得来的数据先进行插值处理是为了提高声音采样数据的丰富度，这样可以有效地减小声音变换后的失真程度(比如某些该有的音没有发出来)。

 

对于一段音频信号，假设计算机里的扬声器原来的播放每一个信号值的时间间隔为1/Fs，当将时间间隔改为1/0.7Fs时，声音信号相当于在时域中关于时间轴进行了扩展，在频域上关于频率轴进行了压缩，压缩后的频谱中低频部分明显增加，从而产生了低频的浑厚声音。同时，由于播放每一个声音值的时间间隔延长，声音的语速变慢，声音播放时长变长。对于萝莉音同理分析。

 

另外若将一段声音信号乘以一个正弦或余弦信号，根据信号的调制可以分析得，声音频谱将向左向右分别移动正余弦频率值的长度，移动后的频谱在高频上的泛音明显增多，从而使得声音更加尖锐。但如果移动长度过大，将导致低频部分缺失，产生声音失真。

 

总结

声音的根本在于其频谱的分布，透过其外在表现去分析其内在的组成成分，将会很清晰地观察到声音的各频率的分布，通过一定信号处理手段改变其频谱结构，从而达到我们想要的声音效果。