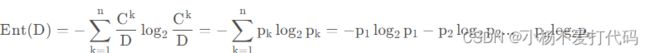机器学习7

目录

朴素贝叶斯算法   sklearn.naive_bayes.MultinomialNB(alpha = 1.0)

 定义：

贝叶斯公式

应用场景

拉普拉斯平滑系数

朴素贝叶斯算法对新闻进行评估

 优点

缺点

决策树     DecisionTreeClassifier

概念

决策树分类的原理

决策树可视化    export_graphviz

优点

缺点

随机森林    DecisionTreeRegressor

概念

 ​编辑

 代码实现

---

朴素贝叶斯算法   sklearn.naive_bayes.MultinomialNB(alpha = 1.0)

 定义：

假定特征与特征之间是相互独立的，然后使用贝叶斯公式求概率

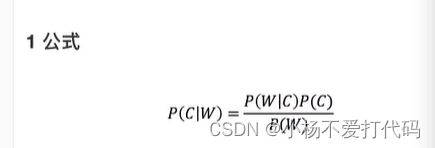
贝叶斯公式

应用场景

进行文本分类，使用单词作为特征

拉普拉斯平滑系数

P(F1​∣C)=N+αm/Ni​+α（默认情况下a=1）,拉普拉斯系数就是给分子加上数，避免概率为0的情况

​1.α即拉普拉斯平滑系数，通常为1。

2.m是训练集文档中统计出的特征词个数。在上面例子里，训练集中有4篇文章，共有6种词，所以m=6。

朴素贝叶斯算法对新闻进行评估

用朴素贝叶斯算法对新闻进行评估

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
#获取数据
news=fetch_20newsgroups(subset="all")

#划分数据集
x_train,x_test,y_train,y_test=train_test_split(news.data,news.target)

#特征工程
transfer=TfidfVectorizer()
x_train=transfer.fit_transform(x_train)
x_test=transfer.transform(x_test)

#朴素贝叶斯算法预估流程
estimator=MultinomialNB()
estimator.fit(x_train,y_train)

#模型评估
y_predict=estimator.predict(x_test)
print("y_test:",y_test)
print("y_predict:",y_predict)
print("直接比对真实值和预测值：\n",y_test==y_predict)
accuracy=estimator.score(x_test,y_test)
print("准确率：\n",accuracy)

 优点

1.朴素⻉叶斯模型发源于古典数学理论，有稳定的分类效率

2.对缺失数据不太敏感，算法也⽐较简单，常⽤于⽂本分类

3.分类准确度⾼，速度快

缺点

1.由于使⽤了样本属性独⽴性的假设，所以如果特征属性关联性比较强时效果就不太好

2.需要计算先验概率，⽽先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳

决策树     DecisionTreeClassifier

    概念

是⼀种树形结构；本质是⼀颗由多个判断节点组成的树其中每个内部节点表示⼀个属性上的判断；每个分⽀代表⼀个判断结果的；输出最后每个叶节点代表⼀种分类结果

决策树分类的原理

1.信息熵：度量样本集合纯度最常用的一项指标。从信息完整性角度来说，当系统的有序状态一致时，数据越集中的地方，熵值越小，数据越分散的地方，熵值越大。

计算公式：

2.信息增益：以某个特征划分数据集前后熵的差值。

由于熵可以表示样本集合的不确定性，熵越大，样本的不确定性就越大。因此，我们可以通过计算以某个特征划分了数据集之前的熵和之后的熵的差值，来判断这个特征划分数据集的效果。

3.信息增益率（评判标准）：增益率是⽤前⾯的信息增益和特征a对应的“固有值”(intrinsic value) 的⽐值来共同定义的。

4.代码实现：

#如何高效的进行决策，思想的来源⾮常朴素，程序设计中的if-else结构就是早期决策树用来分割数据的⼀种分类学习⽅法
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier

iris=load_iris()
#划分数据集
x_train,x_test,y_train,y_test=train_test_split(iris.data,iris.target,random_state=6)
#决策树预估器
estimator=DecisionTreeClassifier(criterion="entropy")
estimator.fit(x_train,y_train) #调用完毕，模型生成
#模型评估
y_predict=estimator.predict(x_test)
print("y_predict:",y_predict)
print("直接比对真实值和预测值：\n",y_test==y_predict)
accuracy=estimator.score(x_test,y_test)
print("准确率：",accuracy)

决策树可视化    export_graphviz

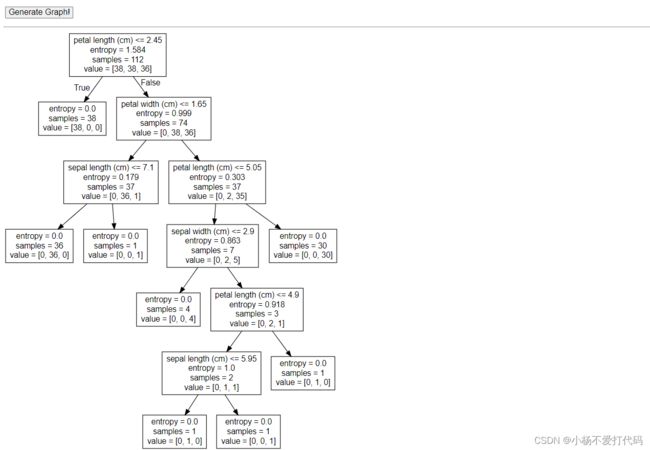
#决策树可视化
export_graphviz(estimator,out_file='iris',feature_names=iris.feature_names)

 

优点

简单的理解和解释，数目可视化

缺点

可以创建不能很好地推广数据过于复杂的数，也称为过拟合

改进：随机森林

随机森林    DecisionTreeRegressor

概念

包含多个决策树的分类器

 

 代码实现

import numpy as np
from sklearn.tree import DecisionTreeRegressor

class rfr:

    def __init__(self, n_estimators = 100, random_state = 0):
        # 随机森林的大小
        self.n_estimators = n_estimators
        # 随机森林的随机种子
        self.random_state = random_state

    def fit(self, X, y):
        """
        随机森林回归器拟合
        """
        # 决策树数组
        dts = []
        n = X.shape[0]
        rs = np.random.RandomState(self.random_state)
        for i in range(self.n_estimators):
            # 创建决策树回归器
            dt = DecisionTreeRegressor(random_state=rs.randint(np.iinfo(np.int32).max), max_features = "auto")
            # 根据随机生成的权重，拟合数据集
            dt.fit(X, y, sample_weight=np.bincount(rs.randint(0, n, n), minlength = n))
            dts.append(dt)
        self.trees = dts

    def predict(self, X):
        """
        随机森林回归器预测
        """
        # 预测结果
        ys = np.zeros(X.shape[0])
        for i in range(self.n_estimators):
            # 决策树回归器
            dt = self.trees[i]
            # 依次预测结果
            ys += dt.predict(X)
        # 预测结果取平均
        ys /= self.n_estimators
        return ys