【计算智能】读书笔记 第八章节 分布估计算法
文章目录
- 1. 分布估计算法简介
-
- 与遗传算法的对比
- 2. 算法流程介绍
-
- 2.1 算法原理
- 2.2 算法变体
-
- 2.2.1 EDA算法变体UMDA
- 2.2.2 EDA算法变体PBIL
- 2.3 算法流程
- 3. 计算例子
- 4. 算法的改进以及理论研究
-
- 4.1 链式概率模型
- 4.2 树状概率模型
-
- 4.3 贝叶斯网络概率模型
- 4.4 高斯概率模型
- 5. 混合分布估计算法
-
- 5.1 分布估计算法与遗传算法结合
- 5.2 分布估计算法与差分进化算法结合
- 6. 并行分布估计算法
-
- 6.1 种群级别并行化
- 6.2 适应评估并行化
- 写在最后
1. 分布估计算法简介
分布估计算法, 又称为基于概率模型的遗传算法,是20世纪90年代初提出的一种新型的启发式算法,其思想起源于遗传算法,但却有着与遗传算法不同的进化模式,结合了统计学习理论和遗传算法的实现原理,通过构建概率模型、采样和更新概率模型等操作实现群体的进化。
与遗传算法的对比
分布估计算法提出了一种新的进化模式,在分布估计算法张,没有传统的交叉、变异等遗传算法的操作,取而代之的是概率模型的学习和采样,分布估计算法通过一个概率模型描述候选解在空间中的分布,采用统计学习手段,从群体的宏观特征建立一个描述解分布的概率模型,然后对该概率模型随机采样获得新的种群,从而实现种群的迭代进化。下图是分布估计算法与遗传算法的对比:
2. 算法流程介绍
2.1 算法原理
通过一个概率模型描述候选解在空间中的分布,再用统计学习的手段,从群体宏观的角度建立一个描述解分布的 概率模型,然后对概率模型产生新的种群,接着反复进行
2.2 算法变体
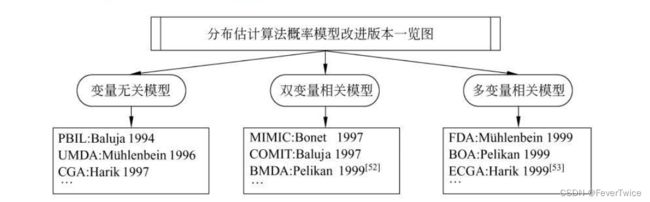
EDA有很多不同的变体,包括下面的一些:
- 变量无关:PBIL、UMDA、gCA
- 双变量相关:MIMIC、BMDA
- 多变量相关:EGCA、FDA、BOA
- 混合分布式:EDA+粒子群、EDA+遗传算法、EDA+差分进化算法
- 并行分布式估计算法:主从模式、岛屿模式
2.2.1 EDA算法变体UMDA
由德国学者 Muhlenbein 在 1996 年提出,算法描述:
- 随机产生 M M M 个个体作为初始种群;
- 然后计算 M M M 个个体的适应值,如果符合终止条件,算法结束,否则继续进行;
- 选择最优的 N N N 个个体用来更新概率向量 p ( x ) , N < = M p(x), N<=M p(x),N<=M 。更新过程如下:
p l ( x ) = p ( x ∣ D l S ) = 1 N ∑ k = 1 N s l k p_l(x)=p\left(x \mid D_l^S\right)=\frac{1}{N} \sum_{k=1}^N s_l^k pl(x)=p(x∣DlS)=N1k=1∑Nslk - 由新的概率模型采样 M M M 次,得到新一代群体,返回第 2 步。
2.2.2 EDA算法变体PBIL
由美国卡耐基梅隆大学的 Baluja 在 1994 年提出,算法描述:
- 随机产生 M M M 个个体作为初始种群;
- 然后计算 M M M 个个体的适应值,如果符合终止条件,算法结束,否则继续进行;
- 选择最优的 N N N 个个体用来更新概率向量 p ( x ) , N < = M \mathrm{p}(\mathrm{x}), \mathrm{N}<=\mathrm{M} p(x),N<=M 。更新过程如下:
p l + 1 ( x ) = ( 1 − α ) p l ( x ) + α 1 N ∑ k = 1 N s l k p_{l+1}(x)=(1-\alpha) p_l(x)+\alpha \frac{1}{N} \sum_{k=1}^N s_l^k pl+1(x)=(1−α)pl(x)+αN1k=1∑Nslk - 由新的概率模型采样 M M M 次,得到新一代群体,返回第 2 步。
2.3 算法流程
通用算法流程为:
- 随机生成M个个体作为初始种群
- 对第L代种群计算个体适应度,判断是否满足终止条件,满足停止循环,否则继续
- 根据适应度数值选前N个(N<=M)优势个体,组成第L+1代优势子种群
- 对概率模型进行随机采样,生成新种群(规模M),返回第二步
3. 计算例子
使用分布估计算法求解 0-1 背包问题,计算步骤如下:
- Step 1: 以概率 T = ( p 1 , p 2 , … , p n ) T = ( 0.5 , 0.5 , … , 0.5 ) T T=\left(p_1, p_2, \ldots, p_n\right)^T=(0.5,0.5, \ldots, 0.5)^T T=(p1,p2,…,pn)T=(0.5,0.5,…,0.5)T 随机产生 N N N 个个体组成一个初始种群;
- Step 2: 评估初始种群中所有个体的适应度,保留最好解;
- Step 3: 按适应度从高到低的顺序对种群进行排序,并从中选出最优的 m m m 个个体 ( m ≤ N ) (m \leq N) (m≤N);
- Step 4: 分析产生的 m m m 个个体所包含的信息, 估计每个变量取 1 的 ( p 1 , p 2 , … , p n ) T \left(p_1, p_2, \ldots, p_n\right)^T (p1,p2,…,pn)T;
- Step 5: 从构建的概率模型 ( p 1 , p 2 , … , p n ) T \left(p_1, p_2, \ldots, p_n\right)^T (p1,p2,…,pn)T 中采样,得到 N N N 个新样本,构成新种群;
- Step 6: 若达到算法的终止条件则结束(如达到规定迭代次数 n max n_{\text {max }} nmax ), 否则执行 Step 2。该分布估计算法的时间复杂性估算如下: 以计算适应度操作花费最多,所以,时间复杂性大约为 O ( N ⋅ n max ) O\left(N \cdot n_{\text {max }}\right) O(N⋅nmax ) 。
4. 算法的改进以及理论研究
4.1 链式概率模型
最早的变量相关分布估计算法是 Bonet 1997 年提出的 基于最大互信息的分布估计算法 (Mutual Information Maximization for Input Clustering, C)
第一步: 计算所有 h ^ ( X j ) \hat{h}\left(X_j\right) h^(Xj), 将值最小的变量标号为 i n i_n in, 即 i n = arg min j h ^ ( X j ) i_n=\arg \min _j \hat{h}\left(X_j\right) in=argminjh^(Xj); 令 k = n − 1 k=n-1 k=n−1 。
第8章 分布估计算法 163
第二步:对所有 j ( j ≠ i k + 1 ⋯ i n ) j\left(j \neq i_{k+1} \cdots i_n\right) j(j=ik+1⋯in) 计算 h ^ ( X j ∣ X i k + 1 ) \hat{h}\left(X_j \mid X_{i_{k+1}}\right) h^(Xj∣Xik+1) 并将值最小的变量标号为 i k i_k ik, 即 i k = arg min j h ^ ( X j ∣ X i k + 1 ) , j ≠ i k + 1 ⋯ i n ; i_k=\arg \min _j \hat{h}\left(X_j \mid X_{i_{k+1}}\right), \quad j \neq i_{k+1} \cdots i_n ; \quad ik=argminjh^(Xj∣Xik+1),j=ik+1⋯in; 令 k = k − 1 k=k-1 k=k−1
第三步: 若 k = 0 k=0 k=0 则结束, 否则执行第二步。
当概率分布被确定好后, MIMIC 按如下流程从链尼到链首依次产生一个新样本
第一步:根据概率密度函数 p ^ ( X i n ) \hat{p}\left(X_{i_n}\right) p^(Xin), 产生 X i n X_{i_n} Xin
第二步: 对所有的 k = n − 1 , n − 2 , ⋯ , 2 , 1 k=n-1, n-2, \cdots, 2,1 k=n−1,n−2,⋯,2,1, 根据 p ^ ( X i k ∣ X i k + 1 ) \hat{p}\left(X_{i_k} \mid X_{i_{k+1}}\right) p^(Xik∣Xik+1) 产生 X i k X_{i_k} Xik
4.2 树状概率模型
COMIT(Combining Optimizers with Mutual Information Trees)是Baluja在1997年提出的另一种变量相关分布估计算法 COMIT和MIMIC 都是解决双变相关的分布估计算法,但与 MIMIC 不同的是COMIT采用一种树状结构来描述变之间的关系。其结构关系如下所示:
4.3 贝叶斯网络概率模型
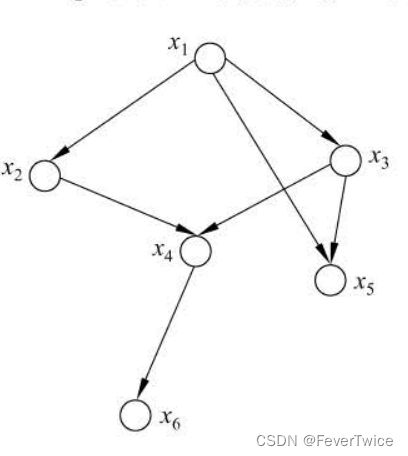
贝叶斯网络是描述变量之间概率依赖关系的数学模型, 其拓扑结构是一个有向无环图 (DAG), 如下图所示, 其中每个节点代表一个变量, 而每条边则表示变量之间的概率依赖关系。
4.4 高斯概率模型
高斯分布又称为正态分布, 通常记为 N ( μ , σ 2 ) N\left(\mu, \sigma^2\right) N(μ,σ2), 其中 μ \mu μ 为分布的均值, σ \sigma σ 为分布的方差, 其函数图像如下图所示。高斯概率模型是实数编码分布估计算法的经典概率模型。 PBIL 和 UMDA 对应的实数编码分布估计算法 PBILc 和 UMDAc 所采用的概率模型都 是高斯概率模型 。此外, 多元高斯模型也是解决多变量相关的实数编码分布估计算 法常采用的概率模型。
5. 混合分布估计算法
5.1 分布估计算法与遗传算法结合
分布估计算法与遗传算法都是基于种群的进化算法,它们的不同之处在生成种群的机制不同。为了验证哪 种算法的性能更优, Larraga 和 Lozano等学者曾设计了多种问题来进行测试。

在GA-EDA 中,新的种群由 GA EDA 共同生成 具体地说, GA和EDA 是在同种群的基础 按照各自的机制分别产 子种群,然后再将这两个子种群组合成新的种群,如此完成迭代的进化过程。
5.2 分布估计算法与差分进化算法结合
差分进化算法 (differential Evolution), 也是一种基于种群的 机搜索算法, 它利用当前种群之间的差异信息来引导搜索。 随着 进化代数的增加,个体之间的差异性将越来越小,而简单的差分进化算法缺乏有效的机制利用和产生搜索空间中的全局的信息,因而常常会收敛于局部最优解。
6. 并行分布估计算法
6.1 种群级别并行化
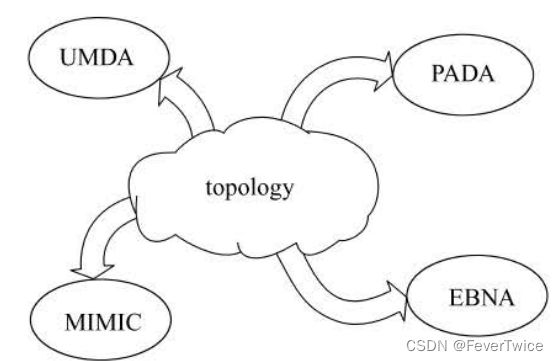
简单地说,该类 法通常将种群分成多个子种群,每个子种群在不同的机器上运行,然后各个子种群通过迁移等机制进行通信,达到综合信息的目的。
下图就是dEDA 中每个岛屿运行不同的示意图
6.2 适应评估并行化
适应度评估通常是算法中最耗时的部分,而采用多台机器并行计算种群中的适应度是提高进化算法搜索速度最直接有效的方法之 一。
写在最后
各位看官,都看到这里了,麻烦动动手指头给博主来个点赞8,您的支持作者最大的创作动力哟!
才疏学浅,若有纰漏,恳请斧正
本文章仅用于各位作为学习交流之用,不作任何商业用途,若涉及版权问题请速与作者联系,望悉知