Word2Vec(Skip-Gram和CBOW) - PyTorch

---

• 词向量是用于表示单词意义的向量，也可以看作是词的特征向量。将词映射到实向量的技术称为词嵌入。

一、词嵌入(Word2vec)

独热向量不能准确表达不同词之间的相似度，word2vec的提出就是为了解决这个问题，它将每个词映射到一个固定⻓度的向量，这些向量能更好地表达不同词之间的相似性和类比关系。word2vec包含两个模型：Skip-Gram和CBOW，它们的训练依赖于条件概率。由于是不带标签的数据，因此Skip-Gram和CBOW都是自监督模型。

1.Skip-Gram

Skip-Gram：中心词预测周围词

每个词都有两个$d$维的向量表示，用于计算条件概率。对于词典中索引为$i$的任何词，分别用${\mathbf{v}}_i\in {\mathbb{R}}^d$和${\mathbf{u}}_i\in {\mathbb{R}}^d$表示其用作中心词和上下文词时的两个向量。给定中心词$w_c$（下标表示在词典中的索引），生成任何上下文词$w_o$的条件概率可以通过对向量点积的softmax操作来建模：
$$P(w_o\mid w_c)=\frac{\text{exp}({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)}{{\sum }_{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}\text{\hspace{1em}(1)}$$
其中，词表索引集$\mathcal{V}=\{0,1,\dots ,|\mathcal{V}|-1\}$。

给定长度为$T$的文本序列，其中时间步$t$处的词表示为$w^{(t)}$。假设上下文词是在给定任何中心词的情况下独立生成的。对于上下文窗口$m$，Skip-Gram的似然函数是在给定任何中心词的情况下生成所有上下文词的概率：
$$\prod _{t=1}^T\prod _{-m\le j\le m,j\ne 0}P(w^{(t+j)}\mid w^{(t)})\text{\hspace{1em}(2)}$$

2.CBOW模型

CBOW：周围词预测中心词

由于CBOW中存在多个上下文词，因此在计算条件概率时对这些上下文词向量进行平均。对于字典中索引$i$的任意词，分别用${\mathbf{v}}_i\in {\mathbb{R}}^d$和${\mathbf{u}}_i\in {\mathbb{R}}^d$表示用作上下文词和中心词的两个向量（符号与Skip-Gram中相反）。给定上下文词$w_{o_1},\dots ,w_{o_{2m}}$（在词表中索引是$o_1,\dots ,o_{2m}$）生成任意中心词$w_c$的条件概率为:

$$P(w_c\mid w_{o_1},\dots ,w_{o_{2m}})=\frac{\text{exp}\left(\frac{1}{2m}{\mathbf{u}}_c^{\top }({\mathbf{v}}_{o_1}+\dots ,+{\mathbf{v}}_{o_{2m}})\right)}{{\sum }_{i\in \mathcal{V}}\text{exp}\left(\frac{1}{2m}{\mathbf{u}}_i^{\top }({\mathbf{v}}_{o_1}+\dots ,+{\mathbf{v}}_{o_{2m}})\right)}\text{\hspace{1em}(3)}$$
给定长度为$T$的文本序列，其中时间步$t$处的词表示为$w^{(t)}$。对于上下文窗口$m$，CBOW的似然函数是在给定其上下文词的情况下生成所有中心词的概率：

$$\prod _{t=1}^{T}P(w^{(t)}\mid w^{(t-m)},\dots ,w^{(t-1)},w^{(t+1)},\dots ,w^{(t+m)})\text{\hspace{1em}(4)}$$

二、负采样和分层softmax

Skip-Gram的主要思想是使用softmax运算来计算基于给定的中心词$w_c$生成上下文字$w_o$的条件概率。由于softmax操作的性质，上下文词可以是词表$\mathcal{V}$中的任意项，包含与整个词表大小一样多的项的求和。因此， Skip-Gram的梯度计算和CBOW的梯度计算都包含求和。但通常一个词典有几十万或数百万个单词，求和的梯度的计算成本是巨大的！

为了降低计算复杂度，下面以Skip-Gram为例学习两种近似计算方法：负采样和分层softmax。

1.负采样

给定中心词$w_c$的上下文窗口，任意上下文词$w_o$来自该上下文窗口的被认为是由下式建模概率的事件：

$$\begin{gathered} P(D=1\mid w_c,w_o)=\sigma ({\mathbf{u}}_o^{\top }{\mathbf{v}}_c) \\ =\frac{\exp ({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)}{1+\exp ({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)} \\ =\frac{1}{1+\exp (-{\mathbf{u}}_o^{\top }{\mathbf{v}}_c)}\text{\hspace{1em}(5)} \end{gathered}$$
负采样之前用的是softmax(多分类)，现在是sigmoid(二分类)。

二分类，多分类可以看之前的逻辑回归和多项逻辑回归这篇博客，实战可以看逻辑回归实战-股票客户流失预警模型(Python代码)这个。

最大化联合概率，给定长度为$T$的文本序列，以$w^{(t)}$表示时间步$t$的词，上下文窗口为$m$，公式为：

$$\prod _{t=1}^T\prod _{-m\le j\le m,j\ne 0}P(D=1\mid w^{(t)},w^{(t+j)})\text{\hspace{1em}(6)}$$
然而，公式6只考虑那些正样本的事件。仅当所有词向量都等于无穷大时，联合概率才最大化为1。当然，这样的结果毫无意义。为了使目标函数更有意义，负采样添加从预定义分布中采样的负样本。

用$S$表示上下文词$w_o$来自中心词$w_c$的上下文窗口的事件。对于这个涉及$w_o$的事件，从预定义分布$P(w)$中采样$K$个不是来自这个上下文窗口噪声词。用$N_k$表示噪声词$w_k$（$k=1,\dots ,K$）不是来自$w_c$的上下文窗口的事件。假设正例和负例$S,N_1,\dots ,N_K$的这些事件是相互独立的。负采样将原来Skip-Gram的联合概率（公式2）重写，改变条件概率为下式：
$$\begin{gathered} P(w^{(t+j)}\mid w^{(t)})\approx \\ P(D=1\mid w^{(t)},w^{(t+j)})\prod _{k=1,w_k\sim P(w)}^{K}P(D=0\mid w^{(t)},w_k) \end{gathered}$$
损失函数是负对数似然，现在梯度的计算成本就不再和词表大小有关，而是和负采样中噪声词的个数$K$(是个超参数，$K$越小计算成本越低)有关。

2.分层Softmax

分层Softmax使用二叉树，其中树的每个叶节点表示词表$\mathcal{V}$中的一个词。

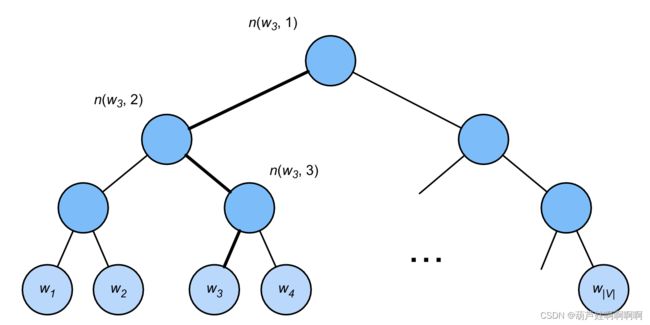
用$L(w)$表示二叉树中表示字$w$从根节点到叶节点的路径上的节点数（包括两端）。设$n(w,j)$为该路径上的$j^{\mathrm{t}\mathrm{h}}$节点，其上下文字向量为${\mathbf{u}}_{n(w,j)}$。

例如，$L(w_3)=4$。分层softmax将条件概率近似为
$$P(w_o\mid w_c)\approx \prod _{j=1}^{L(w_o)-1}\sigma \left([[n(w_o,j+1)=\text{leftChild}(n(w_o,j))]]\cdot {\mathbf{u}}_{n(w_o,j)}^{\top }{\mathbf{v}}_c\right)$$
其中，$\text{leftChild}(n)$是节点$n$的左子节点：如果$x$为真，$[[x]]=1$；否则$[[x]]=-1$。

以计算上图中给定词$w_c$生成词$w_3$的条件概率为例。这需要$w_c$的词向量${\mathbf{v}}_c$和从根到$w_3$的路径（图中加粗的路径）上的非叶节点向量之间的点积，该路径依次向左、向右和向左遍历：

$$P(w_3\mid w_c)=\sigma ({\mathbf{u}}_{n(w_3,1)}^{\top }{\mathbf{v}}_c)\cdot \sigma (-{\mathbf{u}}_{n(w_3,2)}^{\top }{\mathbf{v}}_c)\cdot \sigma ({\mathbf{u}}_{n(w_3,3)}^{\top }{\mathbf{v}}_c)$$
由$\sigma (x)+\sigma (-x)=1$，它认为基于任意词$w_c$生成词表$\mathcal{V}$中所有词的条件概率总和为1：${\sum }_{w\in \mathcal{V}}P(w\mid w_c)=1.$

在二叉树结构中，$L(w_o)-1$大约与$\mathcal{O}({\text{log}}_2|\mathcal{V}|)$是一个数量级。当词表大小$\mathcal{V}$很大时，与没有近似训练的相比，使用分层softmax的每个训练步的计算代价显著降低。

小结

• 负采样通过考虑相互独立的事件来构造损失函数，这些事件同时涉及正例和负例。训练的计算量与每一步的噪声词数成线性关系。
• 分层softmax使用二叉树中从根节点到叶节点的路径构造损失函数。训练的计算成本取决于词表大小的对数。

三、用于预训练词嵌入的数据集

这里使用的数据集是Penn Tree Bank(PTB)。该语料库取自“华尔街日报”的文章，分为训练集、 验证集和测试集。在原始格式中，文本文件的每一行表示由空格分隔的一句话。在这里，我们将每个单词视为一个词元。

import math
import os
import random
import torch
from torch import nn
from d2l import torch as d2l
from torch.nn import functional as F

d2l.DATA_HUB['ptb'] = (d2l.DATA_URL + 'ptb.zip',
                       '319d85e578af0cdc590547f26231e4e31cdf1e42')


def read_ptb():
    """将PTB数据集加载到文本行的列表中"""
    data_dir = d2l.download_extract('ptb')
    # Read the training set.
    with open(os.path.join(data_dir, 'ptb.train.txt')) as f:
        raw_text = f.read()
    return [line.split() for line in raw_text.split('\n')]

• 构建词表，出现次数少于10次的单词将由“”词元替换。

sentences = read_ptb() # sentences数: 42069
vocab = d2l.Vocab(sentences, min_freq=10) # vocab size: 6719

1.下采样

文本数据通常有“the”、“a”和“in”等高频词，这些词提供的有用信息很少。此外，大量（高频）单词会使训练速度很慢。因此，当训练词嵌入模型时，可以对高频单词进行下采样。即数据集中的每个词$w_i$将有概率地被丢弃

$$P(w_i)=\max \left(1-\sqrt{\frac{t}{f(w_i)}},0\right)$$
其中，$P(w_i)$指被丢弃的概率，$f(w_i)$指单词$w_i$在数据集中出现的频率，常量$t$是超参数（下面代码中设置为$10^{-4}$）。只有当$f(w_i)>t$时，（高频）词$w_i$才能被丢弃，$f(w_i)$越高，被丢弃的概率越高。

• 下采样高频词

def subsample(sentences, vocab):
    """下采样高频词"""
    # 排除未知词元''
    sentences = [[token for token in line if vocab[token] != vocab.unk]
                 for line in sentences]
    counter = d2l.count_corpus(sentences)
    num_tokens = sum(counter.values())

    # 如果在下采样期间保留词元，则返回True
    # counter[token]:token的频数；num_tokens：总的token数量(不包含)
    def keep(token):
        return(random.uniform(0, 1) <
               math.sqrt(1e-4 / counter[token] * num_tokens))
    
    return ([[token for token in line if keep(token)] for line in sentences],
            counter)

subsampled, counter = subsample(sentences, vocab)

• 下采样后，高频词的采样数会显著减少，而低频词的采样数不会改变，全部保留

def compare_counts(token):
    return (f'"{token}"的数量：'
            f'之前={sum([l.count(token) for l in sentences])}, '
            f'之后={sum([l.count(token) for l in subsampled])}')
'''
def compare_counts(token):
    return (f'"{token}"的数量：'
            f'之前={counter[token]},'
            f'之后={d2l.count_corpus(subsampled)[token]}')
'''
print(compare_counts('in'))
print(compare_counts('join'))
# "in"的数量：之前=18000, 之后=1191
# "join"的数量：之前=45, 之后=45

2.中心词和上下文词的提取

上下文窗口大小是1到max_window_size的随机值

def get_centers_and_contexts(corpus, max_window_size):
    """返回Skip-Gram的中心词和上下文词"""
    centers, contexts = [], []
    for line in corpus:
        # 要形成“中心词-上下文词”对，每个句子至少需要有2个词
        if len(line) < 2:
            continue
        centers += line
        for i in range(len(line)):  # 上下文窗口中间i
            window_size = random.randint(1, max_window_size)
            indices = list(range(max(0, i - window_size),
                                 min(len(line), i + 1 + window_size)))
            # 从上下文词中排除中心词
            indices.remove(i)
            contexts.append([line[idx] for idx in indices])
    # centers：包含corpus所有词，contexts：所有中心词的上下文
    return centers, contexts

3.负采样

根据预定义的分布对噪声词进行采样，采样分布通过变量sampling_weights传递

class RandomGenerator:
    """根据n个采样权重在{1,...,n}中随机抽取"""
    def __init__(self, sampling_weights):
        # Exclude
        self.population = list(range(1, len(sampling_weights) + 1))
        self.sampling_weights = sampling_weights
        self.candidates = []
        self.i = 0

    def draw(self):
        if self.i == len(self.candidates):
            # 缓存k个随机采样结果
            self.candidates = random.choices(
                self.population, self.sampling_weights, k=10000)
            self.i = 0
        self.i += 1
        return self.candidates[self.i - 1]

对于一对中心词和上下文词，随机抽取$K$个（实验中为5个）噪声词。根据word2vec论文中的建议，将噪声词$w$的采样概率$P(w)$设置为其在字典中的相对频率，其幂为0.75。

def get_negatives(all_contexts, vocab, counter, K):
    """返回负采样中的噪声词"""
    # 索引为1、2、...（索引0是词表中排除的未知标记）
    sampling_weights = [counter[vocab.to_tokens(i)]**0.75
                        for i in range(1, len(vocab))]
    all_negatives, generator = [], RandomGenerator(sampling_weights)
    for contexts in all_contexts:
        negatives = []
        while len(negatives) < len(contexts) * K:
            neg = generator.draw()
            # 噪声词不能是上下文词
            if neg not in contexts:
                negatives.append(neg)
        all_negatives.append(negatives)
    return all_negatives

sentences = read_ptb()
vocab = d2l.Vocab(sentences, min_freq=10)
subsampled, counter = subsample(sentences, vocab)
# 下采样后，将词元映射到它们在语料库中的索引
corpus = [vocab[line] for line in subsampled]
all_centers, all_contexts = get_centers_and_contexts(corpus, 5)
all_negatives = get_negatives(all_contexts, vocab, counter, 5)

4.小批量加载训练实例

在小批量中，$i^{\mathrm{t}\mathrm{h}}$个样本包括中心词及其$n_i$个上下文词和$m_i$个噪声词。由于上下文窗口大小不同，$n_i+m_i$对于不同的$i$是不同的。因此，对于每个样本，我们在contexts_negatives个变量中将其上下文词和噪声词连结起来，并填充零，直到连结长度达到max_len。

掩码变量masks是为了在计算损失时排除填充。为了区分正反例，定义labels变量将上下文词与噪声词分开。其中labels中的1对应于contexts_negatives中的上下文词的正例，0对应负例。

输入data是长度等于批量大小的列表，其中每个元素是由中心词center、其上下文词context和其噪声词negative组成的样本。

def batchify(data):
    """返回带有负采样的Skip-Gram的小批量样本"""
    max_len = max(len(c) + len(n) for _, c, n in data)
    centers, contexts_negatives, masks, labels = [], [], [], []
    for center, context, negative in data:
        cur_len = len(context) + len(negative)
        centers += [center]
        contexts_negatives += \
            [context + negative + [0] * (max_len - cur_len)]
        masks += [[1] * cur_len + [0] * (max_len - cur_len)]
        labels += [[1] * len(context) + [0] * (max_len - len(context))]
    return (torch.tensor(centers).reshape((-1, 1)), torch.tensor(
        contexts_negatives), torch.tensor(masks), torch.tensor(labels))

• 定义函数读取PTB数据集并返回数据迭代器和词表

def load_data_ptb(batch_size, max_window_size, num_noise_words):
    """下载PTB数据集，然后将其加载到内存中"""
    sentences = read_ptb()
    vocab = d2l.Vocab(sentences, min_freq=10)
    subsampled, counter = subsample(sentences, vocab)
    corpus = [vocab[line] for line in subsampled]
    all_centers, all_contexts = get_centers_and_contexts(corpus, max_window_size)
    all_negatives = get_negatives(all_contexts, vocab, counter, num_noise_words)

    class PTBDataset(torch.utils.data.Dataset):
        def __init__(self, centers, contexts, negatives):
            assert len(centers) == len(contexts) == len(negatives)
            self.centers = centers
            self.contexts = contexts
            self.negatives = negatives

        def __getitem__(self, index):
            return (self.centers[index], self.contexts[index],
                    self.negatives[index])

        def __len__(self):
            return len(self.centers)

    dataset = PTBDataset(all_centers, all_contexts, all_negatives)
    data_iter = torch.utils.data.DataLoader(dataset, batch_size, 
                                    shuffle=True, collate_fn=batchify)
    return data_iter, vocab

• 打印数据迭代器的第一个小批量

data_iter, vocab = load_data_ptb(512, 5, 5)
for batch in data_iter:
    for name, data in zip(names, batch):
        print(name, 'shape:', data.shape)
    break

centers shape: torch.Size([512, 1])
contexts_negatives shape: torch.Size([512, 60])
masks shape: torch.Size([512, 60])
labels shape: torch.Size([512, 60])

四、预训练word2vec

batch_size, max_window_size, num_noise_words = 512, 5, 5
data_iter, vocab = d2l.load_data_ptb(batch_size, max_window_size, num_noise_words)

1.前向传播

在前向传播中，Skip-Gram的输入包括中心词索引center(批量大小，1）和上下文与噪声词索引contexts_and_negatives（批量大小，max_len）。这两个变量首先通过嵌入层从词元索引转换成向量，然后它们的批量矩阵相乘返回形状为（批量大小，1，max_len）的输出。输出中的每个元素是中心词向量和上下文或噪声词向量的点积。

def skip_gram(center, contexts_and_negatives, embed_v, embed_u):
    v = embed_v(center)
    u = embed_u(contexts_and_negatives)
    pred = torch.bmm(v, u.permute(0, 2, 1))
    return pred

2.损失函数

class SigmoidBCELoss(nn.Module):
    """带掩码的二元交叉熵损失"""
    def __init__(self):
        super().__init__()

    def forward(self, inputs, target, mask=None):
        out = F.binary_cross_entropy_with_logits(
            inputs, target, weight=mask, reduction="none")
        return out.mean(dim=1)

loss = SigmoidBCELoss()

• 初始化模型参数

embed_size = 100
net = nn.Sequential(nn.Embedding(num_embeddings=len(vocab),
                                 embedding_dim=embed_size),
                    nn.Embedding(num_embeddings=len(vocab),
                                 embedding_dim=embed_size))

3.训练

def train(net, data_iter, lr, num_epochs, device=d2l.try_gpu()):
    def init_weights(m):
        if type(m) == nn.Embedding:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    net = net.to(device)
    optimizer = torch.optim.Adam(net.parameters(), lr=lr)
    animator = d2l.Animator(xlabel='epoch', ylabel='loss', xlim=[1, num_epochs])
    # 规范化的损失之和，规范化的损失数
    metric = d2l.Accumulator(2)
    for epoch in range(num_epochs):
        timer, num_batches = d2l.Timer(), len(data_iter)
        for i, batch in enumerate(data_iter):
            optimizer.zero_grad()
            center, context_negative, mask, label = [data.to(device) for data in batch]

            pred = skip_gram(center, context_negative, net[0], net[1])
            l = (loss(pred.reshape(label.shape).float(), label.float(), mask)
                     / mask.sum(axis=1) * mask.shape[1])
            l.sum().backward()
            optimizer.step()
            metric.add(l.sum(), l.numel())
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (metric[0] / metric[1],))
    print(f'loss {metric[0] / metric[1]:.3f}, '
          f'{metric[1] / timer.stop():.1f} tokens/sec on {str(device)}')
    
    
lr, num_epochs = 0.002, 5
train(net, data_iter, lr, num_epochs)

4.应用词嵌入

训练word2vec模型之后，可以使用训练好模型中词向量的余弦相似度来从词表中找到与输入单词语义最相似的单词。

def get_similar_tokens(query_token, k, embed):
    W = embed.weight.data
    x = W[vocab[query_token]]
    # 计算余弦相似性。增加1e-9以获得数值稳定性
    cos = torch.mv(W, x) / torch.sqrt(torch.sum(W * W, dim=1) *
                                      torch.sum(x * x) + 1e-9)
    # torch.topk(cos, k=k+1)[1] 返回相似度按降序排列前k+1个对应的索引
    topk = torch.topk(cos, k=k+1)[1].cpu().numpy().astype('int32')
    for i in topk[1:]:  # 删除输入词
        print(f'cosine sim={float(cos[i]):.3f}: {vocab.to_tokens(i)}')

get_similar_tokens('chip', 3, net[0])