关联规则算法——Apriori算法解析及Python实现
文章目录
- 关联规则挖掘过程
- Apriori算法
-
- 1. Apriori算法的基本思想
- 2. Apriori算法产生频繁项集的过程
- 3. Apriori算法的主要步骤
- 4. 举例及代码实现
关联规则挖掘过程
关联规则挖掘问题可以分解为以下两个子问题
- 找频繁项集
找出事务集T中所有大于或等于用户指定最小支持度的项集,即频繁项集。(项集的支持度可简单用包含该项集的事务数来表示) - 利用频繁项集生成所需要的关联规则
对每一频繁项集A,找到A的所有非空子集a,如果support(A) / support(a) >= min_confidence,则a=>(A-a)称为强关联规则。
Apriori算法
通过对数据库的多次扫描来计算项集的支持度,并发现所有的频繁项集从而生成关联规则。1. Apriori算法的基本思想
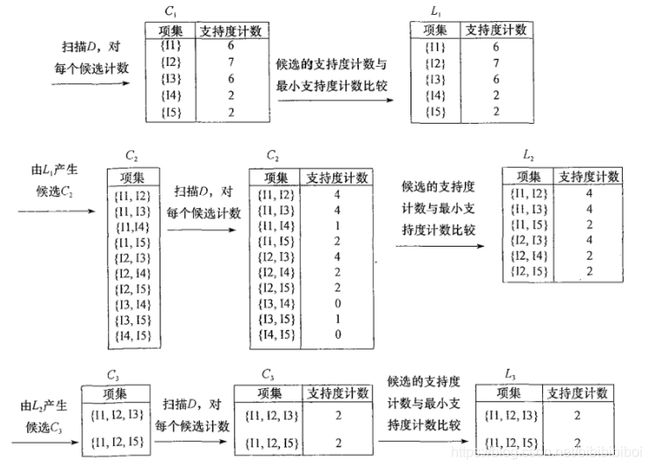
对数据集进行多次扫描,第一次扫描得到频繁1-项集的集合L1,第k次扫描首先利用第k-1次扫描的结果Lk-1产生候选k-项集Ck,在扫描过程中计算Ck的支持度,在扫描结束后计算频繁k-项集Lk,算法当候选k-项集的集合Ck为空的时候结束。
2. Apriori算法产生频繁项集的过程
(1)连接步
(2)剪枝步
3. Apriori算法的主要步骤
(1) 扫描全部数据,产生候选1-项集的集合C1
(2) 根据最小支持度,由候选1-项集的集合C1产生频繁1-项集的集合L1
(3) 对k>1,重复步骤(4)(5)(6)
(4) 由Lk执行连接和剪枝操作,产生候选(k+1)-项集Ck+1
(5) 根据最小支持度,由候选(k+1)-项集的集合Ck+1产生频繁(k+1)-项集的集合Lk+1
(6) 若L不为空集,则k = k+1,跳往步骤(4),否则跳往步骤(7)
(7) 根据最小置信度,由频繁项集产生强关联规则
4. 举例及代码实现
def load_data_set():
"""
加载事务集
"""
data_set = [['l1','l2','l5'],
['l2','l4'],
['l2','l3'],
['l1','l2','l4'],
['l1','l3'],
['l2','l3'],
['l1','l3'],
['l1','l2','l3','l5'],
['l1','l2','l3']]
# data_set = [['l1', 'l2'], ['l1', 'l3', 'l4', 'l5'], ['l2', 'l3', 'l4', 'l6'],
# ['l1', 'l2', 'l3', 'l4'], ['l1', 'l2', 'l3','l6']]
return data_set
def create_C1(data_set):
"""
遍历事务集获得候选1-项集C1
"""
C1 = set() # 集合对象
for t in data_set:
for item in t:
# 将事务集中的每个项集的项转换为不可变的集合
item_set = frozenset([item])
# print(item_set)
C1.add(item_set)
return C1
def is_apriori(Ck_item,Lksub1):
"""
对候选k-项集Ck中的每个项进行剪枝判断
"""
for item in Ck_item:
sub_Ck = Ck_item - frozenset([item])
if sub_Ck not in Lksub1: # 候选k-项集中的项的子集中存在于非频繁k-1 -项集中
return False # 则该项在非频繁k-项集中
return True
def create_Ck(Lksub1,k):
"""
通过Lk-1的连接运算构建候选k-项集Ck,k应该大于2
Lksub1:Lk-1,频繁k-1 -项集
"""
Ck = set()
list_Lksub1 = list(Lksub1)
for i in range(len(Lksub1)):
for j in range(1,len(Lksub1)):
l1 = list(list_Lksub1[i])
l2 = list(list_Lksub1[j])
l1.sort()
l2.sort()
if l1[0:k-2] == l2[0:k-2]: # 排序后做连接运算
Ck_item = list_Lksub1[i] | list_Lksub1[j]
if is_apriori(Ck_item,Lksub1): # 判断是否应该剪枝,是则不加入频繁k-项集
Ck.add(Ck_item)
return Ck
def generate_Lk_by_Ck(data_set,Ck,min_support,support_data):
"""
在Ck中执行删除操作,生成频繁k-项集Lk
support_data: 频繁k-项集对应的支持度
"""
Lk = set()
item_count = {}
for t in data_set:
for item in Ck: # 对Ck中的每个项计算支持度计数
if item.issubset(t):
if item in item_count:
item_count[item] += 1
else:
item_count[item] = 1
t_num = float(len(data_set))
for item in item_count: # 计算每个项的支持度
if(item_count[item]/t_num >= min_support): # 和最小支持度进行比较判断是否为频繁项
Lk.add(item)
support_data[item] = item_count[item] / t_num
return Lk
def generate_L(data_set,min_support):
"""
计算所有的频繁项集
"""
support_data = {}
C1 = create_C1(data_set)
L1 = generate_Lk_by_Ck(data_set,C1,min_support,support_data) # 单独计算C1和L1
Lksub1 = L1.copy()
L = []
L.append(Lksub1)
i = 2
while(True): # 计算Ck
Ci = create_Ck(Lksub1,i)
Li = generate_Lk_by_Ck(data_set,Ci,min_support,support_data)
if len(Li) == 0: # 当Li为空集时退出循环
break;
Lksub1 = Li.copy()
L.append(Lksub1)
i+=1
return L,support_data
def generate_big_rules(L,support_data,min_conf):
"""
找出满足最小置信度的频繁项集
"""
big_rules_list = [] # 强关联规则的列表
sub_set_list = [] # 子集列表
for i in range(0,len(L)): # 对于每个频繁项要产生其非空子集并计算置信度,大于最小置信度则将该强关联规则加入强关联规则的列表中
for freq_set in L[i]: # 频繁1项集里没有强关联
for sub_set in sub_set_list: # 频繁项集的子集一定也是频繁项集
if(sub_set.issubset(freq_set)): # 遍历生成频繁项集freq_set的每个子集
conf = support_data[freq_set] / support_data[sub_set]
big_rule = (sub_set,freq_set - sub_set,conf)
if conf >= min_conf and big_rule not in big_rules_list:
big_rules_list.append(big_rule)
sub_set_list.append(freq_set) # 频繁项集本身也是其子集
return big_rules_list
if __name__ == "__main__":
data_set = load_data_set()
L,support_data = generate_L(data_set,min_support=2/9)
big_rules_list = generate_big_rules(L,support_data,min_conf=0.7)
# 输出
for Lk in L:
print("="*50)
print("frequent " + str(len(list(Lk)[0])) + "-itemsets\tsupport")
print("="*50)
for freq_set in Lk:
print(freq_set,support_data[freq_set])
print("Big Rules:")
for item in big_rules_list:
print(item[0],"==>",item[1]," conf:",item[2])
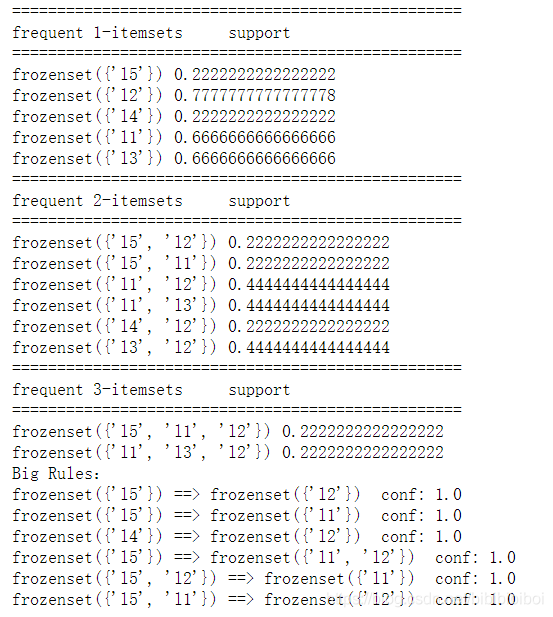
运行结果
实现参考:Apriori算法介绍(Python实现)