Bishop 模式识别与机器学习读书笔记_ch1.2 概率论基础

---

ch1.2 概率论基础

---

1. 概率论的重要作用

---

• 不确定性的作用
  • 不确定性是模式识别领域的一个关键概念。它的产生一方面是来源于对噪声的度量，另一方面是起因于数据集的有限大小。
• 概率论的作用
  • 概率论为不确定性的量化和处理提供了一个框架，是模式识别核心基础之一。
  • 当概率论与决策理论相结合时，它允许我们根据所有可用的信息做出最佳预测，即使这些信息可能不完整或不明确。

---

1.1 从一个小例子到概率基本概念

红蓝两个盒子，红盒子存放 $2$ 个苹果和 $6$ 个桔子，蓝盒子存放 $3$ 个苹果和 $1$ 个桔子。现在假设我们随机选择其中一个盒子，然后从盒子里随机选择一个水果，在观察了它是哪种水果之后，我们把它放在它的盒子里。我们可以想象多次重复这个过程。让我们假设这样做，我们40%的时间选择红色的盒子，60%的时间选择蓝色的盒子，当我们从盒子里取出一个水果时，我们同样有可能选择盒子里的任何一个水果。

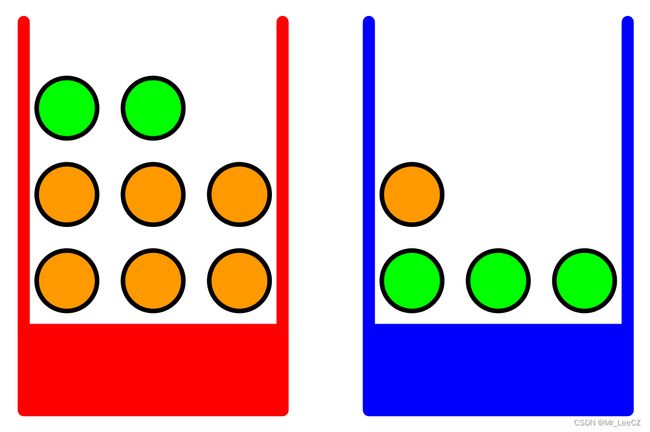
在本例中，将要选择的框的标识是一个随机变量，我们用 $B$ 来表示。这个随机变量可以取两个可能值中的一个，即 $r$（对应于红色框）或 $B$（对应于蓝色框）。同样，水果的特性也是一个随机变量，用 $F$ 表示。它可以取 $a$（苹果）或 $o$（橘子）的任意一个值。

---

1.2 互斥

首先，我们将事件的概率定义为事件发生在试验总数中的分数，在试验总数趋于无穷大的限度内。因此，选择红盒的概率是4/10. 我们把这些概率写成 $p(B=r)=4/10$ 和 $p(B=b）=6/10$. 注意，根据定义，概率必须在区间 $[0,1]$ 内。此外，如果事件是互斥的，并且它们包含所有可能的结果（例如，在本例中盒子必须是红色或蓝色），那么我们看到这些事件的概率必须总和为 1.

---

1.3 加法与乘法规则

我们现在可以问这样的问题：“选择苹果的总体概率是多少？，或者“假设我们选择了一个橙色，那么我们选择的盒子是蓝色的可能性有多大？”. 一旦我们掌握了概率的两个基本规则，即加法规则和乘法规则，我们就可以回答这样的问题，甚至可以回答与模式识别问题相关的更复杂的问题。得到这些规则后，我们将回到我们的水果盒例子。

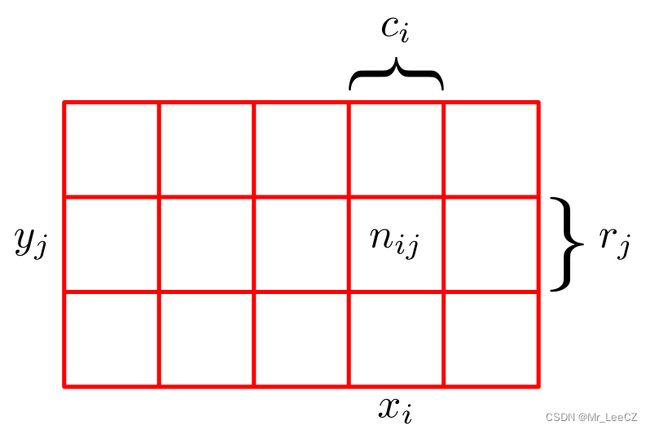
为了推导概率规则，请考虑下图所示的略为一般的例子，其中包含两个随机变量 $X$ 和 $Y$（例如，上面所考虑的盒子和水果变量）。我们假设 $X$ 可以取 $\{x_i|i=1,\cdots ,M\}$ 和 $Y$ 中的任何一个值 $\{y_j|j=1,\cdots ,L\}$. 考虑总共 $N$ 个试验，其中我们对变量 $X$ 和 $Y$ 都进行采样，并让 $X=x_i,Y=y_j$ 中的试验次数为 $n_{ij}$. 此外，让 $X$ 取 $x_i$ 的试验次数（不管Y取多少）用 $c_i$ 表示，同样地让 $Y$ 取 $y_j$ 的试验数用 $r_j$ 表示。

图说明：我们可以通过考虑两个随机变量 $X$ 和 $Y$ 来导出概率和和乘积规则，随机变量 $X$ 的取值为 $\{x_i|i=1,\cdots ,M\}$，随机变量 $Y$ 取值为 $\{y_j|j=1,\cdots ,L\}$. 在这个例子中，我们有 $M=5$ 和 $L=3$. 如果我们考虑这些变量的实例总数 $N$，则可以用 $n_{ij}$ 表示 $X=xi$ 和 $Y=y_j$ 实例数，这是数组对应单元格中的点数。第 $i$ 列 中的点的数目，对应于 $X＝x_i$，用 $c_i$ 表示; 并且第 $j$ 行中的点的数目，对应于 $Y＝y_j$，由 $r_j$ 表示。

---

1.4 联合概率

随机变量 $X$ 取值 $x_i$ 且 随机变量 $Y=y_j$ 的概率表示为 $p(X=x_i,Y=y_j)$，称为 $X=x_i,Y=y_j$ 的联合概率。它是由落在单元格 $i,j$ 中的点数在总数目中的占比得出，因此
$$p(X=x_i,Y=y_j)=\frac{n_{ij}}{N}\text{\hspace{1em}(1)}$$
这里我们隐式地考虑了 $N\to \infty$ 时的极限。当不考虑 $Y$ 的取值而只关注 $X=x_i$ 的概率，可表示为
$$p(X=x_i)=\frac{c_i}{N}\text{\hspace{1em}(2)}$$
或

KaTeX parse error: Undefined control sequence: \notag at position 38: …p(X=x_i,Y=y_j) \̲n̲o̲t̲a̲g̲ ̲
称为概率的加法原则。注意 $p(X=x_i)$ 有时称为边际概率，因为它是通过边缘化或总结出其他变量（在这种情况下是Y）来获得的。

---

1.5 条件概率

在确定随机变量 $X＝x_i$ 的情况下，考虑 $Y＝y_j$ 的概率 $p(Y＝y_j|X＝x_i)$，并且称为给定 $X＝x_i$ 的情况下 $Y＝y_j$ 的条件概率。它是通过求第 $i$ 列中那些落在单元格 $i,j$ 中的点的份数来获得的，因此可表示为
$$p(Y=y_j|X=x_i)=\frac{n_{ij}}{c_i}\text{\hspace{1em}(3)}$$
综合公式（1），（2）和（3），我们可以得到如下关系
KaTeX parse error: Undefined control sequence: \notag at position 105: …\cdot p(X=x_i) \̲n̲o̲t̲a̲g̲ ̲
这就是概率中的乘积法则。

• 加法原则适合边际概率的计算
• 乘法法则适合联合概率或者条件概率的计算

接下来我们将详细介绍概率的加法原则和乘法原则

---

2. 概率的深度应用

---

加法原则： $p(X)={\sum }_{Y}p(X,Y)$

乘法原则： $p(X,Y)=p(Y|X)p(X)$

这里 $p(X,Y)$ 是一个联合概率，被称为“X和Y的概率”。类似地，$p(Y|X)$ 是一个条件概率，称为“Y给定X的概率”，而 $p(X)$ 是边际概率，就是“X的概率”。这两个简单的规则构成了我们在本书中使用的所有概率机制的基础。

由积规则，加上对称性质 $p(X,Y)=p(Y,X)$，我们立即得到条件概率之间的下列关系

$$p(Y|X)=\frac{p(X|Y)\cdot p(Y)}{p(X)}\text{\hspace{1em}(4)}$$
它被称为贝叶斯定理，在模式识别和机器学习中起着核心作用。利用加法法则，贝叶斯定理中的分母可以用分子中出现的量来表示

KaTeX parse error: Undefined control sequence: \notag at position 44: …(X\vert Y)p(Y) \̲n̲o̲t̲a̲g̲ ̲
我们可以将贝叶斯定理中的分母看作是确保（4）的左侧条件概率与Y的所有值之和等于1所需的归一化常数。

---

2.1 一维概率密度

• 除了考虑离散事件集上定义的概率外，我们还希望考虑连续变量的概率。我们将只限于相对非正式的讨论。
• 如果实值变量 $x$ 落入区间 $(x,x+\delta x)$ 中的概率由 $p(x)\delta x$ 表示为 $\delta x\to 0$，则 $p(x)$ 称为 $x$ 上的概率密度。如下图所示。$x$ 在区间 $(a,b)$ 中的概率由

KaTeX parse error: Undefined control sequence: \notag at position 30: …\int_a^bp(x)dx \̲n̲o̲t̲a̲g̲ ̲

因为概率是非负的，而且x的值必须在实轴的某个地方，所以概率密度 $p(x)$ 必须满足这两个条件

KaTeX parse error: Undefined control sequence: \notag at position 13: p(x)\geq 0 \̲n̲o̲t̲a̲g̲ ̲

KaTeX parse error: Undefined control sequence: \notag at position 33: …infty p(x)dx=1 \̲n̲o̲t̲a̲g̲ ̲

累计分布函数可由 $x$ 位于区间 $(－\infty ,z)$ 的概率进行定义，表示为
KaTeX parse error: Undefined control sequence: \notag at position 30: …infty}^zp(x)dx \̲n̲o̲t̲a̲g̲ ̲
满足 $P^{\prime }(x)=p(x)$。

---

2.2 多维概率密度

如果我们有几个连续变量 $x_1,\cdots ,x_D$，由向量 $\mathbf{x}$ 表示，那么我们可以定义一个联合概率密度 $p(\mathbf{x})=p(x_1,\cdots ,x_D)$，这样，$\mathbf{x}$ 落入 $\mathbf{x}$ 的无穷小体积 $\delta \mathbf{x}$ 的概率由 $p(\mathbf{x})d\mathbf{x}$ 给出，这个多维概率密度必须满足
KaTeX parse error: Undefined control sequence: \notag at position 22: …thbf{x})\geq 0 \̲n̲o̲t̲a̲g̲ ̲

KaTeX parse error: Undefined control sequence: \notag at position 51: …)d\mathbf{x}=1 \̲n̲o̲t̲a̲g̲ ̲

注意，如果 $x$ 是一个离散变量，那么 $p(x)$ 有时被称为概率质量函数，因为它可以被视为集中在x的允许值上的一组“概率质量”。

概率的加法与乘法原则，以及贝叶斯定理，同样适用于概率密度的情况，或离散和连续变量的组合。例如，如果 $x$ 和 $y$ 是两个实数变量，那么加法和乘法规则的形式如下
KaTeX parse error: Undefined control sequence: \notag at position 21: …=\int p(x,y)dy \̲n̲o̲t̲a̲g̲ ̲

KaTeX parse error: Undefined control sequence: \notag at position 25: …(y\vert x)p(x) \̲n̲o̲t̲a̲g̲ ̲

---

2.3 期望与方差

概率的最重要的运算之一是求函数的加权平均。在概率分布 $p(x)$ 下，某些函数 $f(x)$ 的平均值称为 $f(x)$ 的期望，并用 $\mathbb{E}[f]$ 表示。

• 对于离散分布，期望表示为
  KaTeX parse error: Undefined control sequence: \notag at position 32: …sum_x p(x)f(x) \̲n̲o̲t̲a̲g̲ ̲
  因此，期望本质上是对 $f(x)$ 做了一个加权平均。

• 在连续变量的情况下，期望值用与相应概率密度有关的积分来表示

KaTeX parse error: Undefined control sequence: \notag at position 32: …int p(x)f(x)dx \̲n̲o̲t̲a̲g̲ ̲

在这两种情况下，如果我们从概率分布或概率密度中得到有限的 $N$ 个点，那么期望可以近似为这些点上的有限求和

KaTeX parse error: Undefined control sequence: \notag at position 52: …{n=1}^N f(x_n) \̲n̲o̲t̲a̲g̲ ̲
这种表示方法是直接取平均，当 $N\to \infty$ 时，其值变得更精确。

---

2.4 条件期望

有时我们会考虑多个变量函数的期望值，在这种情况下，我们可以使用下标来指示哪个变量被平均，例如 ${\mathbb{E}}_x[f(x,y)]$ 表示函数 $f(x,y)$ 关于 $x$ 的平均。需要注意的是 ${\mathbb{E}}_x[f(x,y)]$ 是关于 $y$ 的函数，因为它可以表示为关于条件概率的条件期望
KaTeX parse error: Undefined control sequence: \notag at position 53: …(x\vert y)f(x) \̲n̲o̲t̲a̲g̲ ̲
对于连续变量，有类似的定义

KaTeX parse error: Undefined control sequence: \notag at position 48: …\vert y)f(x)dx \̲n̲o̲t̲a̲g̲ ̲
函数 $f(x)$ 的方差定义为

KaTeX parse error: Undefined control sequence: \notag at position 65: …)]\Big)^2\Big] \̲n̲o̲t̲a̲g̲ ̲
它提供了 $f(x)$ 在其平均值 $E[f(x)]$ 周围有多大的可变性的度量。它也可以表示为

KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ …
特别地，我们可以考虑变量 $x$ 本身的方差，表示为
KaTeX parse error: Undefined control sequence: \notag at position 41: …mathbb{E}[x]^2 \̲n̲o̲t̲a̲g̲ ̲
对于两个随机变量 $x$ 和 $y$, 他们的协方差定义为：
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \text{cov}[x…
同样，两个随机向量 $\mathbf{x}$ 和 $\mathbf{y}$, 他们的协方差定义为：

KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \text{cov}[\ma…
注解：协方差在本质上是向量之间的内积，及两个向量模及夹角余弦的乘积。

2.5 贝叶斯概率

上述观点是从随机的、可重复的事件的频率来看待概率，称之为经典的或经常出现的概率解释。现在我们转向更一般的贝叶斯观点，为概率提供了不确定性的量化方法。

有些不确定事件不能通过多次重复实验来描述，例如月球是否曾经处于绕太阳运行的轨道上，或者北极冰盖是否会在本世纪末消失。但是，对于此类问题我们可以借助人们的经验，希望能够根据新的证据来量化我们的表达功能和作出不确定性的准确度，以及随后能够因此采取最佳行动或决定。这可以通过优雅的，非常普遍的，贝叶斯概率解释来实现。

在模式识别领域，贝叶斯有助于获得一个更一般的概率的观点。考虑第1.1节中讨论的多项式曲线拟合示例。将频率概率的概念应用于观测变量 $t_n$ 的随机值似乎是合理的。然而，我们希望解决并量化模型参数 $w$ 的适当选择所带来的不确定性。我们将从贝叶斯的角度看到，我们可以用概率论的方法来描述模型参数的不确定性，例如模型本身的选择。

贝叶斯定理，其形式为

KaTeX parse error: Undefined control sequence: \notag at position 100: …(\mathcal{D})} \̲n̲o̲t̲a̲g̲ ̲
然后让我们以后验概率的形式观察到 $\mathcal{D}$ 之后评估 $\mathbf{w}$ 的不确定性。

对于观测数据集 $\mathcal{D}$，贝叶斯定理右侧的量 $p(\mathcal{D}|\mathbf{w})$ 被视为参数向量 $\mathbf{w}$ 的函数，称为似然函数。它表示观测数据集对于参数向量 $\mathbf{w}$ 不同设置的可能性。注意，似然不是 $\mathbf{w}$ 上的概率分布，其相对于 $\mathbf{w}$ 的积分不一定等于 1。

给出了似然的定义，我们可以用语言来表述贝叶斯定理

KaTeX parse error: Undefined control sequence: \notag at position 63: …es\text{prior} \̲n̲o̲t̲a̲g̲ ̲
当所有这些量都被视为 $\mathbf{w}$ 的函数时，贝叶斯公式中的分母是标准化常数，它确保左侧的后验分布是一个有效的概率密度，并积分为 1。实际上，将贝叶斯公式的两边与关于 $\mathbf{w}$ 积分，我们可以用先验分布和似然函数来表示贝叶斯定理中的分母
KaTeX parse error: Undefined control sequence: \notag at position 77: …w})d\mathbf{w} \̲n̲o̲t̲a̲g̲ ̲
在贝叶斯范式和频率主义范式中，似然函数 $p(\mathcal{D}|\mathbf{w})$ 起着中心作用。然而，在这两种方法中，它的使用方式有着根本的不同。在频率范式中， $\mathbf{w}$ 被认为是固定参数，其值由某种形式的“估计器”确定，这个估计误差是通过考虑可能的数据集 $\mathcal{D}$ 的分布来获得的。相比之下，从贝叶斯的观点来看，只有一个数据集 $\mathcal{D}$（即实际观察到的数据集），参数的不确定性通过 $\mathbf{w}$ 上的概率分布来表示。

一个广泛使用的频率估计是最大似然估计，其中 $\mathbf{w}$ 被设置为使似然函数 $p(\mathcal{D}|\mathbf{w})$ 最大化的值，即
$${\mathbf{w}}^{\ast }=\underset{\mathbf{w}}{\max }p(\mathcal{D}|\mathbf{w})$$
在机器学习文献中，似然函数的负对数称为误差函数或能量函数。由于似然函数通常是连乘的形式，为了克服不易求导的问题，利用函数的单调性设置为对数形式，又考虑到目标函数通常为正数，故把公式(1)设置成
$${\mathbf{w}}^{\ast }=\underset{\mathbf{w}}{\max }p(\mathcal{D}|\mathbf{w})=\underset{\mathbf{w}}{\min }-\log p(\mathcal{D}|\mathbf{w})$$
因此，最大似然等于最小化误差。

确定频率误差条的一种方法是bootstrap（自助法**，是一种再抽样的统计方法），其中创建了如下多个数据集。假设原始数据集由 $N$ 个数据点 $X=\{{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N\}$ 组成。我们可以从 $X$ 中有放回随机抽取 $N$ 个点创建一个新的数据集 $X_B$ ，这样 $X$ 中的某些点在 $X_B$ 中是重复的，而 $X$ 中的其他点可能不在 $X_B$中。这个过程可以重复 $L$ 次，以生成 $L$ 个数据集，每个数据集大小为 $N$，每个数据集通过从原始数据集 $X$ 采样获得。然后，通过观察不同 bootstrap 数据集之间预测的可变性来评估参数估计的统计准确性。自助法的关键所在是自助统计量与观察统计量间的关系，就如同观察统计量与真值间的关系。

---

2.6 贝叶斯的说明

• 过分地依赖先验会导致极端的结果，如掷硬币前三次为正面，则判断后续均为正面
• 利用贝叶斯解决问题尽量寻找合适的先验或者弱先验

---

3. 高斯分布

---

3.1 单变量高斯分布

连续随机变量是一类重要的概率分布，以高斯分布最为著名。对于单实值变量 $x$，高斯分布定义为
KaTeX parse error: Undefined control sequence: \notag at position 116: …x-\mu)^2\Big\} \̲n̲o̲t̲a̲g̲ ̲
其中决定分布形式的两个参数有两个：$\mu$ 称为均值，${\sigma }^2$ 称为方差。方差的平方根 $\sigma$ 称为标准差，方差的倒数 $\beta =\frac{1}{{\sigma }^2}$ 称为精确度。

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import seaborn as sns
sns.set(style="darkgrid")

mu_params = [-1, 0, 1] # 均值
sd_params = [0.5, 1, 1.5] # 方差
x = np.linspace(-7, 7, 100) # 随机变量 x
f, ax = plt.subplots(len(mu_params), len(sd_params), sharex=True, sharey=True, dpi=260)
for i in range(3):
    for j in range(3):
        mu = mu_params[i]
        sd = sd_params[j]
        y = stats.norm(mu, sd).pdf(x) # 连续随机变量的概率分布函数
        ax[i,j].plot(x, y)
        ax[i,j].plot(0, 0,
        label="$\\mu$ = {:3.2f}\n$\\sigma$ = {:3.2f}".format(mu, sd), alpha=0)
        ax[i,j].legend(fontsize=6)
ax[2,1].set_xlabel('$x$', fontsize=16)
ax[1,0].set_ylabel('$pdf(x)$', fontsize=16)
plt.xticks(np.arange(-8,10,2))
plt.yticks(np.arange(0,1,0.2))
plt.tight_layout()
plt.show()

由高斯概率密度函数可知

KaTeX parse error: Undefined control sequence: \notag at position 40: …sigma^2)\geq 0 \̲n̲o̲t̲a̲g̲ ̲

KaTeX parse error: Undefined control sequence: \notag at position 59: …,\sigma^2)dx=1 \̲n̲o̲t̲a̲g̲ ̲

因为设$I={\int }_{-\infty }^{\infty }\exp \{-\frac{(x-\mu {)}^2}{2{\sigma }^2}\}dx$，则$I^2={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\exp \{-\frac{(x-\mu {)}^2}{2{\sigma }^2}-\frac{(y-\mu {)}^2}{2{\sigma }^2}\}dxdy$，

令$x-\mu =r\cos \theta$，$y-\mu =r\sin \theta$，则$I^2={\int }_0^{2\pi }d\theta {\int }_0^{\infty }\exp \{-\frac{r^2}{2{\sigma }^2}r\}dr=2\pi {\sigma }^2$，

所以，$I=\sqrt{2\pi {\sigma }^2}$，即${\int }_{-\infty }^{\infty }\mathcal{N}(x|\mu ,{\sigma }^2)dx=1$

在高斯分布下，我们很容易找到随机变量 $x$ 的期望值，即 x 的平均值为
KaTeX parse error: Undefined control sequence: \notag at position 76: …igma^2)xdx=\mu \̲n̲o̲t̲a̲g̲ ̲
因为$\mathbb{E}[x]={\int }_{-\infty }^{\infty }\frac{1}{\sqrt{2\pi {\sigma }^2}}x\exp \{-\frac{(x-\mu {)}^2}{2{\sigma }^2}\}dx$，令$x-\mu =y$，则$\mathbb{E}[x]={\int }_{-\infty }^{\infty }\frac{1}{\sqrt{2\pi {\sigma }^2}}y\exp \{-\frac{y^2}{2{\sigma }^2}\}dy+{\int }_{-\infty }^{\infty }\frac{\mu }{\sqrt{2\pi {\sigma }^2}}\exp \{-\frac{y^2}{2{\sigma }^2}\}dy=0+\mu =\mu$

因为参数 $\mu$ 表示分布下 $x$ 的平均值，所以称为平均值。同样，对于二阶矩
KaTeX parse error: Undefined control sequence: \notag at position 91: …\mu^2+\sigma^2 \̲n̲o̲t̲a̲g̲ ̲
则在正态分布下，随机变量 $x$ 的方差为

KaTeX parse error: Undefined control sequence: \notag at position 57: …[x]^2=\sigma^2 \̲n̲o̲t̲a̲g̲ ̲
因此，${\sigma }^2$ 被称为方差参数。分布的最大值点称为其模式。对于高斯，模式与平均值一致。

---

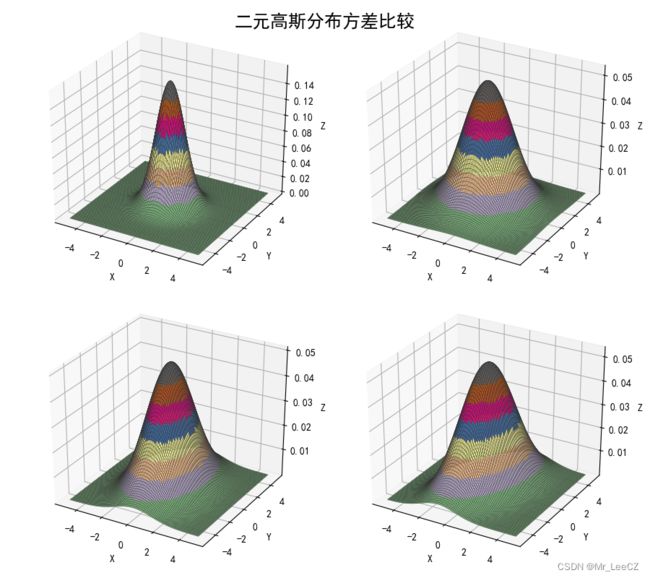
3.2 多维高斯函数分布

对于多维连续随机变量 $\mathbf{x}$，其高斯分布形式定义为：

KaTeX parse error: Undefined control sequence: \notag at position 230: …bf{\mu})\Big\} \̲n̲o̲t̲a̲g̲ ̲
其中，$D$ 维向量 $\mu$ 被称为平均值，$D\times D$ 矩阵 $\mathbf{\Sigma }$ 被称为协方差，而 $|\mathbf{\Sigma }|$ 表示 $\mathbf{\Sigma }$ 的行列式。

#!/usr/bin/python
#  -*- coding:utf-8 -*-

import numpy as np
from scipy import stats
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm


if __name__ == '__main__':
    x1, x2 = np.mgrid[-5:5:51j, -5:5:51j]
    x = np.stack((x1, x2), axis=2)
    print('x1 = \n', x1)
    print('x2 = \n', x2)
    print('x = \n', x)

    mpl.rcParams['axes.unicode_minus'] = False
    mpl.rcParams['font.sans-serif'] = 'SimHei'
    plt.figure(figsize=(9, 8), facecolor='w')
    sigma = (np.identity(2), np.diag((3,3)), np.diag((2,5)), np.array(((2,1), (1,5))))
    for i in np.arange(4):
        ax = plt.subplot(2, 2, i+1, projection='3d')
        norm = stats.multivariate_normal((0, 0), sigma[i])
        y = norm.pdf(x)
        ax.plot_surface(x1, x2, y, cmap=cm.Accent, rstride=1, cstride=1, alpha=0.9, lw=0.3, edgecolor='#303030')
        ax.set_xlabel('X')
        ax.set_ylabel('Y')
        ax.set_zlabel('Z')
    plt.suptitle('二元高斯分布方差比较', fontsize=18)
    plt.tight_layout(1.5)
    plt.show()

---

3.3 高斯分布的极大似然估计

现在假设我们有一组观测值 $\mathbf{x}=(x_1,\cdots ,x_N{)}^T$，表示标量变量 $x$ 的 $N$ 个观测值。假设观测值是从均值为 $\mu$ 和方差 ${\sigma }^2$​ 未知的高斯分布抽样得到的，我们希望从数据集中确定这些参数。观测样本是从同一分布中独立抽取得到的称为独立同分布，通常缩写为 $i.i.d$. 我们已经看到，两个独立事件的联合概率分别由每个事件的边际概率的乘积给出。因为我们的数据集 $x$ 是 $i.i.d.$，所以我们可以将给定 $\mu$ 和 ${\sigma }^2$ 的数据集的概率表示为

KaTeX parse error: Undefined control sequence: \notag at position 82: …t\mu,\sigma^2) \̲n̲o̲t̲a̲g̲ ̲
可以看作是 $\mu$ 和 ${\sigma }^2$ 的函数，是高斯函数的似然函数。

我们将通过最大化似然函数来确定高斯函数中未知参数 $\mu$ 和 ${\sigma }^2$ 的值。根据公式（2），极大似然等价于极小化负log 似然，表示为

KaTeX parse error: Undefined control sequence: \notag at position 148: …N}{2}\ln(2\pi) \̲n̲o̲t̲a̲g̲ ̲
关于 $\mu$ 求 log 似然的极大值，得

$${\mu }_{ML}=\frac{1}{N}\sum _{n=1}^N{x}_n$$
这是样本平均值，即观测值 $x_n$ 的平均值。类似地，求关于 ${\sigma }^2$ 求 log 似然的极大值解，得

$${\sigma }_{ML}^2=\frac{1}{N}\sum _{n=1}^N(x_n-{\mu }_{ML}{)}^2$$

通过极大似然（3）和（4），我们可以估计抽样样本的均值和方差。如果由抽样多个样本形成样本空间，这些样本的统计量能否估计总体的统计量？这就需要看一下抽样分布，利用抽样分布的统计量估计总体的统计量，可验证一阶矩（期望，均值）。样本均值的期望为
KaTeX parse error: Undefined control sequence: \notag at position 27: …[\mu_{ML}]=\mu \̲n̲o̲t̲a̲g̲ ̲
而样本方差的期望为
$$\mathbb{E}[{\sigma }_{ML}^2]=(\frac{N-1}{N}){\sigma }^2$$
注解：极大似然方法获取的是抽样样本的统计量，不是总体的统计量。

推导： $\mathbb{E}[{\mu }_{ML}]=\mu$
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \mathbb{E}[\mu…
推导： $\mathbb{E}[{\sigma }_{ML}^2]=(\frac{N-1}{N}){\sigma }^2$

KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \mathbb{E}[\si…
由公式 （5）可以，若想获取方差的无偏统计量 ${\sigma }^2$，需要添加一个合适的系数
KaTeX parse error: Undefined control sequence: \notag at position 149: …x_n-\mu_{ML})^2\̲n̲o̲t̲a̲g̲ ̲
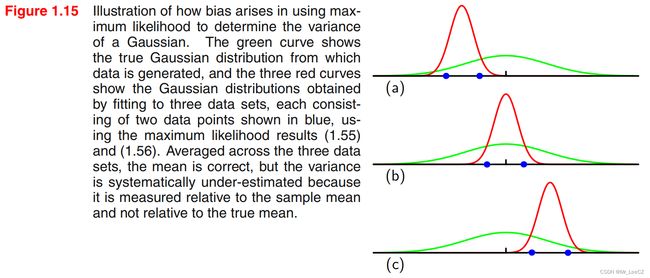
例：假设总体分布是高斯分布 $N(0,1.5)$，分布如图 1.15 绿色曲线所示, 每次从总体中采样 2 个数据点

（图中蓝色点所示），形成 3 个样本，样本分布曲线如图 1.15 红色曲线所示。根据极大似然方法（3）和（4）求出样本均值和方差分别为

​ ${\mu }_1=-a,{\mu }_2=0,{\mu }_1=a$; ${\sigma }_1^2={\sigma }_2^2={\sigma }_3^2=1$

对 3 个数据集的平均值求期望（平均）得 $\mu =(-a+0+a)/3=0$, 与总体均值相同；而三个数据集的方差的期望（平均）${\sigma }^2=({\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2)/3=1$，与总体方差相比是有偏差的，为有偏估计。

注解：当数据点的数量 $N$ 增大时，最大似然解的偏移会变得不太重要，并且在 $N$ 趋于无穷大的情况下，方差的最大似然节与产生数据的分布的真实方差相等。但是，在带有很多参数的复杂模型，最大似然的偏移问题会非常严重，在多项式曲线拟合问题中，最大似然的偏移问题是过拟合问题的主要影响因素。

4. 概率分布的应用

---

多项式曲线拟合的问题可以通过误差最小化问题来表示。这里我们从概率的角度来考察它，并且可以更深刻地认识误差函数和正则化，并且能够完全从贝叶斯的角度来看待这个问题。

---

4. 1 重新审视曲线拟合

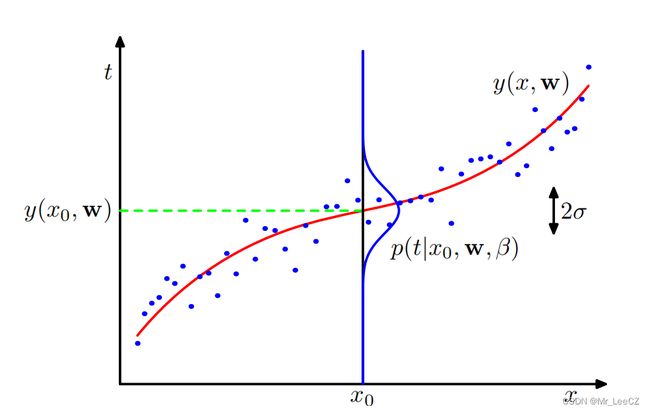
曲线拟合问题的目标是能够在一组训练数据的基础上，对给定输入变量 $x$ 的新值的目标变量 $t$ 进行预测，这些数据包括 $N$ 个输入值 $\mathbf{x}=(x_1,\cdots ,x_N{)}^T$ 和它们对应的目标值 $\mathbf{t}=(t_1,\cdots ,t_N{)}^T$. 我们可以使用概率分布表示我们对目标变量值的不确定性。为此，我们假设，给定 $x$ 的值，$t$ 的相应值具有高斯分布，其平均值等于拟合多项式曲线的函数值 $y(x,\mathbf{w})$. 所以我们有

KaTeX parse error: Undefined control sequence: \notag at position 80: …}),\beta^{-1}) \̲n̲o̲t̲a̲g̲ ̲
其中，$\beta$ 为方差的逆，称为精度。曲线拟合示意图如下

我们现在使用训练数据 $\{\mathbf{x},\mathbf{t}\}$ 来确定未知参数 $\mathbf{w}$ 和 $\beta$ 的最大似然值。如果假设数据服从高斯分布，且是独立同分布得，则似然函数为

KaTeX parse error: Undefined control sequence: \notag at position 113: …}),\beta^{-1}) \̲n̲o̲t̲a̲g̲ ̲
取 log 函数得

KaTeX parse error: Undefined control sequence: \notag at position 150: …N}{2}\ln(2\pi) \̲n̲o̲t̲a̲g̲ ̲
由于上式等式右端后两项关于参数 $\mathbf{w}$ 为常数，不影响 log 似然函数求极值，因此其和极小化平方误差函数是一致的。因此，在高斯噪声分布的假设下，平方误差函数之和是最大似然的结果。

我们可以通过求导获得 $\mathbf{w}$ 的解，同时，我们也可以获得参数 $\beta$ 的解
KaTeX parse error: Undefined control sequence: \notag at position 79: …_{ML})-t_n\}^2 \̲n̲o̲t̲a̲g̲ ̲
在确定了参数 $\mathbf{w}$ 和 $\beta$ 之后，我们现在可以对 $x$ 的新值进行预测。因为我们现在有一个概率模型，它们用给出 $t$ 上概率分布的预测分布来表示，而不是简单的点估计，通过将最大似然参数代入 $p(t|x,\mathbf{w},\beta )=\mathcal{N}(t|y(x,\mathbf{w}),{\beta }^{-1})$ 得到
KaTeX parse error: Undefined control sequence: \notag at position 100: …eta_{ML}^{-1}) \̲n̲o̲t̲a̲g̲ ̲
现在让我们朝着更深层的贝叶斯方法迈出一步，并在多项式系数 $\mathbf{w}$ 上引入先验分布。为了简单起见，我们依然用最简单的高斯分布作为参数先验分布
KaTeX parse error: Undefined control sequence: \notag at position 183: …^T\mathbf{w}\} \̲n̲o̲t̲a̲g̲ ̲
其中，$\alpha$ 为先验高斯分布的精度，$M+1$ 为参数 $\mathbf{w}$ 的元素个数。利用贝叶斯框架可获取参数 $\mathbf{w}$ 的后验分布
KaTeX parse error: Undefined control sequence: \notag at position 136: …}\vert \alpha) \̲n̲o̲t̲a̲g̲ ̲
我们现在可以通过找到给定数据的 $\mathbf{w}$ 的最可能值来确定 $\mathbf{w}$ ，换句话说，通过最大化后验分布来确定。这种技术被称为最大后验，或简称MAP. 极大后验等价于极小化下式
KaTeX parse error: Undefined control sequence: \notag at position 130: …thbf{w}\Bigg\} \̲n̲o̲t̲a̲g̲ ̲
因此，我们看到，最大化后验分布等价于最小化平方误差函数的正则化和，正则化参数由λ=α/β给出。

注解：值得注意的是，后验分布是关于参数的一个分布，而不是一个值，需要找到最可能的值是它的众数，及分布的极值点，也就是模式，这也是模式识别的由来。

---

4.2 贝叶斯曲线拟合

问题：

• 尽管我们已经包含了先验分布 $p(\mathbf{w}|\alpha )$，但到目前为止，我们仍在对 $\mathbf{w}$ 进行点估计，因此这还不等于贝叶斯处理。
• 在完全贝叶斯方法中，我们应该始终如一地应用概率的加法与乘法规则，这就要求，正如我们将很快看到的那样，我们对 $\mathbf{w}$ 的所有值进行积分。这种边缘化是模式识别贝叶斯方法的核心。

在曲线拟合问题中，我们给出了训练数据 $\mathbf{X}$ 和 $\mathbf{t}$ ，以及一个新的测试点 $x$，我们的目标是预测 $t$ 的值，因此我们希望评估预测分布 $p(t|x，\mathbf{X}，\mathbf{t})$. 这里我们假设参数 $\alpha$ 和 $\beta$ 是固定的和已知的。

贝叶斯处理模式简单地对应于概率的加法和乘法规则的综合应用，它允许将预测分布写成
KaTeX parse error: Undefined control sequence: \notag at position 178: …})d \mathbf{w} \̲n̲o̲t̲a̲g̲ ̲
其中 $p(t|x,\mathbf{w},\beta )=\mathcal{N}(t|y(x,\mathbf{w}),{\beta }^{-1})$，由于 $\alpha$ 和 $\beta$ 已知，简写为 $p(t|x,\mathbf{w})=\mathcal{N}(t|x,\mathbf{w})$；后验概率 $p(\mathbf{w}|\mathbf{X},\mathbf{t})$ 可利用前述公式 $p(\mathbf{w}|\mathbf{X},\mathbf{t})\propto p(\mathbf{t}|\mathbf{X},\mathbf{w})p(\mathbf{w})$ 的等式右侧部分。因此上式可解析地给出结果的高斯分布预测形式
KaTeX parse error: Undefined control sequence: \notag at position 68: …t m(x),s^2(x)) \̲n̲o̲t̲a̲g̲ ̲
其中，
KaTeX parse error: Undefined control sequence: \notag at position 57: …N \phi(x_n)t_n \̲n̲o̲t̲a̲g̲ ̲

KaTeX parse error: Undefined control sequence: \notag at position 47: …thbf{S}\phi(x) \̲n̲o̲t̲a̲g̲ ̲

矩阵 $\mathbf{S}$ 表示为
KaTeX parse error: Undefined control sequence: \notag at position 72: …(x_n)\phi(x)^T \̲n̲o̲t̲a̲g̲ ̲
其中 $\mathbf{I}$ 是单位矩阵，我们定义了向量 $\varphi (x{)}^T$ ，元素 ${\varphi }_i(x{)}^T=x^i$ , $i=1,\cdots ,M.$

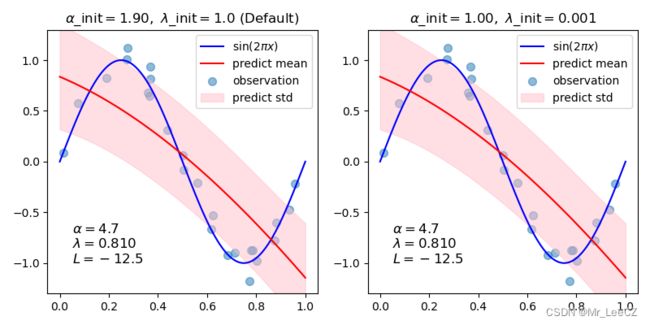
同样，我们可以采用贝叶斯回归的方法来获得好的拟合效果。在本部分我们只展示一下例子，在下一章节学习了概率论和贝叶斯之后再详细讨论其原理

# Author: Yoshihiro Uchida 

import numpy as np
import matplotlib.pyplot as plt

from sklearn.linear_model import BayesianRidge


def func(x): return np.sin(2*np.pi*x)

# #############################################################################
# Generate sinusoidal data with noise
size = 25
rng = np.random.RandomState(1234)
x_train = rng.uniform(0., 1., size)
y_train = func(x_train) + rng.normal(scale=0.1, size=size)
x_test = np.linspace(0., 1., 100)


# #############################################################################
# Fit by cubic polynomial
n_order = 3
X_train = np.vander(x_train, n_order + 1, increasing=True)
X_test = np.vander(x_test, n_order + 1, increasing=True)

# #############################################################################
# Plot the true and predicted curves with log marginal likelihood (L)
reg = BayesianRidge(tol=1e-6, fit_intercept=False, compute_score=True)
fig, axes = plt.subplots(1, 2, figsize=(8, 4))
for i, ax in enumerate(axes):
    # Bayesian ridge regression with different initial value pairs
    if i == 0:
        init = [1 / np.var(y_train), 1.]  # Default values
    elif i == 1:
        init = [1., 1e-3]
#        reg.set_params(alpha_init=init[0], lambda_init=init[1])
    reg.fit(X_train, y_train)
    ymean, ystd = reg.predict(X_test, return_std=True)

    ax.plot(x_test, func(x_test), color="blue", label="sin($2\\pi x$)")
    ax.scatter(x_train, y_train, s=50, alpha=0.5, label="observation")
    ax.plot(x_test, ymean, color="red", label="predict mean")
    ax.fill_between(x_test, ymean-ystd, ymean+ystd,
                    color="pink", alpha=0.5, label="predict std")
    ax.set_ylim(-1.3, 1.3)
    ax.legend()
    title = "$\\alpha$_init$={:.2f},\\ \\lambda$_init$={}$".format(
            init[0], init[1])
    if i == 0:
        title += " (Default)"
    ax.set_title(title, fontsize=12)
    text = "$\\alpha={:.1f}$\n$\\lambda={:.3f}$\n$L={:.1f}$".format(
           reg.alpha_, reg.lambda_, reg.scores_[-1])
    ax.text(0.05, -1.0, text, fontsize=12)

plt.tight_layout()
plt.show()

拟合效果如图

---

5. 小结

本小节介绍了机器学习中概率相关的基础性概念。除线性代数外，概率论与梳理统计在机器学习中占有非常重要的位置，因为机器学习中的建模对象是随机变量。变量的随机使得期望或者均值运算显得特别重要，同样模型的稳定性和显著性、参数的显著性的主题地位也得以显示。