hdu 4686 Arc of Dream(矩阵快速幂）

链接：http://acm.hdu.edu.cn/showproblem.php?pid=4686

题意：

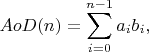
其中a₀ = A0
a_i = a_i-1*AX+AY
b₀ = B0
b_i = b_i-1*BX+BY

最后的结果mod 1,000,000,007

n<=10^18.

分析：ai*bi=(ai-1 *ax+ay)*(bi-1 *bx+by)

                =(ai-1 * bi-1 *ax*bx)+(ai-1 *ax*by)+(bi-1 *bx*ay)+(ay*by)

设p=ax*bx,  q=ax*by,  r=ay*bx,  s=ay*by

所以ai*bi=p(ai-1 * bi-1)+q(ai-1)+r(bi-1)+s

虽然可以用递推来求出每一项，但是n太大了，直接求绝对会超时的。

设f(n)=an*bn,  a(n)=an,  b(n)=bn

s(n)=sum(ai*bi),i=0,1,...n

则f(i)=p*f(i-1)+q*a(i-1)+r*b(i-1)+s

这是一个递推式，对于任何一个递推式，我们都可以用矩阵法来优化，加快速度求出第n项或前n项和。

我们可以构造一个5*5的矩阵A，使得

【f(n-1),a(n-1),b(n-1),1,s(n-2)】*A=【f(n),a(n),b(n),1,s(n-1)】

=【p*f(n-1)+q*a(n-1)+r*b(n-1)+s, a(n-1)*ax+ay, b(n-1)*bx+by, 1, s(n-2)+f(n-1)】

所以我们容易得出矩阵A： 【   axbx    0   0   0   1

                                          axby   ax   0   0   0

                                          aybx    0   bx  0   0

                                         ayay   ay  by   1   0

                                         0         0    0    0   1 】

由【f(1), a(1) ,b(1), 1, s(0)】*A = 【f(2), a(2), b(2), 1, s(1)】

以此类推得，【f(1), a(1) ,b(1), 1, s(0)】*A^(n-1) = 【f(n), a(n), b(n), 1, s(n-1)】

这样就可以快速的求出s(n-1)了，

其中f(1)=a1*b1, a(1)=a0*ax+ay,

b(1)=b0*bx+by, s(0)=a0*b0

接下来就是矩阵快速幂了。

注意：n==0时，直接输出0，不然会死循环TLE的，还有就是要用long long,也要记得mod

AC代码如下：

 1 #include<stdio.h>

 2 #include<string.h>

 3 //#define LL __int64

 4 #define LL long long

 5 #define M 1000000007

 6 struct Matrix

 7 {

 8     LL a[6][6];

 9 }origin,res,tmp,A,ans;

10 int n;

11 Matrix mul(Matrix x,Matrix y)

12 {

13     int i,j,k;

14     memset(tmp.a,0,sizeof(tmp.a));

15     for(i=1;i<=n;i++)

16         for(j=1;j<=n;j++)

17             for(k=1;k<=n;k++)

18             {

19                 tmp.a[i][j]+=(x.a[i][k]*y.a[k][j])%M;

20                 tmp.a[i][j]%=M;

21             }

22     return tmp;

23 }

24 void quickpow(LL k)

25 {

26     int i;

27     memset(res.a,0,sizeof(res.a));

28     for(i=1;i<=n;i++)

29         res.a[i][i]=1;

30     while(k)

31     {

32         if(k&1)

33             res=mul(res,A);

34         A=mul(A,A);

35         k>>=1;

36     }

37 }

38 int main()

39 {

40     LL N,a0,ax,ay,b0,bx,by;

41     LL f1,a1,b1,s0;

42 //    while(scanf("%I64d %I64d %I64d %I64d %I64d %I64d %I64d",&N,&a0,&ax,&ay,&b0,&bx,&by)!=EOF)

43     while(scanf("%lld %lld %lld %lld %lld %lld %lld",&N,&a0,&ax,&ay,&b0,&bx,&by)!=EOF)

44     {

45         if(N==0)

46         {

47             printf("0\n");

48             continue;

49         }

50         a1=(a0*ax+ay)%M;

51         b1=(b0*bx+by)%M;

52         f1=(a1*b1)%M;

53         s0=(a0*b0)%M;

54         n=5;

55         memset(origin.a,0,sizeof(origin.a));

56         origin.a[1][1]=f1;

57         origin.a[1][2]=a1;

58         origin.a[1][3]=b1;

59         origin.a[1][4]=1;

60         origin.a[1][5]=s0;

61         memset(A.a,0,sizeof(A.a));

62         A.a[1][1]=(ax*bx)%M;

63         A.a[1][5]=1;

64         A.a[2][1]=(ax*by)%M;

65         A.a[2][2]=ax%M;

66         A.a[3][1]=(ay*bx)%M;

67         A.a[3][3]=bx%M;

68         A.a[4][1]=(ay*by)%M;

69         A.a[4][2]=ay%M;

70         A.a[4][3]=by%M;

71         A.a[4][4]=1;

72         A.a[5][5]=1;

73 

74         quickpow(N-1);

75         ans=mul(origin,res);

76     //    printf("%I64d\n",ans.a[1][5]);

77         printf("%lld\n",ans.a[1][5]);

78     }

79     return 0;

80 }

View Code