论文笔记系列：经典主干网络（一）-- VGG

 ✨写在前面：强烈推荐给大家一个优秀的人工智能学习网站，内容包括人工智能基础、机器学习、深度学习神经网络等，详细介绍各部分概念及实战教程，通俗易懂，非常适合人工智能领域初学者及研究者学习。➡️点击跳转到网站。

---

深度卷积神经网络VGG

前言：VGGNet 是由牛津大学视觉几何小组（Visual Geometry Group, VGG）提出的一种深层卷积网络结构，他们以 7.32% 的错误率赢得了 2014 年 ILSVRC 分类任务的亚军（冠军由 GoogLeNet 以 6.65% 的错误率夺得）和 25.32% 的错误率夺得定位任务（Localization）的第一名（GoogLeNet 错误率为 26.44%）。VGG可以看成是加深版本的AlexNet，都是conv layer + FC layer。

 论文地址：https://arxiv.org/abs/1409.1556

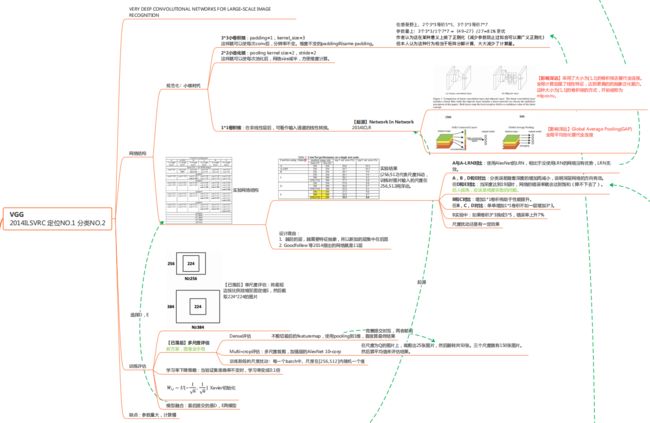
VGG框架导图：

 VGG结构介绍:

     为了解决初始化（权重初始化）等问题，VGG采用的是一种Pre-training的方式，先训练浅层的的简单网络 VGG11，再复用 VGG11 的权重来初始化 VGG13，如此反复训练并初始化 VGG19，能够使训练时收敛的速度更快。整个网络都使用卷积核尺寸为 3×3 和最大池化尺寸 2×2。比较常用的VGG-16的16指的是conv+fc的总层数是16，不包括max pool的层数。

​

VGG论文 

摘要： 介绍网络深度与精度之间的联系，提出深度卷积模型

1. Introduction： Convnet的成功得益于大量数据及高性能GPU；介绍本论文主要贡献

2. ConvNet Configurations： 讲解11-19层的VGG网络结构；3*3卷积与5*5/7*7卷积的感受野等价

3. Classification Framework： VGG网络的分类实验，训练及测试详细步骤；Multi-scale训练，Multi crop/Dense 测试

4. Classification Experiments： 多种设置下的分类结果对比；单尺度评估，多尺度评估，多次裁剪评估，模型融合，最优模型对比

5. Conclusion： 强调深度对convnet是有益的，本文提出的VGG模型获得优异结果

一、VGG模型结构

模型结构设计的特点

小卷积核，堆叠使用卷积核，分辨率减半，通道数翻倍

3x3卷积的优点：

多个3×3的卷积层比一个大尺寸的filter有更少的参数，假设卷基层的输入和输出的特征图大小相同为C，那么三个3×3的卷积层参数个数3×（3×3×C×C）=27CC；一个7×7的卷积层参数为49CC；所以可以把三个3×3的filter看成是一个7×7filter的分解（中间层有非线性的分解）

①体系结构（论文中的2.1）

输入的尺寸是固定的224×224；

预处理方式：每个像素分别减去 RGB三个通道均值，可以加速模型的训练；

卷积层：小卷积核3×3，也尝试了1×1卷积（借鉴了NIN）。卷积不改变分辨率，会用padding填充像素；

池化层：使用5个池化，每个池化用2×2的池化窗口，步长为2，分辨率降低了一半。224×224经过5次池化后，输出为7×7 （因为224/32=7），再拉成一个向量的形式接入FC层；

全连接层：前两个层各有4096个通道，第三层执行1000路分类；

在隐藏层配备了ReLU，没有使用LRN，是因为不能提升性能，哈辉导致内存消耗和计算时间的增加。

②配置（论文中的2.2）

从A->E，网络的深度从11个权值层（8个卷积层+3个全连接层）到19个权值层（16个卷积层+3个全连接层），卷积核数量从64-512。

每经过一次池化，卷积核数量就乘以2。（因为池化后减少了一半的分辨率，信息减少了，所以要用更多的卷积核 得到更多的特征图，把丢失的信息补充回来，不至于信息数据减少的太少了）

网络深度从11-19层，但参数并没有变得很多。

③结构特点的探讨（论文中的2.3）

堆叠使用3×3卷积的好处（每一段对应一个）：

可以增大感受野。感受野等价，2个3×3堆叠等价于一个5×5；3个3×3堆叠等价于1个7×7。

减少训练参数。3个3×3比1个7×7节省81%参数，卷积参数计算公式 3（3²C²）=27C²；7²C²=49C²，（49-27）/27=81%，所以参数量增加81%

采用1×1卷积核的好处，增加了非线性的能力（特征提取的能力），可以增加特征抽象能力，提升模型效果。根据NIN借鉴的。

④表格分析

    VGGNet有两种结构，分别为16层和19层。从下图中可以看出，在VGGNet结构中，所有卷积层的卷积核尺寸都只有(3，3)。VGGNet中连续使用3组(3，3)卷积核(滑动步长为1)是因为它和使用1个(7，7)卷积核产生的效果相同(图5-6以一维卷积为例，解释效果相同的原理)。然而更深的网络结构可以学习到更复杂的非线性关系，从而使模型的训练效果更好。该操作带来的另一个好处是减少参数数量，因为对于一个有C个卷积核的卷积层来说，原来的参数个数为7×7×C，而新的参数个数为3×(3×3×C)。

​

（1）对于表1的理解–以A网络为例：

进行第一组卷积操作时，输入是3×224×224，经过64个卷积核，经过2×2、步长为2的最大池化，分辨率减少一半，变成112×112；

进行第二组卷积操作，经过64×2=128个卷积核，经过池化之后，分辨率再减少一半，变成56×56；

第三组卷积操作，经过128×2=256个卷积核，经过池化之后，分辨率变为28×28；

第四组卷积操作，卷积核达到512，池化之后，得到分辨率为14×14的特征图；

第五组卷积操作，使用2个3×3的卷积核堆叠，再池化，分辨率变为7×7。

将7×7的特征图拉成一个向量，得到49×512个神经元（512个特征图），进入三个全连接层（神经元个数分别 4096 4096 100）

（2）A-E模型变换 演变过程：

A：11层卷积

A-LRN：第一组卷积操作结束的时候加了LRN

B：加深了网络模型，在第一组和第二组卷积操作中分别加一个3×3的卷积

C：在3.4.5组卷积的地方做了1×1卷积的尝试，（借鉴NIN，从激活函数考虑，1×1卷积就是做了一个线性变换），C增加了模型非线性的映射能力，精度有所提升。

D：vgg16，在C的基础上，把1×1卷积全部换成3×3卷积，可以获取更大的感受野，看看有没有更大的提升

E：vgg19，在3.4.5组卷积再增加一个3×3的卷积

（3）A-E的共性：

（1） 5个maxpool降低分辨率

（2） 池化后，特征图通道数要翻倍，直至512

（3） 3个FC层进行分类输出

（4） 池化之间采用多个卷积层堆叠，对特征进行提取和抽象

（4）A-E的对比:

A-B只针对1,2靠前的两组卷积操作增加卷积核，后面C-E只在后面三组增加卷积层。

是否越靠后的特征图 要利用的更多、抽象的 需要非线性更强的映射能力的卷积核操作 去完成？ 可能堆叠更多的卷积层，使用更多的非线性激活函数，非线性映射能力比较强。

1 参数量对比

虽然网络层增加了8层，但参数量并没有增加太多（优点）。

原因：AlexNet在全连接层占了一半的参数，所以增加小的3×3卷积层，参数不会增加太多的。

2 每组卷积操作中，卷积层堆叠的个数不同

二、分类框架（论文中的3）

①训练技巧（论文中的3.1 训练阶段）

设置S的两种方法：

固定值：256/384；

随机值：每个batch的S在[256,512]随机采样，实现尺度扰动

（1）数据增强——尺度扰动

针对位置/尺寸———尺寸扰动 scale jittering

训练阶段的尺寸扰动：按比例缩放图片至最小边为s；随机位置裁剪出224×224；随机进行水平翻转。

（2）预训练模型初始化 ：加速模型训练

利用浅层模型初始化深度的模型——BCDE使用A模型初始化

训练过程中尺度不同的时候，用小尺度上训练好的模型去初始化即将要训练的大尺度的模型——

S=384时，用S=256进行模型初始化；S=[256,512]时，用S=384模型初始化。

---

3.1第一段：

具体训练超参数的设置：batch size=256、momentum=0.9、L2=5*10^-4、学习率=0.01

学习率下降策略：每次下降×0.1，当验证集准确率不再上升的时候，就下降学习率。在pytorch中有对应的函数实现 reduce on Plateau

训练了74轮，迭代了370K次

3.1第二段：

网络初始化的设置：

深层网络初训练时，会用浅层网络的权重进行初始化。

先训练最浅的A模型。随机初始化。往后训练时，利用A模型前面的卷积层 以及相应的FC层 参数对应初始化到后面的模型。如果没有对应的层，就随机初始化。0均值，偏置=0。

Xavier初始化：直接全部采用Xavier，不要借鉴浅层的参数

3.1第三段：关于训练图片尺寸的设置：

（1) 超参数s：训练图片经过等比例缩放之后的最短边。卷积网络输入在缩放的图片上进行裁剪224×224。S不能小于224，不然图像会丢失。

(2) 设置S的两种方法：

固定值：256/384；

随机值：每个batch的S在[256,512]随机采样，实现尺度扰动

(3) 训练阶段的尺度扰动：

每个batch的s在[256,512]随机采样一个尺寸，按照s裁剪，实现尺度扰动;

多尺度multi-scale training用单尺度模型初始化.

---

②测试技巧——多尺度测试（论文中的3.2 测试阶段）

设置Q：

图片等比例缩放至最短边为Q

设置3个Q，对图片进行预测，取平均

1 当S为固定值时 Q=[S-32, S , S+32]

2 当S为随机值时，Q=(S_min，0.5*(S_min+S_max)， S_max）

（1）Dense稠密测试

将FC层转换为卷积操作，变为全卷积网络，实现任意尺寸图片输入。

1.FC层的权重数量是固定的，若训练和测试的size不一样，size不匹配的话会报错 。

CONV层，根据输入的大小在3个conv层进行计算，得到与输入数据相关的尺寸的feature map，再在h和w两个维度取平均，变成所要的1×1×1000

2.FC替换成CONV

​

（2）Multi-crop测试

step1 等比例缩放至三种尺寸Q1,Q2,Q3

step2

方法一 Dense 全卷积

方法二 multi-crop 多个位置裁剪224*224区域

方法三 multi-crop&Dense 综合取平均

Q：256,384,512
若Q=256，先截取224，256-224=32，还要截取4下，所以移动步长为32/4=8

---

3.2第一段：

稠密测试的过程，实现任意尺寸图片输入

图片等比例缩放至Q，Q可以≠S，将整张图片输入到模型中

稠密测试法：FC替换成1×1的卷积层，可以接受任意尺度的输入图片，输出特征图大小会根据输入的尺寸有所变化。

得到类分数特征图，进行平均池化，（与multi-crop得到的值做平均本质一样的，但稠密测试是整张图输入进去，可以高效地实现这个过程，避免了一系列的重复的卷积运算）

水平翻转的图片再进行一次稠密测试，之后再与原始图片的softmax的posteriors 取平均，得到最终值。

3.2第二段：

alexnet的tencrop有重复计算

multi-crop与dense互为补充

multi-crop：一张图片最终得到150张。

一个尺度用5×5的网格裁剪，得到25张图片，水平翻转后得到25×2=50张图片，有三个尺度，所以一共得到50×3=150张图片

---

三、实验结果及分析（论文中的4）

① single scale 单尺度（论文中4.1）

S为固定值时，Q=S，S为随机值时，Q=0.5（S_min+S_max）

​

1. 误差随深度加深而降低，当模型到达19层时，误差饱和不再下降；
2. 增加1×1有助于性能提升
3. 训练时加入尺度扰动，有助于性能提升

② multi-scale 多尺度（论文中4.2）

​

1. 测试时采用尺度扰动有助于性能提升

③ multi-crop 多次裁剪（论文中4.3）

​

 等步长的滑动224×224的窗口进行裁剪，1张图片得到150张图片输入到模型中。

1. multi-crop优于dense
2. multi-crop结合dense，可以形成互补，达到最优结果

互补：3.2中解释到，multi crop 卷积边界用padding是0去填充，缺少边界信息，Dense的边界有原始图片的信息

④ convnet fusion 模型融合（论文中4.4）

​

1. DE模型比较深，dense， multi crop 结合，得到最优结果。

⑤ comparison with the state of art 对比当前最优模型（论文中4.5）

​

1. 单模型时，vgg优于GoogleNet，并且vgg结构简单。

VGG总结：

• vgg-block内的卷积层都是同结构的，池化层都得上一层的卷积层特征缩减一半
• 深度较深，参数量够大，较小的filter size/kernel size

VGG16的keras实现

def VGG_16():   
    model = Sequential()
    
    model.add(Conv2D(64,(3,3),strides=(1,1),input_shape=(224,224,3),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(64,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(MaxPooling2D(pool_size=(2,2)))
    
    model.add(Conv2D(128,(3,2),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(128,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(MaxPooling2D(pool_size=(2,2)))
    
    model.add(Conv2D(256,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(256,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(256,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(MaxPooling2D(pool_size=(2,2)))
    
    model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(MaxPooling2D(pool_size=(2,2)))
    
    model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(Conv2D(512,(3,3),strides=(1,1),padding='same',activation='relu',kernel_initializer='uniform'))
    model.add(MaxPooling2D(pool_size=(2,2)))
    
    model.add(Flatten())
    model.add(Dense(4096,activation='relu'))
    model.add(Dropout(0.5))
    model.add(Dense(4096,activation='relu'))
    model.add(Dropout(0.5))
    model.add(Dense(1000,activation='softmax'))
    
    return model

VGG19另一种方法实现

from tensorflow import keras
import tensorflow as tf
 
class Vgg_block(keras.layers.Layer):
    def __init__(self,units,filters,**kwargs):
        super().__init__(**kwargs)
        self.main_layer = []
        for i in range(units):
            self.main_layer.append(keras.layers.Conv2D(filters=filters,kernel_size=(3,2),
                                                       padding="same",strides=(1,1),
                                                       activation="relu"))
        self.main_layer.append(keras.layers.MaxPool2D(pool_size=(2,2)))
    def call(self,inputs):
        Z = inputs
        for layer in self.main_layer:
            Z = layer(Z)
        return Z 
 
model = keras.models.Sequential()
model.add(keras.layers.Input(shape=(224,224,3)))
model.add(Vgg_block(2,64))
model.add(Vgg_block(2,128))
model.add(Vgg_block(4,256))
model.add(Vgg_block(4,512))
model.add(Vgg_block(4,512))
model.add(keras.layers.Flatten())
model.add(keras.layers.Dense(4096,activation="relu"))
model.add(keras.layers.Dropout(0.5))
model.add(keras.layers.Dense(4096,activation="relu"))
model.add(keras.layers.Dropout(0.5))
model.add(keras.layers.Dense(1000,activation="softmax"))

参考资料：

论文笔记：主干网络——VGG

卷积神经网络之VGG - 知乎

快速理解VGG网络

本论文系列主要介绍主干网络，后续会在此基础上更新其他部分网络，仅供个人学习参考！