用几何法推导三角形重心坐标

梯度

概念：梯度是个向量。方向表示坡度最大的方向，模长表示坡度。
符号：$\nabla$

一元函数的梯度：
$\nabla f(x)=f^{\prime }(x)$
这里梯度是一维向量，有两个方向，x正向和负向。模长(绝对值)表示曲线在x处的斜率。

二元函数的梯度：
$\nabla f(x,y)=\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)$
这里梯度是二维向量，有无数个方向，这个向量与OXY平面平行。模长表示曲面在(x,y,f(x,y))处最大的斜率。
说明：曲面在点(x,y,f(x,y))处，有无数条切线，每条切线都有自己的斜率，其中斜率最大值就是梯度的大小，斜率最大对应的切线在OXY平面的投影与梯度的方向平行。

示例如下图所示，曲面函数f(x,y)=x²+y²-1，点A(1,1,1)在曲面上，f(x,y)=0用黑色的圆表示：

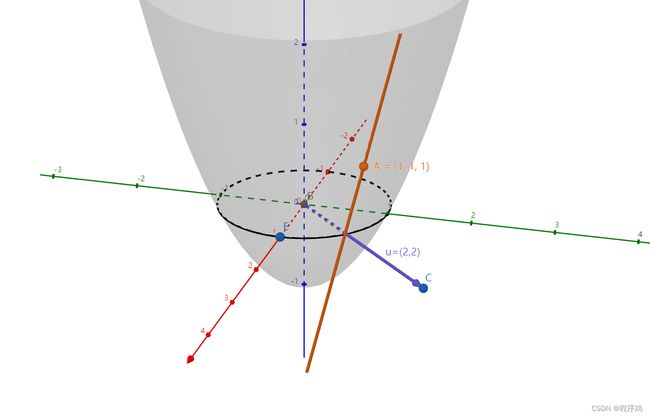
点A处的梯度为向量u=(2,2)，褐色直线是点A处斜率最大的切线，斜率最大值是向量u的模长$2\sqrt{2}$

过直线的平面的梯度与直线的关系

一种直线的形式：Ax+Bx+C=0
令f(x,y)=Ax+Bx+C，则该函数表示一个平面。

f(x,y)=x+y+1表示的平面如下图所示：

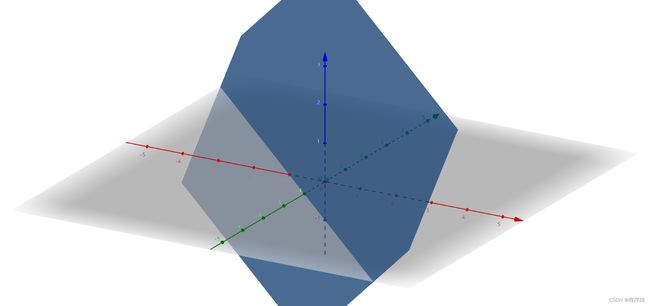
• 红色轴：X轴
• 绿色轴：Y轴
• 蓝色轴：Z轴
• 蓝色平面：f(x,y)=x+y+1
• 灰色平面：OXY平面
• 蓝色与灰色平面交线：f(x,y)=0，即x+y+1=0。

f(x,y)的梯度：对x y求偏导得(1,1)
由于梯度向量恒为(1,1)，所以在蓝色平面上的所有点处的梯度都一样。即平面上所有点处的最大坡度及指向最大坡度的方向都一样。

由于梯度向量一定是指向上坡方向的，那么梯度就与直线f(x,y)=0垂直。

综上，f(x,y)=Ax+Bx+C的梯度(A,B)，与直线f(x,y)=Ax+Bx+C=0垂直。

求直线的隐式方程

已知点M(x₀,y₀)，N(x₁,y₁)，如何求过两点的直线方程f(x,y)=Ax+By+C=0 ?

关键就是求得A B C三个系数的值

首先求A B的值，我们知道梯度向量n=(A,B)与直线垂直。设向量m=M-N，即m=(x₁-x₀,y₁-y₀)。
找一与向量m垂直的向量t (与n同向或反向)，则t=kn (k≠0)。
显然，向量t与向量m的点积为0，即t·m=t_xm_x+t_ym_y=0。可以令t_x=-m_y，t_y=m_x，这样就满足结果了。
求得：向量t=(y₀-y₁,x₁-x₀)

对于直线方程f(x,y)=Ax+By+C=0 ，两边同乘不为0的k得：kf(x,y)=kAx+kBy+kC=0。
由于t=kn，所以t=(kA,kB)。
求得：kA=(y₀-y₁)，kB=(x₁-x₀)

从而(y₀-y₁)x+(x₁-x₀)y+kC=0，将M点带入方程，(y₀-y₁)x₀+(x₁-x₀)y₀+kC=0。
求得：kC=x₀y₁-x₁y₀
尽管有可能kA≠A，kB≠B，kC≠C，但是kAx+kBy+kC=0与Ax+By+C=0表示的是同一条直线。

---

综上，直线方程为：(y₀-y₁)x+(x₁-x₀)y+x₀y₁-x₁y₀=0

有向距离

设f(x,y)=x+y+1，令f(x,y)=0, 1, 2, -1，这四条直线的图像如下：

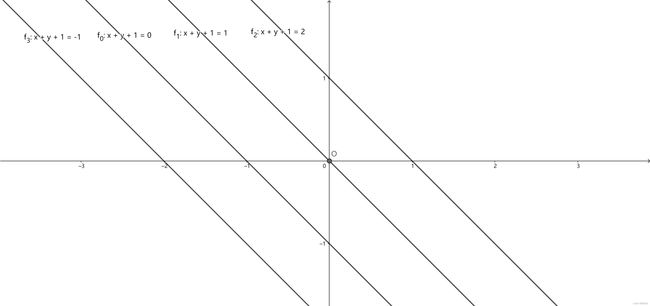
从图像中可以发现，四条直线是平行的。直线与直线之间的距离，与对应的f(x,y)的值有一定关系。

考虑值与距离的关系：

• a=f₁-f₀=1，b=f₂-f₀=2，c=f_.3-f₀=-1
• b=2a，f₂与f₀之间的距离是f₁与f₀之间距离的2倍，f₂与f₁位于f₀的同侧。
• c=-a，f₃与f₀之间的距离与f₁与f₀之间距离相同，但f₃与f₁位于f₀的异侧。

这里的a,b,c就是有向距离，有大小和方向。

已知任意点P，如何求点P到直线f(x,y)=0的距离?

看如下示例，点P=(x_p,y_p)，直线f(x,y)=x+y+1=0，过点P做直线的垂线交于点Q，向量u=P-Q，那么向量u的模长就是P到直线的距离。
我们知道梯度向量v=(1,1)与直线垂直，所以u=kv，|u|=|k||v|。

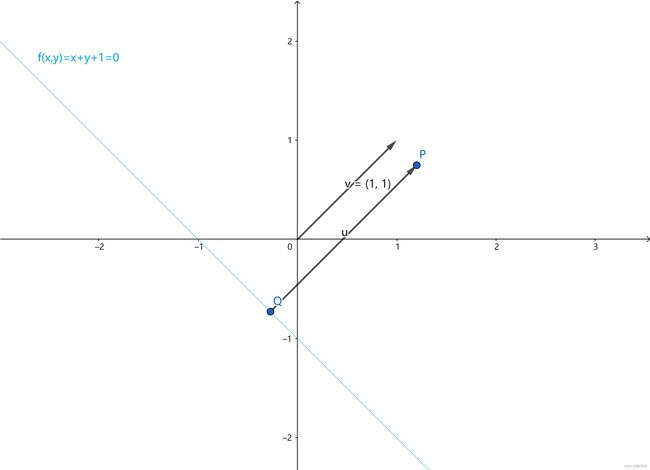
抽象之后，点P=(x_p,y_p)，点Q=(x_q,y_q)，直线f(x,y)=Ax+By+C，梯度向量v=(A,B)。
点到直线的有向距离（k无需取绝对值）$d=k\sqrt{A^2+B^2}$

显然，P=Q+u=Q+kv=(x_q+kA,y_q+kB)

求点P对应的f(x,y)的值：
f(x_p,y_p)=f(x_q+kA,y_q+kB)=A(x_q+kA)+B(y_q+kB)+C=Ax_q+By_q+C+kA²+kB²=kA²+kB²=k(A²+B²)
得：$k=\frac{f(x_q,y_q)}{A^2+B^2}$

综上，点P=(x_q,y_q)到直线f(x,y)=Ax+By+C=0的距离为：$d=\frac{f(x_q,y_q)}{\sqrt{A^2+B^2}}$

如果，我们知道两点M=(x₀,y₀)，N=(x₁,y₁)，那么就能写出任意点P(x,y)到点M，N所在直线的有向距离的函数d(x,y)：

$\begin{array}{r}d(x,y)=\frac{y_0-y_1}{\sqrt{{\left(x_1-x_0\right)}^2+{\left(y_0-y_1\right)}^2}}x+\frac{x_1-x_0}{\sqrt{{\left(x_1-x_0\right)}^2+{\left(y_0-y_1\right)}^2}}y+\frac{x_0{y}_1-x_1{y}_0}{\sqrt{{\left(x_1-x_0\right)}^2+{\left(y_0-y_1\right)}^2}}\end{array}$

重心坐标

何为重心坐标

直角坐标系

设点P的坐标为(2,3)，在平面直角坐标系下的P如下图所示：

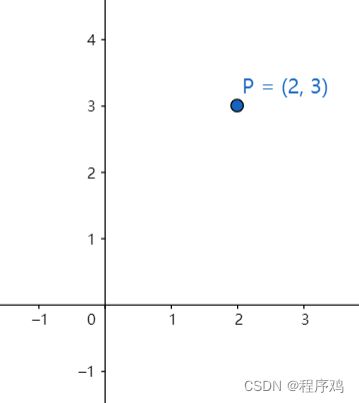
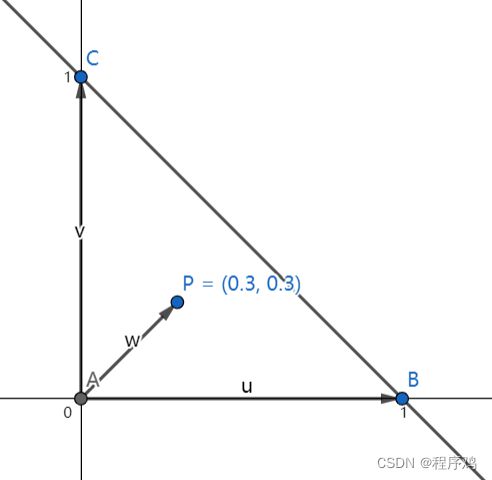
换另一个角度思考，设点O的坐标为(0,0)，向量u的坐标为(1,0)，向量v的坐标为(0,1)，向量w的坐标为(2,3)

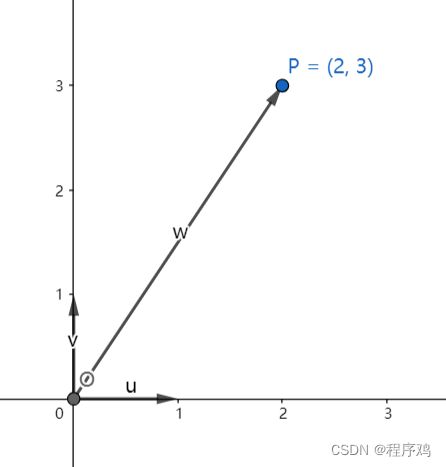
显然：w=2u+3v，P=O+w=O+2u+3v

在图上添加点B(1,0)，点C(0,1)，修改点O的标识为A

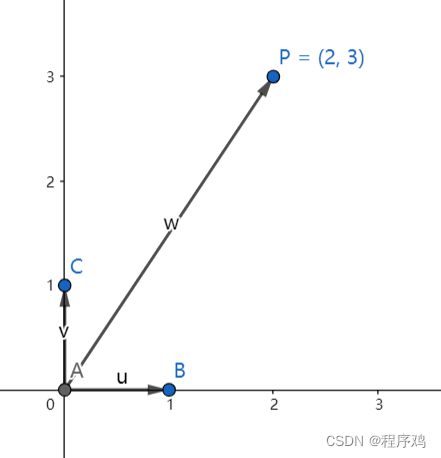
显然：u=B-A，v=C-A，则P=A+2(B-A)+3(C-A)=-4A+2B+3C
令α=-4，β=2，γ=3，则P=αA+βB+γC，且α+β+γ=1
注意：α+β+γ=1≡1

证明如下：
$P=A+m(B-A)+n(C-A)$
$P=(1-m-n)A+mB+nC$
$\alpha =1-m-n,\beta =m,\gamma =n$
$\therefore \alpha +\beta +\gamma =1$

我们可以使用三维坐标(α,β,γ)表示，这里的坐标就是关于三角形ABC的重心坐标。
在上面的这种特殊情况，β=x, γ=y，而α≡1-β-γ

---

非直角坐标系

非直角坐标系与直角坐标系类似：

• 直角坐标系：横轴是X轴，纵轴是Y轴，横轴与纵轴垂直，用(x,y)表示点的坐标
• 非直角坐标系：横轴是β轴，纵轴是γ轴，横轴与纵轴不垂直，用(β,γ)表示点的坐标

示例如下图：

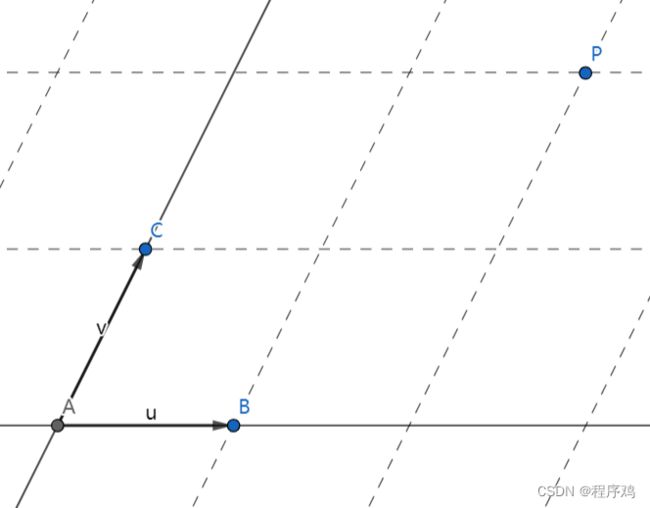
在图示的非直角坐标系下：
点A坐标(0,0)，点B坐标(1,0)，点C坐标(0,1)，点P坐标(2,2)
向量u=B-A，向量v=C-A
P=A+2u+2v=A+2(B-A)+2(C-A)=-3A+2B+2C
α=-3，β=2，γ=2

点P关于三角形ABC的重心坐标为(-3,2,2)

值得注意的是，虽然点P的坐标是(2,2)，但其关于三角形ABC的重心坐标却和ABC三个点息息相关

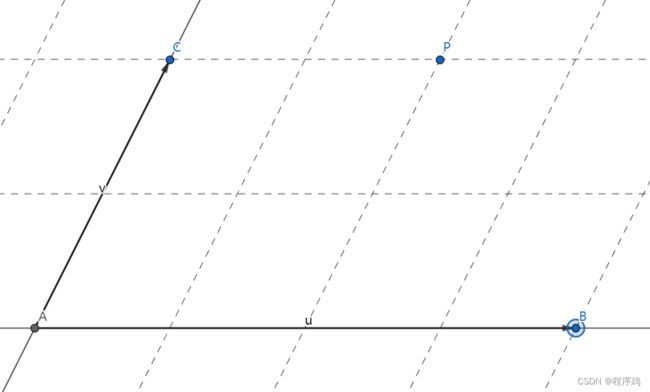
这里，点A坐标(0,0)，点B坐标(4,0)，点C坐标(0,2)
向量u=B-A，向量v=C-A
P=A+0.5u+v=A+0.5(B-A)+(C-A)=-0.5A+0.5B+C
α=-0.5，β=0.5，γ=1

点P关于三角形ABC的重心坐标为(-0.5,0.5,1)

已知直角坐标，求重心坐标

在直角坐标系下，点P(x_p,y_p)，点A(x_a,y_a)，点B(x_b,y_b)，点C(x_c,y_c)。
设f(x,y)=0为AC所在直线的方程，g(x,y)=0为AB所在直线的方程。

在非直角坐标系下，为了方便计算点P(β,γ)，我们规定点A(0,0)，点B(1,0)，点C(0,1)。

求β

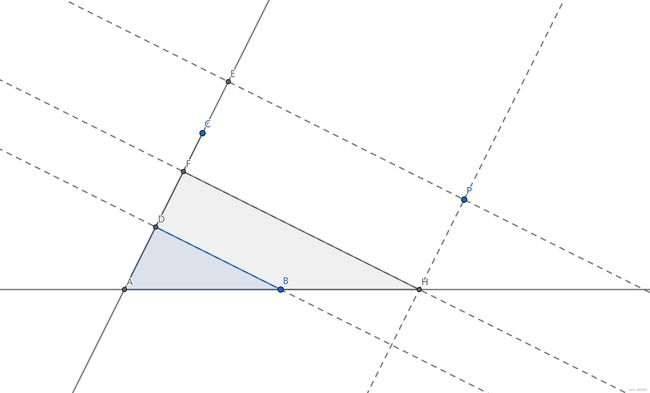
1. 过点B作AC所在直线的垂线于点D
2. 过点P作AC所在直线的垂线于点E
3. 过点P作AC所在直线的平行线L，L交AB所在直线于点H
4. 过点H作AC所在直线的垂线于点F

$显然PE=HF$

$\because △ABD\backsim △AHF$

$\therefore \frac{HF}{BD}=\frac{AH}{AB}$

$\because B=(1,0),A=(0,0)$

$\therefore AB=1,则\beta =AH=\frac{PE}{BD}$

$已知\frac{PE}{BD}=\frac{f\left(x_p,y_p\right)}{f\left(x_b,y_b\right)},且f(x,y)=\left(y_a-y_c\right)x+\left(x_c-x_a\right)y+x_a{y}_c-x_c{y}_a$

$\therefore \beta =\frac{\left(y_a-y_c\right)x_p+\left(x_p-x_a\right)y_p+x_a{y}_c-x_c{y}_a}{\left(y_a-y_c\right)x_b+\left(x_c-x_a\right)y_b+x_a{y}_c-x_c{y}_a}$

---

求γ

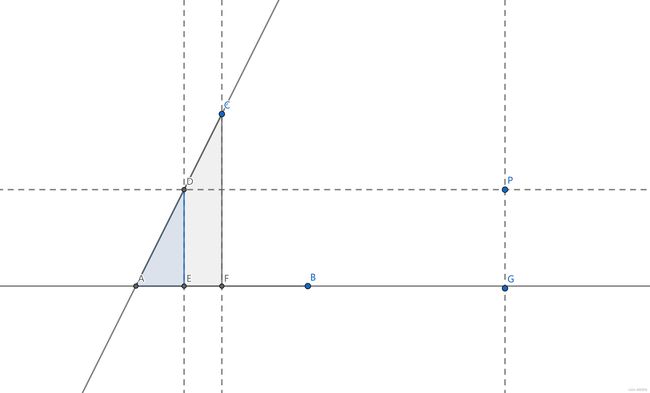
1. 过点C作AB所在直线的垂线于点F
2. 过点P作AB所在直线的垂线于点G
3. 过点P作AB所在直线的平行线L，L交AC所在直线于点D
4. 过点D作AB所在直线的垂线于点E

$显然PG=DE$

$\because △ADE\backsim △ACF$

$\therefore \frac{DE}{CF}=\frac{AD}{AC}$

$\because C=(0,1),A=(0,0)$

$\therefore AC=1,则\gamma =AD=\frac{PG}{CF}$

$已知\frac{PA}{CF}=\frac{g\left(x_p,y_p\right)}{g\left(x_c,y_c\right)},且g(x,y)=\left(y_a-y_b\right)x+\left(x_b-x_a\right)y+x_a{y}_b-x_b{y}_a$

$\therefore \gamma =\frac{\left(y_a-y_b\right)x_p+\left(x_b-x_a\right)y_p+x_a{y}_b-x_b{y}_a}{\left(y_a-y_b\right)x_c+\left(x_b-x_a\right)y_c+x_a{y}_b-x_b{y}_a}$

通过上面的讨论，直角坐标系P(x_p,y_p)，A(x_a,y_a)，B(x_b,y_b)，C(x_c,y_c)，非直角坐标系P的坐标：
$$P=(\beta ,\gamma )=(\frac{\left(y_a-y_c\right)x_p+\left(x_p-x_a\right)y_p+x_a{y}_c-x_c{y}_a}{\left(y_a-y_c\right)x_b+\left(x_c-x_a\right)y_b+x_a{y}_c-x_c{y}_a},\frac{\left(y_a-y_b\right)x_p+\left(x_b-x_a\right)y_p+x_a{y}_b-x_b{y}_a}{\left(y_a-y_b\right)x_c+\left(x_b-x_a\right)y_c+x_a{y}_b-x_b{y}_a})$$

直角坐标系P(x_p,y_p)，A(x_a,y_a)，B(x_b,y_b)，C(x_c,y_c)，点P关于三角形ABC的重心坐标：
$$P=(\alpha ,\beta ,\gamma )$$
$$\alpha =1-\beta -\gamma$$
$$\beta =\frac{\left(y_a-y_c\right)x_p+\left(x_p-x_a\right)y_p+x_a{y}_c-x_c{y}_a}{\left(y_a-y_c\right)x_b+\left(x_c-x_a\right)y_b+x_a{y}_c-x_c{y}_a}$$
$$\gamma =\frac{\left(y_a-y_b\right)x_p+\left(x_b-x_a\right)y_p+x_a{y}_b-x_b{y}_a}{\left(y_a-y_b\right)x_c+\left(x_b-x_a\right)y_c+x_a{y}_b-x_b{y}_a})$$

性质

在研究性质时，使用简单的例子观察较好，不仅简单，而且好发现规律。

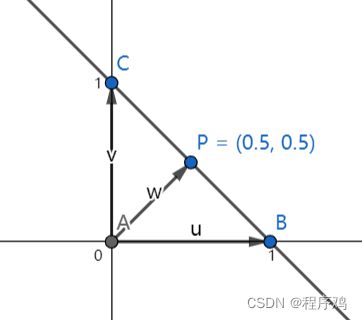
如图点P(0.5,0.5)，其β=0.5，γ=0.5，α=0。

先考虑三个特殊点ABC：

• 当点P位于点C时，β=0，γ=1，α=0；
• 同样当点P位于点B时β=1，γ=0，α=0；
• 当点P位于点A时β=0，γ=0，α=1。

再考虑三条边界线：

• 当点P位于线段BC上时，0≤β≤1，0≤γ≤1，且β+γ=1，则α=0。
• 当点P位于线段AC上时，β=0，0≤γ≤1，则α+γ=1，且0≤α≤1。
• 当点P位于线段AB上时，0≤β≤1，γ=0，则α+β=1，且0≤α≤1。

综上，当点P位于三角形ABC内部时，0<α<1，0<β<1，0<γ<1。
当点P位于三角形ABC的一条边上时，α,β,γ中有一个值为0，其他两个值位于0~1之间（闭区间）。
当点P位于三角形ABC的一个顶点时，α,β,γ中有两个值为0，剩余一个值为1。