[课程笔记](李沐-动手学深度学习)
文章目录
- 矩阵计算
-
- 标量导数
- 亚导数
- 梯度
- 自动求导
-
- 向量链式求导法则
- 自动求导
- 复杂度
- 自动求导实现
- softmax回归+损失函数
-
- softmax 回归
- 损失函数
- QA
- 权重衰退
- 丢弃法Dropout
-
- 从零开始实现dropout
- 数值稳定性 + 模型初始化和激活函数
-
- 数值稳定性——梯度消失和梯度爆炸
-
- 梯度爆炸
- 梯度消失
- 如何让训练更加稳定?
- 梯度消失和梯度爆炸的产生原因和解决办法?
- 模型初始化和激活函数
-
- 深度神经网络权值初始化的几种方式及为什么不能初始化为零
- Xavier Initialization
- Kaiming Initialization
- 多层感知机
-
- 感知机
- 多层感知机
- 激活函数
- 多类分类
- 从全连接到卷积
-
- 1*1卷积层
- 池化层
-
- 最大池化层
- 平均池化层
- LeNet
-
- 1. 手写数字识别
- 2. MNIST
- 3.LeNet的具体模型
- Alexnet
-
- 1. 历史
-
- 1.1 2000 流行的机器学习方法——SVM,核方法
- 1.2 2000计算机视觉主要方法——几何学
- 1.3 2010计算机视觉的热点问题——特征工程
- 1.4 硬件的发展奠定了深度学习的兴起
- 1.5 ImageNet(2010)
- 2. ALexnet架构
- 3.总结
- 使用块的网络 VGG
-
- 1. VGG块
- 2. VGG架构
- 3. 总结
- 4. 代码
- 5. QA
- 网络中的网络(NiN)
-
- 1. 动机
- 2. NiN块
- 3. NiN架构
- 4. NiN Networks
- 5. 总结
- 6.代码
- GoogLeNet /inceptionv1
-
- 含并行连结的网络(GoogLeNet)
- Inception块
- GoogLeNet模型
- 总结
- InceptionV2/V3
- Inception v4
- 稠密连接网络(DenseNet)
-
- 5.12.1 稠密块
- 5.12.2 过渡层
- DenseNet模型
- 小结
- BN批量归一化
-
- 训练深层网络时的问题
- 批量归一化
- 形式化表达
- 吴恩达老师深度学习课程中的批量归一化
- 从零实现BatchNorm
- CPU和GPU
-
- CPU
- GPU
- 单机多卡并行
- 多GPU训练实现
- 分布式训练
-
- 分布式计算
- GPU机器架构
- 关于性能
- 数据增广
- 微调
- 样式迁移
- 序列模型
-
- 序列数据及其统计工具
- 马尔科夫假设
- 潜变量模型
- 马尔科夫假设MLP模型训练
- QA
- RNN循环神经网络
-
- 梯度裁剪
- 更多的RNNs
- 门控循环单元GRU
-
- 1. 动机:如何关注一个序列
- 2. 门的概念
- 3. 候选隐状态
- 4. 真正的隐状态
- 5. 总结
- 6. QA
- 长短期记忆网络(LSTM)
-
- 1.长短期记忆网络:
-
- 1.1 门
- 1.2 候选记忆单元
- 1.3 记忆单元
- 1.4 隐状态
- 深度循环神经网络
-
- 双向循环神经网络
- 双向循环神经网络的错误应用
- 编码器解码器结构
- Seq2Seq
- 注意力机制
- 注意力分数
-
- 掩蔽softmax操作
- 可加性注意力
- 缩放的“点-积”注意力
- 使用注意力机制的seq2seq
- 自注意力和位置编码
-
- 自注意力
- 位置编码
- Transformer
-
- 1.transformer架构
- 2.多头注意力
- 3.有掩码的多头注意力
- 4.基于位置的前馈网络
- 5.层归一化
- 6.信息传递
- 7.预测
- 总结
- QA
- BERT
- 优化算法
矩阵计算
标量导数
![]()
亚导数
梯度
将导数拓展到向量->梯度
![]()
第一种情况:y标量x向量
- 标量关于列向量的导数是一个行向量
- 梯度和等高线是正交的,意味着是梯度指向的是你的值变化最大的地方
补充:内积
![]()
可以这样来理解向量内积:
向量a、b的内积等于向量a在b方向的分量(或投影)与b的内积,当a、b垂直时,a在b方向上无分量,所以内积为0。
其他几何意义:从内积数值上我们可以看出两个向量的在方向上的接近程度。
当内积值为正值时,两个向量大致指向相同的方向(方向夹角小于90度);
当内积值为负值时,两个向量大致指向相反的方向(方向角大于90度);
当内积值为0时,两个向量互相垂直
第二种情况:x标量y向量
_第4张图片](http://img.e-com-net.com/image/info8/390e1c3089ad44fe990c2c3a971ddf8a.jpg)
第二种情况:x向量y向量
自动求导
向量链式求导法则
自动求导
显示构造就是数学上的那种
复杂度
假设神经网络有n层(n个操作子)
内存:神经网络耗费GPU资源的最大原因
_第16张图片](http://img.e-com-net.com/image/info8/b5a067ba7fbc4e799d1dc34ee6ec8016.jpg)
自动求导实现
![]()
loss通常是一个标量,向量对于一个矩阵的loss就会变成矩阵,矩阵再往下走就变成一个4维矩阵,神经网络一深就变成一个特别大的张量
![]()
是的
softmax回归+损失函数
softmax 回归
_第24张图片](http://img.e-com-net.com/image/info8/7f5d265bca7542c5bee156fff14836e2.jpg)
_第25张图片](http://img.e-com-net.com/image/info8/d3aca5aa4d63437390a7f95862cfd51f.jpg)
可以看到,对于分类问题来讲,我们不关心对于非正确类的预测值,我们只关心正确类的置信度有多大
_第26张图片](http://img.e-com-net.com/image/info8/cd7a9ff62af148a2b42e34fbcca2a1c8.jpg)
损失函数
L1损失函数的导数是说,不管我的预测值和真实值离得多远权重更新也不会特别大,带来稳定性上的好处。但是0点处-1到1之间的剧烈变化,这个不平滑性导致当预测值靠得近的时候,也就是优化到末期的时候这个地方就不那么稳定了
QA

onehot正确为1剩余为0,用softmax逼近纯0-1的分布,问题是很难用指数逼近1,因为指数变成1要求输出几乎接近于无穷大,所以用softlabel(0.1-0.9)真的用softmax去拟合那些0.9是可能的
权重衰退
怎么控制一个模型的容量?一个是我把模型控制的比较小,参数比较少,第二个是使得每个参数的值的范围比较小,权重衰退就是通过控制整个值的选择范围来进行的
_第32张图片](http://img.e-com-net.com/image/info8/ef488ee6447b46e5bf0a41cb07e6bbc8.jpg)
_第33张图片](http://img.e-com-net.com/image/info8/5f74a1a487424fd4a54ddd720e2374c5.jpg)
惩罚项的引入使得我的最优解往原点走了,最优解的值变小,模型的复杂度变低了
正则化如何让权重衰退?
![]()
因为lamda的引入,每次更新前我们先把我们的权重做了一次放小
![]()
_第34张图片](http://img.e-com-net.com/image/info8/724d3416c2f047669bdf8b85593665f9.jpg)
_第35张图片](http://img.e-com-net.com/image/info8/e0d8a4bdf0ca4c1e82004eea01c9eafd.jpg)
因为数据有噪音,你学到的参数可能特别大,因为我们的算法看到的是噪音,只要模型允许的话他不断试图去选一个权重记住我所有的样本,那就会尝试记住噪音,记住那些抖动的东西,他就会学到一个特别大的地方
丢弃法Dropout
- 正则就是防止你的权重比较大,是一个避免过拟合的方法
- 在数据里面加入噪音等价于一个正则,之前在数据里加噪音,这里是一个随机加噪音
- 丢弃法Dropout是在输入加噪音,在层也加噪音
_第38张图片](http://img.e-com-net.com/image/info8/f59c0bbe642e4c4ebf236e981194948e.jpg)
_第39张图片](http://img.e-com-net.com/image/info8/e2009806a22743278de9dd8913b8cd85.jpg)
保证均值/期望不会变
_第40张图片](http://img.e-com-net.com/image/info8/07d73cf19a104fe797297c4f3d430c5a.jpg)
_第41张图片](http://img.e-com-net.com/image/info8/96ba982f7d83422a880acf27d57a59ed.jpg)
dropout只会对你的权重产生影响,在预测的时候权重都不需要发生变化的时候我们是不需要正则的
_第42张图片](http://img.e-com-net.com/image/info8/869d9561f0ed4f5cb3d838ef50dcb774.jpg)
没有理论依据,实验效果上和正则(主流)一样
_第43张图片](http://img.e-com-net.com/image/info8/ca885975f87b4fab8aa18015a4fba375.jpg)
从零开始实现dropout
import torch
from torch import nn
from d2l import torch as d2l
import torchvision
from torchvision import transforms
from torch.utils import data
def dropout_layer(X,dropout):
assert 0<=dropout <= 1
# 如果dropout概设置为1,全部元素被丢弃
if dropout == 1:
return torch.zeros_like(X)
# 如果dropout概设置为0,全部元素被保留
if dropout == 0:
return X
mask = (torch.rand(X.shape)>dropout).float() #使用mask而不是直接置零是为了提高计算效率
return mask *X/(1.0-dropout)
# 测试dropout layer层
X = torch.arange(16,dtype=torch.float32).reshape((2,8))
print(X)
print(dropout_layer(X,0))
print(dropout_layer(X,0.5))
print(dropout_layer(X,1))
测试Dropout的结果:
数值稳定性 + 模型初始化和激活函数
数值稳定性——梯度消失和梯度爆炸
_第45张图片](http://img.e-com-net.com/image/info8/bfd4318bdd4b453e8bf51e06d9c88230.jpg)
注:1. y在这里不是预测,还包括了损失函数
2. 这里的h都是向量,向量关于向量的导数是矩阵,是矩阵乘法,所以我们的主要问题也是来自这个地方,因为我们做了太多的矩阵乘法
_第46张图片](http://img.e-com-net.com/image/info8/e1d7e040c2d647e1ae0acd749ba2adf0.jpg)
![]()
delta是一个按元素的函数,所以他的求导就变成一个对角矩阵
梯度爆炸
_第47张图片](http://img.e-com-net.com/image/info8/ba785be108c4482f9b660524ea46b1a9.jpg)
relu作为激活函数求导,相当于吧某一列留住了或者变为0;假设w_i的值非常大(大于1)的话,那么最后会有非常大的值,发生梯度爆炸
_第48张图片](http://img.e-com-net.com/image/info8/1d4f4d02250a4318bfd157c1d485d39c.jpg)
3. 学习率太大,因为我们一步走的比较远,对权重的更新权重变得比较大,我们的梯度就是权重的乘法,更大的梯度,那就会带来更大的参数值。。。
4. 也不算是完全没法训练,就是调学习率变得很难调,学习率只有一个很小的范围内是好的
梯度消失
_第49张图片](http://img.e-com-net.com/image/info8/d0159e6794714bf59eb8a2b8f42dcf9e.jpg)
![]()
![]()
_第50张图片](http://img.e-com-net.com/image/info8/b052658c51424a01980d881c4130fb1f.jpg)
你的梯度其实就是对n个层做累乘,如果你的值比较小或者激活函数使得你的值变得比较小。。。
如何让训练更加稳定?
_第51张图片](http://img.e-com-net.com/image/info8/225574e7b9be4533bdd5ecd3fb6238aa.jpg)
如果你的时序序列很长的话,比如是100,输入一个时序为100的句子,
原始的RNN就是对这100个时序做乘法。LSTM吧这些乘法变成加法,吧100次乘法变成100次加法
梯度消失和梯度爆炸的产生原因和解决办法?
什么是梯度消失和梯度爆炸
在反向传播过程中需要对激活函数进行求导,如果导数大于1,那么随着网络层数的增加梯度更新将会朝着指数爆炸的方式增加这就是梯度爆炸。同样如果导数小于1,那么随着网络层数的增加梯度更新信息会朝着指数衰减的方式减少这就是梯度消失。因此,梯度消失、爆炸,其根本原因在于反向传播训练法则,属于先天不足。
梯度消失、爆炸导致原因
- 从BP(反向传播原理)解释梯度消失和梯度爆炸
- 从激活函数角度分析梯度消失
如果激活函数选择不合适,比如使用sigmoid,梯度消失就会很明显了,原因看下图,左图是sigmoid的损失函数图,右边是其导数的图像,如果使用sigmoid作为损失函数,其梯度是不可能超过0.25的,这样经过链式求导之后,很容易发生梯度消失,sigmoid函数数学表达式为:
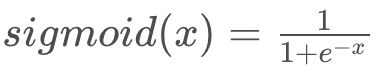
_第52张图片](http://img.e-com-net.com/image/info8/4d73c65bbe7d4d899c247e96b186ee5c.jpg)
同理,tanh作为激活函数,它的导数图如下,可以看出,tanh比sigmoid要好一些,但是它的导数仍然是小于1的。tanh数学表达为:
梯度消失、爆炸的解决方案
- 预训练加微调
为了解决梯度的问题,采取无监督逐层训练方法,其基本思想是每次训练一层隐节点,训练时将上一层隐节点的输出作为输入,而本层隐节点的输出作为下一层隐节点的输入,此过程是逐层“预训练”(pre-training);在预训练完成后,再对整个网络进行“微调”(fine-tunning)。此思想相当于是先寻找局部最优,然后整合起来寻找全局最优,此方法有一定的好处,但是目前应用的不是很多了。 - 梯度剪切及正则化解决梯度爆炸
梯度剪切这个方案主要是针对梯度爆炸提出的,其思想是设置一个梯度剪切阈值,然后更新梯度的时候,如果梯度超过这个阈值,那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。
另外一种解决梯度爆炸的手段是采用权重正则化(weithts regularization)。
正则化是通过对网络权重做正则限制过拟合,仔细看正则项在损失函数的形式:
![]()
其中, alpha是指正则项系数,因此,如果发生梯度爆炸,权值的范数就会变的非常大,通过正则化项,可以部分限制梯度爆炸的发生。但在深度模型中,梯度消失更常见一些。
-
batch normalization
Batchnorm是深度学习发展以来提出的最重要的成果之一了,目前已经被广泛的应用到了各大网络中,具有加速网络收敛速度,提升训练稳定性的效果,Batchnorm本质上是解决反向传播过程中的梯度问题。batchnorm全名是batch normalization,简称BN,即批规范化,通过规范化操作将输出信号x规范化到均值为0,方差为1保证网络的稳定性。
batchnorm就是通过对每一层的输出规范为均值和方差一致的方法,消除了x带来的放大缩小的影响,进而解决梯度消失和爆炸的问题。 -
残差学习和LSTM
模型初始化和激活函数
_第54张图片](http://img.e-com-net.com/image/info8/fc7712a38044460295222a8933bbcefa.jpg)
不管你的网络有多深,最后一层和第一层都差不多,都是均值为0方差为某个特定值,我希望我的输出和梯度都在这个区间里面
-
因为在训练开始的时候更容易有数值不稳定,;比如初始的时候梯度比较大,可能W变得更加大,然后出问题
-
随机初始化参数有什么问题?
随机初始化没有控制方差,所以对于深层网络而言,随机初始化方法依然可能失效。
理想的参数初始化还得控制方差,对w进行一个规范化
_第56张图片](http://img.e-com-net.com/image/info8/e6b1b2ced0324d1b83e4c8d5ba17b5e1.jpg)
_第57张图片](http://img.e-com-net.com/image/info8/fa995e2fddd140c0829ec040fe4a397f.jpg)
_第58张图片](http://img.e-com-net.com/image/info8/1d8284ca3ed3402ba937183c511d3737.jpg)
_第59张图片](http://img.e-com-net.com/image/info8/6ed80c49892146549333f7fb62e9e0b7.jpg)
nt-1是输入的维度,nt是输出的维度,除非输入刚好等于输出,否则无法同时满足这两个条件
_第60张图片](http://img.e-com-net.com/image/info8/c70485dca3284dd5abbd8fa9f3a1dd09.jpg)
为了使得我的前向输出都是均值为0方差为1,激活函数必须等于本身
![]()
反向也一样
_第61张图片](http://img.e-com-net.com/image/info8/c13be880606f4b389cb59a3af7c6e8f5.jpg)
_第62张图片](http://img.e-com-net.com/image/info8/efcff03da2214fe3b08f0a777e5092f8.jpg)
具体来说,我们每一层的输出和每一层的梯度都是均值为0方差为固定数的随机变量,权重初始化选用Xavier,激活函数选用relu或者tanh都没有太大问题,sigmoid可以做一下变换
![]()
- inf就是太大了,一般都是学习率太大或者权重初始的值太大了
- NaN一般就是一个数除以0了
- 解决的话就是合理的初始化权重,激活函数不要选错,学习率不要太大。如果碰到这个问题,最简单的做法就是吧学习率调到比较小,直到inf或者NAN不再出现,第二就是看一下权重的初始,方差小一点
_第63张图片](http://img.e-com-net.com/image/info8/baa9292c9bf847b9b5eb79333cadd30b.jpg)

是的,一般NAN就是梯度太大造成的,如果太小就不会有什么进展train不动
![]()
深度神经网络权值初始化的几种方式及为什么不能初始化为零
深度神经网络权值初始化的几种方式及为什么不能初始化为零
在深度学习中,神经网络的权重初始化方式非常重要,其对模型的收敛速度和性能有着较大的影响。一个好的权值初始值有以下优点:
· 梯度下降的收敛速度较快
· 深度神经中的网络模型不易陷入梯度消失或梯度爆炸问题
0 初始化
在线性回归和逻辑回归中,我们通常把权值 w 和偏差项 b 初始化为0,并且我们的模型也能取得较好的效果。在线性回归和逻辑回归中,我们采用类似下面的代码将权值初始化为0(tensorflow框架下):
w = tf.Variable([[0,0,0]],dtype=tf.float32,name='weights')
b = tf.Variable(0,dtype=tf.float32,name='bias')
但是,当在神经网络中的权值全部都使用 0 初始化时,模型无法正常工作了。
原因是:在神经网络中因为存在隐含层。我们假设模型的输入为[x1,x2,x3],隐含层数为1,隐含层单元数为2,输出为 y
z1 = w10 * x0 + w11 * x1 + w12 * x2 +w13 * x3
z2 = w20 * x0 + w21 * x1 + w22 * x2 +w23 * x3
在所有的权值 w 和偏差值 b (可以看做是w10)初始化为 0 的情况下,即计算之后的:
z1 = 0,z2 = 0
那么由于
a1 = g(z1) 、a2 = g(z2)
经过激活函数之后得到的 a1 和 a2 也肯定是相同的数了
即 a1 = a2 = g(z1)
则输出层:y = g(w20 * a0 + w21 * a1 + w22 *a2 )
也是固定值了。
重点:在反向传播过程中,我们使用梯度下降的方式来降低损失函数,但在更新权值的过程中,代价函数对不同权值参数的偏导数相同 ,即 Δw 相同,因此在反向传播更新参数时:
w21 = 0 + Δw
w22 = 0 + Δw
实际上使得更新之后的不同节点的参数相同,同理可以得到其他更新之后的参数也都是相同的,不管进行多少轮的正向传播和反向传播,得到的参数都一样!因此,神经网络就失去了其特征学习的能力。
总结一下:在神经网络中,如果将权值初始化为 0 ,或者其他统一的常量,会导致后面的激活单元具有相同的值,所有的单元相同意味着它们都在计算同一特征,网络变得跟只有一个隐含层节点一样,这使得神经网络失去了学习不同特征的能力!
Xavier Initialization
Xavier Initialization
早期的参数初始化方法普遍是将数据和参数normalize为高斯分布(均值0方差1),但随着神经网络深度的增加,这方法并不能解决梯度消失问题。
_第65张图片](http://img.e-com-net.com/image/info8/b1cc5e9b28ec426c9d3695aa29248581.jpg)
Xavier初始化的作者,Xavier Glorot,在Understanding the difficulty of training deep feedforward neural networks论文中提出一个洞见:激活值的方差是逐层递减的,这导致反向传播中的梯度也逐层递减。要解决梯度消失,就要避免激活值方差的衰减,最理想的情况是,每层的输出值(激活值)保持高斯分布。
为什么我们首先需要初始化?
_第66张图片](http://img.e-com-net.com/image/info8/ee89516195c841e199bb19a041e56507.jpg)
Xavier 初始化到底是什么?
在我们开始训练之前分配网络权重似乎是一个随机的过程,对吧?我们对数据一无所知,因此我们不确定如何分配在该特定情况下有效的权重。一个好方法是从高斯分布中分配权重。显然,这种分布的均值为零,并且具有一些有限方差。让我们考虑一个线性神经元:
![]()
对于每个传递层,我们希望方差保持不变。这有助于我们防止信号爆炸到高值或消失到零。换句话说,我们需要以这样的方式初始化权重,即 x 和 y 的方差保持不变。此初始化过程称为 Xavier 初始化。
如何执行 Xavier 初始化?
Kaiming Initialization
我们提到Xavier初始化方法适用的激活函数有限:关于0对称;线性。而ReLU激活函数并不满足这些条件,实验也可以验证Xavier初始化确实不适用于ReLU激活函数。
![]()
Xavier初始化在Relu层表现不好,主要原因是relu层会将负数映射到0,影响整体方差。所以何恺明在对此做了改进提出Kaiming初始化,一开始主要应用于计算机视觉、卷积网络。
在ReLU网络中,假定每一层有一半的神经元被激活,另一半为0,所以,要保持方差不变,只需要在 Xavier 的基础上再除以2
也就是说在方差推到过程中,式子左侧除以2.
在Xavier论文中,作者给出的Glorot条件是:正向传播时,激活值的方差保持不变;反向传播时,关于状态值的梯度的方差保持不变。这在本文中稍作变换:正向传播时,状态值的方差保持不变;反向传播时,关于激活值的梯度的方差保持不变。
其中,激活值是激活函数输出的值,状态值是输入激活函数的值。
多层感知机
感知机
从现在的观点来看,感知机实际上就是神经网络中的一个神经单元
- w与x算内积
- 感知机其实就是一个二分类的问题(1,0问题当然也可以当成1,-1分类)
_第69张图片](http://img.e-com-net.com/image/info8/4e7896397f1b4444b5d00e056f158660.jpg)
感知机能解决二分类问题,但与线性回归和softmax回归有所区别:线性回归与softmax回归的输出均为实数,softmax回归的输出同时还满足概率公理。

_第70张图片](http://img.e-com-net.com/image/info8/68319927e0f0403396da7baec6428337.jpg)
线性模型的缺陷
猫狗分类的例子:
- 感知机是一个二分类模型,是最早的AI模型之一。
- 它的求解算法等价于使用批量大小为1的梯度下降。
- 它不能拟合XOR函数,这导致了第一次AI寒冬。
多层感知机
我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制, 使其能处理更普遍的函数关系类型。 要做到这一点,最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到上面的层,直到生成最后的输出。 我们可以把前 L−1 层看作表示,把最后一层看作线性预测器。 这种架构通常称为多层感知机(multilayer perceptron),通常缩写为MLP。
怎么解决XOR问题?
- 线性模型肯定是不行,我们可以分为几步来完成:第一步学出来蓝色的线,然后再学习一根黄色的线。有了蓝色和黄色分类器的结果,我们看两个结果是不是一样(正正得正),然后进入灰色分类器得到正确结果。
- 仍以XOR问题为例,XOR问题的一个解决思路是分类两次,先按x轴分类为+和-,再按y轴分类为+和-,最后将两个分类结果相乘,+即为一三象限,-即为二四象限:
- 蓝 黄-》灰
- 这实际上将信息进行了多层次的传递:
_第73张图片](http://img.e-com-net.com/image/info8/170ab40b38ef48e9a9c3467a292cbfea.jpg)
有了XOR问题的解决经验,可以想到如果将多个感知机堆叠起来,形成具有多个层次的结构,如图:
_第74张图片](http://img.e-com-net.com/image/info8/43d91d296c494a9cb3a0ad89c96c4eea.jpg)
这里的模型称为多层感知机,第一层圆圈称为输入x1 x2 x3 x4 x5(实际上他并非感知机),之后的一层称为隐藏层,由5个感知机构成,他们均以前一层的信息作为输入,最后是输出层,以前一层隐藏层的结果作为输入。除了输入的信息和最后一层的感知机以外,其余的层均称为隐藏层,隐藏层的设置为模型一个重要的超参数,这里的模型有一个隐藏层。
_第75张图片](http://img.e-com-net.com/image/info8/73792d6dc3044f55affb2aa95186a155.jpg)
为什么需要激活函数?
- 假设没有激活函数的话,输出仍然是线性函数,多层感知机仍然是单层感知机
- 但是仅仅有线性变换是不够的,如果我们简单的将多个线性变换按层次叠加,由于线性变换的结果仍为线性变换,所以最终的结果等价于线性变换,与单个感知机并无区别,反而加大了模型,浪费了资源,为了防止这个问题,需要对每个单元(感知机)的输出通过激活函数进行处理再交由下一层的感知机进行运算,这些激活函数就是解决非线性问题的关键。
_第76张图片](http://img.e-com-net.com/image/info8/090faf0df81c416fbb43cba6635c1559.jpg)
激活函数
激活函数(activation function)通过计算加权和并加上偏置来确定神经元是否应该被激活,它们将输入信号转换为输出的可微运算。大多数激活函数都是非线性的。
_第77张图片](http://img.e-com-net.com/image/info8/8c18910e46af4bc4b932daf51145e4dd.jpg)
_第78张图片](http://img.e-com-net.com/image/info8/dc9357aaebf84c86affe089170990d7d.jpg)
指数运算在CPU上是很贵的,sigmoid和tanh都有指数运算(可能相当于一百次乘法运算的时间),GPU上好一点但还是很贵,而relu没有
_第79张图片](http://img.e-com-net.com/image/info8/89a8e19f789d473cb9519df93d06870d.jpg)
多类分类
_第81张图片](http://img.e-com-net.com/image/info8/13505952c35549859aaa989b7e5a6284.jpg)
隐藏层先压缩再扩展可能会损失一些信息,再恢复就比较难了。卷积的话先压缩再扩展可以防止模型过拟合
_第82张图片](http://img.e-com-net.com/image/info8/1151813f1e974e209f470b367b5295dc.jpg)
从全连接到卷积
![]()
参数共享和局部连接
卷积是一个特殊的(受限)的全连接层。
1*1卷积层
池化层
检测边缘,假设卷积核[1,-1],
_第88张图片](http://img.e-com-net.com/image/info8/9ae8b444b0484607aa6c6db8863ab422.jpg)
我们需要一定的平移不变性,物体稍微的改动不会太影响输出
卷积对位置太敏感不是一个太好的事情,所以需要池化层
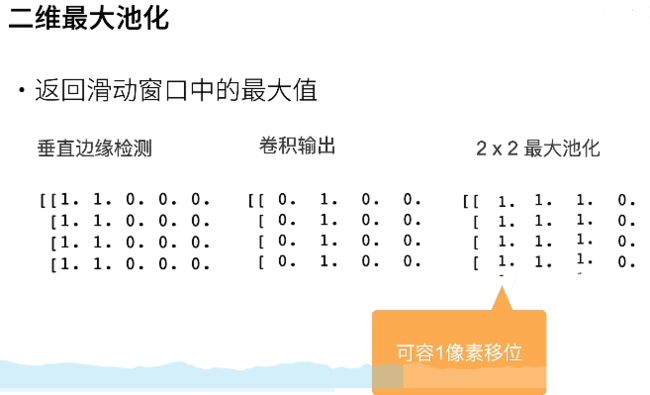
最大池化层
- 二维最大池化允许你的输入发生一定小小的偏移,使得你的卷积输出有一点模糊化 的效果,使得在输出的值的附近的一个小窗口里面值都会出现
- 有跟卷积类似的超参数:填充和步幅,但是没有可学习参数
- 不像卷积一样融合多输入通道,池化对每个通道做一次池化层

平均池化层
_第89张图片](http://img.e-com-net.com/image/info8/efb0003e76554794b903c0f151cc22a7.jpg)
_第90张图片](http://img.e-com-net.com/image/info8/bf362992489d41ceb2d10846682fb5d0.jpg)
池化层对特征图进行压缩。1.使特征图变小,简化网络计算复杂度,减少下一层的参数和计算量,防止过拟合;2.进行特征压缩,提取特征,保留主要的特征;保持某种不变性,包括平移、(旋转?)和尺度,尺度不变性也就是增大了感受野。
缺点:但是它在降维的过程中丢失了一些信息(因为毕竟它变小了嘛,只留下了它认为重要的信息),降低了分辨率。
卷积的stride也可以使得特征图变小
另外,现在的数据增广操作一定程度上已经从数据层面上使得你的卷积不会过拟合到某一个位置,这就淡化了池化层的作用
参考
LeNet
1. 手写数字识别
- LeNet网络最早是为了应用于手写数字的识别应用。
- 应用背景:
邮政局希望可以自动读出信件上的邮政编码
人们希望可以用支票自动取钱 - 该模型在80年代末的银行被真正的部署
2. MNIST
3.LeNet的具体模型
- LeNet-5是一个较简单的卷积神经网络。下图显示了其结构:输入的二维图像,先经过两次卷积层到池化层,再经过全连接层,最后使用softmax分类作为输出层
- LeNet-5 这个网络虽然很小,但是它包含了深度学习的基本模块:卷积层,池化层,全连接层。是其他深度学习模型的基础
总结
- LeNet-5是一种用于手写体字符识别的非常高效的卷积神经网络。
- 卷积神经网络能够很好的利用图像的结构信息。
- 卷积层的参数较少,这也是由卷积层的主要特性即局部连接和共享权重所决定。
Alexnet
1. 历史
1.1 2000 流行的机器学习方法——SVM,核方法
-
核方法替代了之前的神经网络网络方法,SVM对于调参不敏感,现在也有一些应用
-
本质上是特征提取,具体的方法是选择核函数来计算,把特征映射到高纬空间,使得他们线性可分
-
经过核函数计算之后,原问题可以转化为凸优化问题,这是2006年左右的研究热点
-
核方法有很多漂亮的定理,有很好的数学解释性
-
2010年左右,深度学习才兴起
1.2 2000计算机视觉主要方法——几何学
- 首先还是对图片进行特征抽取
- 希望把计算机视觉问题描述成几何问题,建立(非)凸优化模型,可以得到很多漂亮的定理。
- 可以假设这是一个几何问题,假设这个假设被满足了,可以推出很好的效果
1.3 2010计算机视觉的热点问题——特征工程
1.4 硬件的发展奠定了深度学习的兴起
1.5 ImageNet(2010)
-
AlexNet赢得了2012年ImageNet竞赛冠军
-
本质上是一个加强版的LeNet,更深更大
-
AlexNet主要改进措施:
1 dropout和数据增强(正则)
2 ReLu(梯度更大)
3 MaxPooling(取最大值,梯度相对增大) -
影响:计算机视觉方法论的改变,从人工提取特征过渡到CNN学习特征
包含许多特征的深度模型需要大量的有标签数据,才能显著优于基于凸优化的传统方法(如线性方法和核方法)。
-
relu替换sigmoid,relu的梯度确实是更大,relu在0点处的一阶导数确实是更好一点,他能够支撑更深的模型
-
lenet大家还是认为是一个机器学习的模型,ALexnet增大了几十倍,量变引起质变,他对整个计算机视觉的改变是观念上的改变。深度神经网络之前是进行人工特征提取然后用一个标准的机器学习模型比如SVM,我觉得SVM要什么特征比较好,但深度学习分类器和特征提取器是一起训练的过程
2. ALexnet架构
net = nn.Sequential(
这里,我们使用一个11*11的更大窗口来捕捉对象。
# 同时,步幅为4,以减少输出的高度和宽度。
# 另外,输出通道的数目远大于LeNet
nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
# 减小卷积窗口,使用填充为2来使得输入与输出的高和宽一致,且增大输出通道数
nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
# 使用三个连续的卷积层和较小的卷积窗口。
# 除了最后的卷积层,输出通道的数量进一步增加。
# 在前两个卷积层之后,汇聚层不用于减少输入的高度和宽度
nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Flatten(),
# 这里,全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
nn.Linear(6400, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
# 最后是输出层。由于这里使用Fashion-MNIST,所以用类别数为10,而非论文中的1000
nn.Linear(4096, 10))
更多细节
因为卷积对位置比较敏感,而且对光照什么的都比较敏感,怎么让你变得不敏感,就是在数据中加入各种变种,训练的时候就模拟这种变化出来,这样神经网络记住数据的能力就变低了
复杂度对比
3.总结
- AlexNet 是更大更深的LeNet,10x参数个数,260x计算复杂度
- 新加入了dropout,relu,maxpooling,数据增强
- 标志着新一轮神经网络热潮开始了
使用块的网络 VGG
Alexnet最大的问题在于长得不规则,结构不甚清晰,也不便于调整。想要把网络做的更深更大需要更好的设计思想和标准框架。
1. VGG块
怎么样更好的更深更大?
直到现在更深更大的模型也是我们努力的方向,在当时AlexNet比LeNet更深更大得到了更好的精度,大家也希望把网络做的更深更大。选择之一是使用更多的全连接层,但全连接层的成本很高;第二个选择是使用更多的卷积层,但缺乏好的指导思想来说明在哪加,加多少。最终VGG采取了将卷积层组合成块,再把卷积块组合到一起的思路。
VGG块可以看作是AlexNet思路的拓展,AlexNet中将三个相同的卷积层放在一起再加上一个池化层,而VGG将其拓展成可以使用任意个3x3,不改变输入大小的的卷积层,最后加上一个2x2的最大池化层。
补充: 为什么使用2个3x3的卷积核可以代替5x5的卷积核?
55的计算量比较大,在同样计算开销的情况下,我堆叠33的效果比少量5*5的效果好
_第107张图片](http://img.e-com-net.com/image/info8/3471ff462a284f1eb1655abea3c2d572.jpg)
_第108张图片](http://img.e-com-net.com/image/info8/397debf5435a41e6847709ac29cc9eec.jpg)
为什么选择3x3卷积呢?在计算量相同的情况下选用更大的卷积核涉及对网络会越浅,VGG作者经过实验发现用3x3卷积的效果要比5x5好,也就是说神经网络库深且窄的效果会更好。
2. VGG架构
多个VGG块后接全连接层,不同次数的重复块得到不同的架构,如VGG-16, VGG-19等,后面的数字取决于网络层数。
可以讲VGG看作是将AlexNet中连续卷积的部分取出加以推广和复制,并删去了AlexNet中不那么规整的前几层。
![]()
- Alexnet是一个比较大的lenet,VGG是替换成n个VGG块串联在一起
- VGG较AlexNet相比性能有很大的提升,而代价是处理样本速度的降低和内存占用的增加。
3. 总结
![]()
这些思想影响了后面神经网络的设计,在之后的模型中被广泛使用。
4. 代码
定义VGG块
# 该函数有三个参数,分别对应于卷积层的数量 num_convs、输入通道的数量 in_channels 和输出通道的数量 out_channels.
import torch
from torch import nn
from d2l import torch as d2l
def vgg_block(num_convs, in_channels, out_channels):
layers = []
for _ in range(num_convs):
layers.append(
nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
layers.append(nn.ReLU())
in_channels = out_channels
layers.append(nn.MaxPool2d(kernel_size=2, stride=2))
return nn.Sequential(*layers)
实现VGG网络结构
'''
原始 VGG 网络有 5 个卷积块,其中前两个块各有一个卷积层,后三个块各包含两个卷积层。
第一个模块有 64 个输出通道,每个后续模块将输出通道数量翻倍,直到该数字达到 512。
由于该网络使用 8 个卷积层和 3 个全连接层,因此它通常被称为 VGG-11。'''
conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))
# vgg11
# 每个块的高度和块度减半,输出通道数量加倍,最终高度和宽度都是7,通道数为512。最后展平使用全连接层处理
def vgg(conv_arch):
conv_blks = []
in_channels = 1
# 卷积层部分
for (num_convs, out_channels) in conv_arch:
conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
in_channels = out_channels
return nn.Sequential(*conv_blks, nn.Flatten(),
# 全连接层部分
nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(),
nn.Dropout(0.5), nn.Linear(4096, 4096), nn.ReLU(),
nn.Dropout(0.5), nn.Linear(4096, 10))
net = vgg(conv_arch)
5. QA
Q1: 视觉领域人工特征的研究还有无进展?
现在在计算机视觉做人工特征是一种“政治不正确”的事,可能会因被认为没有novelty而发不出paper
老师认为人工特征提取确实应该被取代掉,随着技术进步可以把这部分工作交给机器,人去做更高级的事。
Q2: 需要学习特征值/特征向量/奇异值分解的知识吗?
这门课中不一定会讲,但很多深度学习模型用到矩阵分解的思想,但是用的不多,想学可以学。
网络中的网络(NiN)
![]()
LeNet、AlexNet 和 VGG 都有一个共同的设计模式:通过一系列的卷积层与池化层来提取空间结构特征;然后通过全连接层对特征的表征进行处理。AlexNet 和 VGG 对 LeNet 的改进主要在于如何扩大和加深这两个模块。
1. 动机
- 全连接层特别占用参数空间,重要的问题是他会带来过拟合
- 卷积层参数输入通道数输出通道数卷积核大小的平方
- 参数的大头就是卷积层之后的第一个全连接层,很容易过拟合,你需要做大量的正则化不要让这一层把你所有的东西都学了
- NiN的思想是完全不要全连接层
2. NiN块
核心思想:一个卷积层后面跟两个1x1的卷积层,后两层起到全连接层的作用。
![]()
1*1的卷积层等价于一个全连接层(可以理解成按照输入像素逐一做全连接层)(每个全连接层都有一个relu函数,增加非线性),在这里可以把每个通道数做一下变换
3. NiN架构
- 无全连接层
- 交替使用NiN块和步幅为2的最大池化层
逐步减小高宽和增大通道数 - 最后使用全局平均池化得到输出
其输入通道是类别数
4. NiN Networks
_第112张图片](http://img.e-com-net.com/image/info8/dfa21c95ab3548ea9ca03d1d3696e8ea.jpg)
NiN架构如上图右边所示,若干个NiN块(图示中为4个块)+池化层;前3个块后接最大池化层,最后一块连接一个全局平均池化层。
5. 总结
- NiN块结构:使用卷积层加两个1x1卷积层
后者对每个像素增加了非线性性 - NiN使用全局平均池化层来替代VGG和AlexNet中的全连接层
不容易过拟合,更少的参数个数
6.代码
NiN块
import torch
from torch import nn
from d2l import torch as d2l
# 定义NiN块
def nin_block(in_channels, out_channels, kernel_size, strides, padding):
return nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
nn.ReLU(), nn.Conv2d(out_channels, out_channels, kernel_size=1),
nn.ReLU(), nn.Conv2d(out_channels, out_channels, kernel_size=1),
nn.ReLU())
NiN模型
net = nn.Sequential(
nin_block(1, 96, kernel_size=11, strides=4, padding=0),
nn.MaxPool2d(3, stride=2),
nin_block(96, 256, kernel_size=5, strides=1, padding=2),
nn.MaxPool2d(3, stride=2),
nin_block(256, 384, kernel_size=3, strides=1, padding=1),
nn.MaxPool2d(3, stride=2), nn.Dropout(0.5),
# 标签类别数是10
nin_block(384, 10, kernel_size=3, strides=1, padding=1),
nn.AdaptiveAvgPool2d((1, 1)), #全局平均池化,高宽都变成1
nn.Flatten()) #消掉最后两个维度, 变成(batch_size, 10)
全局池化把输入变小了,而且他没有可学习的参数,主要好处是他把模型复杂度降低了,会提升泛化性。坏处就是收敛变慢了
GoogLeNet /inceptionv1
第一个可以超过1000层的卷积神经网络(卷积层的个数超过了1000)
含并行连结的网络(GoogLeNet)
GoogLeNet吸收了NiN中串联网络的思想,并在此基础上做了改进。我们往往不确定到底选取什么样的层效果更好,到底是3X3卷积层还是5X5的卷积层,诸如此类的问题是GooLeNet选择了另一种思路“小学生才做选择,我全都要”,这也使得GooLeNet成为了第一个模型中超过1000个层的模型。
_第113张图片](http://img.e-com-net.com/image/info8/ce7cddda32bc45f0b6dbe679f80f9486.jpg)
_第114张图片](http://img.e-com-net.com/image/info8/0194e7a132d54b519c971c541c652710.jpg)
Inception块
白色的1*1卷积可以理解为改变通道数的,蓝色的那个是用来抽取信息的(不抽取空间信息,只抽取通道信息)
![]()
为什么使用inception块?跟3 × 3 和 5 × 5的卷积层比起来,inception块有更少的参数个数和计算复杂度
_第116张图片](http://img.e-com-net.com/image/info8/3993e707683b447ab9e29d80a401332f.jpg)
GoogLeNet模型
GoogLeNet一共使用9个Inception块和全局平均汇聚层的堆叠来生成其估计值。Inception块之间的最大汇聚层可降低维度。 第一个模块类似于AlexNet和LeNet,Inception块的组合从VGG继承,全局平均汇聚层避免了在最后使用全连接层
_第117张图片](http://img.e-com-net.com/image/info8/734e437aadf944d4b308f22af8d2d5aa.jpg)
总结
-
Inception块相当于一个有4条路径的子网络。它通过不同窗口形状的卷积层和最大汇聚层来并行抽取信息,并使用1×1卷积层减少每像素级别上的通道维数从而降低模型复杂度。
-
GoogLeNet将多个设计精细的Inception块与其他层(卷积层、全连接层)串联起来。其中Inception块的通道数分配之比是在ImageNet数据集上通过大量的实验得来的。
-
GoogLeNet和它的后继者们一度是ImageNet上最有效的模型之一:它以较低的计算复杂度提供了类似的测试精度。
InceptionV2/V3
Inception v4
Inception v4 和 Inception -ResNet 在同一篇论文《Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning》中介绍
Inception v4 引入了专用的「缩减块」(reduction block),它被用于改变网格的宽度和高度。早期的版本并没有明确使用缩减块,但也实现了其功能。
_第127张图片](http://img.e-com-net.com/image/info8/0fffaf4e0ccc419bb2c83f13238d830b.jpg)
稠密连接网络(DenseNet)
ResNet中的跨层连接设计引申出了数个后续工作。本节我们介绍其中的一个:稠密连接网络(DenseNet) [1]。 它与ResNet的主要区别如图5.10所示。
_第128张图片](http://img.e-com-net.com/image/info8/f67b875b2209443da21bd4ca79e239f0.png)
图5.10 ResNet(左)与DenseNet(右)在跨层连接上的主要区别:使用相加和使用连结
图5.10中将部分前后相邻的运算抽象为模块A和模块B。与ResNet的主要区别在于,DenseNet里模块BB的输出不是像ResNet那样和模块AA的输出相加,而是在通道维上连结。这样模块A的输出可以直接传入模块B后面的层。在这个设计里,模块A直接跟模块B后面的所有层连接在了一起。这也是它被称为“稠密连接”的原因。
DenseNet的主要构建模块是稠密块(dense block)和过渡层(transition layer)。前者定义了输入和输出是如何连结的,后者则用来控制通道数,使之不过大。
5.12.1 稠密块
DenseNet使用了ResNet改良版的“批量归一化、激活和卷积”结构,我们首先在conv_block函数里实现这个结构。
import time
import torch
from torch import nn, optim
import torch.nn.functional as F
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
def conv_block(in_channels, out_channels):
blk = nn.Sequential(nn.BatchNorm2d(in_channels),
nn.ReLU(),
nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
return blk
稠密块由多个conv_block组成,每块使用相同的输出通道数。但在前向计算时,我们将每块的输入和输出在通道维上连结。
class DenseBlock(nn.Module):
def __init__(self, num_convs, in_channels, out_channels):
super(DenseBlock, self).__init__()
net = []
for i in range(num_convs):
in_c = in_channels + i * out_channels
net.append(conv_block(in_c, out_channels))
self.net = nn.ModuleList(net)
self.out_channels = in_channels + num_convs * out_channels # 计算输出通道数
def forward(self, X):
for blk in self.net:
Y = blk(X)
X = torch.cat((X, Y), dim=1) # 在通道维上将输入和输出连结
return X
在下面的例子中,我们定义一个有2个输出通道数为10的卷积块。使用通道数为3的输入时,我们会得到通道数为3+2×10=233+2×10=23的输出。卷积块的通道数控制了输出通道数相对于输入通道数的增长,因此也被称为增长率(growth rate)。
blk = DenseBlock(2, 3, 10)
X = torch.rand(4, 3, 8, 8)
Y = blk(X)
Y.shape # torch.Size([4, 23, 8, 8])
5.12.2 过渡层
由于每个稠密块都会带来通道数的增加,使用过多则会带来过于复杂的模型。过渡层用来控制模型复杂度。它通过1×1卷积层来减小通道数,并使用步幅为2的平均池化层减半高和宽,从而进一步降低模型复杂度。
def transition_block(in_channels, out_channels):
blk = nn.Sequential(
nn.BatchNorm2d(in_channels),
nn.ReLU(),
nn.Conv2d(in_channels, out_channels, kernel_size=1),
nn.AvgPool2d(kernel_size=2, stride=2))
return blk
对上一个例子中稠密块的输出使用通道数为10的过渡层。此时输出的通道数减为10,高和宽均减半。
blk = transition_block(23, 10)
blk(Y).shape # torch.Size([4, 10, 4, 4])
DenseNet模型
我们来构造DenseNet模型。DenseNet首先使用同ResNet一样的单卷积层和最大池化层。
net = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
类似于ResNet接下来使用的4个残差块,DenseNet使用的是4个稠密块。同ResNet一样,我们可以设置每个稠密块使用多少个卷积层。这里我们设成4,从而与上一节的ResNet-18保持一致。稠密块里的卷积层通道数(即增长率)设为32,所以每个稠密块将增加128个通道。
ResNet里通过步幅为2的残差块在每个模块之间减小高和宽。这里我们则使用过渡层来减半高和宽,并减半通道数。
num_channels, growth_rate = 64, 32 # num_channels为当前的通道数
num_convs_in_dense_blocks = [4, 4, 4, 4]
for i, num_convs in enumerate(num_convs_in_dense_blocks):
DB = DenseBlock(num_convs, num_channels, growth_rate)
net.add_module("DenseBlosk_%d" % i, DB)
# 上一个稠密块的输出通道数
num_channels = DB.out_channels
# 在稠密块之间加入通道数减半的过渡层
if i != len(num_convs_in_dense_blocks) - 1:
net.add_module("transition_block_%d" % i, transition_block(num_channels, num_channels // 2))
num_channels = num_channels // 2
同ResNet一样,最后接上全局池化层和全连接层来输出。
net.add_module("BN", nn.BatchNorm2d(num_channels))
net.add_module("relu", nn.ReLU())
net.add_module("global_avg_pool", d2l.GlobalAvgPool2d()) # GlobalAvgPool2d的输出: (Batch, num_channels, 1, 1)
net.add_module("fc", nn.Sequential(d2l.FlattenLayer(), nn.Linear(num_channels, 10)))
我们尝试打印每个子模块的输出维度确保网络无误:
X = torch.rand((1, 1, 96, 96))
for name, layer in net.named_children():
X = layer(X)
print(name, ' output shape:\t', X.shape)
输出:
0 output shape: torch.Size([1, 64, 48, 48])
1 output shape: torch.Size([1, 64, 48, 48])
2 output shape: torch.Size([1, 64, 48, 48])
3 output shape: torch.Size([1, 64, 24, 24])
DenseBlosk_0 output shape: torch.Size([1, 192, 24, 24])
transition_block_0 output shape: torch.Size([1, 96, 12, 12])
DenseBlosk_1 output shape: torch.Size([1, 224, 12, 12])
transition_block_1 output shape: torch.Size([1, 112, 6, 6])
DenseBlosk_2 output shape: torch.Size([1, 240, 6, 6])
transition_block_2 output shape: torch.Size([1, 120, 3, 3])
DenseBlosk_3 output shape: torch.Size([1, 248, 3, 3])
BN output shape: torch.Size([1, 248, 3, 3])
relu output shape: torch.Size([1, 248, 3, 3])
global_avg_pool output shape: torch.Size([1, 248, 1, 1])
fc output shape: torch.Size([1, 10])
小结
- 在跨层连接上,不同于ResNet中将输入与输出相加,DenseNet在通道维上连结输入与输出。
- DenseNet的主要构建模块是稠密块和过渡层。
BN批量归一化
深层神经网络的训练,尤其是使网络在较短时间内收敛是十分困难的,批量归一化[batch normalization] 是一种流行且有效的技术,能加速深层网络的收敛速度,目前仍被广泛使用。
训练深层网络时的问题
收敛速度慢:
- 由于训练时先正向传播后反向传播,且每层的梯度一般较小,若网络较深,则反向传播时会出现类似于梯度消失的现象,导致距离数据更近的层梯度较小,收敛慢,而距离输出更近的层梯度较大,收敛快。然而底部的层一般都用于提取较基础的特征信息(比如局部啊边缘啊很简单的纹理信息),上方的层收敛后,由于底部提取基础特征的层仍在变化,上方的层一直在不停的重新训练,导致整个网络难以收敛,训练较慢。
内部协变量转移:
- 分布偏移:偏移在视频课程中并未出现,但在《动手学深度学习》这本书中有提到过,在4.9. 环境和分布偏移部分。偏移指的是训练数据可能和测试数据的分布不同,比如利用来自真实的猫和狗的照片的训练数据训练模型,然后让模型去预测动画中的猫和狗的图片。
这显然会降低正确率也会对模型的进一步优化带来干扰。一般情况下对于分布偏移我们毫无办法,然而,在一些特定场景中,如果假定一些训练数据和测试数据分布的前提条件,就能对分布偏移进行处理,其中之一就是协变量偏移。
- 协变量偏移:协变量偏移假设输入的分布可能随时间变化,但标签函数(条件分布)没有改变。统计学家称这为协变量偏移(covariate shift)并给出了一些解决方案
- 内部协变量偏移(Internal Covariate Shift):每一层的参数在更新过程中,会改变下一层输入的分布,导致网络参数变幻莫测,难以收敛,神经网络层数越多,表现得越明显。
- 注意:
1:内部协变量偏移这个词与标准的协变量偏移所有区别。
2:能缓解内部协变量偏移仅仅是批量归一化的作者提出的假想,后续论文证实批量归一化实际对内部协变量偏移的缓解帮助不大
3:批量归一化一般只影响模型的收敛速度,不影响精度
过拟合:
- 由于网络深度加深,变得更为复杂,使得网络容易过拟合。
批量归一化
**批量归一化(batch normalization)**在 [Ioffe & Szegedy, 2015]中被提出,用于解决上述训练深度网络时的这些问题,然而这只是人们的感性理解,关于批量归一化具体是怎样帮助训练这个问题目前仍待进一步研究。
批量归一化尝试将每个训练中的mini-batch小批量数据(即会导致参数更新的数据)在每一层的结果进行归一化,使其更稳定,归一化指的是对于当前小批量中的所有样本,求出期望和方差,然后将每个样本减去期望再除以标准差。
形式化表达
- 批量归一化是一个线性变换,可以吧你的均值方差拉到比较好,让你的变化不那么剧烈
- 在卷积层中,我们将通道视作每个位置的特征,将每个样本中的每个位置视作一个样本进行计算。每个通道都有着自己的拉伸参数和偏移参数,所有通道加在一起组成了拉伸参数向量和偏移参数向量,若样本数为m,卷积输出为p*q,计算时对mpq个向量进行批量归一化运算(即视作有mpq个样本)
对(B,C,H,W)的输入,其针对哪些维度做归一化处理? B H W
![]()
![]()
_第134张图片](http://img.e-com-net.com/image/info8/151e3f064c0a439083c01b9a564c20be.jpg)
4. 因为均值和方差是在每一个随机的小批量上计算而来,是为噪音,另外两个参数是可学习的,可学习的东西变化不会太剧烈,取决于学习率。使得1.变化不要太剧烈2.有一定的随机性
5. 目前工程走在理论的前面,正不正确不知道
吴恩达老师深度学习课程中的批量归一化
吴恩达老师深度学习课程中的批量归一化中的部分内容与本课程有所出入,考虑到批量归一化这部分内容还没有精确的理论解释,目前的认识仅限于直觉,故将两课程中的区别即补充罗列在此作为参考:
- 关于dropout:
本课中提到批量归一化有正则化效果,无需再进行dropout
吴恩达老师课程中提到批量归一化正则化效果较差,不能作为正则化的手段,必要时需要dropout - 对于线性层(包括其他带有偏置项的层)后的批量归一化,由于归一化时减去了均值,偏置项被消掉,可以省略归一化层之前的偏置项
- 标准化的输入能使梯度下降加快,批归一化能使得每层的输入都被归一化,这也是训练更快的原因之一
- 批量归一化可以使得不同层之间互相的影响减少,从而应对数据偏移,增强鲁棒性。
从零实现BatchNorm
定义批量归一化
import torch
from torch import nn
from d2l import torch as d2l
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 通过 `is_grad_enabled` 来判断当前模式是训练模式还是预测模式
if not torch.is_grad_enabled():
# 如果是在预测模式下,直接使用传入的移动平均所得的均值和方差
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4)
if len(X.shape) == 2:
# 使用全连接层的情况,计算特征维上的均值和方差
mean = X.mean(dim=0)
var = ((X - mean)**2).mean(dim=0)
else:
# 使用二维卷积层的情况,计算通道维上(axis=1)的均值和方差。
# 这里我们需要保持X的形状以便后面可以做广播运算
mean = X.mean(dim=(0, 2, 3), keepdim=True)
var = ((X - mean)**2).mean(dim=(0, 2, 3), keepdim=True)
# 训练模式下,用当前的均值和方差做标准化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新移动平均的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta # 缩放和移位
return Y, moving_mean.data, moving_var.data
class BatchNorm(nn.Module):
# `num_features`:完全连接层的输出数量或卷积层的输出通道数。
# `num_dims`:2表示完全连接层,4表示卷积层
def __init__(self, num_features, num_dims):
super().__init__()
if num_dims == 2:
shape = (1, num_features)
else:
shape = (1, num_features, 1, 1)
# 参与求梯度和迭代的拉伸和偏移参数,分别初始化成1和0
self.gamma = nn.Parameter(torch.ones(shape))
self.beta = nn.Parameter(torch.zeros(shape))
# 非模型参数的变量初始化为0和1
self.moving_mean = torch.zeros(shape)
self.moving_var = torch.ones(shape)
def forward(self, X):
# 如果 `X` 不在内存上,将 `moving_mean` 和 `moving_var`
# 复制到 `X` 所在显存上
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device)
self.moving_var = self.moving_var.to(X.device)
# 保存更新过的 `moving_mean` 和 `moving_var`
Y, self.moving_mean, self.moving_var = batch_norm(
X, self.gamma, self.beta, self.moving_mean, self.moving_var,
eps=1e-5, momentum=0.9)
return Y
![]()
CPU和GPU
CPU
GPU
Alexnet比较大主要是因为他的全连接层
单机多卡并行
一台机器可以安装多个GPU(一般为1-16个),在训练和预测时可以将一个小批量计算切分到多个GPU上来达到加速目的,常用的切分方案有数据并行,模型并行,通道并行。
_第146张图片](http://img.e-com-net.com/image/info8/027cb23e628e418699f61d0d68d577dd.jpg)
数据并行
将小批量的数据分为n块,每个GPU拿到完整的参数,对这一块的数据进行前向传播与反向传播,计算梯度。
数据并行通常性能比模型并行更好,因为对数据进行划分使得各个GPU的计算内容更加均匀。
_第147张图片](http://img.e-com-net.com/image/info8/24f259725eb0460baa265e1ab3cca9ee.jpg)
数据并行的大致流程
![]()
主要分为五部
1:每个GPU读取一个数据块(灰色部分)
2:每个GPU读取当前模型的参数(橙色部分)
3:每个GPU计算自己拿到数据块的梯度(绿色部分)
4:GPU将计算得到的梯度传给内存(CPU)(绿色箭头)
5:利用梯度对模型参数进行更新(橙色箭头)
_第148张图片](http://img.e-com-net.com/image/info8/2644009e76ea47348734e2caac70ba07.jpg)
数据并行并行性较好,主要因为当每个GPU拿到的数据量相同时计算量也相似,各个GPU的运算时间相近,幸能较好
模型并行
将整个模型分为n个部分,每个GPU拿到这个部分的参数和负责上一个部分的GPU的输出作为输入来进行计算,反向传播同理。
模型并行通常用于模型十分巨大,参数众多,即使在每个mini-batch只有一个样本的情况下单个GPU的显存仍然不够的情况,但并行性较差,可能有时会有GPU处于等待状态。
通道并行
通道并行是数据并行和模型并行同时进行
总结
- 当一个模型能用单卡计算时,通常使用数据并行扩展到多卡
- 模型并行则用在超大模型上
Q&A(部分有价值的)
问1:若有4块GPU,两块显存大两块显存小怎么办?
答1: 若GPU运算性能相同,则训练取决于小显存的GPU的显存大小,更大的显存相当于浪费掉 若GPU运算性能不同,一般即为显存大的GPU性能更好,可以在分配数据时多分配一点
问2:数据拆分后,需存储的数据量会变大吗?会降低性能吗?
答2:每个GPU都单独存储了一份模型,这部分的数据量变大了,但如果只考虑运算时的中间变量,则中间变量的大小与数据量呈线性关系,每个GPU的数据小了,中间变量也会变小,所有GPU的中间变量加起来大小是不变的。 数据拆分后性能会变低,在下节课讲解(数据通讯的开销,每个GPU的batch-size变小可能无法跑满GPU,总batch-size变大则相同计算量下训练次数变少)
多GPU训练实现
_第149张图片](http://img.e-com-net.com/image/info8/ed279212721a4d268b7955ae8b76305b.jpg)
allreduce:每个GPU的梯度加起来,然后每个GPU再拿到自己的梯度
_第150张图片](http://img.e-com-net.com/image/info8/ae1690bcabc44324978f6192c07f0d76.jpg)
#数据累积和数据复制
def allreduce(data):
for i in range(1,len(data)):
data[0][:] += data[i].to(data[0].device)
for i in range(1,len(data)):
data[i][:] = data[0].to(data[i].device)
- 返回的损失ls是一个list,是每一个GPU上的损失
- 然后对每个GPU做反向传播,对每个GPU上的参数算一下梯度
- 做allreduce
- 每个GPU做自己的sgd
#小批量训练
def train_batch(X,y,device_params,devices,lr):
X_shards,y_shards = split_batch(X,y,devices)
#在每个GPU上分别计算损失
ls = [loss(lenet(X_shard,device_W),y_shard).sum() for X_shard,y_shard ,device_W in zip(X_shards,y_shards,device_params)]
for l in ls: #反向传播在每个GPU上分别执行
l.backward()
#将每个GPU的所有梯度相加,并将其广播到所有GPU
with torch.no_grad():
for i in range(len(device_params[0])):
allreduce([device_params[c][i].grad for c in range(len(devices))])
#在每个GPU上分别更新模型参数
for param in device_params:
d2l.sgd(param,lr,X.shape[0]) # 使用全尺寸的小批量
import torch
from torch import nn
from d2l import torch as d2l
#搭建ResNet18模型
def resnet18(num_classes,in_channels=1):
"""经过修改的ResNet18模型"""
def resnet_block(in_channels,out_channels,num_residuals,first_block=False):
blk = []
for i in range(num_residuals):
if i == 0 and not first_block:
blk.append(d2l.Residual(in_channels,out_channels,use_1x1conv=True,strides=2))
else:
blk.append(d2l.Residual(out_channels,out_channels))
return nn.Sequential(*blk)
#该模型使用了更小的卷积核、步长和填充,而且删除了最大汇聚层
net = nn.Sequential(
nn.Conv2d(in_channels,64,kernel_size=3,stride=1,padding=1),
nn.BatchNorm2d(64),
nn.ReLU())
net.add_module("resnet_block1",resnet_block(64,64,2,first_block=True))
net.add_module("resnet_block2",resnet_block(64,128,2))
net.add_module("resnet_block3",resnet_block(128,256,2))
net.add_module("resnet_block4",resnet_block(256,512,2))
net.add_module("global_avg_pool",nn.AdaptiveAvgPool2d((1,1)))
net.add_module("fc",nn.Sequential(nn.Flatten(),nn.Linear(512,num_classes)))
return net
net = resnet18(10)
#获得GPU列表
devices = d2l.try_all_gpus()
def train(net,num_gpus,batch_size,lr):
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size)
devices = [d2l.try_gpu(i) for i in range(num_gpus)]
#初始化网络
def init_weights(m):
if type(m) in [nn.Linear,nn.Conv2d]:
nn.init.normal_(m.weight,std=0.01)
net.apply(init_weights)
#在多个GPU上设置模型
net = nn.DataParallel(net,device_ids=devices)
trainer = torch.optim.SGD(net.parameters(),lr)
loss = nn.CrossEntropyLoss()
timer,num_epochs = d2l.Timer(),10
animator = d2l.Animator('epoch','test acc',xlim=[1,num_epochs])
for epoch in range(num_epochs):
net.train()
timer.start()
for X,y in train_iter:
trainer.zero_grad()
X,y = X.to(devices[0]),y.to(devices[0])
l = loss(net(X),y)
l.backward()
trainer.step()
timer.stop()
animator.add(epoch+1,(d2l.evaluate_accuracy_gpu(net,test_iter),))
print(f'test acc:{animator.Y[0][-1]:.2f},{timer.avg():.1f}s/round,'
f'at{str(devices)}')
Q2: 是否可以通过把resnet中的卷积层全替换成mlp来实现一个很深的网络?
可以,有这样做的paper,但是通过一维卷积(等价于全连接层)做的,如果直接换成全连接层很可能会过拟合。
//1*1卷积层等价于全连接层的特殊版本
Q3: 为什么batch norm是一种正则但只加快训练不提升精度?
老师也不太清楚并认为这是很好的问题,可以去查阅论文。
Q4: all_reduce, all_gather主要起什么作用?实际使用时发现pytorch的类似分布式op不能传导梯度,会破坏计算图不能自动求导,如何解决?
all_reduce是把n个东西加在一起再把所有东西复制回去,all_gather则只是把来自不同地方东西合并但不相加。使用分布式的东西会破坏自动求导,跨GPU的自动求导并不好做,老师不确定pytorch能不能做到这一功能,如果不能就只能手写。
Q5: 两个GPU训练时最后的梯度是把两个GPU上的梯度相加吗?
是的。mini-batch的梯度就是每个样本的梯度求和,多GPU时同理,每个GPU向将自己算的那部分样本梯度求和,最后再将两个GPU的计算得的梯度求和。
Q6: 为什么参数大的模型不一定慢?flop数多的模型性能更好是什么原理?
性能取决于每算一个乘法需要访问多少个bit,计算量与内存访问的比值越高越好。通常CPU/GPU不会被卡在频率上而是访问数据/内存上,所以参数量小,算力高的模型性能较好(如卷积,矩阵乘法)。
Q7: 为什么分布到多GPU上测试精度会比单GPU抖动大?
抖动是因为学习率变大了,**使用GPU数对测试精度没有影响,只会影响性能。**但为了得到更好的速度需要把batchsize调大,使得收敛情况发生变化,把学习率上调就使得精度更抖。
Q8: batchsize太大会导致loss nan吗?
不会,batchsize中的loss是求均值的,理论上batchsize更大数值稳定性会更好,出现数值不稳定问题可能是学习率没有调好。
Q9: GPU显存如何优化?
显存手动优化很难,靠的是框架,pytorch的优化做的还不错。除非特别懂框架相关技术不然建议把batchsize调小或是把模型做简单一点。
Q11: parameter server可以和pytorch结合吗,具体如何实现?
pytorch没有实现parameter server,但mxnet和tensorflow有。但是有第三方实现如byteps支持pytorch。
Q12: 用了nn.DataParallel(),是不是数据集也被自动分配到了多个GPU上?
是的。在算net.forward()的时候会分开。
Q13: 验证集准确率震荡大那个参数影响最大?
学习率。
Q14: 为了让网络前几层能够训练能否采用不同stage采用不同学习率的方法?
可以,主要的问题是麻烦,不好确定各部分学习率相差多少。
Q15: 在用torch的数据并行中将inputs和labels放到GPU0是否会导致性能问题,因为这些数据最终回被挪一次到其他GPU上。
数据相比梯度来说很少,不会对性能有太大影响。但这个操作看上去的确很多余,老师认为不需要做,但不这样做会报错。
Q16: 为什么batchsize较小精度会不怎么变化?
学习率太大了,batchsize小学习率就不能太大。
Q17: 使用两块不同型号GPU影响深度学习性能吗?
需要算好两块GPU的性能差。如一块GPU的性能是另一块的2倍,那么在分配任务时也应该分得2倍的任务量。保证各GPU在同样时间内算完同一部分。
分布式训练
分布式计算
本质上来说和之前讲的单机多卡并行没有区别。二者之间的区别是分布式计算是通过网络把数据从一台机器搬到另一台机器
_第157张图片](http://img.e-com-net.com/image/info8/2d94d775033f4e34b7571cea8d86cf5a.jpg)
GPU机器架构
总的来说,gpu到gpu的通讯是很快的,gpu到cpu慢一点。机器到机器更慢。因而总体性能的关键就是尽量在本地做通讯而少在机器之间做通讯
_第158张图片](http://img.e-com-net.com/image/info8/34432e0525294acbbc0a9155a742a694.jpg)
2.1 样例:计算一个小批量
- 每个worker从参数服务器那里获取模型参数:首先把样本复制到机器的内存,然后把样本分到每个gpu上
- 复制参数到每个gpu上:同样,先把每一次的参数放到内存里,然后再复制到每个gpu上
- 每个gpu计算梯度
- 再主内存上把所有gpu上的梯度加起来
- 梯度从主内存传回服务器
- 每个服务器对梯度求和,并更新参数
2.2 总结
由于gpu到gpu和gpu到内存的通讯速度还不错,因此我们尽量再本地做聚合(如梯度相加),并减少再网络上的多次通讯
关于性能
3.1 对于同步SGD:
- 这里每个worker都是同步计算一个批量,称为同步SGD
- 假设有n个gpu,每个gpu每次处理b个样本,那么同步SGD等价于再单gpu运行批量大小为nb的SGD
- 再理想情况下,n个gpu可以得到相对单gpu的n倍加速
3.2 性能:
_第161张图片](http://img.e-com-net.com/image/info8/818c3bed51af465dbf79ab9ec78e9588.jpg)
3…3 性能的权衡
_第162张图片](http://img.e-com-net.com/image/info8/69aaddc8bce1404f9158c8651e52efcc.jpg)
![]()
inception比33或者55的卷积要小,适合做并行
总结
- 分布式同步数据并行是多gpu数据并行在多机器上的拓展
- 网络通讯通常是瓶颈
- 需要注意使用特别大的批量大小时的收敛效率
- 更复杂的分布式有异步、模型并行(这里没有介绍)
数据增广
_第163张图片](http://img.e-com-net.com/image/info8/149a65c4936743d8afd00d8c7820180b.jpg)
_第164张图片](http://img.e-com-net.com/image/info8/30a79da867e74073ada4403763ea26da.jpg)
可以理解为一个正则项,作用在训练的时候。
_第165张图片](http://img.e-com-net.com/image/info8/6f7729f5329f4c51936d1bcf53bf2c0c.jpg)
_第166张图片](http://img.e-com-net.com/image/info8/1d78b928116649bbb9380780793744e9.jpg)
![]()
可以理解为增广没有改变均值但是改变了方差使得方差更大了
微调
_第167张图片](http://img.e-com-net.com/image/info8/fd947667bc384f88851f42b8bd1ec74f.jpg)
_第168张图片](http://img.e-com-net.com/image/info8/efd72efc7bfb4bb89c670f2c9e9bec78.jpg)
_第169张图片](http://img.e-com-net.com/image/info8/8b1e39c689e34b3888548d69315857c4.jpg)
_第170张图片](http://img.e-com-net.com/image/info8/cad2690d682d443e9b3eccad40e6dee1.jpg)
_第171张图片](http://img.e-com-net.com/image/info8/6436a479326d48f18cb2f622a28fe28a.jpg)
固定底层参数,你的模型复杂度变低了,模型变小了,所以可以认为是一个更强的正则化的效果 。在数据很小的情况下,全部训练参数很容易过拟合
![]()
![]()
数据不平衡主要是对上层影响比较大
![]()
微调对学习率不敏感,固定的就好
样式迁移
序列模型
序列数据及其统计工具
- 时序模型中,当前数据与之前的观察数据是相关的
- 自回归模型使用自身过去数据来预测未来
- 马尔科夫模型假设当前数据只根最近少数数据相关
- 潜变量模型使用潜变量来概括历史信息
对x1-x_t-1的数据进行建模,f()可以认为是一个机器学习模型
和之前不一样,之前是给定图片去预测他的标号,标号和图片不是一个东西,现在我的标号和数据样本其实是一个东西,所以叫做自回归模型(假设是回归的话)
马尔科夫假设
潜变量模型
RNN使用了隐藏层来记录过去发生的所有事件的信息,从而引入时序的特性,并且避免常规序列模型每次都要重新计算前面所有已发生的事件而带来的巨大计算量。
马尔科夫假设MLP模型训练
数据生成:
_第182张图片](http://img.e-com-net.com/image/info8/e2c1a276372245cba46781709b026a67.jpg)
马尔科夫假设:
![]()
_第183张图片](http://img.e-com-net.com/image/info8/125423211f2a407aa9308e0ae20d0640.jpg)
![]()
让我们看看这在实践中意味着什么。首先是检查模型对发生在下一个时间步的事情的预测能力有多好,也就是 单步预测(one-step-ahead prediction)。
_第184张图片](http://img.e-com-net.com/image/info8/5a969595e3c947ffa8d8c61042531efd.jpg)
在几个预测步骤之后,预测结果很快就会衰减到一个常数。为什么这个算法效果这么差呢?最终事实是由于错误的累积。
_第185张图片](http://img.e-com-net.com/image/info8/553be2302c4e48788d648a31bbc9e45b.jpg)
QA

两者不同,但是潜变量是可以用隐马尔科夫假设的(RNN就用了),潜变量是说我建模的时候是怎么建模,隐马尔可夫是说是和之前的多少数据相关
RNN循环神经网络
怎么吧潜变量自回归模型转化成RNN?
ot是用ht预测的输出,ht不能用xt(当前)而是用的h_t-1,计算损失的时候是ot和xt之间的关系计算损失
xt是用来更新
_第187张图片](http://img.e-com-net.com/image/info8/d5071f4d3daf4ccbbdbc536495a6090d.jpg)
最简单的RNN是通过W_hh存储时序信息的
流程如下,首先有一个输入序列,对于时刻t,我们用t-1时刻的输入xt-1和潜变量ht-1来计算新的潜变量ht。同时,对于t时刻的输出ot,则直接使用ht来计算得到。注意,计算第一个潜变量只需要输入即可(因为前面并不存在以往的潜变量)。
_第188张图片](http://img.e-com-net.com/image/info8/7cc4c8960c4242d684d963b433ec36de.jpg)
值得注意的是,RNN本质也是一种MLP,尤其是将ht-1这一项去掉时就完全退化成了MLP。RNN的核心其实也就是ht-1这一项,它使得模型可以和前面的信息联系起来,将时序信息储存起来,可以把RNN理解为是包含时序信息的MLP。
梯度裁剪
在T个时间步中进行反向传播,会由于产生O(T)长度的梯度乘法链,导致导数数值不稳定,这里使用一个限制θ,通常为5到10,来控制梯度乘法链的长度。使用如下的公式
![]()
就算就一个单隐藏层,但是我会做T= 35 步迭代,所以有点像一个长度为35层的MLP,至少是35层因为每步不止一个矩阵乘法,会发生梯度爆炸。
_第189张图片](http://img.e-com-net.com/image/info8/09d04c784d5c45c8aa9b9221a7be2f4e.jpg)
_第190张图片](http://img.e-com-net.com/image/info8/151f03e4a9f54a07ba842bfe04744e36.jpg)
等价于吧所有层的梯度拼在一起,再对他求L2 norm
_第191张图片](http://img.e-com-net.com/image/info8/5d96cd31d58e454a9478c50c3deed536.jpg)
_第192张图片](http://img.e-com-net.com/image/info8/269a75cd846743b1862aaa81007384bf.jpg)
梯度爆炸解决策
大于某一个threshold,方向保持,步长按threshold。
![]()
梯度弥散
后面层梯度能得到有效更新,数值计算的原因,到前面层梯度已经很小了,参数不能得到很好更新,这就是梯度弥散,梯度弥散在下一节LSTM中介绍。
更多的RNNs
门控循环单元GRU
1. 动机:如何关注一个序列
-
做RNN的时候处理不了太长的序列,这是因为你把序列学习全部放在一个隐藏状态里面,所有东西都放进去,当时间很长的时候隐藏状态可能就累计了太多东西了,对于刚开始的学习以及不太容易抽取出来了。
-
并不是所有的观察值都同等重要,比如电影的帧与帧其实都差不多,就是场景切换的时候可能会很重要。但是RNN没有这种机制
_第194张图片](http://img.e-com-net.com/image/info8/2ef721ab424d4ff8b41b71c7497a67b0.jpg)
想只记住相关的观察需要:
3. 能关注的机制(更新门):顾名思义,是否需要根据我的输入,更新隐藏状态
4. 能遗忘的机制(重置门):更新候选项时,是否要考虑前一隐藏状态。
GRU网络对LSTM网络的改进有两个方面:
1、将遗忘门和输入门合并为一个门:更新门,此外另一门叫做重置门。
2、不引入额外的内部状态c,直接在当前状态ht和历史状态ht-1之间引入线性依赖关系。
2. 门的概念
下图描述了门控循环单元中的重置门和更新门的输入,输入是由当前时间步的输入和前一时间步的隐藏状态给出。两个门的输出是由使用 sigmoid 激活函数的两个全连接层给出。
-
更新门Zt,重置门Rt的公式大体相同,唯一不同的是学习到的参数。
-
需要注意的是,计算门的方式和原来RNN的实现中计算新的隐状态相似,只是激活函数改成了sigmoid。
-
门本来是电路中的一个概念,0,1代表不同的电平,可以用于控制电路的通断。此处sigmoid将门的数值归一化到0到1之间,是一种"软更新"方式。而从后面的公式上可以看出,本讲课程采用的是低电平有效(越靠近0,门的作用越明显)的方式控制。
3. 候选隐状态
在RNN中,这个所谓的候选隐状态就是当前步的隐状态(Rt无限接近1时)。但是由于引入了更新门,我们需要考虑是直接沿用上一步的隐藏状态,还是像RNN一样使用当前步计算的隐状态。所以这个结合了当前输入计算的隐状态,不能立马变成当前的Ht,而是需要用更新门和前一隐状态做一个加权,所以它是一个候选项。
4. 真正的隐状态
![]()
~H_t会看Ht-1和Xt,Z尽量不看Xt
用更新门对候选隐状态和前一隐状态做加权,得到当前步隐状态的值。
如果zt无限接近于0,更新起作用,候选隐状态“转正”,变为当前隐状态。
如果zt无限接近于1,更新不起作用,当前隐状态还是沿用前一隐状态。
5. 总结
_第199张图片](http://img.e-com-net.com/image/info8/4b0fee4baee044cb8341bf124db64c3b.jpg)
上图四行公式概括了GRU模型。在RNN的基础上,最重要的是引入了更新门和重置门,来决定前一隐状态对当前隐状态的影响。以最开始的猫鼠序列的例子来说,如果我的模型一直看到猫,模型可以学习到隐状态不怎么去更新,于是隐状态一直保留了猫的信息,而看到老鼠,隐状态才进行更新。
_第200张图片](http://img.e-com-net.com/image/info8/5c8337b52068408d8ae74c67a12876cc.jpg)
- 这些设计可以帮助我们处理循环神经网络中的梯度消失问题,并更好地捕获时间步距离很长的序列的依赖关系。
- 例如,如果整个子序列的所有时间步的更新门都接近于 1,则无论序列的长度如何,在序列起始时间步的旧隐藏状态都将很容易保留并传递到序列结束。
一个与RNN的联动在于:
如果更新门完全发挥作用(无限接近于0),重置门不起作用(无限接近于1),此时GRU模型退化为RNN模型。
6. QA
问题:GRU为什么需要两个门?
-
重置门和更新门各司其职。重置门单方面控制自某个节点开始,之前的记忆(隐状态)不在乎了,直接清空影响,同时也需要更新门帮助它实现记忆的更新。更新门更多是用于处理梯度消失问题,可以选择一定程度地保留记忆,防止梯度消失。
-
重置门影响的是当前步新的候选隐状态的计算,更新门影响的是当前步隐状态的更新程度。
长短期记忆网络(LSTM)
什么是长短期记忆?
在循环神经网络中,记忆能力分为短期记忆、长期记忆和长短期记忆。
1、短期记忆
短期记忆指简单循环神经网络中的隐状态h。因为隐状态h存储了历史信息,但是隐状态每个时刻都会被重写,因此可以看做是一种短期记忆(short-term memory)。
2、长期记忆
长期记忆指神经网络学习到的网络参数。因为网络参数一般是在所有“前向”和“后向”计算都完成后,才进行更新,隐含了从所有训练数据中学习到的经验,并且更新周期要远远慢于短期记忆,所以看做是长期记忆(long-term memory)。
3、长短期记忆
在LSTM网络中,由于遗忘门的存在,如果选择遗忘大部分历史信息,则内部状态c保存的信息偏于短期,而如果选择只遗忘少部分历史信息,那么内部状态偏于保存更久远的信息,所以内部状态c中保存信息的历史周期要长于短期记忆h,又短于长期记忆(网络参数),因此称为长短期记忆(long short-term memory)。
1.长短期记忆网络:
_第201张图片](http://img.e-com-net.com/image/info8/8b6ac76f0fa2434380651e6336433cf3.jpg)
可以说,长短期记忆网络的设计灵感来自于计算机的逻辑门。 长短期记忆网络引入了记忆元(memory cell),或简称为单元(cell)。 有些文献认为记忆元是隐状态的一种特殊类型, 它们与隐状态具有相同的形状,其设计目的是用于记录附加的信息。 为了控制记忆元,我们需要许多门。 其中一个门用来从单元中输出条目,我们将其称为输出门(output gate)。 另外一个门用来决定何时将数据读入单元,我们将其称为输入门(input gate)。 我们还需要一种机制来重置单元的内容,由遗忘门(forget gate)来管理, 这种设计的动机与门控循环单元相同, 能够通过专用机制决定什么时候记忆或忽略隐状态中的输入。 让我们看看这在实践中是如何运作的。
1.1 门
1.2 候选记忆单元
Ct_hat 跟之前RNN的更新计算是一样的
_第203张图片](http://img.e-com-net.com/image/info8/025f2d76f98a4a1eb72bced6d8aaf6e6.jpg)
相当于在ht-1到ht的预测中又加了一层隐藏单元
_第204张图片](http://img.e-com-net.com/image/info8/7deafc002a754583b06d5c4e5bc19320.jpg)
1.3 记忆单元
_第205张图片](http://img.e-com-net.com/image/info8/6f3d83f83fe54cf1a8cae34db3cd99f6.jpg)
如果遗忘门始终为(1)且输入门始终为(0), 则过去的记忆元 将随时间被保存并传递到当前时间步。 引入这种设计是为了缓解梯度消失问题, 并更好地捕获序列中的长距离依赖关系。
![]()
_第206张图片](http://img.e-com-net.com/image/info8/93c7762a97b24ee797535442289b1fe1.jpg)
LSTM 的关键就是记忆单元,水平线在图上方贯穿运行。
记忆单元类似于传送带。直接在整个链上运行,只有一些少量的线性交互。信息在上面流传保持不变会很容易。
![]()
H是一个[-1,1]之间的数字,C可以用来存储信息,他可以做到比较大,是没有数值限制的
1.4 隐状态
记忆单元经过计算达到[-2,+2],所以我还想隐状态在[-1,1]之间的话需要再做一次tanh
_第207张图片](http://img.e-com-net.com/image/info8/407cbd40647c4c2ea44aa01ba2bc993b.jpg)
最后,我们需要定义如何计算隐状态, 这就是输出门发挥作用的地方。 在长短期记忆网络中,它仅仅是记忆元的的门控版本。 这就确保了Ht的值始终在区间((-1, 1))内.
只要输出门接近1,我们就能够有效地将所有记忆信息传递给预测部分, 而对于输出门接近(0),我们只保留记忆元内的所有信息,而不需要更新隐状态。
![]()
深度循环神经网络
双向循环神经网络
- 第一个隐藏层正常输,第二个隐藏层吧输入反一下,再把输出反一下,然后输出去和前一个的输出一一对应的做concat
- 正向和反向的weight是concate在一起的,不是相加或者其他操作
双向循环神经网络的错误应用
编码器解码器结构
Seq2Seq
- 编码器吧最后一个隐藏状态传给解码器,这个隐藏状态包括这个句子的信息
- 双向可以做encoder不能做decoder
- decoder吧上一个时间步的输出当做输入,同时隐藏状态也过来
_第216张图片](http://img.e-com-net.com/image/info8/a62b98c5cdc04b05ad93cb3dea27db59.jpg)
_第217张图片](http://img.e-com-net.com/image/info8/824300f1339140d98400952c00244d9e.jpg)
- 训练的时候是用真正的target输入,就算上一时刻输出错了也没关系
- 推理和训练不一样
_第218张图片](http://img.e-com-net.com/image/info8/b2a7729e4d0f48eaba11320758686cc0.jpg)
_第219张图片](http://img.e-com-net.com/image/info8/47eedbba19d14353aed5b6163e6e9d1a.jpg)
_第220张图片](http://img.e-com-net.com/image/info8/89d991244a6647c198c2789a256a8fd3.jpg)
注意力机制
- 最大池化就是把最大的抽出来,我也不知道要干嘛,反正就把最大的东西抽出来;卷积的话就是一个核,就把所有的东西都弄出来,一般是比较容易抽取的特征被抽取出来,比如大量的像素和饱和的颜色
- 随意线索就是你想要干嘛,key和value就是环境那些不随意线索,比如报纸咖啡杯等等都是一些环境中的东西,他的本身叫做key,他会对应一个value,key和value可以是一样可以是不一样,咖啡杯那个东西就是key,就是他的属性,value就是他对我有什么用
- 注意力机制也可以叫做quary pooling,他会根据你的quary去做一些有偏向性的选择一些键值对,quary相当于有自己的想法我要干嘛,区别于之前层在于显式的加入了quary这个东西——根据我的查询去寻找我感兴趣的东西
_第222张图片](http://img.e-com-net.com/image/info8/ed947788866045c0b623159cbba319e9.jpg)
![]()
_第223张图片](http://img.e-com-net.com/image/info8/fb7a469ffab14e1eb277209d6dfce9e2.jpg)
_第224张图片](http://img.e-com-net.com/image/info8/242379bc3e7943fa99959383fd5cfca9.jpg)
_第225张图片](http://img.e-com-net.com/image/info8/0514de98a8e24872864b97cb653a407c.jpg)
之前的那些东西都是用不随意线索,不能是你告诉我你想要什么东西,只能说给我一个数据我自己去看
注意力分数
掩蔽softmax操作
正如上面提到的,softmax操作用于输出一个概率分布作为注意力权重。 在某些情况下,并非所有的值都应该被纳入到注意力汇聚中。 例如,为了在 9.5节中高效处理小批量数据集, 某些文本序列被填充了没有意义的特殊词元。 为了仅将有意义的词元作为值来获取注意力汇聚, 我们可以指定一个有效序列长度(即词元的个数), 以便在计算softmax时过滤掉超出指定范围的位置。 通过这种方式,我们可以在下面的masked_softmax函数中 实现这样的掩蔽softmax操作(masked softmax operation), 其中任何超出有效长度的位置都被掩蔽并置为0。
import math
import torch
from torch import nn
from d2l import torch as d2l
# 掩码Softmax操作
def masked_softmax(X, valid_lens):
"""通过在最后一个轴上遮盖元素来执行 softmax 操作"""
# `X`: 3D tensor, `valid_lens`: 1D or 2D tensor
if valid_lens is None:
return nn.functional.softmax(X, dim=-1)散
else:
shape = X.shape
if valid_lens.dim() == 1:
valid_lens = torch.repeat_interleave(valid_lens, shape[1])
else:
valid_lens = valid_lens.reshape(-1)
# 在最后的轴上,被遮盖的元素使用一个非常大的负值替换,从而其 softmax (指数)输出为 0
X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens,
value=-1e6)
return nn.functional.softmax(X.reshape(shape), dim=-1)
# 考虑由两个 2 × 4 矩阵表示的样本组成的小批量数据集,其中这两个样本的有效长度分别为 2 和 3。
# 经过掩码 softmax 操作,超出有效长度的值都被遮盖为零。
masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3]))
tensor([[[0.3966, 0.6034, 0.0000, 0.0000],
[0.4718, 0.5282, 0.0000, 0.0000]],
[[0.4841, 0.2792, 0.2368, 0.0000],
[0.4889, 0.2826, 0.2285, 0.0000]]])
# 同样,我们也可以使用二维张量为每个矩阵示例中的每一行指定有效长度。
masked_softmax(torch.rand(2, 2, 4), torch.tensor([[1, 3], [2, 4]]))
tensor([[[1.0000, 0.0000, 0.0000, 0.0000],
[0.4509, 0.2201, 0.3290, 0.0000]],
[[0.5237, 0.4763, 0.0000, 0.0000],
[0.1962, 0.4115, 0.2280, 0.1643]]])
可加性注意力
在设计可加性注意力层之前,我们先准备一些需要用到的函数
然后开始生成可加性注意力层:
class AdditiveAttention(nn.Module):
"""可加性注意力"""
def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
super(AdditiveAttention, self).__init__(**kwargs)
self.W_k = nn.Linear(key_size, num_hiddens, bias=False)
self.W_q = nn.Linear(query_size, num_hiddens, bias=False)
self.w_v = nn.Linear(num_hiddens, 1, bias=False)
self.dropout = nn.Dropout(dropout)
def forward(self, queries, keys, values, valid_lens):
queries, keys = self.W_q(queries), self.W_k(keys)
# 在维度扩展后,
# `queries` 的形状:(`batch_size`, 查询的个数, 1, `num_hidden`)
# `key` 的形状:(`batch_size`, 1, “键-值”对的个数, `num_hiddens`)
# 使用广播方式进行求和=>feature的形状(batch_size,query个数,key-alue对个数,num_hiddens)
features = queries.unsqueeze(2) + keys.unsqueeze(1) # 将特征增加一个维度
features = torch.tanh(features)
# `self.w_v` 仅有一个输出,因此从形状中移除最后那个维度。
# `scores` 的形状:(`batch_size`, 查询的个数, “键-值”对的个数)
scores = self.w_v(features).squeeze(-1)
self.attention_weights = masked_softmax(scores, valid_lens)
# `values` 的形状:(`batch_size`, “键-值”对的个数, 值的维度)
return torch.bmm(self.dropout(self.attention_weights), values)
queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
# `values` 的小批量数据集中,两个值矩阵是相同的
values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(2, 1, 1)
valid_lens = torch.tensor([2, 6])
attention = AdditiveAttention(key_size=2, query_size=20, num_hiddens=8,
dropout=0.1)
attention.eval()
print("queries:",queries.shape)
print("keys:",keys.shape)
print("values:",values.shape)
attention(queries, keys, values, valid_lens)
queries: torch.Size([2, 1, 20])
keys: torch.Size([2, 10, 2])
values: torch.Size([2, 10, 4])
tensor([[[ 2.0000, 3.0000, 4.0000, 5.0000]],
[[10.0000, 11.0000, 12.0000, 13.0000]]], grad_fn=<BmmBackward0>)
缩放的“点-积”注意力
使用“点-积”可以得到计算效率更高的评分函数。但是**“点-积”操作要求查询和键具有相同的矢量长度 d 。**
使用注意力机制的seq2seq
-
s2s只传了最后的隐藏状态过去,当然你也可以说最后的隐藏的状态以及有了之前的信息,但是你需要从这里还原出来位置的信息,所以动机是翻译对应的词的时候,我的注意力关注在原句子对应的部分
-
输出作为quary是因为假设RNN的输出都是在一个语义空间里面,所以用输出不用embedding的输入,因为key value也是RNN的输出,key和quary匹配的时候最好也用RNN的输出,这样差不多在一个同样的语义空间里面
自注意力和位置编码
自注意力
![]()
你可以认为,我给定一个序列,其实有点像RNN,qkv是一个东西的情况下可以用自注意力这种东西来处理序列,不需要之前一定要有encoder-decoder,qkv都是来自于自己
_第236张图片](http://img.e-com-net.com/image/info8/1b5196e256d842b1ae767bacb6ca47a0.jpg)
位置编码
class PositionalEncoding(nn.Module):
def __init__(self, num_hiddens, dropout, max_len=1000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(dropout)
# Create a long enough `P`
self.P = torch.zeros((1, max_len, num_hiddens))
X = torch.arange(max_len, dtype=torch.float32).reshape(
-1, 1) / torch.pow(
10000,
torch.arange(0, num_hiddens, 2, dtype=torch.float32) /
num_hiddens)
self.P[:, :, 0::2] = torch.sin(X)
self.P[:, :, 1::2] = torch.cos(X)
def forward(self, X):
X = X + self.P[:, :X.shape[1], :].to(X.device)
return self.dropout(X)
encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])
_第239张图片](http://img.e-com-net.com/image/info8/e27fd6bbf4b94d6682871e142ed0c5e8.jpg)
使用sin cos的好处是他编码的是相对的位置信息,可以通过一个线性变换W来给你找出来,这样鼓励
_第240张图片](http://img.e-com-net.com/image/info8/33362eb3bf844f53b5f15991eaab2194.jpg)
_第241张图片](http://img.e-com-net.com/image/info8/a266f801b33042a8aaf8ef2c7df582d0.jpg)
Transformer
1.transformer架构
2.多头注意力
_第243张图片](http://img.e-com-net.com/image/info8/7cf5cd491cd648ffa19786435786db7f.jpg)
多头有点像卷积里面的多通道,但是这里已经有多通道了,所以叫multi-head
3.有掩码的多头注意力
4.基于位置的前馈网络
5.层归一化
BN需要序列长度一致,导致不稳定;训练和预测的长度本来就不一样,预测会变得越来越长
6.信息传递
7.预测
总结
QA
- 多头注意力,concat和相加取平均怎么选择?
老师认为concat保留的信息更全面,更好 - 为什么在获取词向量之后,需要对词向量进行缩放(乘以embedding size的开方之后再加上PE)
embedding之后,向量长度变长,元素值变小,乘以之后可以保证在-1,1之间,和position大小差不多 - num of head是什么?
类似卷积的多通道,多个attention关注的是不同的特征
BERT
优化算法
凸集:一个集合任意找两个点,两个点的连线都在这个集合里面
凸函数:函数上随便取两个点,保证整个函数在两点连线下面
_第256张图片](http://img.e-com-net.com/image/info8/dfb030e871484df3ba8afb9eb2869083.jpg)
_第257张图片](http://img.e-com-net.com/image/info8/307c8aae51e649e38e96f758bf36d081.jpg)
_第258张图片](http://img.e-com-net.com/image/info8/18c1958dacc241beb39d59e4426103a0.jpg)
- 包括一个隐藏层的MLP,因为他的激活函数是非线性的,非线性是非凸的
- 卷积本身是线性,但是加了激活函数就不是了
凸函数的表达能力是非常有限的,优化大多是凸的
_第262张图片](http://img.e-com-net.com/image/info8/aa9cdc324e18476bbef63e8596082610.jpg)
loss平面比较复杂比较陡的时候,平滑的改变方向(SGD,0.9)
Adam对学习率没有那么敏感,做了非常多的平滑(可以认为是一个非常非常平滑的SGD)
_第1张图片](http://img.e-com-net.com/image/info8/7a06013652d04b40b7c7b12946b32f7e.jpg)
_第2张图片](http://img.e-com-net.com/image/info8/b230d35703f34297959763e1ab8ee14b.jpg)
_第3张图片](http://img.e-com-net.com/image/info8/0726eb091f5b4d279614d67caaa2570a.jpg)
_第5张图片](http://img.e-com-net.com/image/info8/8e2988e316a645f5a8a580793856a2c6.jpg)
_第6张图片](http://img.e-com-net.com/image/info8/5b49a297a82a4a76aeed86d4eb2717bb.jpg)
_第7张图片](http://img.e-com-net.com/image/info8/8dbf94c25fb143629a7633f72eeb4aca.jpg)
_第8张图片](http://img.e-com-net.com/image/info8/4d7618c7c0c64567a65aaffc9d2283ab.jpg)
_第9张图片](http://img.e-com-net.com/image/info8/3e4c540754914fc7b94f91603042bd02.jpg)
_第10张图片](http://img.e-com-net.com/image/info8/03ec003394174f158102b9d08a4d47d0.jpg)
_第11张图片](http://img.e-com-net.com/image/info8/925594f73f7745d4bbf0e3d6f4ca94d5.jpg)
_第12张图片](http://img.e-com-net.com/image/info8/15d887fe55d7469aac8a61a00e4ee6cc.jpg)
_第13张图片](http://img.e-com-net.com/image/info8/61a9f365c3144172a43a87fd55e3f119.jpg)
_第14张图片](http://img.e-com-net.com/image/info8/a0b1fa070df54ceea68e0b6bd85645da.jpg)
_第15张图片](http://img.e-com-net.com/image/info8/f058d5ae090641febdd666533b4d6d3e.jpg)
_第17张图片](http://img.e-com-net.com/image/info8/96bffe87b75b45e58c470f3399bfac86.jpg)
_第18张图片](http://img.e-com-net.com/image/info8/2a3f5649060d46e588b4cf287d80fb43.jpg)
_第19张图片](http://img.e-com-net.com/image/info8/2595c7cdff384fdc8d58ba5c68249e08.jpg)
_第20张图片](http://img.e-com-net.com/image/info8/d050b28fac97417c97b023cc04c91bfb.jpg)
_第21张图片](http://img.e-com-net.com/image/info8/5a2a8b5144a54c18a5382daa3de08443.jpg)
_第22张图片](http://img.e-com-net.com/image/info8/0f1fd612c2574c96be89bd0872219ece.jpg)
_第23张图片](http://img.e-com-net.com/image/info8/c70a37d567364bf89bed415a0786fc62.jpg)
_第27张图片](http://img.e-com-net.com/image/info8/7d14f7cd66794c8d857d2f9ad6c0fe4e.jpg)
_第28张图片](http://img.e-com-net.com/image/info8/5a9ce84b80af48b69ecda20dfb3d9894.jpg)
_第29张图片](http://img.e-com-net.com/image/info8/9ccd2407f9cb4bc78ca5eb5b6364eb2b.jpg)
_第30张图片](http://img.e-com-net.com/image/info8/c45dd7e5e31a4766a86dde0671322187.jpg)
_第31张图片](http://img.e-com-net.com/image/info8/8ac009fa28734388b6c2c7ebc4b367ae.jpg)
_第36张图片](http://img.e-com-net.com/image/info8/384e73eb5ea54910b6fd034fd2fbc4ea.jpg)
_第37张图片](http://img.e-com-net.com/image/info8/0f9b509ef9674cbb80d7469a4125595d.jpg)
_第44张图片](http://img.e-com-net.com/image/info8/1bf88c960f8d4f5dbe18ad387f327f03.png)

_第53张图片](http://img.e-com-net.com/image/info8/92afa5f1795a41adbf10f82f1ff55f29.jpg)
_第55张图片](http://img.e-com-net.com/image/info8/9165e34754e048ee82bb1ecce5ef1c0f.jpg)
_第64张图片](http://img.e-com-net.com/image/info8/f6327c809f5b4daca4ed7caaa3c6c91b.jpg)
_第67张图片](http://img.e-com-net.com/image/info8/cdffd00bf1d540a78845ecd8bbc13deb.jpg)
_第68张图片](http://img.e-com-net.com/image/info8/2f905f4b645f4882918c7511191d1b76.jpg)
_第71张图片](http://img.e-com-net.com/image/info8/c0d966dbcdd2426685b8d1810c483b81.jpg)
_第72张图片](http://img.e-com-net.com/image/info8/220612c8ba764641aed613b000ccd78c.jpg)
_第80张图片](http://img.e-com-net.com/image/info8/03e48c2b4ebf4ce6af468b29b2788a75.jpg)
_第83张图片](http://img.e-com-net.com/image/info8/6cac5611482749dc98111228c85379c1.jpg)
_第84张图片](http://img.e-com-net.com/image/info8/6fa8df7196e54af8938acff3d03e72df.jpg)
_第85张图片](http://img.e-com-net.com/image/info8/9098b30038214c77952fce0ae607e0a2.jpg)
_第86张图片](http://img.e-com-net.com/image/info8/126aac946690418ea2281bc7da63efea.jpg)
_第87张图片](http://img.e-com-net.com/image/info8/0174edc1af6343d4860f7e425608a27f.jpg)
_第91张图片](http://img.e-com-net.com/image/info8/9bcebce22c974594adb31256b7b263c3.jpg)
_第92张图片](http://img.e-com-net.com/image/info8/e3f2101b0f134a56b43c4b48e6994fe4.jpg)
_第93张图片](http://img.e-com-net.com/image/info8/a01d30a7dd6d464a866ef5b709cb1bf7.jpg)
_第94张图片](http://img.e-com-net.com/image/info8/c6e6a7ff1639468888f7d009af61d860.jpg)
_第95张图片](http://img.e-com-net.com/image/info8/c5fdf8a1b9e542b482c30c5bb65680a9.jpg)
_第96张图片](http://img.e-com-net.com/image/info8/1ff3a702edb840cfad1ef4546c9c4ddd.jpg)
_第97张图片](http://img.e-com-net.com/image/info8/ca0e8f48ca13408cb274247e19bff7ab.jpg)
_第98张图片](http://img.e-com-net.com/image/info8/e16a2bff3c4e43088cf61951609514d5.jpg)
_第99张图片](http://img.e-com-net.com/image/info8/1a7d490e532b4710a0b40fb1ce745261.jpg)
_第100张图片](http://img.e-com-net.com/image/info8/cf99b755e1cf46f4bf4b9dc1205ecc26.jpg)
_第101张图片](http://img.e-com-net.com/image/info8/b601586fc4e5454d8e6cd6ba247b106e.jpg)
_第102张图片](http://img.e-com-net.com/image/info8/f63b6256ce1849c794fb0c754817a56a.jpg)
_第103张图片](http://img.e-com-net.com/image/info8/5a64fcd84f364b16862122a6868fa780.jpg)
_第104张图片](http://img.e-com-net.com/image/info8/40246845542a4297a8a6f1df2fd59158.jpg)
_第105张图片](http://img.e-com-net.com/image/info8/4002685402eb4fb29776ead3edb76aaf.jpg)
_第106张图片](http://img.e-com-net.com/image/info8/25613a1c32d040fa9ef32dd0777ae48b.jpg)
_第109张图片](http://img.e-com-net.com/image/info8/13bfea5b2bf944e7a7ea3eee5bf041fa.jpg)
_第110张图片](http://img.e-com-net.com/image/info8/20adc95b55204d8daee9e29f0b748bbf.jpg)
_第111张图片](http://img.e-com-net.com/image/info8/9aaa0bebe22d4a21b71a0e198175f29f.jpg)
_第115张图片](http://img.e-com-net.com/image/info8/8c9be526ad15497bbcdeec99d1812fc6.jpg)
_第118张图片](http://img.e-com-net.com/image/info8/11f0c9d394344561b00d756d37e91195.jpg)
_第119张图片](http://img.e-com-net.com/image/info8/8b77d1be6eae4e9baef4ecb2f43c63bd.jpg)
_第120张图片](http://img.e-com-net.com/image/info8/f6c8d92137d04d0493f3a937b9917258.jpg)
_第121张图片](http://img.e-com-net.com/image/info8/d48131cf05a34a11829a041b2a82af6a.jpg)
_第122张图片](http://img.e-com-net.com/image/info8/4d954a841a8e45718678eb643566c0e8.jpg)
_第123张图片](http://img.e-com-net.com/image/info8/7f97c23538a3475bb857b196460612d1.jpg)
_第124张图片](http://img.e-com-net.com/image/info8/365140a6a30643a8a2175de14c36be5c.jpg)
_第125张图片](http://img.e-com-net.com/image/info8/94e8946948b944b69330460c8a8a705d.jpg)
_第126张图片](http://img.e-com-net.com/image/info8/ffce3d7333a8427eb84466967a9e407e.jpg)
_第129张图片](http://img.e-com-net.com/image/info8/3fa3527e37af4d5c8a7bd05115303ddc.jpg)
_第130张图片](http://img.e-com-net.com/image/info8/b7f203f0b7fa46efadb761c039e124c1.jpg)
_第131张图片](http://img.e-com-net.com/image/info8/1d4206a1a1df4e3e8567559deb128167.jpg)
_第132张图片](http://img.e-com-net.com/image/info8/c46dc919730144388b6caf7354b0ae07.jpg)
_第133张图片](http://img.e-com-net.com/image/info8/70b87f5f7cd74671908a897f2683e67b.jpg)
_第135张图片](http://img.e-com-net.com/image/info8/04132727ef50438f994c56291da241e6.jpg)
_第136张图片](http://img.e-com-net.com/image/info8/937f716f2e324024918ed0a7ee20414c.jpg)
_第137张图片](http://img.e-com-net.com/image/info8/f3b69a7732d341b293197c7b7b0241e8.jpg)
_第138张图片](http://img.e-com-net.com/image/info8/0da0871194bb46aba35e41bd29ee0a06.jpg)
_第139张图片](http://img.e-com-net.com/image/info8/0fea9379ee774eb09838e79ee734c544.jpg)
_第140张图片](http://img.e-com-net.com/image/info8/ba0b19b6aac447a9839145f0c408854b.jpg)
_第141张图片](http://img.e-com-net.com/image/info8/133e840d6eac4aed9d153b11eba1bf96.jpg)
_第142张图片](http://img.e-com-net.com/image/info8/b936112b932e496dbccf3980e0f26480.jpg)
_第143张图片](http://img.e-com-net.com/image/info8/d0c44f957e6641df8e227c0befa2f716.jpg)
_第144张图片](http://img.e-com-net.com/image/info8/cce99f35ec424e7990cdb5cdce26b2fa.jpg)
_第145张图片](http://img.e-com-net.com/image/info8/979ecac980b74f6ab0baf70b0a4f0821.jpg)


_第151张图片](http://img.e-com-net.com/image/info8/ce29decc6c6a4d2e8144d56f0640f73c.jpg)
_第152张图片](http://img.e-com-net.com/image/info8/c22abe18163f43f89373ac605ecab8b1.jpg)
_第153张图片](http://img.e-com-net.com/image/info8/8c2789d519814c05a648db900fd996ac.jpg)
_第154张图片](http://img.e-com-net.com/image/info8/5aa708c69364419f88923fd65525ba35.jpg)
_第155张图片](http://img.e-com-net.com/image/info8/d0b5b8e9d15f4a309102058190feef4a.jpg)
_第156张图片](http://img.e-com-net.com/image/info8/bd72869236a2443195efad44716d67b7.jpg)
_第159张图片](http://img.e-com-net.com/image/info8/94aa032b56674e2da1c351fec9ec9788.jpg)
_第160张图片](http://img.e-com-net.com/image/info8/57c7b56d5cf5412585a60a46823ed053.jpg)
_第172张图片](http://img.e-com-net.com/image/info8/b7e3367e0bf34e35894436d733359398.jpg)
_第173张图片](http://img.e-com-net.com/image/info8/93b642ff29434cc1ad2f579a0020a62a.jpg)
_第174张图片](http://img.e-com-net.com/image/info8/eca0647eb6914370a48dbcfa486827cf.jpg)
_第175张图片](http://img.e-com-net.com/image/info8/c9110515cbb34c15b3fe785d44a07efd.jpg)
_第176张图片](http://img.e-com-net.com/image/info8/8adac2eb01564e168384072cf72cb4e2.jpg)
_第177张图片](http://img.e-com-net.com/image/info8/8a5d10ff5e384e3f99a730193c09f6a7.jpg)
_第178张图片](http://img.e-com-net.com/image/info8/3b3f402adbe240a59bc8d2d5259432e5.jpg)
_第179张图片](http://img.e-com-net.com/image/info8/dd418a965a514ea08d6f23b383585703.jpg)
_第180张图片](http://img.e-com-net.com/image/info8/8509d53e4e5f44f58eb058126366be27.jpg)
_第181张图片](http://img.e-com-net.com/image/info8/8c8fdcec7ce74709b36dc00fa957869e.jpg)
_第186张图片](http://img.e-com-net.com/image/info8/12e7808e376845a4b7da0312946fbd49.jpg)
_第193张图片](http://img.e-com-net.com/image/info8/046cde8a803b4bd0bb8af27cfd7e80d6.jpg)
_第195张图片](http://img.e-com-net.com/image/info8/0cab7959e6a147a386abfd364c66af5f.jpg)
_第196张图片](http://img.e-com-net.com/image/info8/abc5ee9165e94ce3aac8931590170a94.jpg)
_第197张图片](http://img.e-com-net.com/image/info8/bec75d736a924349915f1292f0a30ceb.jpg)
_第198张图片](http://img.e-com-net.com/image/info8/f3e73616c2174805b620c2a154a8e805.jpg)
_第202张图片](http://img.e-com-net.com/image/info8/65405028bcfc459cb0871921929a2141.jpg)
_第208张图片](http://img.e-com-net.com/image/info8/87fea89d569847ebb3bf21819ac6471c.jpg)
_第209张图片](http://img.e-com-net.com/image/info8/abbc7a07ac93435da0928ae8ba425e57.jpg)
_第210张图片](http://img.e-com-net.com/image/info8/1b6859dedf9044b1b4d479acb4e1f306.jpg)
_第211张图片](http://img.e-com-net.com/image/info8/c218a86e67ce42f2b5862fc4a336029a.jpg)
_第212张图片](http://img.e-com-net.com/image/info8/a95986ae999c456dbabd46d8bbd18132.jpg)
_第213张图片](http://img.e-com-net.com/image/info8/8c89d07db9a0411eb2a278869d15cf96.jpg)
_第214张图片](http://img.e-com-net.com/image/info8/fd5597480e63442eb9ed2daecd6e2481.jpg)
_第215张图片](http://img.e-com-net.com/image/info8/475ddb5af70545859d428f871c732efb.jpg)
_第221张图片](http://img.e-com-net.com/image/info8/0c96e6bfa90e4c7490c34fae4bf0f79d.jpg)
_第226张图片](http://img.e-com-net.com/image/info8/1ff247f68c8d49298c67e548112ad4df.jpg)
_第227张图片](http://img.e-com-net.com/image/info8/b6f4aca760784fbfa011011f22d57ec1.jpg)
_第228张图片](http://img.e-com-net.com/image/info8/578ce6243d004c9490c273880abd662a.jpg)
_第229张图片](http://img.e-com-net.com/image/info8/de55c1ba7837483380ce07fa3e993e7c.jpg)
_第230张图片](http://img.e-com-net.com/image/info8/0b1b9952b6284df78a6d8ffcc3ff2a5b.jpg)

_第231张图片](http://img.e-com-net.com/image/info8/892e329a5977469b8f6896945766c77e.jpg)
_第232张图片](http://img.e-com-net.com/image/info8/35dbdfeb12e744b88a9efc9ecf5768e2.jpg)
_第233张图片](http://img.e-com-net.com/image/info8/0f25f23f7872428094822ebb1318bee2.jpg)
_第234张图片](http://img.e-com-net.com/image/info8/016fb6400610409b9185e8f50e6f027c.jpg)
_第235张图片](http://img.e-com-net.com/image/info8/f35f6d6786d844e786aa7ecdd539c0f3.jpg)
_第237张图片](http://img.e-com-net.com/image/info8/425001922b224b5081ab7c66d036774b.jpg)
_第238张图片](http://img.e-com-net.com/image/info8/68a7abb654c84be7b56cd74c6dbcaca9.jpg)

_第242张图片](http://img.e-com-net.com/image/info8/7a9fd74669854cf58013ce7c4cd212f8.jpg)
_第244张图片](http://img.e-com-net.com/image/info8/382fc7ffdadd45a2a0aa24fac605603a.jpg)
_第245张图片](http://img.e-com-net.com/image/info8/bb7940cf9f4c4b01958ac315e38653c8.jpg)
_第246张图片](http://img.e-com-net.com/image/info8/ad928d3846d94b9e8a5e2b4c95d67677.jpg)
_第247张图片](http://img.e-com-net.com/image/info8/a137fc0c3b4040a3a2ab5e6f81c1f520.jpg)
_第248张图片](http://img.e-com-net.com/image/info8/fba8da494a724ba49bc520236a6e3b4c.jpg)
_第249张图片](http://img.e-com-net.com/image/info8/512d1da6ee6943f099f834c53e41a910.jpg)
_第250张图片](http://img.e-com-net.com/image/info8/1ac2cf92fe8743f38535655ebba73c81.jpg)
_第251张图片](http://img.e-com-net.com/image/info8/910db3d9a127499ea00768c5da8f27ef.jpg)
_第252张图片](http://img.e-com-net.com/image/info8/fbc5baf3f65f4738b73aaf9e33d769f9.jpg)
_第253张图片](http://img.e-com-net.com/image/info8/1005668d898d4db8928328ba9fb940d4.jpg)
_第254张图片](http://img.e-com-net.com/image/info8/4ad2deb39d7646ba862e7969014e79e4.jpg)
_第255张图片](http://img.e-com-net.com/image/info8/75b785964ab7489a81539cb9ebda1519.jpg)
_第259张图片](http://img.e-com-net.com/image/info8/901e7b90c96444a4819cddb1659c14ac.jpg)
_第260张图片](http://img.e-com-net.com/image/info8/ae2145dea5184270a93a294c8f95c433.jpg)
_第261张图片](http://img.e-com-net.com/image/info8/cbf609fc9a254255906fc1057ca834eb.jpg)
_第263张图片](http://img.e-com-net.com/image/info8/eba9df1520ab4fdcbee1957ecf6500b3.jpg)
_第264张图片](http://img.e-com-net.com/image/info8/1cfd057030af4b0780d1045db0b8c805.jpg)
_第265张图片](http://img.e-com-net.com/image/info8/a8051dbf2bf2405a9d42b05039993104.jpg)