万字长文搞懂MobileNetv1模型

MobileNetv1 论文详解

MobileNet 论文的主要贡献在于提出了一种深度可分离卷积架构（DW+PW 卷积），先通过理论证明这种架构比常规的卷积计算成本（Mult-Adds）更小，然后通过分类、检测等多种实验证明模型的有效性。（正经标题：MobileNet v1 论文详解。）
文章首发于 github 和 知乎。

1、相关工作

标准卷积

一个大小为 $h_1\times w_1$ 过滤器（2 维卷积核），沿着 feature map 的左上角移动到右下角，过滤器每移动一次，将过滤器参数矩阵和对应特征图 $h_1\times w_1\times c_1$ 大小的区域内的像素点相乘后累加得到一个值，又因为 feature map 的数量（通道数）为 $c_1$，所以我们需要一个 shape 为 $ (c_1, h_1, w_1)$ 的滤波器（ 3 维卷积核），将每个输入 featue map 对应输出像素点位置计算和的值相加，即得到输出 feature map 对应像素点的值。又因为输出 feature map 的数量为 $c_2$ 个，所以需要 $c_2$ 个滤波器。标准卷积抽象过程如下图所示。

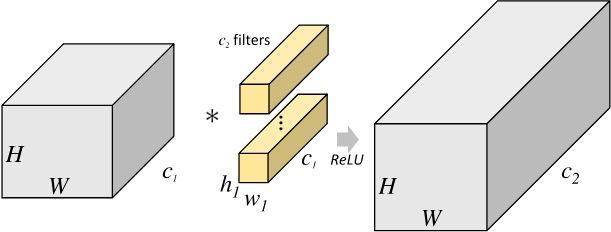
2D 卷积计算过程动态图如下，通过这张图能够更直观理解卷积核如何执行滑窗操作，又如何相加并输出 $c_2$ 个 feature map ，动态图来源 这里。

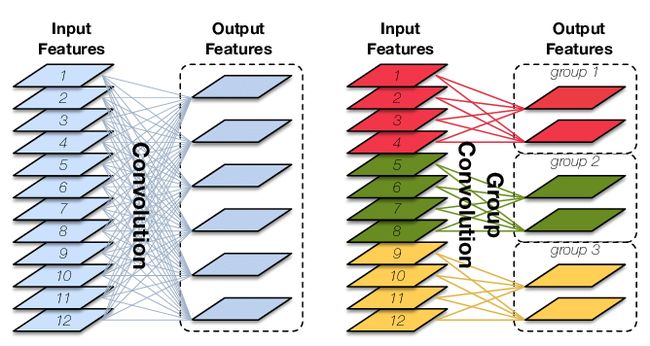
分组卷积

Group Convolution 分组卷积，最早见于 AlexNet。常规卷积与分组卷积的输入 feature map 与输出 feature map 的连接方式如下图所示，图片来自CondenseNet。

分组卷积的定义：对输入 feature map 进行分组，然后分组分别进行卷积。假设输入 feature map 的尺寸为 $H\times W\times c_1$，输出 feature map 数量为 $c_2$ 个，如果将输入 feature map 按通道分为 $g$ 组，则每组特征图的尺寸为 $H\times W\times \frac{c_1}{g}$，每组对应的滤波器（卷积核）的 尺寸 为 $h_1\times w_1\times \frac{c_1}{g}$，每组的滤波器数量为 $\frac{c_2}{g}$ 个，滤波器总数依然为 $c_2$ 个，即分组卷积的卷积核 shape 为 $(c_2,\frac{c_1}{g},h_1,w_1)$。每组的滤波器只与其同组的输入 map 进行卷积，每组输出特征图尺寸为 $H\times W\times \frac{c_2}{g}$，将 $g$ 组卷积后的结果进行拼接 (concatenate) 得到最终的得到最终尺寸为 $H\times W\times c_2$ 的输出特征图，其分组卷积过程如下图所示：

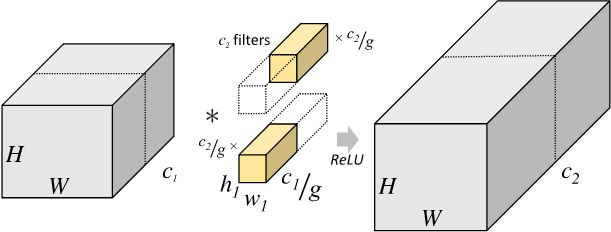
分组卷积的意义：分组卷积是现在网络结构设计的核心，它通过通道之间的稀疏连接（也就是只和同一个组内的特征连接）来降低计算复杂度。一方面，它允许我们使用更多的通道数来增加网络容量进而提升准确率，但另一方面随着通道数的增多也对带来更多的 $MAC$。针对 $1\times 1$ 的分组卷积，$MAC$ 和 $FLOPs$ 计算如下：

$$\begin{array}{rl}& MACC=H\times W\times 1\times 1\times \frac{c_1}{g}\frac{c_2}{g}\times g=\frac{hw{c}_1{c}_2}{g}\\ & \\ & FLOPs=2\times MACC\\ & \\ & Params=g\times \frac{c_2}{g}\times \frac{c_1}{g}\times 1\times 1+c_2=\frac{c_1{c}_2}{g}\\ & \\ & MAC=HW(c_1+c_2)+\frac{c_1{c}_2}{g}\\ & \end{array}$$

从以上公式可以得出分组卷积的参数量和计算量是标准卷积的 $\frac{1}{g}$ 的结论 ，但其实对分组卷积过程进行深入理解之后也可以直接得出以上结论。

分组卷积的深入理解：对于 $1\times 1$ 卷积，常规卷积输出的特征图上，每一个像素点是由输入特征图的 $c_1$ 个点计算得到，而分组卷积输出的特征图上，每一个像素点是由输入特征图的 $ \frac{c_1}{g}$个点得到（参考常规卷积计算过程）。卷积运算过程是线性的，自然，分组卷积的参数量和计算量是标准卷积的 $\frac{1}{g}$ 了。

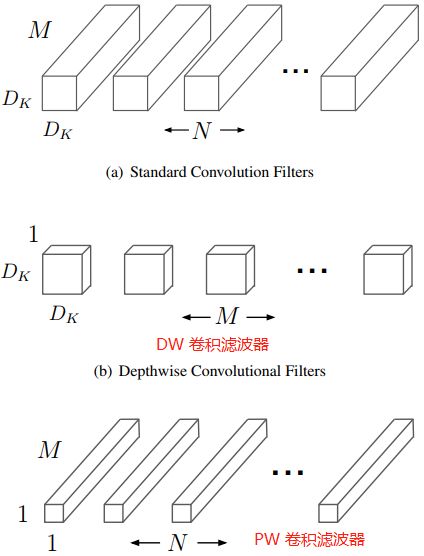
当分组卷积的分组数量 = 输入 feature map 数量 = 输出 feature map 数量，即 $g=c_1=c_2$，有 $c_1$ 个滤波器，且每个滤波器尺寸为 $1\times K\times K$ 时，Group Convolution 就成了 Depthwise Convolution（DW 卷积），DW 卷积的卷积核权重尺寸为 $(c_1,1,K,K)$。

常规卷积的卷积核权重 shape 都为（C_out, C_in, kernel_height, kernel_width），分组卷积的卷积核权重 shape 为（C_out, C_in/g, kernel_height, kernel_width），DW 卷积的卷积核权重 shape 为（C_in, 1, kernel_height, kernel_width）。

从 Inception module 到 depthwise separable convolutions

深度可分离卷积（depthwise separable convolutions）的提出最早来源于 Xception 论文，Xception 的论文中提到，对于卷积来说，卷积核可以看做一个三维的滤波器：通道维+空间维（Feature Map 的宽和高），常规的卷积操作其实就是实现通道相关性和空间相关性的联合映射。Inception 模块的背后存在这样的一种假设：卷积层通道间的相关性和空间相关性是可以退耦合（完全可分）的，将它们分开映射，能达到更好的效果（the fundamental hypothesis behind Inception is that cross-channel correlations and spatial correlations are sufficiently decoupled that it is preferable not to map them jointly.）。

引入深度可分离卷积的 Inception，称之为 Xception，其作为 Inception v3 的改进版，在 ImageNet 和 JFT 数据集上有一定的性能提升，但是参数量和速度并没有太大的变化，因为 Xception 的目的也不在于模型的压缩。深度可分离卷积的 Inception 模块如图 Figure 4 所示。

Figure 4 中的“极限” Inception 模块与本文的主角-深度可分离卷积模块相似，区别在于：深度可分离卷积先进行 channel-wise 的空间卷积，再进行 $1\times 1$ 的通道卷积，Figure 4 的 Inception 则相反；

2、MobileNets 结构

depthwise separable convolutions

MobileNets 是谷歌 2017 年提出的一种高效的移动端轻量化网络，其核心是深度可分离卷积。depthwise separable convolutions（深度可分离卷积） 的核心思想是将一个完整的卷积运算分解为两步进行，分别为 Depthwise Convolution（DW 卷积） 与 Pointwise Convolution（PW 卷积）。深度可分离卷积的计算步骤和滤波器尺寸如下所示。

Depthwise 卷积

注意本文 DW 和 PW 卷积计算量的计算与论文有所区别，本文的输出 Feature map 大小是 $D_G\times D_G$， 论文公式是$D_F\times D_F$。

不同于常规卷积操作， Depthwise Convolution 的一个卷积核只负责一个通道，一个通道只能被一个卷积核卷积（不同的通道采用不同的卷积核卷积），也就是输入通道、输出通道和分组数相同的特殊分组卷积，因此 Depthwise（DW）卷积不会改变输入特征图的通道数目。深度可分离卷积的 DW卷积步骤如下图：

DW 卷积的计算量 $MACC=M\times D_G^2\times D_K^2$

Pointwise 卷积

上述 Depthwise 卷积的问题在于它让每个卷积核单独对一个通道进行计算，但是各个通道的信息没有达到交换，从而在网络后续信息流动中会损失通道之间的信息，因此论文中就加入了 Pointwise 卷积操作，来进一步融合通道之间的信息。PW 卷积是一种特殊的常规卷积，卷积核的尺寸为 $1\times 1$。PW 卷积的过程如下图：

假设输入特征图大小为 $D_G\times D_G\times M$，输出特征图大小为 $D_G\times D_G\times N$，则滤波器尺寸为 $1\times 1\times M$，且一共有 $N$ 个滤波器。因此可计算得到 PW 卷积的计算量 $MACC=N\times M\times D_G^2$。

综上：Depthwise 和 Pointwise 卷积这两部分的计算量相加为 $MACC1=M\times D_G^2\times D_K^2+N\times M\times D_G^2$，而标准卷积的计算量 $MACC2=N\times D_G^2\times D_K^2\times M$。所以深度可分离卷积计算量于标准卷积计算量比值的计算公式如下。

$$\begin{array}{rl}\frac{DepthwiseSeparableConv}{StandardConv}& =\frac{M\times D_G^2(D_K^2+N)}{N\times D_G^2\times D_K^2\times M}\\ & \\ & =\frac{D_K^2+N}{D_K^2\times N}\\ & \\ & =\frac{1}{N}+\frac{1}{D_K^2}\\ & \end{array}$$

可以看到 Depthwise + Pointwise 卷积的计算量相较于标准卷积近乎减少了 $N$ 倍，$N$ 为输出特征图的通道数目，同理参数量也会减少很多。在达到相同目的（即对相邻元素以及通道之间信息进行计算）下， 深度可分离卷积能极大减少卷积计算量，因此大量移动端网络的 backbone 都采用了这种卷积结构，再加上模型蒸馏，剪枝，能让移动端更高效的推理。

深度可分离卷积的详细计算过程可参考 Depthwise卷积与Pointwise卷积。

2.2、网络结构

$3\times 3$ 的深度可分离卷积 Block 结构如下图所示：

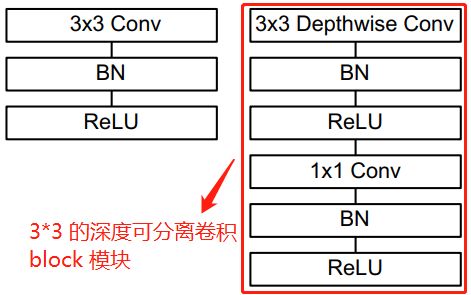
左边是带 bn 和 relu 的标准卷积层，右边是带 bn 和 relu 的深度可分离卷积层。
$3\times 3$ 的深度可分离卷积 Block 网络的 pytorch 代码如下：

class MobilnetV1Block(nn.Module):
    """Depthwise conv + Pointwise conv"""
    def __init__(self, in_channels, out_channels, stride=1):
        super(MobilnetV1Block, self).__init__()
        # dw conv kernel shape is (in_channels, 1, ksize, ksize)
        self.dw = nn.Conv2d(in_channels, in_channels, kernel_size=3,stride=stride,padding=1, groups=in_channels, bias=False)
        self.bn1 = nn.BatchNorm2d(in_channels)
        self.pw = nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=1, padding=0, bias=False)
        self.bn2 = nn.BatchNorm2d(out_channels)
    
    def forward(self, x):
        out1 = F.relu(self.bn1(self.dw(x)))
        out2 = F.relu(self.bn2(self.pw(out1)))
        return out2

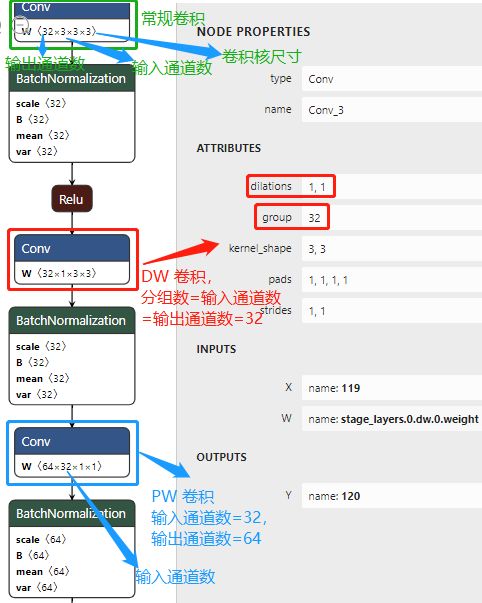
MobileNet v1 的 pytorch 模型导出为 onnx 模型后，深度可分离卷积 block 结构图如下图所示。

仅用 MobileNets 的 Mult-Adds（乘加操作）次数更少来定义高性能网络是不够的，确保这些操作能够有效实施也很重要。例如非结构化稀疏矩阵运算（unstructured sparse matrix operations）通常并不会比密集矩阵运算（dense matrix operations）快，除非是非常高的稀疏度。

这句话是不是和 shufflenet v2 的观点一致，即不能仅仅以 FLOPs 计算量来表现网络的运行速度，除非是同一种网络架构。

MobileNet 模型结构将几乎所有计算都放入密集的 1×1 卷积中（dense 1 × 1 convolutions），卷积计算可以通过高度优化的通用矩阵乘法（GEMM）函数来实现。 卷积通常由 GEMM 实现，但需要在内存中进行名为 im2col 的初始重新排序，然后才映射到 GEMM。 caffe 框架就是使用这种方法实现卷积计算。 1×1 卷积不需要在内存中进行重新排序，可以直接使用 GEMM（最优化的数值线性代数算法之一）来实现。

如表 2 所示，MobileNet 模型的 1x1 卷积占据了 95% 的计算量和 75% 的参数，剩下的参数几乎都在全连接层中， 3x3 的 DW 卷积核常规卷积占据了很少的计算量（Mult-Adds）和参数。

2.3、宽度乘系数-更小的模型

尽管基本的 MobileNet 体系结构已经很小且网络延迟 latency 很低，但很多情况下特定用例或应用可能要求模型变得更小，更快。为了构建这些更小且计算成本更低的模型，我们引入了一个非常简单的参数 $\alpha$，称为 width 乘数。宽度乘数 $\alpha$ 的作用是使每一层的网络均匀变薄。对于给定的层和宽度乘数 $\alpha$，输入通道的数量变为 $\alpha M$，而输出通道的数量 $N$ 变为 $\alpha N$。具有宽度乘数 $\alpha$ 的深度可分离卷积（其它参数和上文一致）的计算成本为：

$$\alpha M\times D_G^2\times D_K^2+\alpha N\times \alpha M\times D_G^2$$

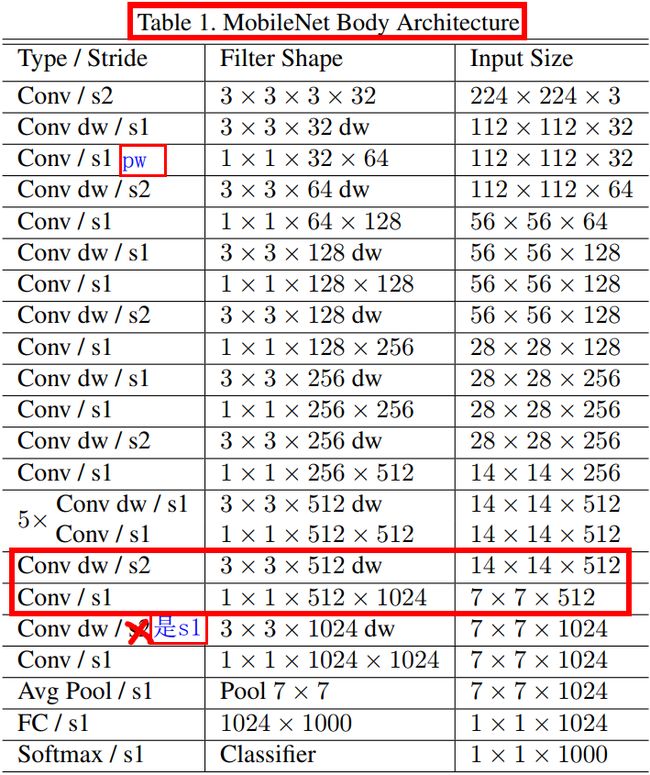
其中 $\alpha \in (0,1]$，典型值设置为 1、0.75、0.5 和 0.25。$\alpha =1$ 是基准 MobileNet 模型，$\alpha <1$ 是缩小版的 MobileNets。宽度乘数的作用是将计算量和参数数量大约减少 ${\alpha }^2$ 倍，从而降低了网络计算成本（ computational cost of a neural network）。 宽度乘数可以应用于任何模型结构，以定义新的较小模型，且具有合理的准确性、网络延迟 latency 和模型大小之间的权衡。 它用于定义新的精简结构，需要从头开始进行训练模型。基准 MobileNet 模型的整体结构定义如表 1 所示。

2.4、分辨率乘系数-减少表示

减少模型计算成本的的第二个超参数（hyper-parameter）是分辨率因子 $\rho$，论文将其应用于输入图像，则网络的每一层 feature map 大小也要乘以 $\rho$。实际上，论文通过设置输入分辨率来隐式设置 $\rho$。
将网络核心层的计算成本表示为具有宽度乘数 $\alpha$ 和分辨率乘数 $\rho$ 的深度可分离卷积的公式如下：
$$\alpha M\times \rho D_G^2\times D_K^2+\alpha N\times \alpha M\times \rho D_G^2$$
其中 $\rho \in (0,1]$，通常是隐式设置的，因此网络的输入分辨率为 224、192、160 或 128。$\rho =1$ 时是基准(baseline) MobilNet，$\rho <1$ 时缩小版 MobileNets。分辨率乘数的作用是将计算量减少 ${\rho }^2$。

2.5、模型结构总结

• 整个网络不算平均池化层与 softmax 层，且将 DW 卷积和 PW 卷积计为单独的一层，则 MobileNet 有 28 层网络。+ 在整个网络结构中步长为2的卷积较有特点，卷积的同时充当下采样的功能；
• 第一层之后的 26 层都为深度可分离卷积的重复卷积操作，分为 4 个卷积 stage；
• 每一个卷积层（含常规卷积、深度卷积、逐点卷积）之后都紧跟着批规范化和 ReLU 激活函数；
• 最后一层全连接层不使用激活函数。

3、实验

作者分别进行了 Stanford Dogs dataset 数据集上的细粒度识别、大规模地理分类、人脸属性分类、COCO 数据集上目标检测的实验，来证明与 Inception V3、GoogleNet、VGG16 等 backbone 相比，MobilNets 模型可以在计算量（Mult-Adds）数 10 被下降的情况下，但是精度却几乎不变。

4、结论

论文提出了一种基于深度可分离卷积的新模型架构，称为 MobileNets。 在相关工作章节中，作者首先调查了一些让模型更有效的重要设计原则，然后，演示了如何通过宽度乘数和分辨率乘数来构建更小，更快的 MobileNet，通过权衡合理的精度以减少模型大小和延迟。 然后，我们将不同的 MobileNets 与流行的模型进行了比较，这些模型展示了出色的尺寸，速度和准确性特性。 最后，论文演示了 MobileNet 在应用于各种任务时的有效性。

5、基准模型代码

自己复现的基准 MobileNet v1 代模型 pytorch 代码如下：

import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision.models as models
from torch import flatten

class MobilnetV1Block(nn.Module):
    """Depthwise conv + Pointwise conv"""

    def __init__(self, in_channels, out_channels, stride=1):
        super(MobilnetV1Block, self).__init__()
        # dw conv kernel shape is (in_channels, 1, ksize, ksize)
        self.dw = nn.Sequential(
            nn.Conv2d(in_channels, 64, kernel_size=3,
                      stride=stride, padding=1, groups=4, bias=False),
            nn.BatchNorm2d(in_channels),
            nn.ReLU(inplace=True)
        )
        # print(self.dw[0].weight.shape)  # print dw conv kernel shape
        self.pw = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, kernel_size=1,
                      stride=1, padding=0, bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU(inplace=True)
        )

    def forward(self, x):
        x = self.dw(x)
        x = self.pw(x)
        return x


def convbn_relu(in_channels, out_channels, stride=2):
    return nn.Sequential(nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=stride,
                                   padding=1, bias=False),
                         nn.BatchNorm2d(out_channels),
                         nn.ReLU(inplace=True))


class MobileNetV1(nn.Module):
    # (32, 64, 1) means MobilnetV1Block in_channnels is 32, out_channels is 64, no change in map size.
    stage_cfg = [(32, 64, 1), 
           (64, 128, 2), (128, 128, 1),     # stage1 conv
           (128, 256, 2), (256, 256, 1),    # stage2 conv
           (256, 512, 2), (512, 512, 1), (512, 512, 1), (512, 512, 1), (512, 512, 1), (512, 512, 1), # stage3 conv
           (512, 1024, 2), (1024, 1024, 1)  # stage4 conv
    ]
    def __init__(self, num_classes=1000):
        super(MobileNetV1, self).__init__()
        self.first_conv = convbn_relu(3, 32, 2)  # Input image size reduced by half
        self.stage_layers = self._make_layers(in_channels=32)
        self.linear = nn.Linear(1024, num_classes)  # 全连接层

    def _make_layers(self, in_channels):
        layers = []
        for x in self.stage_cfg:
            in_channels = x[0]
            out_channels = x[1]
            stride = x[2]
            layers.append(MobilnetV1Block(in_channels, out_channels, stride))
            in_channels = out_channels
        return nn.Sequential(*layers)

    def forward(self, x):
        """Feature map shape(h、w) is 224 -> 112 -> 56 -> 28 -> 14 -> 7 -> 1"""
        x = self.first_conv(x)
        x = self.stage_layers(x)

        x = F.avg_pool2d(x, 7)  # x shape is 7*7
        x = flatten(x, 1)       # x = x.view(x.size(0), -1)
        x = self.linear(x)

        return x


if __name__ == "__main__":
    model = MobileNetV1()
    model.eval()                  # set the model to inference mode
    input_data = torch.rand(1, 3, 224, 224)
    outputs = model(input_data)
    print("Model output size is", outputs.size())

程序运行结果如下：

Model output size is torch.Size([1, 1000])

参考资料

1. Group Convolution分组卷积，以及Depthwise Convolution和Global Depthwise Convolution
2. 理解分组卷积和深度可分离卷积如何降低参数量
3. 深度可分离卷积（Xception 与 MobileNet 的点滴）
4. MobileNetV1代码实现
5. Depthwise卷积与Pointwise卷积
6. 【CNN结构设计】深入理解深度可分离卷积