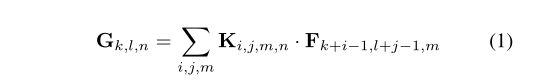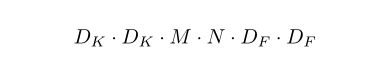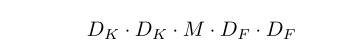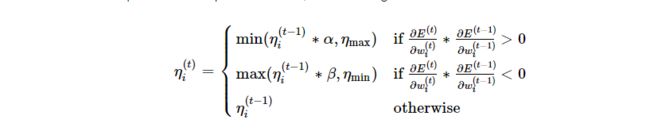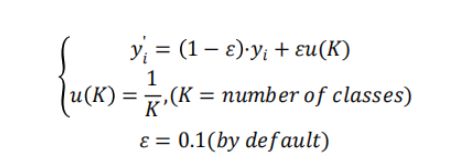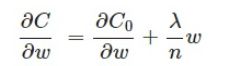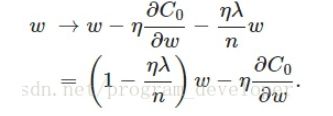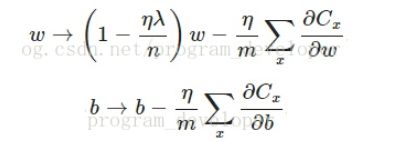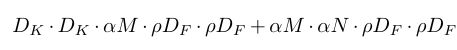【文献笔记】【精读】MobileNet V1
文章目录
- 1 论文结构
- 2 研究的问题
- 3 文献综述
-
- 3.1 当前(2017)已有的DNN的问题
- 3.2 当前已有的网络轻量化的方法
- 4 MobileNet 简介
-
- 4.1 本网络创新点
- 4.2 本网络优点
- 5 MobileNet 详解
-
- 5.1 the core layers: depthwise separable filters
- 5.2 计算代价(computational cost)是怎么算出来的?
-
-
- 5.2.1 一个标准卷积层的计算过程到底是怎样的
- 5.2.2 depthwise separable convolution 与 standard convolution 在计算上有什么不同?
- 5.2.3 做卷积时乘法次数如何计算
-
- 5.3 阶段性总结
- 5.4 MobileNet 结构
-
- 5.4.1 BN 和 ReLU 是什么
- 5.4.2 pooling
-
- average pooling
- max pooling
- 5.4.3 MobileNet 具体结构
- 5.5 MobileNet 训练方法
-
- 5.5.1 RMSprop
-
- rprop
- RMSprop
- Adagrad
- 5.5.2 Inception-V3
- 5.5.3 异步梯度下降法
-
- 先科普以下梯度下降的发展历史
- 数据并行、模型并行与计算并行
- 同步算法与异步算法
- 5.5.4 DNN中术语解释
-
- backbone
- head
- neck
- bottleneck
- GAP
- Embedding
- pretext task & downstream task
- warm up
- end to end
- 5.5.5 label smoothing
- 5.5.6 weight decay
- 5.6 超参数 α 和 ρ
-
- 5.6.1 Width Multiplier α
-
- α 的目的
- 5.6.2 Resolution Multiplier ρ
- 6 数据图解析
-
-
-
- 加上 α 和 ρ 后的计算量和参数变化
- 各种 MobileNet 大比拼
- MobileNet 与其他网络结构大比拼
-
-
- 7 知识点补充
-
- 7.1 什么叫蒸馏
开头提示
本笔记适合于刚刚接触深度学习,想通过精读一篇文章来达到入门目的的人
1 论文结构
-
section 1:网络介绍
-
section 2:回顾先前的相关工作
-
section 3:介绍MobileNet的体系结构以及两个超参数(宽度乘法器、分辨率乘法器),以定义Mobile Net
-
section 4: 介绍本网络在ImageNet上的实验以及大量的应用场景
-
section 5: 总结
2 研究的问题
设计一个在优化延迟的基础上还兼顾了网络的轻量化,用于移动端和侵入式端的视觉任务的DNN
3 文献综述
3.1 当前(2017)已有的DNN的问题
-
为了提高准确率越来越深、越来越复杂,但是其为了提高准确率而作出的进步并不一定使网络在尺寸和速度方面更加有效
-
在真实的应用场景中,识别任务需要考虑两个问题
- 及时性(速度)
- 算力有限(尺寸)
当前很多轻量级网络仅仅专注于小型网络而忽略了网络的运行速度
3.2 当前已有的网络轻量化的方法
-
直接训练更小的网络
- depthwise separable convolutions: a form of facorized convolutions
- flattened networks
- factorized networks
- Xception network: scale up depthwise separable filters
- Squeezenet: uses a bottleneck approach to design a very small network
- sructured transform networks
- deep fried convnets
-
shrinking / factorizing(分解) / compressing 预训练网络
-
distillation(蒸馏),即用一个更大的网络来teach一个我们要的较小的网络
-
low bit network(低比特网络)
其中,MobileNet借鉴了蒸馏的方法
4 MobileNet 简介
4.1 本网络创新点
-
深度可分离卷积 depthwise seperable convolutions
-
两个全局超参数,用来权衡延时与准确率,网络使用者可以通过调节这两个参数来选择适用于具体任务的网络尺寸
4.2 本网络优点
在优化延迟的基础上还兼顾了网络的轻量化,非常适合移动端和嵌入式;开发者可以根据具体任务的资源限制(时延、尺寸)来定制轻量级网络
5 MobileNet 详解
5.1 the core layers: depthwise separable filters
depthwise separable convolutions 本质是一种可分解卷积,它将一个标准的卷积分解为一个**(1)深度卷积**(depthwise convolution)和一个1*1的被称为**(2)点卷积**(pointwise convolution)的卷积核
(1)深度卷积:对每一个图像输入通道(channel)都应用一个单个的filter
(2)点卷积:应用1*1的卷积来组合深度卷积的输出
综上,一个标准卷积 在一个步骤中 被分为两层,一层用于过滤,一层用于合并。既过滤输入,又把输入组合成一组新的输出
这种分解方法大大减少了计算量和模型尺寸
u1s1,这公式看不懂
Dk·Dk是卷积核大小,DF·DF是feature map的大小(输入/输出中每一个channel的大小),M是输入通道数,N是输出通道数。
对于一个标准卷积来说, input feature map的shape为DF·DF·M,output feature map的shape为 DF·DF·N
以上是标准卷积的计算代价,而MobileNet最大的创新就是使用将标准卷积分解,使其计算代价大大减小
深度可分离卷积是MobileNet的第一步,它被用于打破输出通道数量以及卷积核大小之间的相互作用
相比标准卷积的计算代价已经大大减小了,但是经过了depthwise只是将 input 的各个 channel 独立用filter卷积了一遍,还不是一个最终的完整的output feature map,所以我们需要一个额外的 pointwise convolution ,即一个1*1的卷积来将这些各自独立的特征线性连接起来变成一个 feature map。
加上 pointwise convolution 之后整个两层的 depthwise separable convolutions的计算代价如下所示:
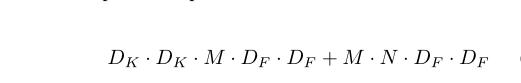
将 depthwise separable convolutions 的计算代价除以 standard convolution 的计算代价,就可以知道计算代价减小了多少:

5.2 计算代价(computational cost)是怎么算出来的?
5.2.1 一个标准卷积层的计算过程到底是怎样的
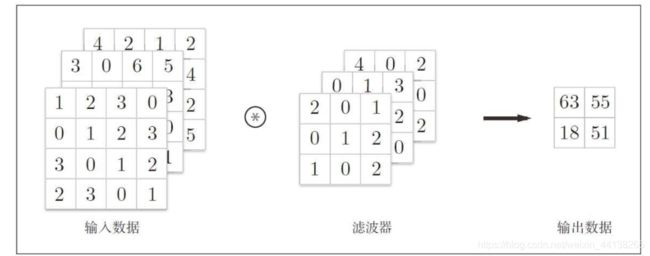
在图像处理任务中,我们进行的一般都是三维的卷积计算,一般 input 都可以表示为一个三维的张量(width,height,depth),其中 width*height 表示一张图片的大小,即横向纵向都有几个像素点,而 depth 则表示 通道(channel)数量,对于一张 RGB 格式的图片来说,depth就是3,分别表示R、G、B三原色。
综上,在MobileNet中,input 为 DF·DF·M,那么 DF·DF 就是 width*height,表示图片的大小;M 就是 depth,即 channels 的数量。
下面再来看卷积核的尺寸,在神经网络的卷积计算中,卷积核的 depth 必须和 input 的 depth 相同,所以 单个卷积核的 shape 为 DK·DK·M。DK自然就是单个卷积核的 width 和 height(所谓卷积核,就是矩阵)
论文中说卷积核的 size 为 DK·DK·M·N,N 就是这一层中卷积核的数量
关于输入的 shape 解释,可参考如下文章:
Understanding Input Output shapes in Convolution Neural Network | Keras
最后,output feature map 的 shape 应该如何得到?
那么,其实在 depth 相同的情况下,input feature map 与 单个卷积核做卷积也就可以看作是二维矩阵的卷积运算的叠加。当卷积核窗口在输入图像上滑动时,能够一次在其三个色彩通道上同时进行卷积操作,并且最终将三个 channel 对应位相加得到计算结果,即一个二维的矩阵。
那么 output feature map 的 width 和 height,即 DG,就可以由 (DF-DK)/stride+1 计算得出。
而 output feature map 的 depth,就是卷积核的个数N,那么其最终的 shape 就是 DG·DG·N
CNN中卷积计算的具体过程可见此博客:
机器学习入门(15)— 全连接层与卷积层的区别、卷积神经网络结构、卷积运算、填充、卷积步幅、三维数据卷积、多维卷积核运算以及批处理
综上,我们可以得到在图像处理任务中 output feature map 的 shape 与哪些因素有关?
- 输入图像的边长
- 卷积核的边长
- 卷积核在图像上滑动的步长
- 卷积核数量
一个标准卷积的运算过程可概括如下:
对于一个卷积层来说,假设 input 的 shape 是 DF·DF·M , 单个卷积核的 shape 是 DK·DK·M(DK必须小于DF,且卷积核的深度必须等于输入的通道数),那么单个卷积核(三维矩阵)和输入(也是三维矩阵)的卷积运算就是这样的:因为卷积核和输入的深度都相同,所以它们在每个通道上都进行二维的矩阵卷积运算,算完后得到 M 个二维矩阵,这些二维矩阵的边长为DG(DG = (DF-DK)/ stride +1),然后这M个二维矩阵各位对应相加,就得到一个ouput(二维矩阵),那么 N 个卷积核一共就产生 N 个output ,这 N 个 output 组合在一起就是最终的 大小为DG·DG·N 的 output feature map
5.2.2 depthwise separable convolution 与 standard convolution 在计算上有什么不同?
如果不了解 standard convolution的计算过程的话先看 5.2.1
standard convolution 的单个卷积核与 input 之间做的是三维的运算,每一层都有 N 个卷积核,而每一个DK·DK·M 的卷积核都要与整个 DF·DF·M 的输入做一次卷积运算
depthwise separable convolution有两层,我们将 depthwise convolution 和 pointwise convolution 分开讨论呢
在 standard convolution 中,N 可以看作是一个我们用来控制 output feature map 深度的参数,而在 depthwise convolution 中暂时先不考虑这个 N。
在 depthwise convolution 中,每一个卷积核的深度不再与 input 的通道数相等,而是固定为1,那么一个卷积核就是一个二维矩阵 DK·DK;而每一个卷积核也不再与完整的 input 作卷积运算,而是 由 M 个卷积核分别与 input 的 M 个通道作卷积运算,也就是作 M个 二维矩阵之间的卷积运算。
最后 depthwise convolution 输出的 shape 为 DG·DG·M
standard convolution 与 depthwise convolution 的区别见下图:
做完 depthwise convolution 后并没有结束,因为其只是在独立 filter 各个channel,最后得到的结果是 M 个独立的二维矩阵,互相之间没有联系,还不能说是一个图像。在 standard convolution 中卷积核的每一层与 input 的每一个channel 卷积后得到的 M 个二维矩阵会叠加在一起形成一个新的特征矩阵,而这份连接 M 个二维矩阵的工作在 depthwise separable convolution 中由 pointwise convolution 完成。
那么 pointwise convolution 是如何工作的呢?它由 N 个 1·1·M 的卷积核组成。它就像是 DG·DG·M 的输入(depthwise convolution的输出)与 N个1·1·M 的卷积核之间做了一次 standard convolution。
下图对比了在 MobileNet 中 standard convolution 与 depthwise separable convolution 的不同:

5.2.3 做卷积时乘法次数如何计算
所谓计算代价(computational cost),即在这一层中所作乘法的次数,加法不算
先算 standard convolution 中的乘法次数,一个 DF·DF 的二维矩阵与一个 DK·DK的二维矩阵相卷积,需要作 DG·DG·DK·DK 次乘法运算;input 的 channel 数量为 M,那么单个 DK·DK·M 的卷积核与 DF·DF·M 的 input 作一次卷积就需要在 M 个channel 上分别进行 DG·DG·DK·DK 次计算,那么单个卷积核卷积一次就需要作 DG·DG·DK·DK·M 次乘法计算,总共有 N 个卷积核,那么 standard convolution 的 计算代价就是 DG·DG·DK·DK·M·N
(在论文中假设 DG = DF,故得到的计算代价为 DF·DF·DK·DK·M·N)
接着计算 depthwise convolution 所需的乘法次数,一个 DK·DK 的卷积核和一个 DF·DF的 channel 相卷积,需要作 DG·DG·DK·DK次乘法运算;channel和卷积核是一一对应的,数量也都相等,都是 M,因此做一次 depthwise convolution 的计算代价就是 DF·DF·DK·DK·M (DF = DG)
再计算 pointwise convolution 所需的乘法次数,它可以看作是 DG·DG·M 的输入与 1·1·M 的卷积核之间作 standard convolution, 那么其计算代价就是 DF·DF·1·1·M·N (DG = DF)
最后,将 depthwise convolution 与 pointwise convolution 的计算代价相加就得到 depthwise separable convolution的计算代价,为 DF·DF·DK·DK·M + DF·DF·M·N
5.3 阶段性总结
depthwise separable convolutions 由 depthwise convolutions 和 pointwise convolutions 这两层网络构成,其目的就是大量减少计算代价。另外每一层都使用 batchnorm 和 ReLU 作为激活函数
5.4 MobileNet 结构
5.4.1 BN 和 ReLU 是什么
根据 Figure3,MobileNet 中每一个 layer 结束都要跟一个 BN 和 一个ReLU
BN 即 Batch Normalization, 是 normalization 这种 trick 的开山之作,用来防止模型在训练集上过拟合。其利用网络训练时一个 mini-batch 的数据来计算该神经元的均值和方差,并根据算出的均值和方差来调整这个神经元的值
x = ( x - x.mean() ) / x.std()
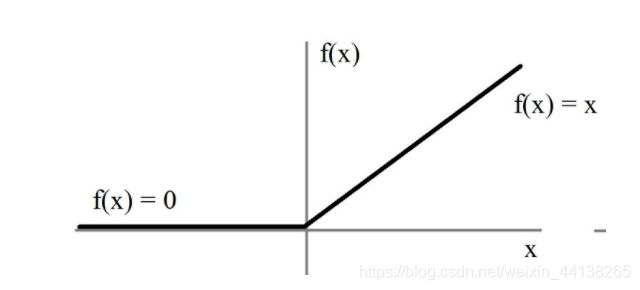
ReLu 激活函数:
x = max(x, 0)
5.4.2 pooling
第一层和深度卷积层使用 strided convolution 来降采样
就是把 stride 加大,减小输出的 spatial dimensions
降采样 (down sampling) 是为了解决输出特征图对于输入中特征位置敏感的问题。降采样能让输出特征图在输入图像中的特征位置改变时变得更加稳定。
池化层(pooling layers)也是一种降采样的方法。
pooling 分为 average pooling 和 max pooling
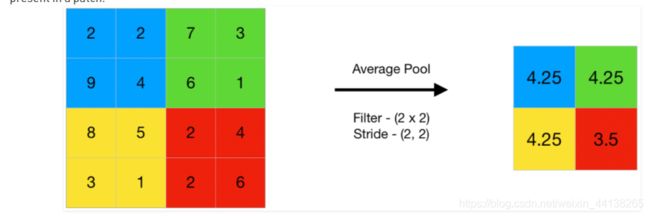
average pooling
average pooling 计算 filter 覆盖范围内的元素的平均值
在 pooling 中把一个 filter 覆盖的范围称为一个 patch
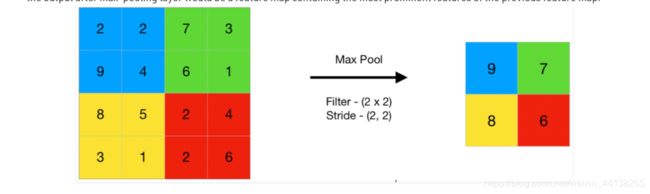
max pooling
max pooling 就是在每个 patch 中选出一个最大的元素,因此 max-pooling layer 的输出是输入特征图最显著的特征
5.4.3 MobileNet 具体结构
对于一个网络来说,仅仅是计算代价小还不够,还得合理规划网络的结构来使较小的计算代价充分发挥作用
如果将 depthwise convolution 和 pointwise convolution 分别看作独立的 layer,那么 MobileNet 一共有28层
一般在卷积层中作卷积运算时都会加上 padding, 即在二维矩阵旁边加0
加上 padding 后输出的 saptial dimensions 计算如下:

MobileNet Body Architecture 如下:
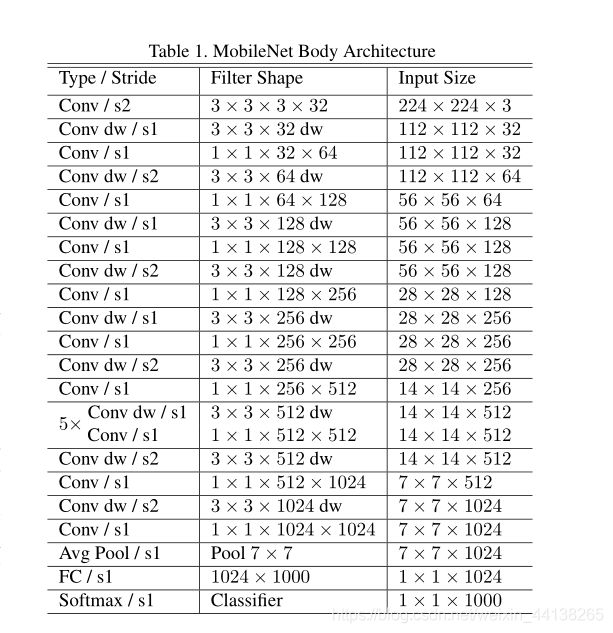
fully connected layer:每一个神经元都与上一层中的每一个神经元相连接
convolutional layer: 每一个神经元只与上一层中的部分神经元相连接
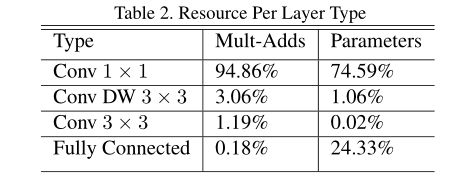
可以看到主要的计算量和参数都被放在了 pointwise convolution 中,因为在在计算此卷积时可以使用 高度优化的一般矩阵乘法(GEMM)函数。
全连接层和卷积层基本都是通过GEMM来实现的
GEMM 是最厉害的数值线性代数算法之一,但是 GEMM 美中不足的一点是为了将卷积映射到 GEMM,需要在内存中进行初始重新排序(称为 im2col)。
而在 pointwise convolution 中,1*1 的卷积不需要这种内存重排序,可以直接调用 GEMM 进行计算。
MobileNet中的资源分布(乘法次数 参数量)如下所示:
5.5 MobileNet 训练方法
论文中这么说:
“MoileNet 的模型在 tensorflow 中使用 RMSprop 进行训练,采用 类似于** Inception V3** 的异步梯度下降。”
“因为小模型不容易出现过拟合,所以 MobileNet 使用较少的正则化和数据增强技术”
“在训练 MobileNet 时作者没有使用 side heads 或者 label smoothing,并且通过 limiting the size of small crops that are used in large Inception training(没看懂,翻不出来)额外减少了扭曲图像的数量”
“因为深度卷积层的很少,所以不要在深度卷积层上使用 weight decay(L2 regularization),如果要用的话,也只能加一点点”
针对这句话有以下几个疑问:
- RMSprop 是什么东西?
- Inception V3 是什么东西?
- 异步梯度下降是什么?和普通梯度下降相比有什么区别?
- 什么是 side heads
- 什么是 label smoothing
- 什么是 weight decay
5.5.1 RMSprop
RMSprop 是一种基于梯度的优化算法,应用于神经网络中,属于自适应学习率方法(adaptive learning rate)。RMSprop被作为一种小批量(mini-batch)学习的随机技术在发展。它可以解决梯度消失或梯度爆炸问题。
RMSprop 如何解决梯度爆炸或梯度消失:使用梯度平方的均值来标准化梯度。这种标准化平衡了 step size(即学习率),在梯度很大的时候可以减小学习率以避免梯度爆炸,在梯度很小的时候可以增加学习率以避免梯度消失。
对于普通的梯度下降来说,学习率作为一个超参数是不变的,但是 RMSprop 的学习率是会随着时间变化的。
我们可以从两个方面来理解 RMSprop:
- 将其看作是 rprop 算法在小批量学习中的自适应研究(这也是开发此算法的初衷)
- 观察其与 Adagrad 的相似之处,并且 RMSprop 可以解决 Adagrad 中学习率急剧减少的问题。
rprop
在深入了解 RMSprop 之前,先了解以下 rprop,这是一种用于 full-batch optimization 的算法,可以动态调整学习过程中的学习率。
rprop 试图解决梯度大幅度变化的问题,因为有些梯度很小而有些梯度很大,所以想找一个具有普适性的单一的学习率就很困难。如果我们使用 full-batch learning 我们就可以通过仅使用梯度符号(the sign of the gradient)(梯度符号就是梯度的正负号)来解决这个问题。
权重调整的公示如下:
其中,sgn是符号函数,梯度大于0时,其值为1,梯度小于0时,其值为-1。
普通的梯度下降即使用了梯度的符号,又使用了梯度的幅度
在普通的梯度下降中,学习率 n 是不变的,在 rprop 算法中,n 随时间变化
RMSprop 为每个权重都单独调整学习率,以加速学习率向我们需要的方向(local minima 的方向)快速前进。
那么如何为权重调整学习率呢?
- 首先,我们查看这个权重最后两个梯度的符号(这个权重的数值肯定是时刻变化的)
- 如果这两个梯度符号相同,那么说明我们正在向着正确的方向前进,那么我们就以一定倍数放大学习率(比如 原学习率·1.2);如果这两个梯度不相等,那么说明我们之前的学习率太大了,都跳过 local minima 了,那么我们就应该以一定倍数减小学习率(比如 原学习率·0.5)
- 学习率的调整不是无限的,我们需要将学习率限制在两个特定的值之间,这两个值取决于自己的业务需求以及数据集,比较好的默认值为 50 和 百万分之一。
- 按照以上的规则,我们就可以更新权重了。
以上是 rprop 算法的一种简单形式,它还可以有其他的规则,可以由使用者视情况定义。
RMSprop
在数据集很大且需要小批量学习(mini-batchs)的情况下,rprop 就会不起作用。为什么呢?因为在这种情况下它违背了随机梯度下降的核心理念,那就是当学习率足够小时,它将连续的小批次的梯度给平均了。
举个例子,当连续的9个小批次的梯度都是0.1,而第10个小批次的梯度为-0.9时,我们期待的这10个小批次的梯度互相抵消变成0,但是当我们使用 rprop 时,我们增加了权重好多次之后才减小权重一次,
因为我们是仅仅通过梯度符号来调整学习率,因此只要梯度符号相同,一个幅值很大的梯度与一个幅值很小的梯度对于权重的影响是相同的。当在 full-batch 的情况下,一个 epoch 就只有一次迭代,即所有训练集都被送入网络训练,这样子算出的梯度是这个训练集真正的梯度(true gradient);但是在 mini-batchs 的情况下,一个 batch 只占训练集的一部分(每次 batch 训练后都会产生新一轮权重),因此每个 mini-batch 训练后的梯度并不是训练集真正的梯度。
在普通梯度下降中,因为学习率相同,所以 mini-batchs 的梯度差异会被抵消,如下所示:
等于是用 mini-batchs 的梯度的和来作为训练集梯度的估值。如果前4个 mini-batch 产生的梯度为 0.1, 第五个 mini-batch 产生的梯度为 -0.4,那么总的梯度变化就是0,很科学。
但是上述情况在 rprop 算法中就不一样了。因为在 prop 中学习率是每更新一个 mini-batch 就变化一次的,而且学习率在增大了四次后才会减小一次,那么最后的权重结果显然会变成一个更大的值,这就使 prop 算法变得不稳定,当 epoch 很大时(rprop需要很大的epoch来不断更新权重),效果就会变得差。
为了解决这个问题,RMSprop 就诞生了。其核心思想是在计算权重时,让学习率除以梯度的平方的滑动平均值(DSP中的概念)以进行变化,而不是向 rprop 那样根据两次梯度的符号是否相等来变化,这样学习率的变化就会根据梯度的幅度大小进行变化。公示如下:
其中,E(g^2) 为梯度的平方的滑动平均值;dC/dw 是权重相对于代价函数的梯度,即g;n 是学习率;beta 是滑动平均参数(一个很好的默认值为0.9)
损失函数与代价函数不一样
损失函数主要指的是对于单个样本的损失或误差;
代价函数表示多样本同时输入模型的时候总体的误差——每个样本误差的和然后取平均值。
当梯度幅度变大时,学习率就会变小,当梯度幅度变小时,学习率就会变大
rprop 算法只考虑梯度的符号,不考虑梯度的幅度;而 RMSprop 同时考虑了符号和幅度。
Adagrad
Adagrad 类似于 RMSprop,不同的地方在于RMSprop 更新学习率是通过除以梯度平方的滑动平均值,而 Adagrad 是除以梯度平方的历史总和。
Adagrad的代码如下
grads_squared = 0
for _ in num_iterations:
dw = compute_gradient(x, y)
grad_squared += dw * dw
w = w - (lr / np.sqrt(grad_squared)) * dw
如果梯度的幅度不断增大,那么学习率就会不断减小,如果梯度的幅度不断减小,那么学习率就会不断增大。在凸函数中,这很有道理,但是在非凸函数中,这样做很容易被困在 saddle point 中。
RMSprop 把累加变成滑动平均,可以缓解这个问题。
5.5.2 Inception-V3
和 MobileNet 一样,Inception-V3 也是一种神经网络结构,不多赘述
5.5.3 异步梯度下降法
先科普以下梯度下降的发展历史
普通的梯度下降使用全部数据计算得到全梯度,而随机梯度下降使用有放回抽样随机抽取的一个样本的梯度替代全梯度,大大减少了计算量,也大大节省了计算机内部的存储空间,不必一次加载全部数据集到内存中。而且当数据量很大的时候,随机梯度下降法总体计算复杂度要低。
不过随机梯度下降算法的收敛速率更慢,主要原因是随机梯度下降的梯度是全梯度的无偏估计,存在一定的方差,引入了不确定性,最终导致收敛速率下降。
随机梯度下降算法的一个推广是小批量(mini-batch)随机梯度下降法,也就是每次迭代时随机抽取多个样本(不是全部,比如取32个)来计算梯度
(就是我们现在用的)
随着机器学习技术的发展,数据规模的逐渐扩大,单机进行机器学习训练时,资源渐渐显得捉襟见肘。即使我们可以提供TB级别的计算机,但计算机硬件资源的增长速度往往难以追赶上数据量的增加速度,这时候,单纯扩大单机的资源很难满足当前和未来的发展,多机分布式计算迫在眉睫。
数据并行、模型并行与计算并行
数据并行是将数据分为多份,每个节点处理其中一份数据;模型并行是将模型拆分成多个组件,每个节点处理一部分模型的计算。相比来说,数据并行的实现比较简单,而模型并行的实现较为复杂,除非模型的规模特别大,否则采用数据并行会更加容易。而计算并行则是既不拆分模型,也不拆分数据,而是多个计算节点之间共享内存,共同分担计算任务,实现更为复杂。
随机梯度下降算法可以放置于多个计算节点中,每个节点先获取最新的模型参数,然后读取一小批训练数据集,计算这一批数据的梯度。之后,每个节点与其他节点通信,传递梯度值,并更新全局模型参数,循环往复,直到迭代停止。
同步算法与异步算法
当每个节点计算出梯度值时,就需要与其他节点通信,以更新模型参数。由于不同节点的计算速度存在或多或少的差异,这时候存在一个问题,即是否需要等待全部节点计算完毕再更新模型的参数。如果不同计算节点的速度差异不太大,那么同步算法是一个不错的选择,但如果差异过大,那么实际速度取决于最慢节点,会导致整个集群的计算速度大幅降低,影响性能,这时候最好采用异步算法实现。
对于异步的算法来说,需要专门指定一个节点为主节点,作为参数服务器。某个子节点将计算后的梯度交给主节点,由主节点直接加到全局模型上,进行参数更新,无需等待其他子节点的梯度信息。不过,异步算法会导致梯度更新出现延迟,当一个节点计算完梯度后,模型可能已经是更新后的版本,这时梯度与模型会出现失配的问题,可能导致模型在特定更新点上出现严重抖动,甚至优化过程出错,最终无法收敛。
综上,同步梯度下降与异步梯度下降是建立在分布式计算基础上的算法。
5.5.4 DNN中术语解释
backbone
一个网络的主干部分,这个主干网络大多时候指的是提取特征的网络。比如在图像分类任务中。这些网络经常使用的是resnet VGG等,而不是我们自己设计的网络,因为这些网络已经证明了在分类等问题上的特征提取能力是很强的。在用这些网络作为backbone的时候,都是直接加载官方已经训练好的模型参数,后面接着我们自己的网络。让网络的这两个部分同时进行训练,因为加载的backbone模型已经具有提取特征的能力了,在我们的训练过程中,会对他进行微调,使得其更适合于我们自己的任务。
head
head是获取网络输出内容的网络,利用之前提取的特征,head利用这些特征,做出预测。
neck
是放在backbone和head之间的,是为了更好的利用backbone提取的特征
bottleneck
瓶颈的意思,通常指的是网网络输入的数据维度和输出的维度不同,输出的维度比输入的小了许多,就像脖子一样,变细了。经常设置的参数 bottle_num=256,指的是网络输出的数据的维度是256 ,可是输入进来的可能是1024维度的。
GAP
Global Average Pool全局平均池化,就是将某个通道的特征取平均值
Embedding
深度学习方法都是利用使用线性和非线性转换对复杂的数据进行自动特征抽取,并将特征表示为“向量”(vector),这一过程一般也称为“嵌入”
pretext task & downstream task
用于预训练的任务被称为前置/代理任务; 用于微调的任务被称为下游任务
warm up
指的是用一个小的学习率先训练几个epoch,这是因为网络的参数是随机初始化的,一开始就采用较大的学习率容易数值不稳定。
end to end
给了一个输入,我们就给出一个输出,不管其中的过程多么复杂,但只要给了一个输入,就会对应一个输出。比如分类问题,你输入了一张图片,不管网络内部如何变化,都会输出一个预测结果,算法细节和学习过程全部丢给了神经网络。
5.5.5 label smoothing
Label Smoothing(标签平滑),如 L1、L2 和 Dropout 一样,是一种正则化方法,通常用于分类问题,目的是防止模型在训练时过于自信地预测标签,改善泛化能力差的问题(也是解决错误标注的一种方法)。
label smoothing 公式如下:
y’i 表示在原标签基础上修改后的标签值,yi 为原标签值。以二分类为例,原标签值为[0,1],经过计算之后,标签值就变为了[0.05,0.95]。简单来说就是把 label 给重置了一下。
5.5.6 weight decay
weight decay,即权重衰减,也叫 L2 正则化,可以减少模型过拟合问题。
L2 正则化就是在代价函数后再加上一个正则化项:
其中C0代表原始的代价函数,后面那一项就是L2正则化项,它是这样来的:所有参数w的平方的和,除以训练集的样本大小n。λ 就是正则项系数,也叫做权重衰减系数,用来权衡正则项与C0项的比重。另外还有一个系数1/2,1/2 经常会看到,主要是为了后面求导的结果方便,后面那一项求导会产生一个2,与1/2相乘刚好凑整为1。
我们对 L2 正则化后的函数求导,得
可见 L2 正则化项对于偏置 b 的更新没有影响,对于权重 w 的更新有影响。
在不使用L2正则化时,求导结果中 w 前系数为1,现在 w 前面系数为1-ηλ/n,因为 η、λ、n 都是正的,所以 1-ηλ/n 小于1,它的效果是减小 w,这也就是权重衰减(weight decay)的由来。
对于基于 mini-batch 的随机梯度下降来说,w 和 b 的更新公式不同了:
其中,m 是一个 mini-batch 中样本的个数
原理:
- 从模型的复杂度上解释:更小的权值w,从某种意义上说,表示网络的复杂度更低,对数据的拟合更好(这个法则也叫做奥卡姆剃刀),而在实际应用中,也验证了这一点,L2正则化的效果往往好于未经正则化的效果。
- 从数学方面的解释:过拟合的时候,拟合函数的系数往往非常大,过拟合,就是拟合函数需要顾忌每一个点,最终形成的拟合函数波动很大。在某些很小的区间里,函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值(绝对值)非常大,由于自变量值可大可小,所以只有系数足够大,才能保证导数值很大。而正则化是通过约束参数的范数使其不要太大,所以可以在一定程度上减少过拟合情况。
5.6 超参数 α 和 ρ
这两个超参数的引进都是为了减小模型的尺寸和计算成本,让模型在原有基础上变得 smaller and faster
简单地说,α 减小每一层的输入输出通道数;ρ 减小输入图像的spatial dimensions
5.6.1 Width Multiplier α
α 的目的
使网络在每一层上均匀的变“薄”
加上 α 后,输入通道数 M 变成 αM, 输出通道数 N 变成 αN(当然,α大于0且小于等于1),那么每一层的计算成本就变成了:
α 的典型取值有 1,0.75,0.5 以及 0.25
我们将原版网络的计算成本与加上 α 的网络的计算成本一对比,可以看出减少的计算成本大概在 α 的平方级别。
α 这个超参数不仅可以在 MobileNet 中用,还可以在其他任何网络结构中用(除非不是CNN的这种卷积计算模式)
5.6.2 Resolution Multiplier ρ
ρ 是用来减小输入图像的分辨率的,即缩小输入图像的 spatial dimensions
加入 ρ 后的计算成本如下:
同样的,ρ 的值也是大于0且小于等于1,与 α 不同的是,我们通常不直接定义 ρ 的值,而是通过定义输入图像的分辨率(边长)来隐性地定义 ρ。典型的分辨率有 224,192,160 以及 128。
ρ 的加入又可以将计算成本减小 ρ 的平方级别
6 数据图解析
加上 α 和 ρ 后的计算量和参数变化
每一行的结果都是以上一行为基础作的变化,比如第二行是将标准卷积改为深度可分离卷积的结果,第三行是在深度可分离卷积的基础上加上 α 的结果,第四行是在第三行的基础上加上 ρ 后的结果。
注意 Mult-Adds 是乘加次数,以计算成本只考虑乘法不一样
各种 MobileNet 大比拼
以下对比都是三个方面:在ImageNet上的精确度、乘加次数以及参数个数
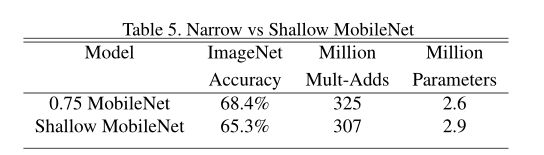
Table 5 说的 shallow 指的是减少层数(将原MobileNet中的 5 层 14·14·512 的深度可分离卷积去除了)
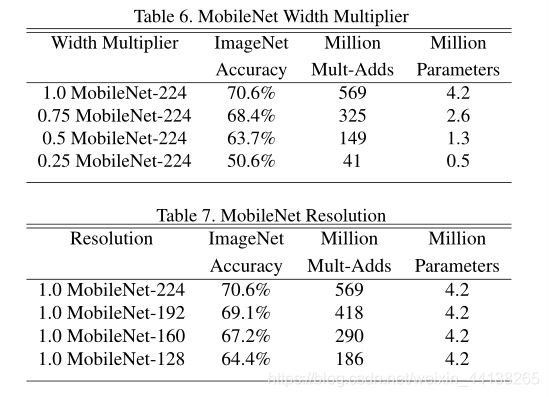
Table 6 比较了 ρ 相同时,α 对模型的影响;Table 7 比较了 α 相同时,ρ对模型的影响。
在 “1.0 MobileNet-224”这个表述中,1.0 指的是 α 的值,224 反映的是 ρ 的值(隐性)
注意,参数个数只与卷积核有关,与输入无关。ρ 改变的只是输入图像,因此无论 ρ 如何变化都不会影响参数个数
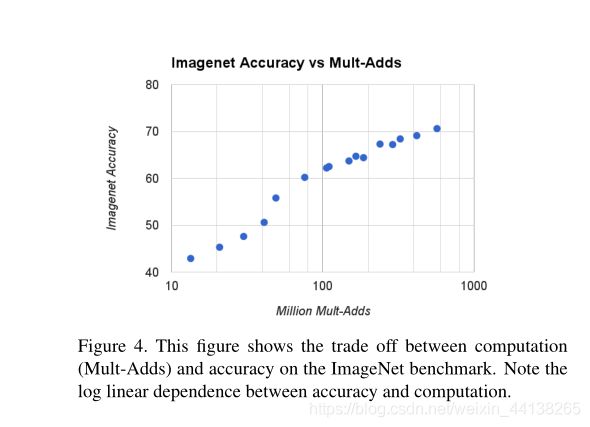
接下来,我们取 α 为 1,0.75,0.5,0.25;取 ρ 为224,192,160,128,令这它们分别两两配对形成16个组合,由此产生16个模型以及16组ImageNet Accuracy 、Million Mult-Adds、Million Parameters,将16个点以
ImageNet Accuracy = lg(Million Mult-Adds) 以及
ImageNet Accuracy = lg(Million Parameters)
的对数关系分别画在坐标图上,可见:
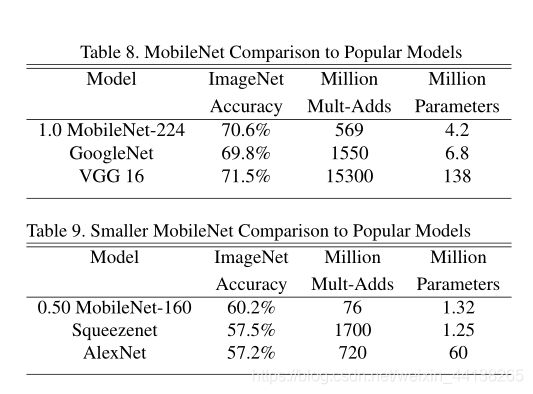
MobileNet 与其他网络结构大比拼
可以看到,MobileNet 在精度相等甚至更高时 ,在计算量和尺寸方面相比其他经典网络是有明显的优势的
7 知识点补充
7.1 什么叫蒸馏
蒸馏神经网络到底在蒸馏什么?(设计思想篇)
关键词:迁移学习 softmax T值
- 首先用较大的T值来训练模型,这时候复杂的神经网络能够产生更均匀分布的软目标;
- 之后小规模的神经网络用相同的T值来学习由大规模神经产生的软目标,接近这个软目标从而学习到数据的结构分布特征;
- 最后在实际应用中,将T值恢复到1,让类别概率偏向正确类别