传统机器学习笔记3——逻辑回归算法

前言

  上篇博文我们介绍了KNN算法，这篇博文我们继续开始我们的传统机器学习之旅，开始学习逻辑回归算法。逻辑回归是目前工业界解决问题最常用的算法，因为他简单有效并且可解释性强。接下来主要从以几个方介绍下逻辑回归算法：核心思想、sigmoid函数与分类器决策边界、模型优化使用的梯度下降算法、模型过拟合问题的正则化、特征变换与线性切分。

一.逻辑回归核心思想

  逻辑回归也是线性回归，他是线性回归的一种扩展，关于什么是线性模型，什么是非线性模型，可以看如下图的解释。

1.1.线性回归与分类

  其实回归和分类没多大的差别，都是通过岁已有数据的学习来对新数据预测，只不过分类输出的是离散值，回归输出的是连续值。这里引出一个问题，我们能不能在回归的基础上进行分类？其中一个思路是先用线性拟合，然后对结果进行量化，这样就可以使用：线性回归+阈值来解决分类问题了。逻辑回归正是借助了这种思想。如下图所示，假设我们有一组学学生的成绩，大于60分就判定为及格，否者不及格，学生的成绩拟合出来的曲线如下图所示：

  我们以y=60为分界线，大于60的判定为及格，就输出1。小于60的判定为不及格，输出0。这样是不是就完成了分类了。但是呢这个时候会有一个问题，单纯的讲线性拟合的输出值域某个阈值进行比较，将会导致分类很不稳定，即我们的数据稍微变一下有些数据的分类就不对了。

1.2.核心思想

  上面讲了简单的线性回归+阈值很难得到鲁棒性好的分类器，所以我们现在要做的就是怎么对其改进得到一个鲁棒性比较好的逻辑回归模型。如果线性回归的结果输出的是一个连续的值，并且值的范围无法限定，这个时候我们就没法得到稳定二维判定阈值，如果把这个结果映射成一个区间呢，比如类似归一化这种操作后再进行判断。这就是我们的逻辑回归要做的事情，其中对连续数值进行压缩变换的函数就是大名鼎鼎的Sigmoid函数，也是我们常说的logistic函数。
$$S(x)=\frac{1}{1+e^{-x}}$$

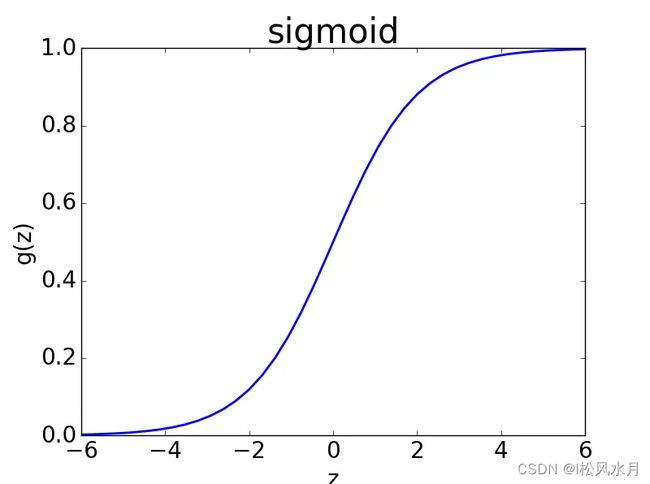
  从上面的图可以看到Sigmoid函数的输出值在(0,1)之间。如果线性回归的输出结果是一个连续的值，并且值的范围无法限定，我们就可以把这个结果映射为(0,1)上的概率值。

二.Sigmoid函数与决策边界

  决策边界就是分类器对样本进行区分的边界，有线性和非线性的。

2.1.线性决策边界的生成

  我们怎么才能得到线性决策边界，他跟sigmoid函数有什么联系？假设我们有一个线性分类函数$y=x_1+x_2-3$，将其代入逻辑回归函数$S(x)=\frac{1}{1+e^{-x}}$，假设有一个点是(10,10)代入y之后再计算sigmoid函数可得sigmoid大于0.5，因此将其映射为1。如果是(0,0)代入sigmoid函数，则sigmoid函数小于0.5，因此将其映射为0。我们刚才讲的都是以0(横轴)为边界，如果以0.5位边间呢，那么决策边界就换成了另一条线了。所以结果往往跟我们设定的决策线有关，但是趋势任然不变。

2.2.非线性决策边界生成

  入过上面的$y=x_1+x_2-3$改为一个非线性函数，如二元函数，椭圆函数等非线性函数，那么这个时候我们可以得到对样本进行非线性切分的非线性决策边界，这里的非线性指的是无法通过直线或者超平面把不同类别的样本很好地切分开。如我们现在假定$x_1^2+x_2^2=4$，也就是说这个时候决策边界变成了一个非线性的，同样代入上面的两组数据，代入(10,10)的时候在圆外取值大于0，经过sigmoid函数之后取值大于0.5，映射为1，代入(0,0)的时候取值在圆内
取值小于0，映射为0。同样，如果我们把判定边界换成0.5则决策边界又换成了另一条决策线了。

三.梯度下降与优化

3.1.损失函数

  上面我们都是手动设置的函数得到决策边界，代入sigmoi函数得到判定结果。但是会有一个严重的问题，我们上面也提到了，就是我们对决策函数参数取不同的值会得到不同的决策边界。我们应该怎么确定决策边界，到底哪个决策边界好呢？这个时候就要用到损失函数了，损失函数就是我们用来判断模型好坏的函数，我们的目标就是让损失函数尽可能的小，从而找到一个最优的决策边界。那么我们用该如何来定义损失函数呢，也就是说我们应该如何来衡量预测值和实际值的误差。我们前面讲过几种误差函数，首先能想到的就是均方误差，为啥选他呢，因为他简单呀，在看下他的定义，是不是很简单。
$$MSE=\frac{1}{m}\sum _{i=1}^m{\left(f\left(x_i\right)-y_i\right)}^2$$
  我们现在的目的就是让这个值越小越好，越小说明预测值和实际值之间差距越小。有一点需要注意的是，MSE在回归问题中比较适用，但是在逻辑回归中就有点不太适合了。因为在逻辑回归场景下，Sigmoid 函数的变换使得我们最终得到损失函数曲线如下图所示，是非常不光滑凹凸不平的，是非凸函数，数学特性不太好，而我们希望得到的是凸函数。在凸优化中，局部最优解也是全局最优解，这个特性使得凸优化问题在一定意义上更易于解决，而一般的非凸最优化问题相比之下更难解决。如下图左边是非凸函数，右边是凸函数，是不是看着凸函数友好多了。当使用均方误差计算的时，函数如下：
$$J(\theta )=\frac{1}{m}\sum _{i=1}^m\frac{1}{2}{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$$
其中$h_{\theta }(x^{(i)})$是经过sigmoid计算后的值，$y^{(i)}$是真实值，可以假设$h_{\theta }(x^{(i)})$为如下表达式，$\theta$就是决策函数的参数。
$$h_{\theta }(x)=g\left({\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_1^2+{\theta }_4{x}_2^2\right)$$

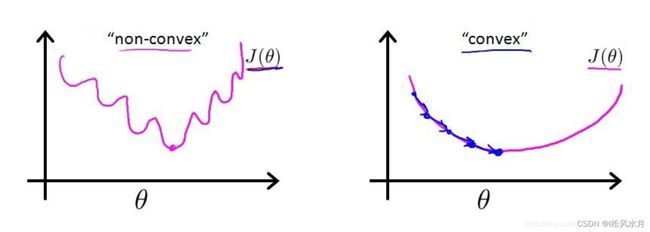
  那么我们有什么方法能够得到右边的函数图像呢，需要用到凸优化理论，有点复杂。于是我们换了一个思路，有没有另外的损失函数计算出来就是就是凸函数，从而引申出了对数损失函数，也就是我们常说的二元交叉熵损失函数，他既可以保证损失函数的凸函数特性，又可以很好的衡量模型性能的好坏，岂不美哉。二元交叉熵损失函数如下：
$$J(\theta )=-\frac{1}{m}\left[\sum _{i=1}^m{y}^{(i)}\log h_{\theta }\left(x^{(i)}\right)+\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)\right]$$
其中，$y^{(i)}$表示样本取值，正样本时为1，负样本的时候取值为0。我们来看下这两种情况

  观察上面的函数曲线，左边为$y^{(i)}$取值为1的时候，也就是正样本的时候。右边为$y^{(i)}$取值为0的时候，也就是取值为负样本的时候。

• $y^{(i)}$=1：当一个样本为正样本时，若$Y_{pred}$的结果接近0（即预测为负样本），那么$-log(Y_{pred})$的值很大，那么得到的惩罚就大。
• $y^{(i)}$=0：当一个样本为负样本时，若$Y_{pred}$的结果接近1（即预测为正样本），那么$-log(1-Y_{pred})$的值很大，那么得到的惩罚就大。

  简言之，预测值跟实际值之间差距越大，惩罚越大，损失越大，不能背道而驰。

3.2.梯度下降

  上面我们确定了损失函数，但是我们任然会遇到一个问题，就是怎么找到这个损失函数的最小值。于是有引入了梯度下降算法，其实还有很多其他的算法，只不过梯度下降使我们使用频率最高的，如下图所示：

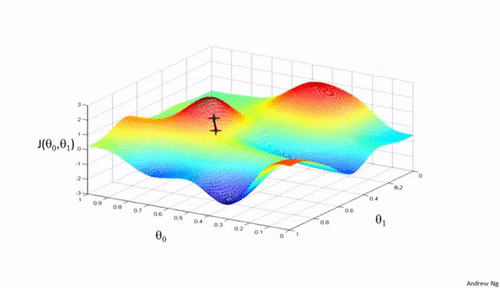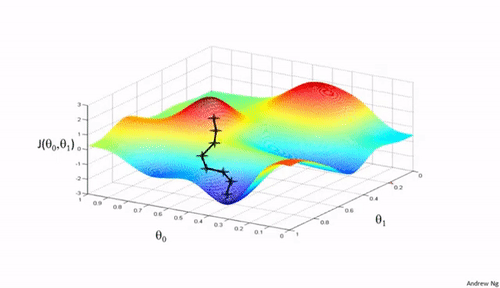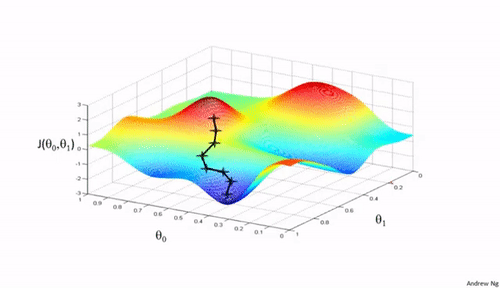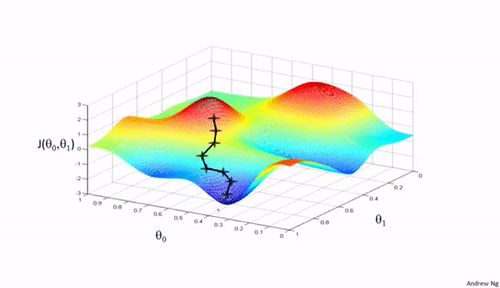
  梯度下降算法，是一个一阶最优化算法，通常也称为最速下降法。要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索。

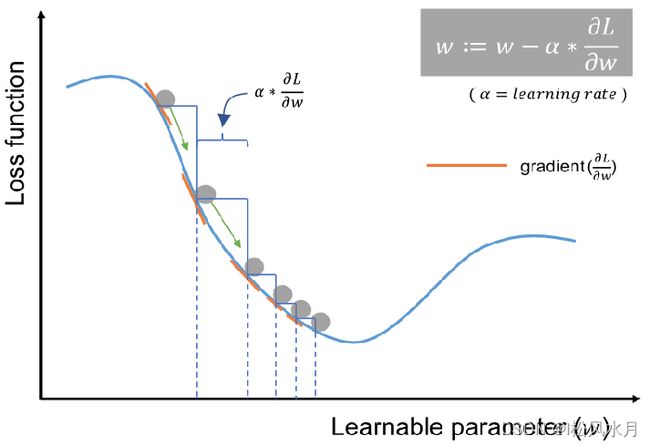
  上图中的$\alpha$就是我们每次更新梯度的步进大小，又称为学习率，太大一般会错过极小值，太小会导致迭代次数过多。

四.正则化与过拟合

  上面介绍了损失函数和梯度下降，下面我们再来看下正则化。

4.1.过拟合

  我们知道，当我们的训练数据不多时，而我们的模型又比较复杂的时候，这个时候模型是很容易出现过拟合现象的，所谓的过拟合就是我们的模型把这些训练数据的所有特征都学会了，当我们输入一组新的数据给他时，如果新的数据的特性跟训练数据集差距比较大的时候预测的结果就会很差。有过拟合就会有欠拟合，欠拟合就是模型训练的不够，或者说模型复杂度低，数据量相比较于模型而言，模型很难把给定的训练数据特征充分学习。从过拟合，欠拟合又衍生出来了泛化性能，所谓的泛化性是指机器学习算法对新鲜样本的适应能力。学习的目的是学到隐含在数据背后的规律，对具有同一规律的学习集以外的数据，经过训练的网络也能给出合适的输出，该能力称为泛化能力。

4.2.正则化

  上面我们讲了过拟合，那么有没有什么方法能够解决过拟合，或者缓解或拟合现象呢？通常有两个解决方法，其中一个是增加数据，但是，我们知道数据有时候并不好获取，于是就出现了正则化，我们通过对损失函数添加正则项来约束参数的搜索空间，从而保证拟合的决策边界并不会抖动的非常厉害。如下式子为二元交叉熵损失函数加上了一个L2正则化。
$$J(\theta )=\frac{1}{m}\sum _{i=1}^m\left[-y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)\right]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$
其中，$\lambda$为正则化系数，表示惩罚程度。$\lambda$的值越大，为了使$J(\theta )$的值越小，参数$\theta$的值就越小，通常对应于越光滑的函数，即更加简单的函数，因此不容易发生过拟合。

五.特征变换与非线性表达

5.1.多项式特征

  对于输入的特征，如果我们直接进行线性拟合后再给到 Sigmoid 函数，得到的是线性决策边界。如果添加多项式特征，可以对样本点进行多项式回归拟合，也能在后续得到更好的非线性决策边界。
  多项式回归，回归函数是回归变量多项式。多项式回归模型是线性回归模型的一种，此时回归函数关于回归系数是线性的。
  在实际应用中，通过增加一些输入数据的非线性特征来增加模型的复杂度通常是有效的。一个简单通用的办法是使用多项式特征，这可以获得特征的更高维度和互相间关系的项，进而获得更好的实验结果。

5.2.非线性切分

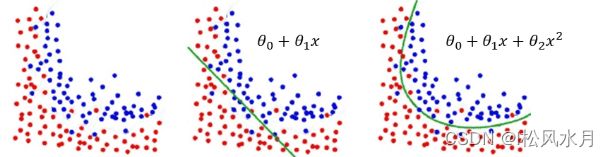
  在逻辑回归中，拟合得到的决策边界，可以通过添加多项式特征，调整为非线性决策边界，具备非线性切分能力。

• 中$Z_{\theta }(x)$是参数，当$Z_{\theta }(x)={\theta }_0+{\theta }_{1}x$时，此时得到的是线性决策边界；
• $Z_{\theta }(x)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2$ 时，使用了多项式特征，得到的是非线性决策边界。

  目的是低维线性不可分的数据转化到高维时，会变成线性可分。得到在高维空间下的线性分割参数映射回低维空间，形式上表现为低维的非线性切分。

  以上就是关于逻辑回归算法的介绍，欢迎各位大佬批评指正。